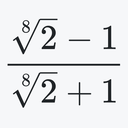自己紹介

$\beginend{align}{ \frac{\sqrt[8]2-1}{\sqrt[8]2+1} &= \Kfrac_{n=0}^\infty \frac1{2\sinh((2n+1)\pi)} \\ \tan\frac\pi{48} &= \Kfrac_{n=0}^\infty \frac1{2\cosh\frac{(2n+1)\pi\sqrt3}2} \\ \frac1{\sqrt[4]2} &= \Kfrac_{n=0}^\infty \frac{\cosh^2\!\frac{n\pi}4}{\sinh\frac{(2n+1)\pi}4} \\ \frac{\sqrt[4]2-1}{\sqrt[4]2+1} &= \Kfrac_{n=0}^\infty \frac{\cosh^2(n\pi)}{\sinh((2n+1)\pi)} \\ \sqrt{\frac{\sqrt2-1}2} &= \frac12\Kfrac_{n=0}^\infty \frac{2\cosh\frac{n\pi}2}{2\sinh\frac{(2n+1)\pi}4} \\ \color{var(--bs-danger)}\frac\varpi{2\pi} &\;\color{var(--bs-danger)}= \Kfrac_{n=0}^\infty \frac{\sinh^2\!\frac{n\pi}2+\delta_{n,0}}{\sinh\frac{(2n+1)\pi}2} }$

任意の基数において、
$\displaystyle{ \frac{1}{1}+\frac{z^1}{111}+\frac{z^{1+1}}{11111}+ \frac{z^{1+1+1}}{1111111}+\cdots = \cfrac{1} {1-\cfrac{1^{1+1}1z} {111-\cfrac{11^{1+1}10z} {11111-\cfrac{111^{1+1}100z} {1111111-\ddots}}}} }$

$\beginend{eqnarray}{ \sigma(n) &=& \sum_{k\in\Z\setminus\{0\}} (-1)^{k-1}\lr({\sigma\lr({n-\frac{k(3k-1)}{2}}) + \delta_{n,k(3k-1)/2}n}) \\ &=& \sum_{k\ge1} (-1)^{k-1}(2k+1)\lr({\sigma\lr({n-\binom{k+1}{2}}) + \delta_{n,\binom{k+1}{2}}\frac{n}{3}}) }$
ただし、$\sigma(n) = 0 \ (n\le0)$。
1行目はオイラーによって発見されています。

$\large\displaystyle \frac{\sum_{n=1}^\infty\frac{(-1)^{n-1}\ln(2n+1)}{\sqrt{2n+1}}}{\sum_{n=0}^\infty\frac{(-1)^n}{\sqrt{2n+1}}} = \frac{\gamma+\ln(2\pi)}2-\frac\pi4$

$\large \hygeo3F2{a,b,-n}{\frac{a+b}2,\frac{a+b+1}2}{1} = \hygeo2F1{a,-2n}{a+b}{2} $

$\beginend{alignat}{2 &\zeta{\qty(\{s\}^m)} &&= \sum_{j=1}^m (-1)^{m-j} &&\sum_{0=\Range k0j<=m} \prod_{l=1}^j \frac{\zeta((k_l-k_{l-1})s)}{k_l} \\ &\zeta^\star{\qty(\{s\}^m)} &&= \sum_{j=1}^m &&\sum_{0=\Range k0j<=m} \prod_{l=1}^j \frac{\zeta((k_l-k_{l-1})s)}{k_l} }$

$\large p\in\P$
$\large\displaystyle \binom{ap}{bp}\equiv\binom ab\pmod p$

$\beginend{align}{ \pi &= \cfrac4 {1+\cfrac1 {3+\cfrac{1+3} {5+\cfrac{1+3+5} {7+\quad{\scriptsize\ddots}}}}} \\ \varpi &= \cfrac2 {1-\cfrac1 {5-\cfrac{1+5} {9-\cfrac{1+5+9} {13-\quad{\scriptsize\ddots}}}}} }$