1-1/3+1/5-1/7+…=π/4の視覚化
はじめに
この記事では、先日私が X(旧Twitter) にポストした次の画像について解説します。
1/tan(π/4)=1
— apu (@apu_yokai) December 15, 2023
ゆえに
1-1/3+1/5-1/7±…=π/4
の図 pic.twitter.com/VAgqxqpYZN
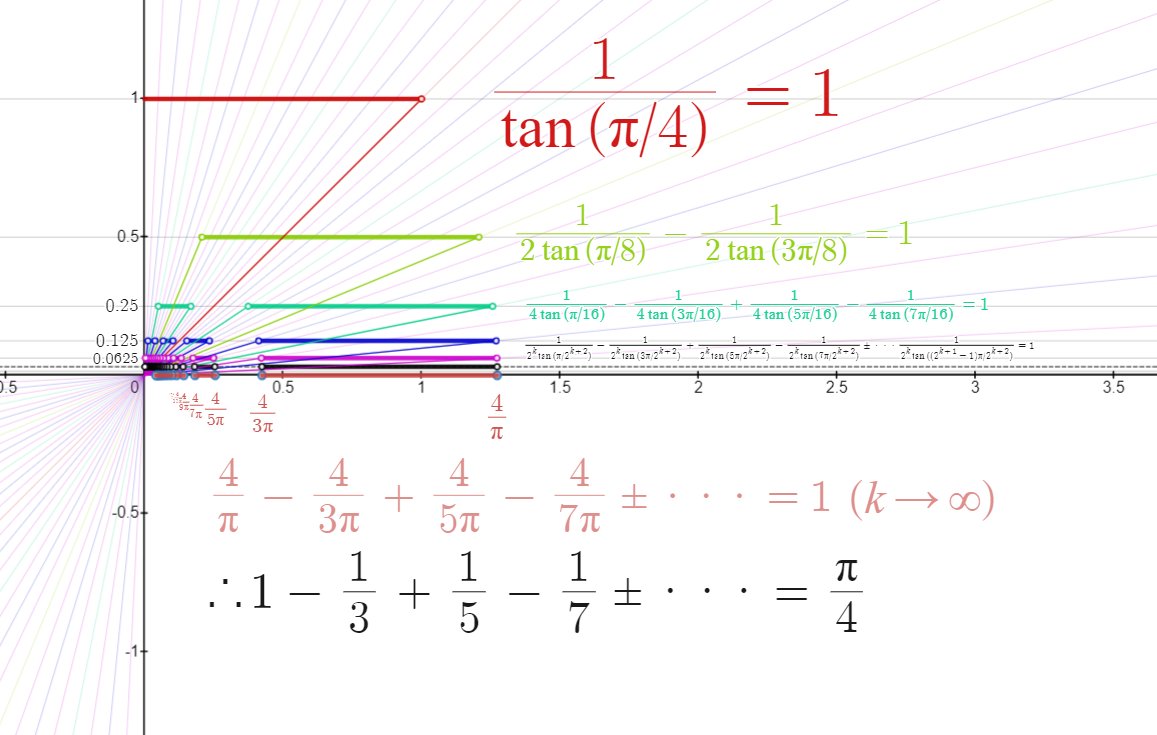 1-1/3+1/5-1/7+…=π/4の視覚化
1-1/3+1/5-1/7+…=π/4の視覚化
この図を作ったモチベーション
みなさんはグレゴリー・ライプニッツ級数とかライプニッツの公式と呼ばれる次の式をご存じでしょうか?
${\displaystyle 1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}\pm\cdots=\frac{\pi}{4}}$
規則的に分数を足したり引いたりするだけの簡単な式で円周率を計算できるという、初見では信じがたい形をした級数です。
私は中学生のときに初めてこの式を見て衝撃を受けました。「こんな簡単な式で円周率が計算できるわけないやん!」と・・・
覚えたばかりのBASICで計算してみて、確かに $3.14\cdots$ に収束しそうなのを見て「ほんまや・・・」となってから、私はこの級数が大好きです。
ただし、世間での扱いはそれほどではないように思います。その理由は私の想像では、収束の遅さがハンパないからではないかと思います。
例えば第 $100$ 万項あたりまで計算しても、誤差約 $200$ 万分の $1$ の幅で上下にフラフラしてるわけですから、桁数としては小数点以下 $6$ ケタがやっと。
そのことは、式の形をみればなんとなくわかると思います。
この収束の遅さ、他のいろいろな円周率公式と比べても圧倒的に遅い。
しかし、収束の遅さを差し引いても、この見た目の美しさは最高だと思います。「出来の悪い子ほどカワイイ」みたいなものかもしれませんが。
ともかく、私はこの式の「見た目」が好きなのです。しかし、世に広まっているこの式の「証明」は、この「見た目」とあまりにかけ離れているものばかりだと感じていました。「もっと視覚的に納得したい!」と。「$\frac{1}{3}$ は $\frac{1}{3}$ のままで、$\frac{1}{5}$ は $\frac{1}{5}$ のままで直接この式を感じたい!」と。
というわけで作ってみたのが先の図というわけでした。
先の図では、「$\frac{1}{\tan(\pi/4)}=1$」から始めて、項をどんどん $2$ つずつに「分割」していき、分割を繰り返した極限から $\frac{1}{3}$ や $\frac{1}{5}$ が現れ、ライプニッツの公式に至る様子を視覚化しています。
ざっくり導出
それではここから、どのようにして「$\frac{1}{\tan(\pi/4)}=1$」からライプニッツの公式を導出したのか説明します。
まず、$\tan$ についての次の補題を見てください。
${\displaystyle \tan(\theta)=\frac{1}{\tan\left(\frac{\pi}{2}-\theta\right)} }$
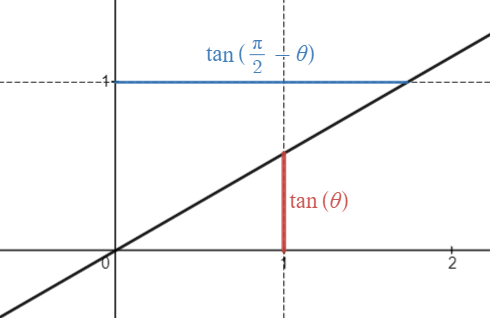 tanの関係
tanの関係
${\displaystyle \begin{align} \tan(\theta) =\frac{\sin(\theta)}{\cos(\theta)} =\frac{\cos(\pi/2-\theta)}{\sin(\pi/2-\theta)} =\frac{1}{\tan\left(\frac{\pi}{2}-\theta\right)} \end{align} }$
補題 $1$ を使って次の補題 $2$ を示します。
${\displaystyle \frac{1}{\tan(2\theta)}=\frac{1}{2\tan(\theta)}-\frac{1}{2\tan(\pi/2-\theta)} }$
${\displaystyle \begin{align} \frac{1}{\tan(2\theta)} &=\frac{\cos(2\theta)}{\sin(2\theta)}\\ &=\frac{\cos^2(\theta)-\sin^2(\theta)}{2\sin(\theta)\cos(\theta)}\\ &=\frac{\cos(\theta)}{2\sin(\theta)}-\frac{\sin(\theta)}{2\cos(\theta)}\\ &=\frac{1}{2\tan(\theta)}-\frac{\tan(\theta)}{2}\\ &=\frac{1}{2\tan(\theta)}-\frac{1}{2\tan(\pi/2-\theta)} \end{align} }$
補題 $2$ を使って、${\displaystyle \frac{1}{\tan(\pi/4)}}$ を「分割」します。
${\displaystyle \begin{align} 1 &=\frac{1}{\tan(\pi/4)}\\ &=\frac{1}{2\tan(\pi/8)}-\frac{1}{2\tan(3\pi/8)}\\ \end{align} }$
もう一回「分割」すると
${\displaystyle \begin{align} &\frac{1}{2\tan(\pi/8)}-\frac{1}{2\tan(3\pi/8)}\\ &\left(=\left(\frac{1}{2^2\tan(\pi/16)}-\frac{1}{2^2\tan(7\pi/16)}\right)-\left(\frac{1}{2^2\tan(3\pi/16)}-\frac{1}{2^2\tan(5\pi/16)}\right)\right)\\ &=\frac{1}{2^2\tan(\pi/16)}-\frac{1}{2^2\tan(3\pi/16)}+\frac{1}{2^2\tan(5\pi/16)}-\frac{1}{2^2\tan(7\pi/16)}\\ \end{align} }$
こうなります。
分割するたびに項数が $2$ 倍になり、分母の数が規則的に大きくなっていることがわかります。
このように次々と「分割」することで、次々と新しい式が得られます。
どの式も値は $1$ であることに注意してください。
${\displaystyle \frac{1}{\tan(\pi/4)}=1 }$
${\displaystyle \frac{1}{2\tan(\pi/8)}-\frac{1}{2\tan(3\pi/8)}=1 }$
${\displaystyle \frac{1}{2^2\tan(\pi/16)}-\frac{1}{2^2\tan(3\pi/16)}+\frac{1}{2^2\tan(5\pi/16)}-\frac{1}{2^2\tan(7\pi/16)}=1 }$
$\qquad\vdots$
${\displaystyle \frac{1}{2^k\tan(\pi/2^{k+2})}-\frac{1}{2^k\tan(3\pi/2^{k+2})}\pm\cdots-\frac{1}{2^k\tan((2^{k+1}-1)\pi/2^{k+2})}=1 }$
このような「分割」が常に可能であることを式で確認しておきましょう。
$k$ を非負整数とし、
${\displaystyle I_k=\sum_{n=1}^{2^{k}} \frac{(-1)^{n+1}}{2^k\tan((2n-1)\pi/2^{k+2})} }$
とします。$I_k=1$ の左辺を「分割」して $I_{k+1}=1$ の式が得られることを確認します。
${\displaystyle \begin{align} I_k&=\sum_{n=1}^{2^{k}} \frac{(-1)^{n+1}}{2^k\tan((2n-1)\pi/2^{k+2})}\\ &=\sum_{n=1}^{2^{k}} \left( \frac{(-1)^{n+1}}{2^{k+1}\tan((2n-1)\pi/2^{k+3})} -\frac{(-1)^{n+1}}{2^{k+1}\tan((2^{k+2}-(2n-1))\pi/2^{k+3})} \right)\\ &=\sum_{n=1}^{2^{k}} \frac{(-1)^{n+1}}{2^{k+1}\tan((2n-1)\pi/2^{k+3})} -\sum_{n=2^{k}+1}^{2^{k+1}} \frac{-(-1)^{n+1}}{2^{k+1}\tan((2n-1)\pi/2^{k+3})} \\ &=\sum_{n=1}^{2^{k+1}} \frac{(-1)^{n+1}}{2^{k+1}\tan((2n-1)\pi/2^{k+3})}\\ &=I_{k+1} \end{align} }$
と変形できますので、この「分割」は何回でも繰り返すことができることが確認できました。
さて、この分割を繰り返していくと、各項が特定の値へと収束していきます。収束先を式で確認してみましょう。$I_k$ の第 $n$ 項を $a_{k,n}$ とすると
${\displaystyle a_{k,n}=\frac{(-1)^{n+1}}{2^k\tan((2n-1)\pi/2^{k+2})}}$
で表すことができます。
※ $n \gt 2^k$ のときは項が存在しませんが、ここでは $k\to\infty$ の極限を考えているので気にしないことにします。
${\displaystyle\lim_{x\to0}\frac{x}{\tan x}=1}$ を使って変形すると
${\displaystyle \begin{align} \lim_{k\to\infty}a_{k,n} &=\lim_{k\to\infty} \frac{(-1)^{n+1}}{2^k\tan((2n-1)\pi/2^{k+2})}\\ &=\lim_{k\to\infty} \frac{2^{k+2}}{(2n-1)\pi}\cdot\frac{(-1)^{n+1}(2n-1)\pi/2^{k+2}}{2^k\tan((2n-1)\pi/2^{k+2})}\\ &=\frac{(-1)^{n+1}\cdot 2^2}{(2n-1)\pi}\cdot1\\ &=\frac{(-1)^{n+1}\cdot 4}{(2n-1)\pi}\\ \end{align} }$
となりました。したがって、$I_k$ の収束先を具体的に書き下すと
${\displaystyle\frac{4}{\pi}-\frac{4}{3\pi}+\frac{4}{5\pi}-\frac{4}{7\pi}\pm\cdots}$
となります。$I_k=1$ と合わせて次の式が得られました。
${\displaystyle\frac{4}{\pi}-\frac{4}{3\pi}+\frac{4}{5\pi}-\frac{4}{7\pi}\pm\cdots=1}$
両辺に $\dfrac{\pi}{4}$ を乗じることで所望の式が得られました!
${\displaystyle 1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}\pm\cdots=\frac{\pi}{4}}$
もう少し厳密に
ここまでの議論がなんだか厳密でなさそうでだまされてる気がする、と感じる人のためにもう少し厳密にこの式をみていくことにしましょう。
${\displaystyle I_k=\sum_{n=1}^{2^{k}} \frac{(-1)^{n+1}}{2^k\tan((2n-1)\pi/2^{k+2})} }$
の両辺を $\dfrac{\pi}{4}$ 倍したものを $I'_k$ とします。
${\displaystyle I'_k=\sum_{n=1}^{2^{k}} \frac{(-1)^{n+1}\cdot\pi}{2^{k+2}\tan((2n-1)\pi/2^{k+2})} }$
このとき、$k$ にかかわらず必ず $I_k=1$ ですから、必ず $I'_k=\dfrac{\pi}{4}$ となることに注意します。
つぎに、ライプニッツの公式の第 $2^k$ 項までの部分和を $J_k$ とします。
${\displaystyle J_k=\sum_{n=1}^{2^{k}} \frac{(-1)^{n+1}}{2n-1} }$
このとき、$\lim_{k\to\infty}(I'_k-J_k)=0$ となることを式で確認しましょう。
まず、積分を使うことで、誤差項を評価することを考えます。$k>0$ のとき
${\displaystyle \begin{align} \frac{\pi}{4} &=\int_0^{\pi/4}\tan^0x\,dx\\ &=\int_0^{\pi/4}\tan^0x\cdot\frac{dx}{\cos^2 x}-\int_0^{\pi/4}\left(\frac{1}{\cos^2 x}-1\right)\tan^0x\,dx\\ &=\int_0^{1}u^0\,du-\int_0^{\pi/4}\tan^2x\,dx\\ &=1-\int_0^{\pi/4}\tan^2x\,dx\\ &=1-\left(\int_0^{\pi/4}\tan^2x\cdot\frac{dx}{\cos^2 x}-\int_0^{\pi/4}\left(\frac{1}{\cos^2 x}-1\right)\tan^2x\,dx\right)\\ &=1-\left(\int_0^{1}u^2\,du-\int_0^{\pi/4}\tan^4x\,dx\right)\\ &=1-\frac{1}{3}+\int_0^{\pi/4}\tan^4x\,dx\\ &=1-\frac{1}{3}+\frac{1}{5}-\int_0^{\pi/4}\tan^6x\,dx\\ &=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\int_0^{\pi/4}\tan^8x\,dx\\ &\qquad\vdots\\ &=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots-\frac{1}{2^{k+1}-1}+\int_0^{\pi/4}\tan^{2^{k+1}}x\,dx\\ \end{align} }$
したがって
${\displaystyle J_k=I'_k+\int_0^{\pi/4}\tan^{2^{k+1}}x\,dx}$
積分の項を評価すると
${\displaystyle
0<\int_0^{\pi/4}\tan^{2^{k+1}} x\,dx<\int_0^{\pi/4}\left(\frac{4}{\pi}x\right)^{2^{k+1}}\,dx=\int_0^1 u^{2^{k+1}}\cdot\frac{\pi}{4}\,du
=\frac{\pi}{4({2^{k+1}}+1)}
}$
なのではさみうちの原理により
${\displaystyle
\lim_{k\to\infty}\int_0^{\pi/4}\tan^{2^{k+1}} x\,dx=0
}$
したがって
${\displaystyle\lim_{k\to\infty}(I'_k-J_k)=0}$
となることが確認できました!
おわりに
というわけで、私の好きなライプニッツの公式の視覚化の解説でした。
もう一度、最初の図を見てください。
 1-1/3+1/5-1/7+…=π/4の視覚化
1-1/3+1/5-1/7+…=π/4の視覚化
……。いかがでしょうか。うまく言語化できないのであえて語りませんが、私がこの図にこめた思いが少しでも伝わっていればいいなあ、と思います。
しかし、これがベストな視覚化だとは思っていません。
もっと直接的に「$\frac{1}{3}$ は $\frac{1}{3}$ のままで、$\frac{1}{5}$ は $\frac{1}{5}$ のままで直接この式を感じられる」ような視覚化がどこかにありそうな気がしてなりません。
何かアイデア等ありましたら教えていただければ幸いです!
