PILAME杯2025 自分の問題(yo-16,Day2-8)の解説
PILAME杯2025で出題させていただいた問題の解説を放流しようと思います。
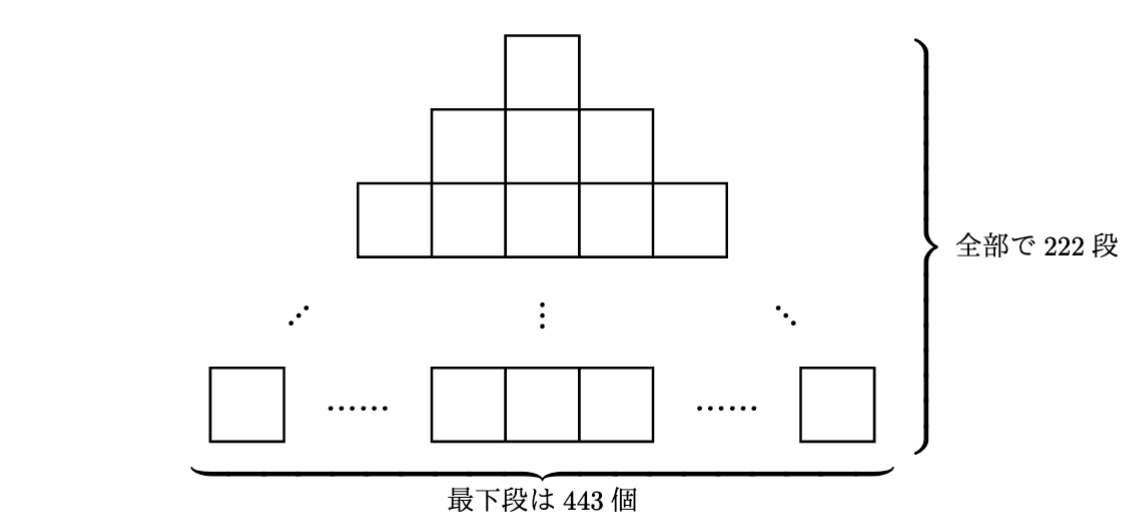
図1の $222^2$ 個のマスからなる図形について,その各マスを白または黒のいずれか $1$ 色で塗ることを考える.このとき,以下の $3$ 条件をすべてみたすような塗り方は何通りあるか.
- 最上段の $1$ マスは黒で塗られている.
- 最下段の $443$ マスには黒で塗られたマスがちょうど $2$ マス存在する.
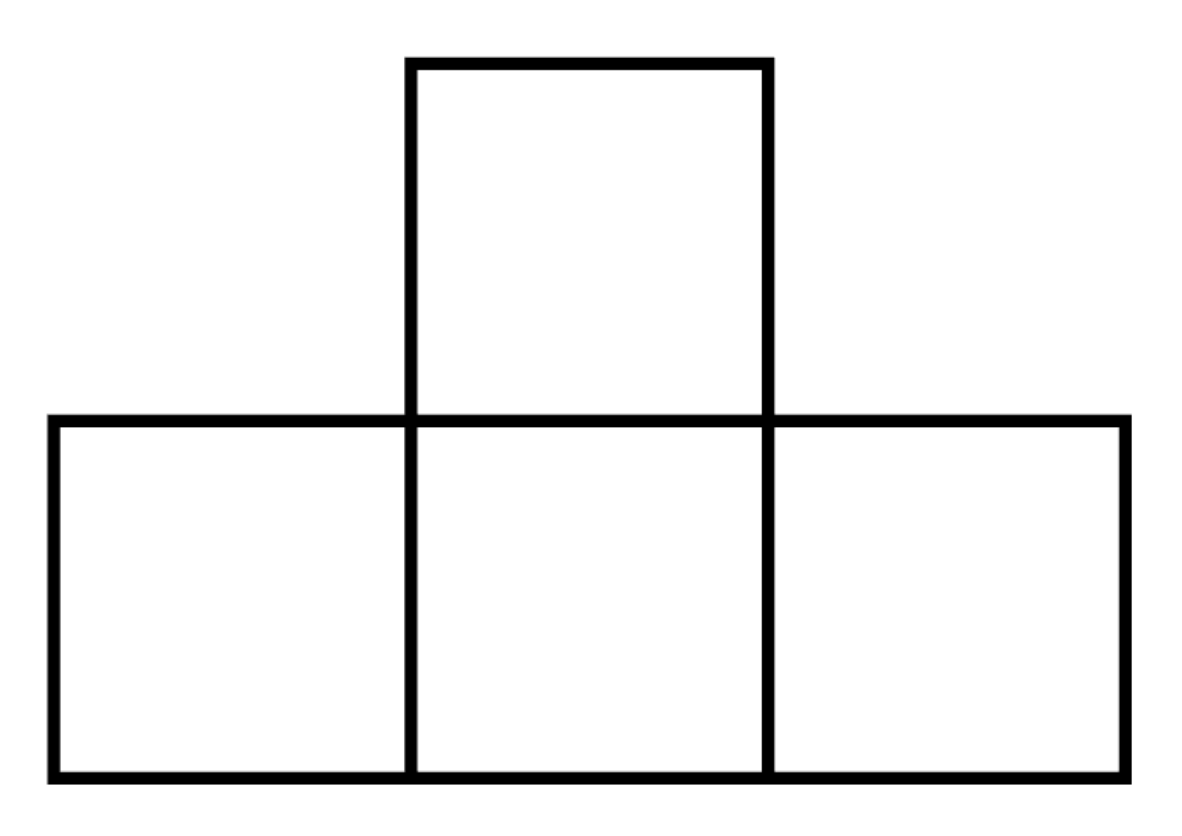
- 図2に示す図形と合同で向きも一致するような任意の $4$ マスの組について,次のいずれかが成立する.
- $4$ マスとも同じ色で塗られている.
- 黒と白で塗られたマスがそれぞれちょうど $2$ マスずつ存在する.
ただし,裏返しによって一致する塗り方は異なるものとして数え,色を塗る順番のみが異なるような塗り方は同じものとして数える.
黒で塗ったマスを $1$ に対応させ,白で塗ったマスを $0$ に対応させることを考える.このとき,$3$ 番目の条件より,最下段を除く任意のマスは,真下のマスと右下のマス, 左下のマスに書き込まれた数の合計を $2$ で割った余りと等しくなる.$i=0,1,\dots,442$ について,最下段の $443$ 個のマスが,左から $i+1$ 個目のマスにのみ $1$ が書き込まれ,それ以外のマスに $0$ が書き込まれている状況を考える.このとき,最下段以外のマスについて,そのマスに書き込まれる数字は,「最下段で $1$ が書き込まれたマスから,真上,左上あるいは右上のいずれかに進むことを繰り返して得られる経路の総数を $2$ で割った余り」であり,特に最上段のマスに書かれる数字は
$$\lbrack x^i \rbrack(1+x+x^2)^{221}$$
を $2$ で割った余りとなる.よって,最下段のマスであって,左から $i+1,j+1$ 個目のマスに $1$ が書き込まれているとき,最上段は
$$\lbrack x^i \rbrack(1+x+x^2)^{221}+\lbrack x^j \rbrack(1+x+x^2)^{221}$$
を $2$ で割った余りと等しくなる.よって,$i=0,1,\dots,442$ のうち $\lbrack x^i \rbrack(1+x+x^2)^{221}$ が奇数となる $i$ の個数を $M$ とすると,求める答えは $M(443-M)$ である.
以下,$2$ つの $x$ の整数係数多項式 $f(x),g(x)$ について,任意の $i$ にて,$\lbrack x^i \rbrack f(x)$ と $\lbrack x^i \rbrack g(x)$ の偶奇が一致するとき,$f(x)\equiv g(x)$ と表す.このとき,整数係数多項式 $f(x)$ について $f(x)^2\equiv f(x^2)$ が成立することから,以下のように計算できる.
\begin{align*}
(1+x+x^2)^3& \equiv (1+x+x^2)(1+x+x^2)^2\\
&\equiv (1+x+x^2)(1+x^2+x^4)\\
&\equiv1+x+x^3+x^5+x^6\\
(1+x+x^2)^7& \equiv (1+x+x^2)(1+x+x^2)^2(1+x+x^2)^{2^2}\\
&\equiv (1+x+x^2)(1+x^2+x^4)(1+x^4+x^8)\\
&\equiv(1+x+x^3+x^5+x^6)(1+x^4+x^8)\\
&\equiv 1+x+x^3+x^4+x^6+x^7+x^8+x^{10}+x^{11}+x^{13}+x^{14}
\end{align*}
よって,
\begin{align*}
(1+x+x^2)^{221}& \equiv (1+x+x^2)^{1+4\times7+64\times3}\\
&\equiv (1+x+x^2)(1+x^4+x^{4\times2})^7(1+x^{64}+x^{64\times2})^3\\
&\equiv(1+x+x^2)\\
&\times(1+x^{4}+x^{4\times3}+x^{4\times4}+x^{4\times6}+x^{4\times7}+x^{4\times8}+x^{4\times10}+x^{4\times11}+x^{4\times13}+x^{4\times14})\\
&\times(1+x^{64}+x^{64\times3}+x^{64\times5}+x^{64\times6})
\end{align*}
上の変形の最後の三行に渡る多項式について,それぞれの行を
\begin{align*}
&\sum_{i=0}^{2}a_ix^i\equiv 1+x+x^2\\
&\sum_{i=0}^{14}b_ix^{4i} \equiv 1+x^{4}+x^{4\times3}+x^{4\times4}+x^{4\times6}+x^{4\times7}+x^{4\times8}+x^{4\times10}+x^{4\times11}+x^{4\times13}+x^{4\times14}\\
&\sum_{i=0}^{6}c_ix^{64i}\equiv 1+x^{64}+x^{64\times3}+x^{64\times5}+x^{64\times6} \\
\end{align*}
とおくと,
$$(1+x+x^2)^{221}\equiv\sum_{i=0}^2\sum_{j=0}^{14}\sum_{k=0}^{6}a_ib_jc_kx^{i+4j+64k}$$
と表されることから,$M=3\times 11\times 5=165$ であり,求める答えは $165(443-165)=\mathbf{45870}$.
はじめ,座標平面上の点 $P$ が点 $(0,0)$ にある.この点 $P$ を $x,\,y$ いずれかの正方向に $1$ だけ移動させる操作を計 $10$ 回繰り返して,点 $(5,5)$ に移動させることを考える.
$0$ 以上 $5$ 以下の整数 $k$ について,点 $P$ が通過した $11$ 個の格子点$^{*}$のうち,その $x$ 座標と $y$ 座標のうち大きくない方が $k$ に等しいものの個数を $n_k$ と定める.
このとき,${}_{10}\mathrm{C}_{5}$ 通りの操作方法すべてについて,積 $n_0 n_1 n_2 \cdots n_5$ を足し合わせた値を求めよ.
*格子点とは,$x$ 座標も $y$ 座標も整数であるような点のことである.
以下の図のように $0$ 以上 $5$ 以下の整数 $k$ について, 点 $P$ が通過した $11$ 個の格子点のうち $\min(x,y)=k$ であるものを $1$ つずつ選び, その点の位置から $z$ 方向に $1$ 進む操作を挿入することを考える.
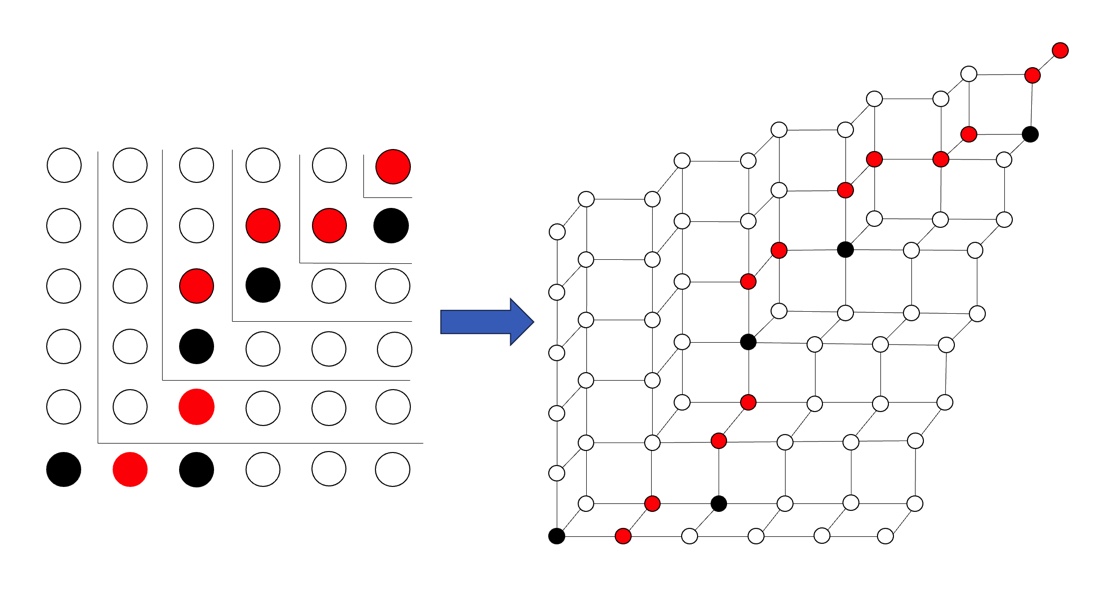
すると, 求めるべき答えは $(0,0,0)$ から $(5,5,6)$ まで以下の条件を満たしながら $x,y,z$ いずれか正方向に $1$ 進むことを繰り返す経路の数である.
- $0$ 以上 $5$ 以下の整数 $k$ について,平面 $z=k$ 上の点 $(x,y,k)$ から $z$ 方向に $1$ 進み $(x,y,k+1)$ に移動するとき, $\min(x,y)=k$ を満たす.
これは, 以下の図のように計算することができる.
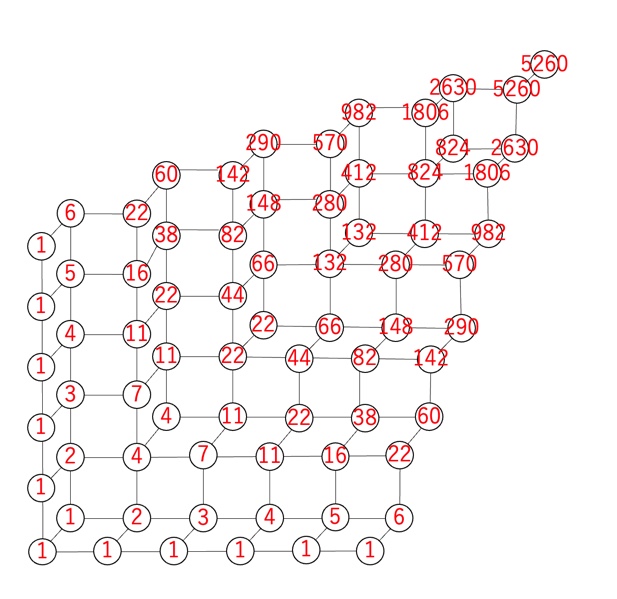
したがって, 答えは $\mathbf{5260}$ となる.
