5/21数学部 暇な人用問題集!!
この記事はある高校の数学部の1年生が解く用の問題を並べています
ですが、ユーザーのみなさんにも是非解いていただきたいのでこの場所を借りて問題を作成しています
そこそこの難易度だと思いますので気軽に解いていってください!!
↑そこそこの難易度(大嘘である)
5/21(水)用問題集 問題
$100!$は$2$で何回割れるか ($100!=1$から$100$までの自然数の総積)
$\sqrt{\frac{1}{1 \cdot 2}+ \frac{1}{2 \cdot 3}+ \frac{1}{3 \cdot 4}+\cdots +\frac{1}{8 \cdot 9}}$を計算せよ
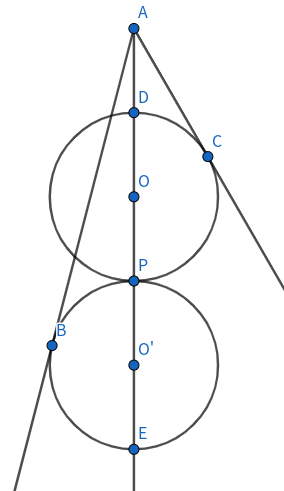
下の図において、$AB=13,AC=5,O'B=OC$である。$\frac{AD}{DO}$を求めよ
 画像の名前
画像の名前
$1 \leq x \leq 2\cdot 10^{2025}$のとき、$x^{x^{2}}=2y^{3}$を満たす自然数の組$(x,y)$の個数を求めよ
難易度:問一 ★☆☆☆☆
問二 ★☆☆☆☆
問三 ★★☆☆☆
問四 ★★★★☆
...
...
...
...
この下に解答があります
...
...
...
...
...
では、解答。
解答
問題1 $97$回
$100!=1\cdot2\cdot3\cdot4\cdot5\cdot6\cdots$が$2$で何回割れるか考える。
$100$までの自然数にある偶数は$50$個であり、それぞれを$2$で割ることができる。このとき、もともと$4$の倍数だった数はまだ素因数に$2$を含む。
$100$までの自然数にある$4$の倍数は25個であり、それぞれをもう一度$2$で割ることができる。このとき、もともと$8$の倍数だった数はまだ素因数に$2$を含む。
同様の議論より、$100!$を$2$で割れる回数は、$100$までの
1.偶数の個数
2.$4$の倍数の個数
3.$8$の倍数の個数
4.$16$の倍数の個数
5.$32$の倍数の個数
6.$64$の倍数の個数
の総和である。よって、$50+25+12+6+3+1=97$回である。
問題2 $\frac{2\sqrt{2}}{3}$
$\sqrt{\frac{1}{1 \cdot 2}+ \frac{1}{2 \cdot 3}+ \frac{1}{3 \cdot 4}+\cdots +\frac{1}{8 \cdot 9}}$
$=\sqrt{(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})+(\frac{1}{3}-\frac{1}{4})+\cdots (\frac{1}{8}-\frac{1}{9})}$
$=\sqrt{\frac{8}{9}}$
$=\frac{2\sqrt{2}}{3}$である。
問題3 $\frac{25}{36}$
$AC,AD,$円$O$について方べきの定理より$AD\cdot AP=25$
$AD,AB,$円$O'$について方べきの定理より$AP\cdot AE=169$
ここで、$\frac{AE}{AD}=\frac{AD+4DO}{AD}=1+4\cdot \frac{DO}{AD}=\frac{169}{25}$であり、整理すると、$\frac{AD}{DO}=\frac{25}{36}$である。
問題4 $\frac{2\cdot 10^{675}+1}{3}$個
以下、合同式を用いるときは全て$3$を法にするものとする。
$n$番目の素数を$p_{n}$と表し、$x=p_{1}^{k_{1}}\cdot p_{2}^{k_{2}}\cdot p_{3}^{k_{3}}\cdots p_{m}^{k_{m}} $であるとする。また、$v_{p}(x)$を、$x$を$p$で割り切れる回数とする。
$x \equiv 0 $のとき、$v_{2}(x^{x^2}) \equiv 0$だが、$v_{2}(2y^3) \equiv 1$であり矛盾。よって$x \equiv \pm 1$を得る。
$x \equiv \pm 1$のとき、$\forall j \in \mathbb{N} $に対し$v_{p_{j}}(x^{x^2}) \equiv k_{j}$であり、$v_{p}(2y^3)$は、
$p=2$で $v_{p}(2y^3) \equiv 1$
$p \geq 3$で $v_{p}(2y^3) \equiv 0$
であるため、$k_{2}\equiv 1 , k_{p \geq3}\equiv0$である。すなわち、$x$は、$3$の倍数でない自然数$t$を用いて$x=2t^3$という形である必要がある。
いっぽう、$t$が$3$の倍数でない自然数のとき、$x=2t^3$は
$(2t^3)^{(2t^3)^2}=2\cdot2^{(2t^3)^{2}-1} \cdot (t^{4t^6})^3=2\cdot2^{(2t^{3}-1)(2t^3+1)} \cdot (t^{4t^6})^3$
$=2\cdot (2^{\frac{(2t^{3}-1)(2t^3+1)}{3} })^3 \cdot (t^{4t^6})^3=2\cdot (2^{\frac{(2t^{3}-1)(2t^3+1)}{3} } \cdot t^{4t^6})^3=2y^3$
より、十分である。
よって、$1 \leq 2t^3 \leq 2\cdot 10^{2025}$を満たす$3$の倍数でない$t$の個数を求める。
$t \leq 10^{675}$であり、$10^{675}-1$までにある$3$の倍数でない自然数は$\frac{2(10^{675}-1)}{3}$個。それに$t=10^{675}$を合算して答えは$\frac{2(10^{675}-1)}{3}+1=\frac{2\cdot 10^{675}+1}{3}$個である。
コメント
最後までお疲れ様でした! 問1,2は常識問題のような部分があるので1分以内に解けるようになりましょう! 問3は、方べきの定理を用いろと言わんばかりの図なので見た目以上にあっさり解けたかと思います。問題は難易度4の問4です。
$x^2$が指数に乗っていたり、$3$が指数に乗っていたりします。もし、これらが指数でなく底にあったならばmod3で一発だというふうになると思います(ならないのであれば、もっと整数問題を解くべきである)。このようなときは、「割り切れる回数」に着目してみましょう。割り切れる回数に含まれる情報は指数の情報です。つまり、「割り切れる回数」を考えることで指数の情報だけに着目し、mod3を使える形にしたわけです。この発想さえあればあとは余裕で解けることでしょう。
今回の問題はいかがでしたでしょうか。少しでも面白かった/ためになったと思った方はぜひフォローのほどよろしくお願いします!
ではまたどこかで...
