領域求積問題(自作・数III)
まえがき
こんにちは、高3のぱぺです。
もうすぐ8月ですね。勉強しなきゃいかんのに、夏期講習等きっかけがないと自習室にも行かずダラダラしてしまうので、注意しないといけないですね。
本題
今回は積分を使った問題を出します。
問題
$A\;(1,-1,0),\;B\;(1,1,0),\;C\;(-1,1,0),\;D\;(-1,-1,0)$の$4$点を頂点とする正方形$ABCD$がある。また、平面$ABCD$上で正方形$ABCD$に内接する円を$K$とする。
正方形$ABCD$の周$ABCDA$上に点$P$をとり、それを中心として円$K$に外接する$(*1)$ような球$\Gamma$を考える。ただし、点は半径$0$の球であると考えることができるとする。
$(*1)$「円$K$に外接する」とは、円$K$(周及び内部)と球(球面及び内部)がただ$1$点を共有することを指す。
以降、「球$\Gamma$」はその球面及び内部の領域を表す。
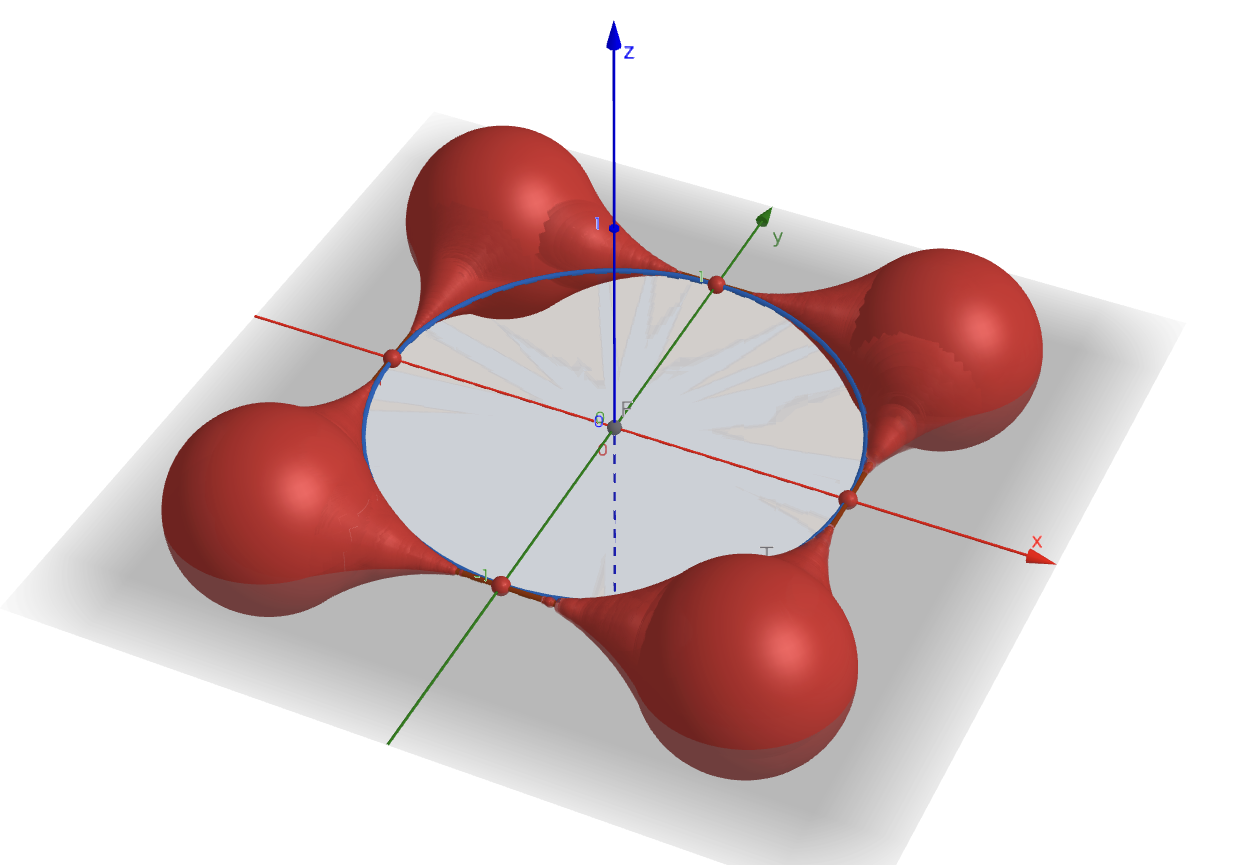
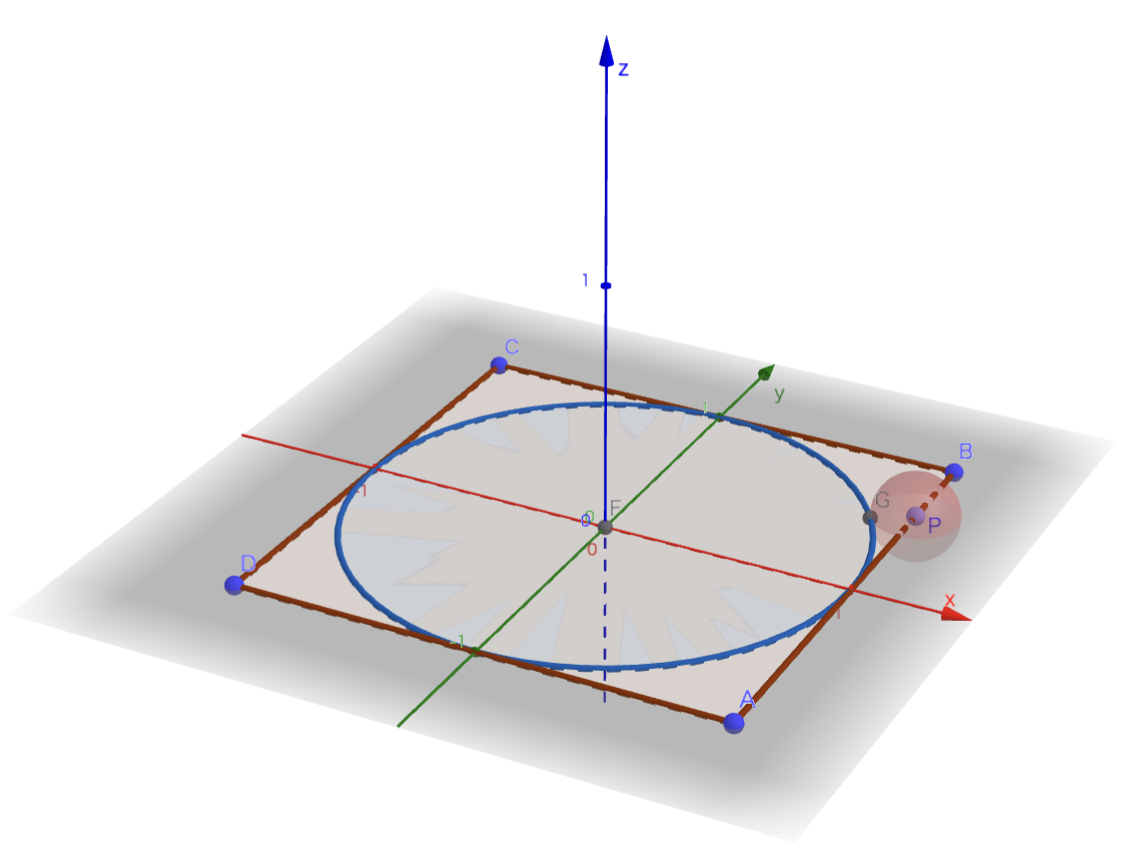 GeoGebraで描画したもの
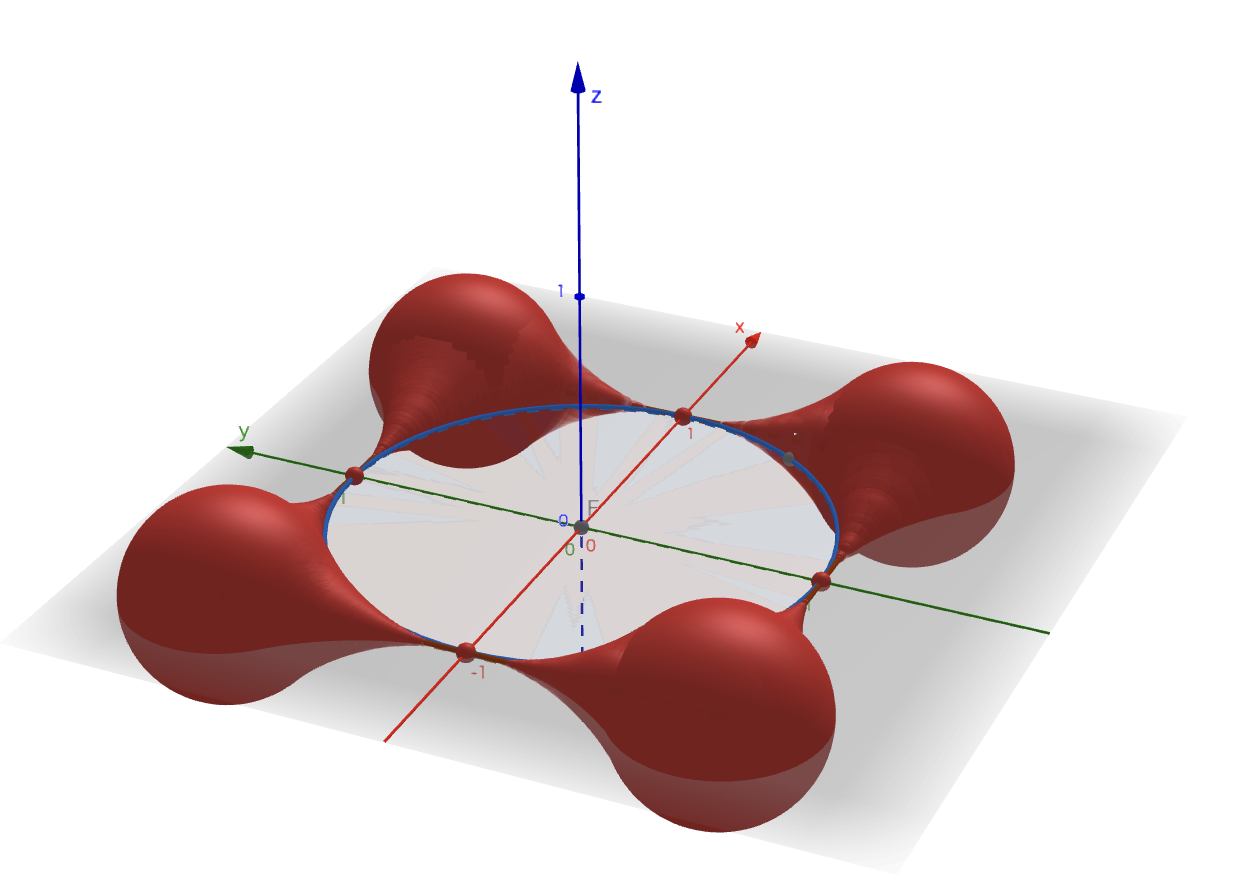
GeoGebraで描画したもの
$\text{(1)}$ 点$P$が両端点を含む線分$AB$上をくまなく動くとき、球$\Gamma$の通過する領域は、直線$AB$をまたがないある平面図形$F$を軸$AB$周りに回転させた回転体であると考えることができる。
そのような図形$F$の概形を、以下の【条件】に則って、与えられた図に示せ。
【条件】
・回転軸$AB$を$X$軸におき、$A,B$の位置を揃え、図形$F$は領域$Y\geq0$に含まれるように図示する。
・図形の境界について言及する。
【図】
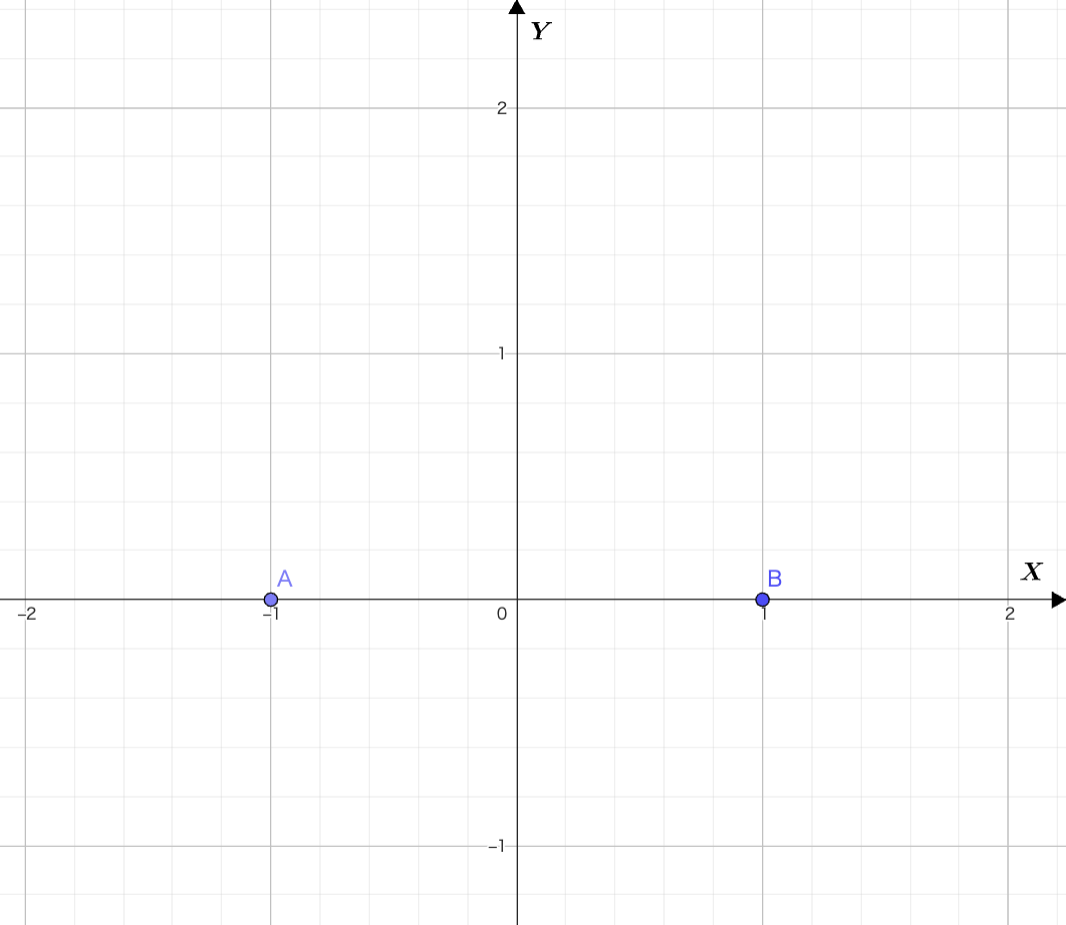 与えられた図
与えられた図
$ $
$ $
$\text{(2)}$ 点$P$が正方形$ABCD$の周$ABCDA$上をくまなく動くとき、球$\Gamma$の通過する領域の体積を求めよ。
$ $
$ $
解説
$\text{(1)}$
線分$AB$上を球$\Gamma$がくまなく動くとき、その通過領域は回転体であり、図形$F$の形状に関しては、断面のひとつとして$z=0 \;, \; x\leq1$の部分をもとに考えればよい。
![!FORMULA[45][1159839][0]平面。!FORMULA[46][37360][0]軸はベクトル!FORMULA[47][1305882576][0],!FORMULA[48][37391][0]軸はベクトル!FORMULA[49][897177675][0]の方向, 原点は点!FORMULA[50][-2102504560][0]にある。](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FRgxk9GnCHKx3iUzD2NpT.png?alt=media) $XY$平面。$X$軸はベクトル$(0,1,0)$,$Y$軸はベクトル$(-1,0,0)$の方向, 原点は点$(1,0,0)$にある。
$XY$平面。$X$軸はベクトル$(0,1,0)$,$Y$軸はベクトル$(-1,0,0)$の方向, 原点は点$(1,0,0)$にある。
図3のように座標軸をとる。球$\Gamma$を$z=0$で切断した断面のうち$Y\geq0$にあたる半円を$\Gamma '$とする。
$ $
ここで、図形$F$は$Y$軸対称であるから、その$X\geq0$の部分($G$とする)について考える。
図4を参照する。
半円$\Gamma '$と円$K$との接点を$T$とする。$T$で円$K$に接し、半直線$TP$上に中心をとってつくる半径$\sqrt{2}-1$の円を「大円」と呼ぶことにする。
半円$\Gamma '$は明らかに大円に含まれるため、点$P$が線分$AB$の$X\geq0$の部分をくまなく動くときの大円の通過領域(青色着色・境界線含む)は、領域$G$を完全に含む。
なお領域$G$は、「半径$1$の円$K$の外側を半径$\sqrt{2}-1$の大円が滑らずに中心角$\displaystyle \frac{π}{4}$だけ動いたときの大円の通過領域」と考えることができるため、青色の領域となる。
また、半円$\Gamma '$は常に領域$Y\geq0$に含まれるから、領域$G$は常に$Y\geq0$に含まれる。
従って、領域$G$は、「青色着色の領域で$Y\geq0$の部分」($G_{\text{over}}$とする)に完全に含まれる。このとき、$G_{\text{over}}:0\leq Y\leq f(X)$
ただし、$f(X)=\begin{cases}\displaystyle
1-\sqrt{1-X^2} &\quad \left(0\leq X \leq \frac{1}{\sqrt{2}}\right) \\
\sqrt{(\sqrt{2}-1)^2-(X-1)^2} &\left(\frac{1}{\sqrt{2}}< X\leq \sqrt{2} \right)
\end{cases}$
![大円の通過領域。境界は!FORMULA[86][36244][0]つの円弧でできており、各々
①中心!FORMULA[87][37081][0]・半径!FORMULA[88][-707440430][0]・中心角!FORMULA[89][-1677763278][0]の弧
②中心!FORMULA[90][37081][0]・半径!FORMULA[91][-872856024][0]・中心角!FORMULA[92][-1677763278][0]の弧
③中心!FORMULA[93][1526237825][0]・半径!FORMULA[94][-707440430][0]の半円
④中心!FORMULA[95][-1217829044][0]・半径!FORMULA[96][-707440430][0]の半円
である。](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FhpLgpQBxwNb9neH6i1tV.png?alt=media) 大円の通過領域。境界は$4$つの円弧でできており、各々
大円の通過領域。境界は$4$つの円弧でできており、各々
①中心$O$・半径$\sqrt{2}-1$・中心角$\frac{π}{4}$の弧
②中心$O$・半径$2\sqrt{2}-1$・中心角$\frac{π}{4}$の弧
③中心$(0,1-\sqrt{2})$・半径$\sqrt{2}-1$の半円
④中心$(1,0)$・半径$\sqrt{2}-1$の半円
である。
$ $
$ $
$0\leq X_0\leq1$に対して、$X=X_0$を満たす点$(X,Y)$のうち領域$G$に含まれるようなものの$Y$の範囲を考える。
$ $
$0\leq X_0 \leq 1$のとき、図から明らかに、$0\leq Y \leq 1-\sqrt{1-X_0^2}$(円$K$の下側)である。
このとき、$Y=1-\sqrt{1-X_0^2}$となるのは、半円$\Gamma '$が$X=X_0$で接するときのみである。
球$\Gamma$の中心$P$は$0\leq X \leq 1, \; Y=0$を動くから、半円$\Gamma '$と円$K$の接点の$X$座標のとりうる値の範囲は$\displaystyle 0\leq X\leq \frac{1}{\sqrt{2}}$.
$\displaystyle 0\leq X_0\leq\frac{1}{\sqrt{2}}$のとき、半円$\Gamma '$が$X=X_0$で接するときが存在するため、$Y$のとりうる値は$0\leq Y\leq 1-\sqrt{1-X_0^2}$である。
$ $
$\displaystyle X_0>\frac{1}{\sqrt{2}}$のとき
領域$G$の$\displaystyle \frac{1}{\sqrt{2}}< X$ の部分は、領域$G_{\text{over}}$の$\displaystyle \frac{1}{\sqrt{2}}< X$の部分$\left(0\leq Y\leq \sqrt{(\sqrt{2}-1)^2-(X-1)^2} \left(\frac{1}{\sqrt{2}}< X\leq \sqrt{2} \right)\right)$に含まれる。
また、領域$G$は$P=(1,0)$のときの半円$0\leq Y\leq \sqrt{(\sqrt{2}-1)^2-(X-1)^2}$を含む。
したがって、領域$G$の$\displaystyle \frac{1}{\sqrt{2}}< X$ の部分はちょうど$\left(0\leq Y\leq \sqrt{(\sqrt{2}-1)^2-(X-1)^2} \left(\frac{1}{\sqrt{2}}< X\leq \sqrt{2} \right)\right)$
以上から、領域$G$はちょうど領域$G_{\text{over}}$に一致する。
![領域!FORMULA[138][1832394031][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FPGfOZcumSmLkjQQOSlXE.png?alt=media) 領域$G\quad (=G_{\text{over}})$
領域$G\quad (=G_{\text{over}})$
領域$G$を$Y$軸に関して反転させたものと併せると領域(図形)$F$となる。
![領域!FORMULA[142][36802][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FUJHJOYI3spPgdUTBpOGA.png?alt=media) 領域$F$
領域$F$
従って、求める平面図形$F$の概形は上図。ただし境界を含む。
$ $
$ $
$ $
$ $
$ $
$ $
$\text{(2)}$
他の辺に関しても$\text{(1)}$と同様に動く。
点$P$が辺$e$上をくまなく動く際の球$\Gamma$の通過領域を$D_e$とする。
このとき、
$D_{AB}$と$D_{BC}$は中心$B$,半径$\sqrt{2}-1$の球を共有する。
$D_{BC}$と$D_{CD}$は中心$C$,半径$\sqrt{2}-1$の球を共有する。
$D_{CD}$と$D_{DA}$は中心$D$,半径$\sqrt{2}-1$の球を共有する。
$D_{DA}$と$D_{AB}$は中心$A$,半径$\sqrt{2}-1$の球を共有する。
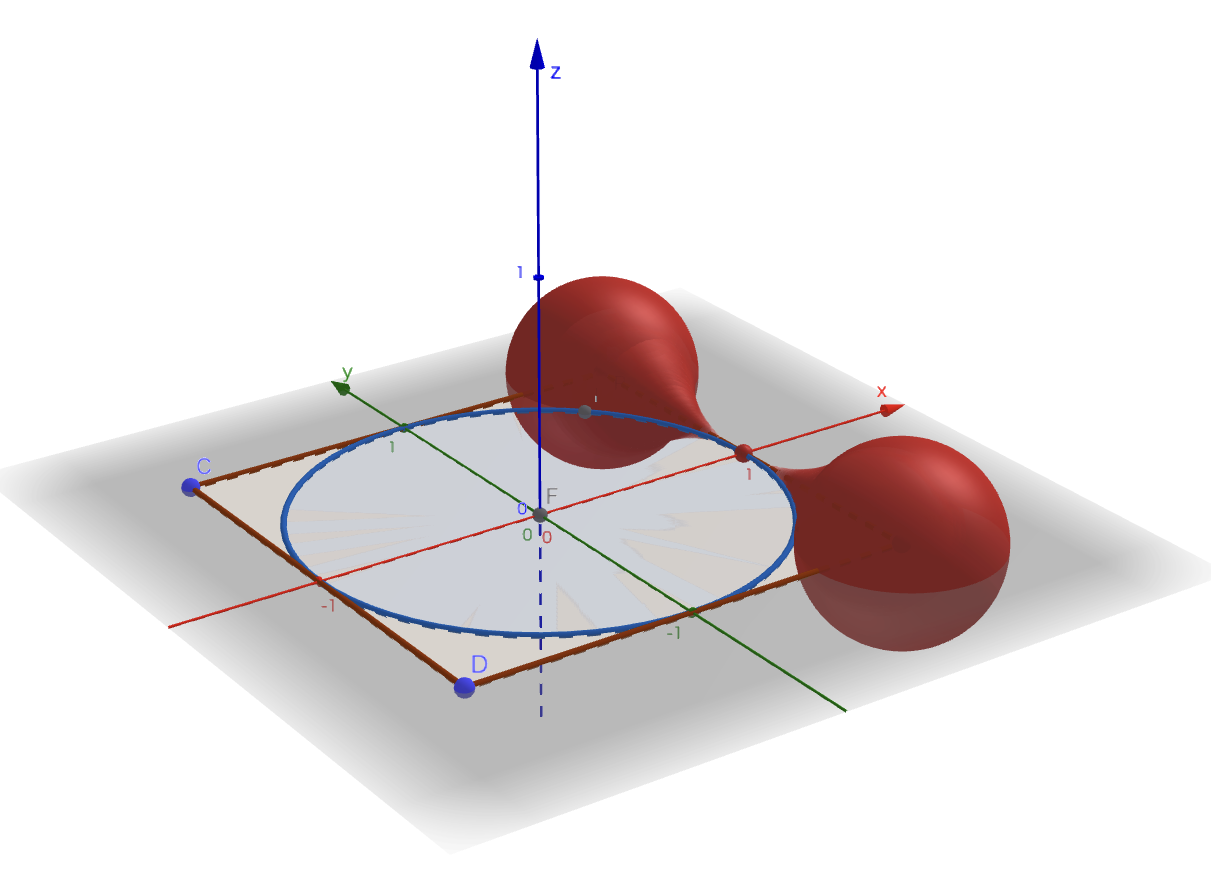
【$D_{AB}$の概形】
表示の関係上、軸上で点$P$がそのまま描画され、小さい球のようなものが存在するように見えてしまっているが、ここは半径$0$である。
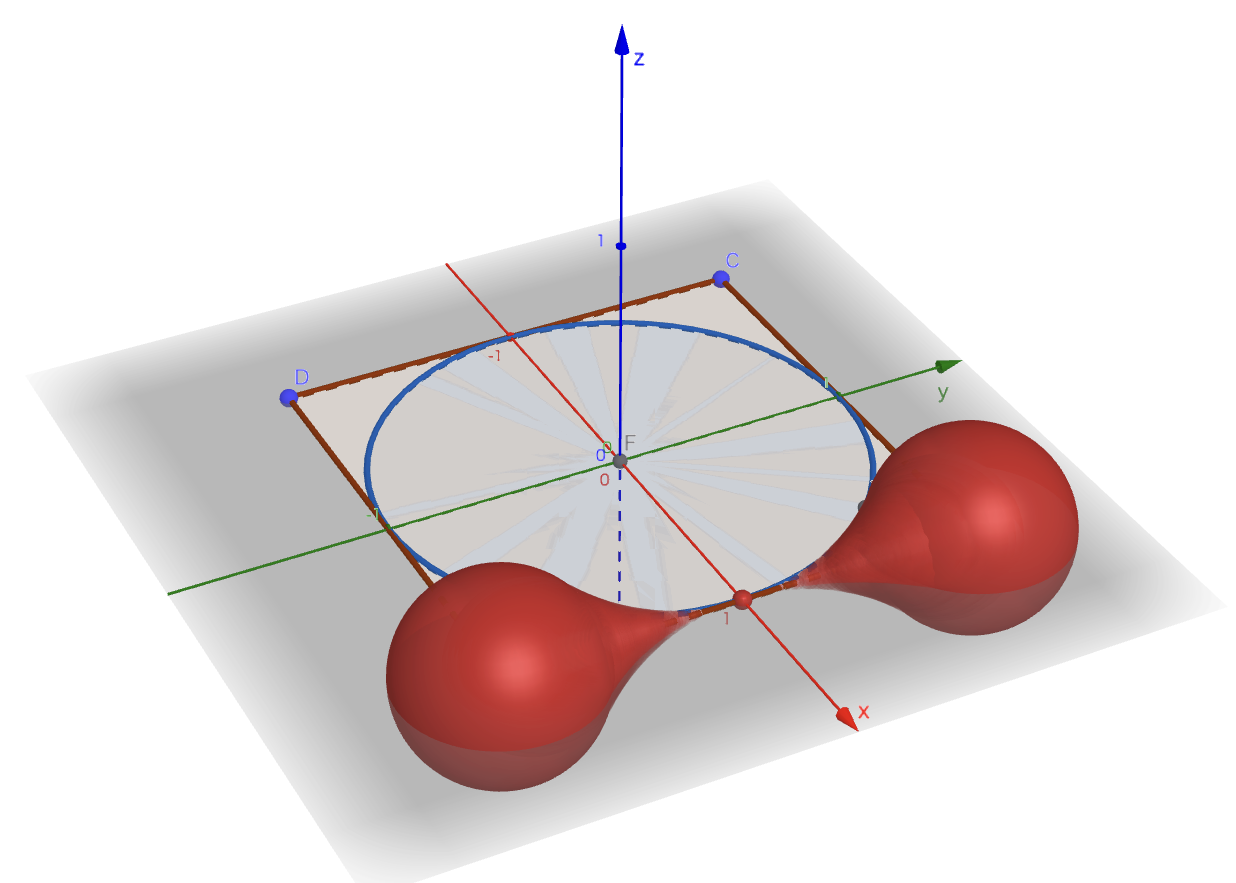
【求める領域の概形】
表示の関係上、軸上で点$P$がそのまま描画され、小さい球のようなものが存在するように見えてしまっているが、ここは半径$0$である。
従って、
$D_{AB}$の$\displaystyle \abs{X}\leq\frac{1}{\sqrt{2}}$ の部分の体積を$V_1$,
半径$\sqrt{2}-1$の球の体積を$V_2$,
半径$\sqrt{2}-1$の球$x^2+y^2+z^2=(\sqrt{2}-1)^3$の$\displaystyle \frac{\sqrt{2}-1}{\sqrt{2}}\leq x\leq\sqrt{2}-1$の部分の体積を$V_3$とすると、
領域$D_{AB},D_{BC},D_{CD},D_{DA}$の体積はいずれも$V_1+2V_2-2V_3$で表される。
求める体積を$V$とすると、$V=4(V_1+2V_2-2V_3)-4V_2=4(V_1+V_2-2V_3)$である。
$r=\sqrt{2}-1$として、
\begin{aligned}
V_1 &=2\pi\int_{0}^{\frac{1}{\sqrt{2}}} \left\{1-\sqrt{1-x^2}\right\}^2 dx \\
&=-\frac{π^2}{2}+\left(\frac{11}{6}\sqrt{2}-1\right)π \\
V_2 &=\frac{4}{3}πr^3 \\
V_3 &= \pi r^3\int_{\frac{1}{\sqrt{2}}}^{1} \left\{\sqrt{1-x^2}\right\}^2 dx \\
&= \left(\frac{2}{3}-\frac{5}{12}\sqrt{2}\right)πr^3
\end{aligned}
であるから、
\begin{aligned}
&V_1+V_2-2V_3 \\
&=\left\{ -\frac{π^2}{2}+\left(\frac{11}{6}\sqrt{2}-1\right)π \right\}+\left\{\frac{4}{3}-2\left(\frac{2}{3}-\frac{5}{12}\sqrt{2}\right)\right\}πr^3 \\
&=\left\{ -\frac{π^2}{2}+\left(\frac{11}{6}\sqrt{2}-1\right)π \right\}+\frac{5}{6}\sqrt{2}πr^3 \\
&=-\frac{π^2}{2}+\left\{\left(\frac{11}{6}\sqrt{2}-1\right)+\frac{5}{6}\sqrt{2}(\sqrt{2}-1)^3\right\}π \\
&=-\frac{π^2}{2}+\left(\frac{22}{3}-4\sqrt{2}\right)π
\end{aligned}
これを用いて
\begin{aligned}
V&=4(V_1+2V_2-2V_3) \\
&=-2π^2+\frac{8}{3}\left(11-6\sqrt{2}\right)π
\end{aligned}
以上から、$\displaystyle V=-2π^2+\frac{8}{3}\left(11-6\sqrt{2}\right)π \qquad (\approx 1.3280\cdots)$.
あとがき
$\text{(1)}$の図形$F$で、$\displaystyle \abs{X}\geq\frac{1}{\sqrt{2}}$の概形を求めるところですが、ちょうど数日前(7/29)に思いついたもので、我ながらいい発想だなあと思いました。わざわざ微分をする必要がなくなるんですよね。領域についての必要十分条件ってこういうことなのかなと思いました。
それから、これを平面に置き換えたバージョンも作れます。球$\Gamma$を円$\Gamma$にする話ですね。先ほどと同様、ひらめけば微分を使わずに攻略できるようになっているので、気になる方はぜひ挑戦してみてください。今度数研の問題に出そうかと考えています。
更新欄
2025/7/30.19:00 ほぼ完成
2025/7/31.10:25 投稿
