数当てカードを作る
はじめに
本稿は執筆途中である。基本編はあらかた書いたが、応用編はボチボチ続きを書いていく。
呼び方はいろいろあると思うが、特別なカードを用いて相手が思った数を当てる、数当てマジックとかいうものがある。典型的なものとしては、次のような$5$枚のカードを用いる手品で、演者が客に思い描いた日付 ($1$から$31$の自然数) を当てるものがある。日付は誕生日でもいいし、好きな日でもいい。
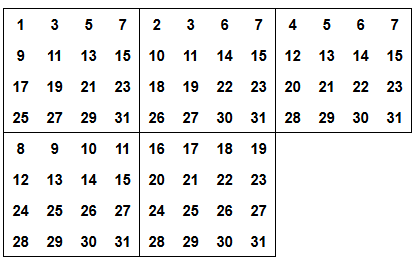数当てカードの例 (日付当てカード)
演者は客に「思った日付が含まれているカード以外は裏返してください」と言い、客によるその操作が終わった後、表になっているカードの左上の数の和を「あなたが思った数は◯ですね」と言う、という流れである。
こういう数当てカードをいろいろ作ってみたいと思ったので、考えてみたのが本稿である。
当てるのは数じゃなくてもいいし、使うのがカードじゃなくてもいいのだが、とりあえず、数当てカード、という呼称にしておく。
数当てカードの数理
シンボルとマークおよびそれらの間に成り立つ配置
先に当てる対象のものを「数じゃなくてもいい」と書いたが、これをシンボルと呼ぶことにする。
シンボルの集合 $\check{S}$,マークの集合 $M$ を考える。シンボルからマークへの写像 $\check{f}$ 全体の集合は、すなわち、配置集合 $M^\check{S}$ である。
$$
M^\check{S} = \defset{\check{f}}{\check{f}:\check{S} \rightarrow M }
$$
写像 $\check{f}$ の定義域 $\check{S}$ を、その部分集合 $S$ に制限した写像を $f$ とする。つまり、
$$
f : S \rightarrow M, \;\; f \in M^S \;\;, \forall x \in S; f(x) = \check{f}(x) .
$$
本稿では、「配置」と称した場合、$M^S$ もしくは $M^\check{S} $ の元を指すものとする。
「日付当てカード」の場合、シンボルの集合 $S$ は $1$から$31$までの自然数である。
マークの集合 $M$ は、たとえば 2進数表示の各桁の数 $\left\{ 0, 1 \right\}$ と考えることができる。
そして、カードそれぞれが配置、すなわち $S$から $M$ への写像を表わしている。$k$枚目のカードは、$S$の元$x$を2進数表記したときの$k$桁目を $f_k(x)$ として、それが $1$ になるものだけが書かれている。
列
ここで、ある集合 $\Lambda$ の元 $\lambda$ の列、$\boldsymbol{\lambda} = \mseq{\lambda_1, \lambda_2, \cdots, \lambda_m} $ を考える。
まず、空列 $\mseq{} $ を考える。これは長さ 0 の列であり、形式的に $\Lambda^0$ の元とする ($\Lambda^0$ はただ一つの元 $\mseq{}$ を持つ集合とする)。
$$
\mseq{} \in \Lambda^0 = \left\{ \mseq{} \right\} \\
$$
長さ $m \;(m>0)$ の列 $\overset{m}{\blambda} $ は 、$\Lambda$ の $m$ 個分の直積 $\Lambda^m = \Lambda \times \Lambda \times \cdots \times \Lambda $ の元である ($\overset{m}{\blambda} \in \Lambda^m $)。
$\overset{m}{\blambda} $ は長さ $m-1$ の列 $\overset{m-1}{\blambda}$ に $m$ 番目の要素 $\lambda_m$ を追加したもの、と定義する。
$$
\overset{m}{\blambda} = \mseq{\overset{m-1}{\blambda}, \lambda_m}
$$
再帰的に展開していくと、
$$
\overset{m}{\blambda} = \mseq{\overset{m-1}{\blambda}, \lambda_m} = \mseq{\mseq{\overset{m-2}{\blambda}, \lambda_{m-1}}, \lambda_m} = \cdots = \mseq{\mseq{\mseq{\mseq{\mseq{}, \lambda_1}, \lambda_2}, \cdots }, \lambda_m}
$$
となるが、これを次のように略記できるものとする。
$$
\overset{m}{\blambda} = \mseq{\mseq{\mseq{\mseq{\mseq{}, \lambda_1}, \lambda_2}, \cdots }, \lambda_m} = \mseq{\lambda_1, \lambda_2, \cdots , \lambda_m}
$$
また、誤解のおそれがない場合には、$\overset{m}{\blambda}$ の列長を表す $m$ を省略して $\blambda$ と記す。
配置列と配置セット
シンボル $x \in S$ に対して配置 $f$ が与えられると、一つのマーク $a
= f(x) \in M$ が決まる。複数の配置 $f_1, f_2, \cdots, f_m$ に対しては、それぞれにマーク $a_1\!=\!f_1(x),\; a_2\!=\!f_2(x),\; \cdots,\; a_m\!=\!f_m(x)$ が定まる。
この関係を、列を用いてまとめて記述すると次のようになる。
$$
x \in S,\; \overset{m}{\boldsymbol{f}} \in (M^S)^m, \; \overset{m}{\boldsymbol{a}} \in M^m, \;
\overset{m}{\boldsymbol{f}} (x) = \overset{m}{\boldsymbol{a}}
$$
なお、列 $\boldsymbol{f} = \mseq{f_1, f_2, \cdots, f_m} $ 内での要素の順番を問わず、要素全体としてだけ意味を持つ場合もあるので、その場合は $\mathcal{F} = \defset{f_k}{ \boldsymbol{f} = \mseq{f_1, f_2, \cdots, f_m} }$ で表現し、配置セットと呼ぶことにする。
「日付当てカード」の場合、5枚のカードひと揃いが配置セットである。
この要素を特定の順番に並べたものが配置列である。
「使える」配置セットと逆配
$\boldsymbol{f} : S \rightarrow (M^S)^m $ が単射なら、$\boldsymbol{f}$ を「使える」配置列と呼ぶ。
また、これに対応する配置セット $\mathcal{F}$ を「使える」配置セットと呼ぶ。
「使える」配置列 $\boldsymbol{f}$ は単射なので、左逆写像 $\boldsymbol{g} : \text{Im}\boldsymbol{f} \rightarrow S $ が存在する。ここで $\text{Im}\boldsymbol{f}$ は $\boldsymbol{f} $ による $S$ の像であり、当然$M^m $の部分集合である。
$$
\forall x \in S; \; \boldsymbol{g}(\boldsymbol{f}(x)) = x \;,
$$
また、
$$
\forall a,b \in \text{Im}\boldsymbol{f}; \; a \neq b \Longrightarrow \boldsymbol{g}(a) \neq \boldsymbol{g}(b) \;.
$$
この逆写像$\boldsymbol{g}$を本稿では「逆配」と呼ぶことにする。
なぜ、$\boldsymbol{f}$ が単射の場合に「使える」のかと言えば、単射なら逆配が構成できるので、あるシンボル $x$ から算出されるマーク列 $\boldsymbol{a}$ から、元のシンボル $x$ を一意に求めることができるからである。
「日付当てカード」の場合、$\boldsymbol{f}$ が単射なので、5枚のカードひと揃いは「使える」配置セットである。
逆配$\boldsymbol{g}$ は次のように書ける。
$$
\boldsymbol{g}(\langle a_1,a_2,a_3,a_4,a_5\rangle) = \sum_{k=1}^5 a_k\cdot2^{a_k-1}
$$
数当てカードを使った演技
望しい特徴
次に、実際に演技することを考慮して、望しい配置セットの持つべき特徴について考えていく。
数当てカードを使った演技を整理すると次のようになる。
- 演者は客にシンボルの集合 $S$ を示し、客に任意の元 $x \in S$ を選んでもらう。$x$の具体的な値が何かは、演者に秘密にしたままにしてもらう。
- 演者はあらかじめ用意してある配置セット$\mathcal{F}$ からひとつずつ配置 $f \in \mathcal{F} $ を示し、客に $f(x)$ がどのマークになるかを教えてもらう。
- 演者は客が示したマーク列 $\boldsymbol{a}$ を元に $\boldsymbol{g}(\boldsymbol{a})$ を計算し、客が選んだ $x$ を算出し、客に示す。
これが手品 (マジック) として成立するためには、すなわち、客にちょっと不思議な感覚を抱いてもらうためには、いくつかの条件がある。
- シンボルの集合 $S$ の濃度 $|S|$ が小さすぎると当てずっぽうでも当る確率が増えるので不思議さが減ってしまう。客が $x \in S$ を選ぶのが困難にならない限り、$|S|$ は大きい方がよい。【選択容易性】
- $\boldsymbol{f}(x)$ の計算は、客が簡単にできるものでなければならない。【順計算容易性】
- 演者による逆配を用いた計算 $\boldsymbol{g}(\boldsymbol{a})$ は、自然な流れのなかですばやくできるものでなければならない。ただし、【逆計算容易性】【逆計算察知困難性】
マーク
シンボルとして自然数を使う場合
シンボルとして自然数を使うと便利な点が多い。
まず、$|S|$がある程度大きくても、【選択容易性】が高く、【逆計算容易性】も高く設計することが可能である。
作品例
草wカード
草冠の漢字一文字植物の名前になっているものを 16 文字書いた「一覧カード」からひとつ客に選んでもらう。演者は穴開きカードを一枚ずつ一覧カードの隣に置き、選んだ字がその穴開きカードに書かれているか聞く。演者は穴開きカードを裏返して重ねていくが、その際、客が「ある」と言ったカードは「芋」の字が下側になるように重ね、「ない」と言ったカードは「芋」の字が上になるように重ねる。裏向きの穴開きカード4枚をそのまま一覧カードに載せると、客が選んだ字のところにだけ穴が空いていて読めるようになっている。当然「芋」は一覧カードに載っていないので選ばれることはない。
穴開きカードを裏返しながら重ねるとき、持ったカードを左右に返すか、上下に返すかで「芋」の位置をコントロールできるので、自然な動作でやることを心掛ける。また、重ねているときは乱雑に置いていき、最後に手の中で揃えて穴の位置を確認すると不思議さが増すかもしれない。
最後に自分が選んだ漢字ひとつだけが穴から覗いているのを見せる演出でもいいかもしれない。
草wカード
