Ricci flowとリーマン面の一意化定理

これは駒場理数サークルの 豚汁アドベントカレンダー2025 の12日目の記事です．

2025/11/12:向き付け不可能曲面に関するリマークを追記しました。

はじめに

初めまして．南無三坊主ヶ原高校 a.k.a. TOKYO伝説と申します．
秋，豚汁の秋　ということで，まあ寒空の下で食う熱々の豚汁はとても美味しいですよね．そんな時，誰しも一度は冷えてゆく汁物を見て一度はこう思ったことがあるのではないでしょうか．
「温度じゃなくて，リーマン多様体の計量が熱流で時間発展したらどうなるんだろう．」
これは非常に自然で良い疑問でして，一般にリーマン多様体上の関数$f$を熱方程式
$$\frac{\partial f}{\partial t} = \Delta_g f$$
で時間発展させるということは自然に考えられるものですが，Levi-Civita接続のcompatibilityから上の方程式に計量$g$をそのまま代入しても右辺が消えてしまいますし，さらにそもそも微分作用素$\Delta_g$は計量$g$に依存しているので「"熱方程式のようなもの"で多様体上の計量を発展する」ということをナイーブに定式化しようとすると困難が伴います．
そんな中，リッチフローは，熱方程式に類似する嬉しい性質を持った幾何学的フローであり，ペレルマンによるポアンカレ予想の解決への応用など，華々しい応用を数多く持っている理論です．本記事はそのリッチフローの簡単な紹介と，応用の一つとしてコンパクトリーマン面の一意化定理(Uniformization theorem)を紹介します．

この記事を読むにあたって

この記事はあくまでリッチフローを概観する目的で書かれたもので，定義のwell-definednessや細かい正当性については議論しない．気になった人は例えばCK,Topを参照してみてほしい．
$(M,g)$は簡単のため全て閉多様体(コンパクト，境界なし)とし，接続$\nabla$はLevi-Civita接続を考える．(接続を知らない読者は，微分，グラディエントのようなものだと思ってもらえれば良い．)

前提知識について，曲面論やリーマン幾何学，そしてPDEについての知識があると読みやすいと思われるが，ボールやドーナツのようなものをぐにゃぐにゃと変形しているんだなという程度の直感的でふわっとした理解でも読めるように心がけた．

リーマン多様体と曲率

リッチフローとは，リッチ曲率という曲率(空間の曲がり方)に深く関係する概念である．リッチフローを扱う前に，まずはリーマン多様体とその曲率について例を見ることでイメージを膨らませよう．
リッチ曲率は関数ではなく(正確にはテンソルと呼ばれる量)，イメージが難しいが，二次元の場合には，曲面論などでも登場するガウス曲率$K$という関数と直接的な関係がある．
ここで典型的なリーマン多様体とその曲率をみてみよう．

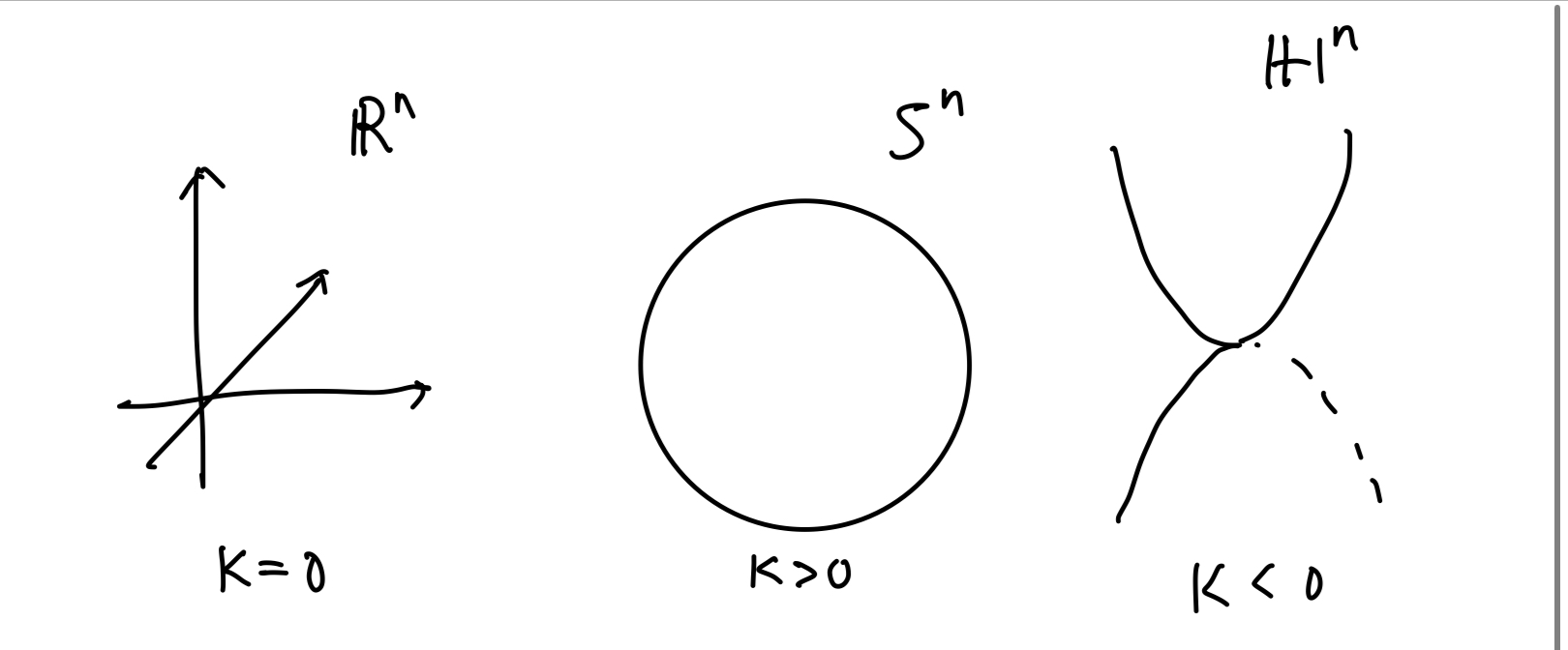ユークリッド空間，球，双曲空間
双曲空間は馬の鞍のような形である．手書きが絶望的ではあるが気になったら双曲平面(hyperbolic surface)等で検索してほしい．

フォーマルな定義は次のように与えられる．ここら辺の細かい定義は知らなくてもフィーリングで読めるようには書いたつもりであるが，形式上導入しておく．これらについて詳しくはLee,Cha,Sakなどを参照．

二次元の場合には，次の関係が成り立ち，
$$\Ric=\frac R2 g$$
$R$はガウス曲率$K$と$$ R=2K\tag{1}$$ の関係にある．

リッチフローとは

厳密な定義は，次のように与えられる．

(特に計量を時間発展する人間は自分が今どの計量を扱っているか明記するために$\Ric(g)$や$\Delta_g$のようにgを明記することが多い)

ある計量$g_0$を「リッチフローで発展する/流す」という場合には次のような初期値問題を考えていると思っていい：
\begin{cases} \dt{g}=-2\Ric(g) \\ g(0)=g_0 \end{cases}
とりあえず二次元の曲面をリッチフローで流してみよう．二次元の時は，リッチ曲率はガウス曲率$K$を用いて$\Ric(g)=Kg$と書かれ，リッチフローの方程式(RF)は$$\dt{g}=-2Kg\tag{2RF} \label{2RF}$$と書ける．
まず，下のような図形を観察しよう．
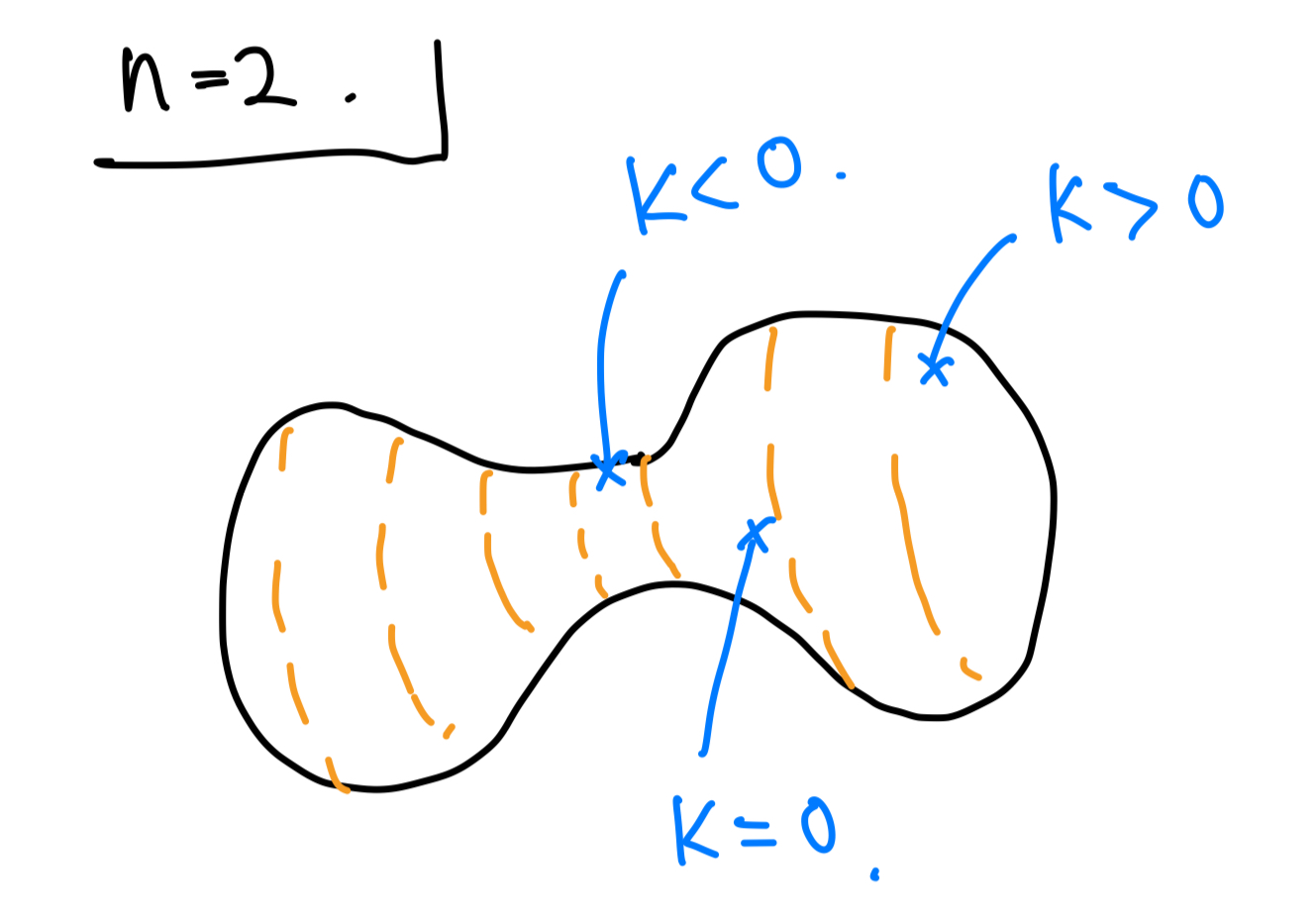ダンベルの形の曲面
図の$K> 0$の箇所において，方程式(2RF)はすなわちgの"収縮"を意味し，$K < 0 $の箇所では逆に"拡大"を意味する．
(曲面論を知っている人は計量の定数倍の変化$g\mapsto λg$におけるガウス曲率や体積要素の変化を計算してみると良い．)
従って，次のような時間発展をする．
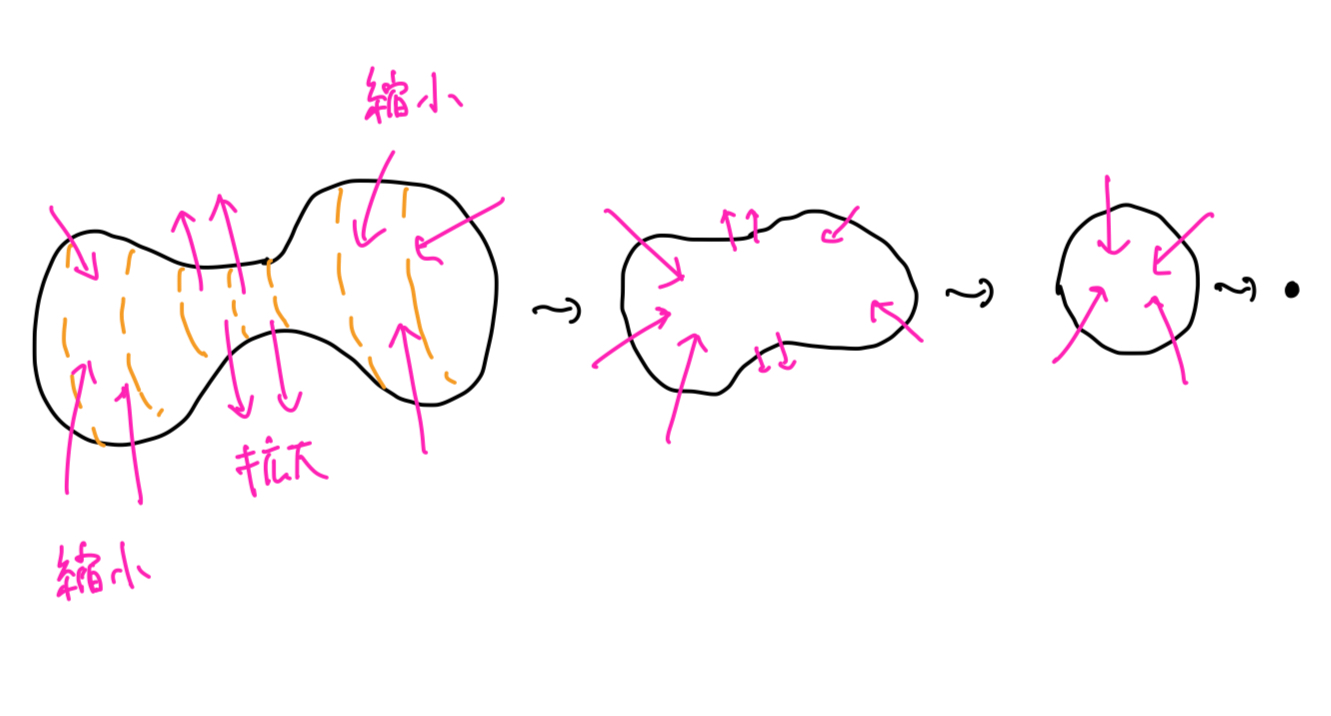ダンベル型の曲面をリッチフローで流す

この例から予想できるように，リッチフローが多様体の曲率をなだらかに"均す"ことを期待できる．まずはその性質を説明するための準備をしよう．

PDEの視点から

ここでリッチフローの偏微分方程式(PDE)としての性質をサッと紹介しよう．次章でここで紹介した性質からの帰結を紹介するので，PDEについて知らない読者はそこまでは適当に読み流してもらって構わない．

リッチフローの方程式(RF)に戻ろう．左辺の$\Ric(g)$という項が謎に見えるかもしれないが，実は$\Ric: g \mapsto \Ric(g)$という作用素は，2階の微分作用素と見ることが出来る．これはレビチビタ接続とリッチ曲率の局所表示を思い出してみると分かる．特に，調和座標系においては次のような局所表示が得られる：
$$\Ric(g)=-\frac{1}{2}\Delta_g g_{ij}+(\text{lower order terms})$$
(ここで，$g$の成分$g_{ij}$のラプラシアンをとっている.(計量との両立性$\nabla g\equiv0$からの帰結である$(\Delta _g g) \equiv 0$と別物であることに注意．))

ここから，リッチフロー方程式(RF)が熱方程式に形として似ているPDEであることがわかる．実際後で紹介するように，リッチフローに対して熱方程式と似た性質(最大値原理，平滑化作用，短時間解の存在と一意性など)が成立する．

ここで注意するべき点として，ラプラシアンの定義($\Delta_g=g^{ij}\nabla_i\nabla_j $)からリッチフローは準線型方程式になり，また，退化放物型であることが確かめられる．この方程式の解析はクラシカルな熱方程式の解析よりはるかに複雑であることに留意しておきたい．

リッチフロー方程式の基本的な性質

リッチフロー方程式に対する基本的な性質を紹介しよう．いきなり多量の結果を証明なしで提示することになるが，そんなに気持ちが分からない部分があっても一旦気楽な気持ちで読み進めて，あとから気になったら見返すくらいで良いだろうと思う．
先ほど指摘した熱方程式との類似性から，種々の最大値(最小値)原理が従う．これについては変種が色々あるのだが，例えば次を紹介する．

このような最大値原理は次章で多少のデモンストレーションをするが，スカラー曲率や様々なテンソルの大きさを上から抑えるのに便利なものである．
また，熱に似た性質として次の微分評価を挙げる．

$|\mathrm{Rm}|$の増加速度も似たように抑える定理も存在することも補足しておこう．また，時間微分についても同様に評価できることが知られている．

方程式が退化している分解の存在は非自明なのだがdeTurckトリックというある種のゲージ固定のような操作を行い，結局退化していない準線型放物型方程式(RIcci-deTurckフロー)の初期値問題の可解性に帰着する，ということをする．
一意性については調和写像の理論を使ってこれも放物型方程式の一意性の話に帰着する，という流れで示す．
また，大域解の存在について次を挙げる．

例えば，3次元のダンベル(心の目で見て欲しい)を考えるとこれは有限時間で潰れてしまうことがわかる．この例については最後の章で軽く触れる．
定理が意味するところは，このような"潰れ"がない限りリッチフローは流れるということである．
爆発する曲率

リーマン面の一意化定理について

リーマン多様体上の"綺麗な"計量

前章でリッチフローの道具立てを紹介した．特に定理2 を振り返ると，初期計量$g_0$に対して曲率の上からのバウンド$|\mathrm{Rm}(g)|< K$は，ある時間の範囲で曲率の高階の微分の大きさ指数関数的に減少させる効果があることを見た．これが曲率を"均す"性質を表している．

曲率の微分$\nabla\Rm(g)$が空間全体で恒等的にゼロであるということは$\Rm(g)$が空間方向に一定であることを意味し，それは定曲率リーマン多様体であることを意味する．この，全体で曲がり方が均一であるリーマン多様体は，いわば非常に"綺麗な"形をした多様体と言え，例えば次の結果のような分類が知られている．

例えばLee,Cha,Sak等を参照．

ここから逆に，このように問いかけることもできる．

「多様体$M$が与えられた時に，それに定曲率計量を入れることはできるか．」
(図．S^nに曲率を色々入れたやつ)

ここで「曲率」といった時，断面曲率，リッチ曲率，スカラー曲率のどれをとっても興味深い問題になり，例えばスカラー定曲率の計量が多様体に入るかという問題については肯定的に解決された．(山辺の問題Yam)

リッチフローはこのような定曲率計量の存在問題を考えるための一つのアプローチである．任意に与えた計量$g_0$に対して，リッチフローの解が有限時間で爆発しないならば定理4からそれは$t\rightarrow \infty$であるいい計量$g_\infty$に収束することを期待できるのだ．

一意化定理について

リッチフローの考案者であるリチャードハミルトン(注. 物理学で有名なハミルトンとは別人．)は，二次元閉多様体の場合にリッチフローに"修正を入れた"方程式が実際に無限時間まで解を持ち，定曲率計量に収束することを示した：

normalized Ricci flow(訳すなら正規化されたリッチフローか...)については後で説明を与える．

これの帰結として，任意のコンパクトリーマン面上に定曲率計量入れることができるということが示される．古典的なリーマン面の一意化定理と違い，ノンコンパクトなリーマン面は扱えないものの，定理6は定曲率計量の存在を言うだけでなく，任意の計量をある定曲率計量に滑らかに変形する($C^\infty$ホモトピーを与える)自然な方法を提供していると言える．
コンパクトリーマン面

一意化定理の証明

ここでは，一意化定理のリッチフローの証明のスケッチを紹介する．

準備

normalized Ricci flowとは次の方程式の解を指す．
$$\dt{g}=-2\Ric(g)+\frac{2}{n}r g \tag{nRF'}$$
ここで，$r \coloneqq \dfrac{\int _M R dV_g}{\int _M dV_g}$
は平均スカラー曲率と呼ばれるもので，分子のスカラー曲率の多様体全体での積分を分母の多様体の体積$\mathrm{Vol}(M,g)=\int_M dV_g$で割った平均である．時間の変化に対する体積要素$dV_{g(t)}$の変化を計算すことにより，この正規化されたリッチフローにおいては体積$\mathrm{Vol}(M,g)$が時間変化しないことが確かめられる．また，(RF)の解$\bar{g}$と(nRF)の解$g$は時間依存する滑らかな関数$\psi(t)>0$を用いて$g(t)=\psi(t)\bar{g}(t)$と書けることが導かれる．

また，Gauss-Bonnetの定理の帰結から，向きづけ可能な閉曲面に対して平均曲率$r$はオイラー標数$\chi(M)$と次の関係にあることが分かる：
$$\int_M K dV_g=2\pi \chi(M)$$
故に$r$は時間によらない量であり，またスカラー曲率とガウス曲率の関係(1)と合わせて，(nRF')は二次元の場合に次のように書き換えられる．
$$\dt{g}=(r-R)g \tag{nRF}$$
二次元の場合の正規化されたリッチフロー方程式(nRF)の右辺は$g$のスカラー倍で与えられ,(nRF)の解は$g(t)=u(t)g(0)$という等角(Conformal)な発展をすることも，解析のしやすさの要因の一つである．

証明のスケッチ

まず，定理4からわかる十分条件をクリアするため，曲率$R$が爆発しないことを示したい．計算から，スカラー曲率$R$が次のような時間発展をすることが確かめられる．
$$\dt{R}=\Delta_g R+R(R-r)$$
これは反応拡散方程式と呼ばれる形の方程式である．この項のラプラシアンを無くした次の常微分方程式を考えてみる．
$$\dt{s}=s(s-r)$$
この解は$s_0=s(0)$,$r$の符号によって次のように解ける.
\begin{cases} s(t)=\dfrac{r}{(1-\dfrac{r}{s_0})e^{rt}} &\text{if } r\neq0, s_0\neq0\\ s(t)=\dfrac{s_0}{1-s_0t} &\text{if }r=0\\ s(t)=0 &\text{if }s_0=0 \end{cases}
特に，$s_0\leq \mathrm{min}\{0,r\}$の場合に，
$$s(t)-r\leq s_0-r$$
が成立することが計算できるだろう．
$s(t)=R_{min}(t)$に対し，$r\geq s(t)$が成立するのは定義から従い，最大値原理を使い，次の$R$の下からの評価を得る．

これで下からのバウンドが得られた．

上からのバウンドを見るために，次の方程式の解$f$を考える．
$$\Delta_g f =R-r$$
この方程式は常に可解なのだが，それは$\int_M(R-r)dV_g=0$であることと関数解析のフレドホルム理論から分かる．(多様体のコンパクト性から$M$上の調和関数は定数関数しか存在しないことに注意)

この関数$f$を曲面のポテンシャルと呼ぶ．この関数$f$も良い振る舞いをすることが知られており，実際
$$\dt{f}=\Delta_g f+rf$$
という発展をし，最大値原理から定数$C$を用いて
$$|f|\leq Ce^{rt}$$
のようにバウンドできることが従う．

この$f$を用いて次の量を考える．
$$H\coloneqq R-r+|\nabla_g f|^2$$
この量も次の不等式を満たすことが計算でき，
$$\dt{H}\leq \Delta_g H+rH$$
これと最大値原理から，定数$C=C(g(0))$に対して，
$$R-r\leq H\leq Ce^{rt}$$
という評価が得られる流れである．

筆者はこの$H$を考える自然さがあまりよくわかっておらず，全てを解決する謎関数だと理解している(モチベーションを知っている人がいたら教えてほしい)．幾何解析のこういった初等的な計算においては，最大値原理等の適応を妨げる邪魔な項を打ち消すための謎の量を導入するといったことはよくあることだが，こういった幾何学的な直感・自然さを超えた部分に計算でたどり着くことができると言った部分は幾何解析の面白い部分であり，難しい部分でもあると思われる．

また，$|f|$のバウンドを用いると，次の評価も得られる：

ここで，テンソルの間の順序を考えているが，これは対称行列に対して定まる順序関係の自然な一般化となるようなものを考えている．

さて，これと補題7を組み合わせることで，次のバウンドが得られる．

これより，二次元の場合，スカラー曲率$R$が高々指数関数的な増大しかしないということが分かる．特に，有限時間で曲率が発散するということは起こり得ない．
これより，定理4から，$t\in [0,\infty)$における時間大域解が存在することが従う．

$r\leq 0$の場合には，$R$やポテンシャル$f$の挙動を追うことで,$R-r$とその任意解の微分がバウンドされることを見ることができ，(nRF)の式を通じて計量$g(t)$のバウンドを見ることができる．ここから計量の一様収束$g(t)\rightarrow g_\infty$が言えて，Ascoli-Arzelaの定理を用いて高階の微分の収束も言え，最終的に収束が滑らかであること($C^\infty$位相での収束であること)が言える流れである．

$r>0$の場合，問題が一気に難しくなる．まず，$R$やその微分を収束するという戦略が通用しなくなるので，方針の転換がいる．それについて軽く話そう．
まず，$r>0$，つまり(Gauss Bonnetの定理より)$\chi(M)>0$とはどういう状況かを考える．向きづけ可能位相多様体はトポロジカルに種数$g$を用いて分類されていることは知られており，そのオイラー標数は
$$\chi(M)=2-2g$$
として計算される．つまり，$\chi(M)>0$ならば，多様体$M$が球$S^2$と微分同相であるとして計算して良い．(ここで$3$次元以下の位相多様体の微分構造の一意性を使った．)
この場合の重要な観察として，$S^2$上の(グラディエント)リッチソリトン(gradient Ricci soliton)という重要な自己相似解が，カノニカルな定曲率計量$g(t)\equiv \tilde{g}$しか存在しない，という事実がある．
そこで，グラディエントリッチソリトンを特徴付ける式
$$\mathcal{H(g(t))}=\mathrm{Hess}_{g}(f)-\frac{1}{2}\Delta_g fg\equiv 0$$
(ここで$\mathcal{H}$はtracelessへシアンという量である．)
を踏まえ，$\mathcal{H(g(t))}$という量が$t\rightarrow \infty$で消えるということを示すという方針をとる．その証明では曲面のエントロピーの単調性を利用したり，なかなか楽しい解析をして証明をするので，興味のある人はRFSやCKなどを参照してほしい．

3次元のケースと特異点

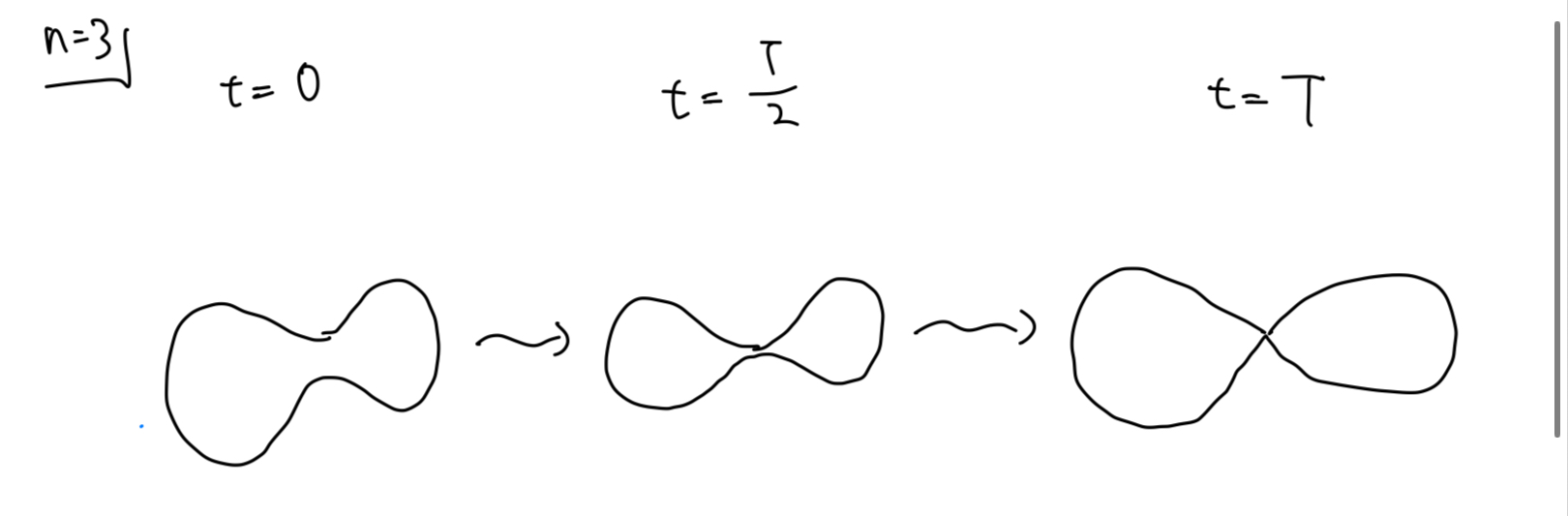
二次元の場合に，リッチフローの解が無限時間まで流れ，$t\rightarrow \infty$で定曲率計量に滑らかに収束することを見た．ところが，3次元以上になると，正規化したリッチフロー(体積を保つもの)でも実際に有限時間で爆発する次のようなダンベルような例が存在する．これは三次元球に計量を与えたものであるが心の眼で見てほしい．$K(e_i,e_j)$と書いたものは，ガウス曲率の高次元への一般化であり，断面曲率というものである．ダンベルの持ち手の部分で正曲率と負曲率が混在した結果，このようなちぎれが生じる．体積が明らかに変わっているのはご愛嬌と思ってもらってもかまわない．
$3$次元のダンベル
このような曲率の爆発する点を特異点といい，この極限の図形は潰れているので，もはや滑らかな多様体の枠組みで扱うことができない．
有名なミレニアム問題の一つである三次元ポアンカレ予想をより強いサーストンの幾何化予想の解決という形で解いたグレゴリーペレルマンは，特異点を解析する手法として手術つきリッチフローの理論を作ったことで知られている．
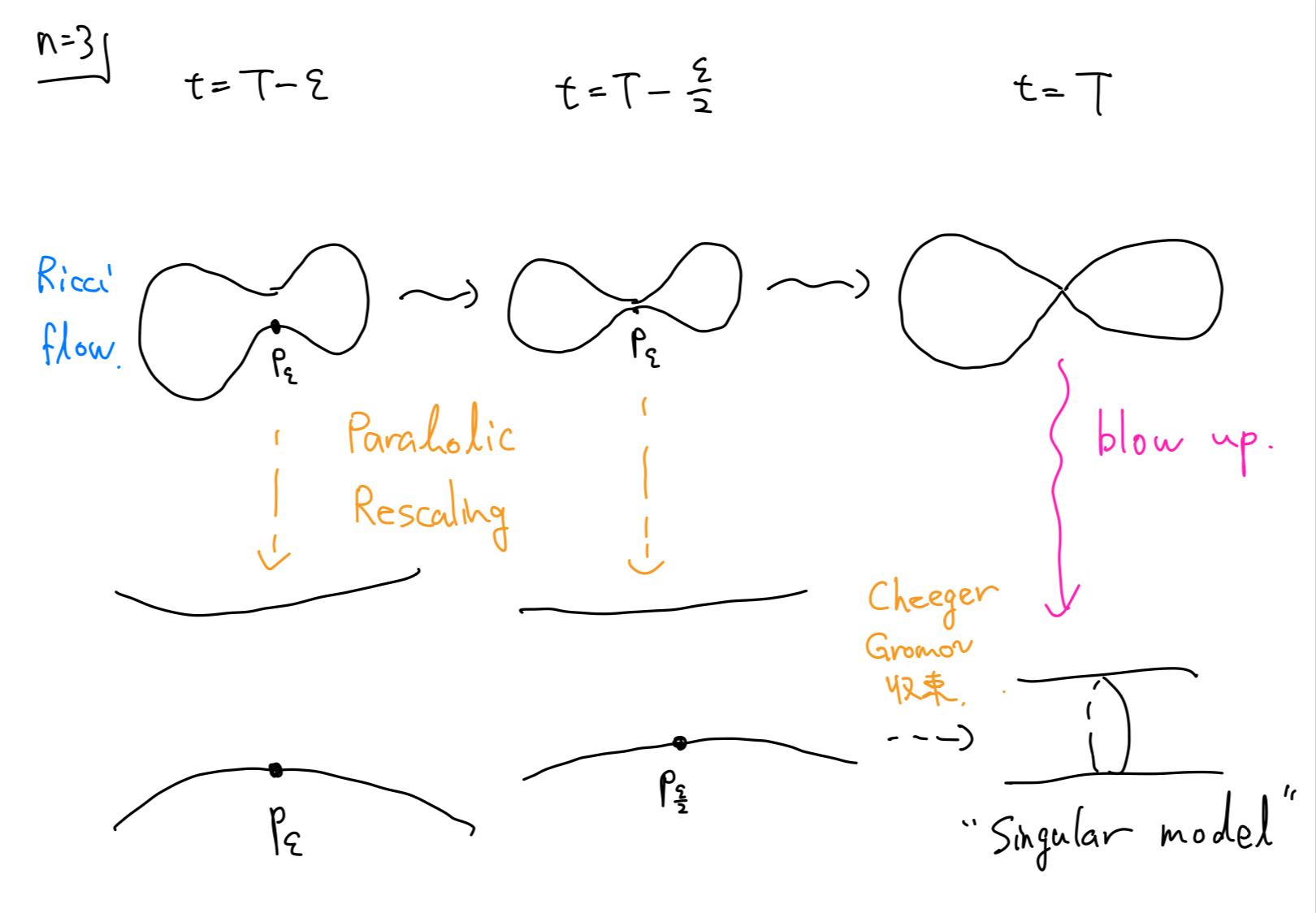リッチフローの特異点のブローアップ