高校までの極限の問題点とε-δ論法

高校までの極限は曖昧

数Ⅲを勉強した方なら、極限という概念については勉強したと思います。ここでは、高校における極限の定義を確認し、その問題について議論していきます。

高校における極限の定義

この定義は数Ⅲで習うものであり、覚えている人も多いと思います。また、この定義を感覚的に理解することはできるかもしれません。しかし、この定義には問題点があります。その問題点をこの次の節で解説していきます。

高校における極限の定義の問題点

この極限の最大の問題点は、「限りなく近づく」という表現の曖昧さです。「限りなく」とは具体的にどの程度近づければ良いのでしょうか。$a \pm 0.1$よりも近づければ良いのでしょうか、それとも$a \pm 0.01$程度にすれば良いのでしょうか。おそらく、この程度については高校の数学では習っていないことだと思います。

さらに、高校で数学が得意だった人は次のような疑問を抱くこともあったかもしれません。

なぜ、「限りなく近づく」はずなのに計算のときは代入しているのだろうか、それでは近づくというのはどういうことなのか。

本記事ではその疑問に対する答えにも迫っていこうと思っています。

厳密な極限とは

極限の定義

さっそくε-δ論法による厳密な収束の定義から説明していきます。

これが定義を厳密にした形です。難しいですね。筆者も数学を突き詰めようと思って、最初に勉強したのがこの概念で難しく感じた覚えがあります。でも、私はこの概念で数学がとても好きになったので、ぜひ理解してみてください。それでは解説していきます。

事前の注意

上記の定義では、$a$が無限大になることは考えていません。$a$が無限大になる場合も厳密に取り扱う方法がありますが、ここでは紹介しません。

イメージ

まずは、イメージから捉えていきます。大雑把なイメージは「近づけようと思えばいくらでも近づけることができる」ということです。言い換えれば、$f(x)$と$\alpha$の差($|f(x)-\alpha|$)を小さくしようと思えば、$x$と$a$の差($|x-a|$)を小さくすることによって、いくらでも小さくできるということです。

具体例

具体例を使って説明するので、イメージを参考に考えてみてください。例えば、$f(x)=x^2,a=2$とします。このとき、高校数学の知識を踏まえれば、$\alpha=4$に収束することがわかると思います。そこで、上記のイメージを使ってこのことを説明していきましょう。

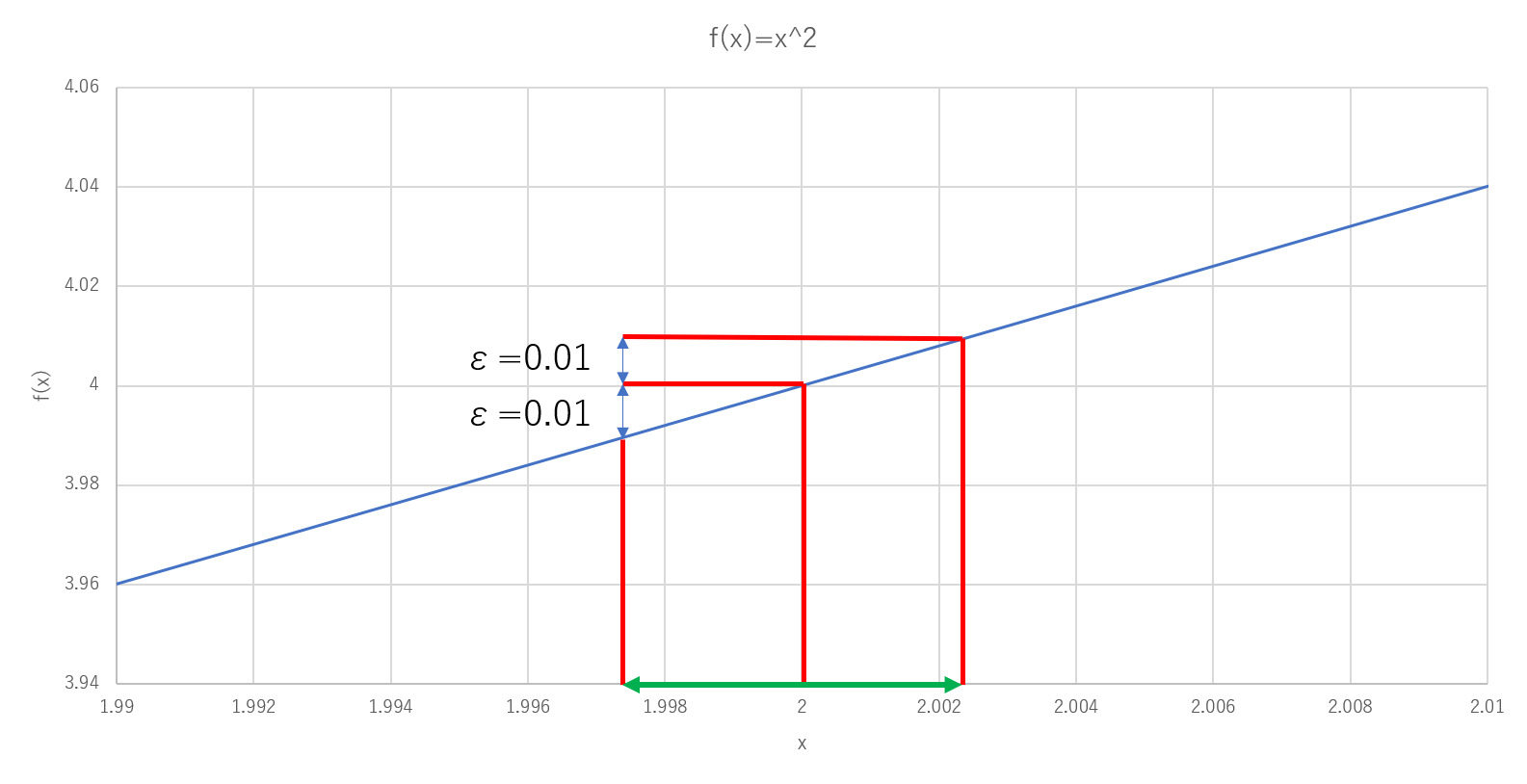収束の具体例

まず、$f(x)$と$\alpha$の差($|f(x)-\alpha|=|f(x)-4|$)を$\varepsilon = 0.01$よりも小さくするために、どの程度$x$を$a$に近づければ良いのか、つまり$|x-a|$を小さくすれば良いのかを考えます。$x=\sqrt{4.01}$もしくは$x=\sqrt{3.99}$とすれば、ちょうど$|f(x)-\alpha|=0.01$となります。つまり、$\sqrt{3.99} \lt x \lt \sqrt{4.01}$のときに$|f(x)-\alpha| \lt 0.01$となることが従います。また、$x$の条件を$|x-a|$を使って表すために以下のように式変形をしていきます。
$$ \begin{eqnarray} \sqrt{3.99} &\lt& x &\lt& \sqrt{4.01} \\ \sqrt{3.99} - 2 &\lt& x -2 &\lt& \sqrt{4.01} -2 \\ \sqrt{3.99} - 2 &\lt& x -2 &\lt& \sqrt{4.01} -2 \\ -0.002502\cdots &\lt& x -2 &\lt& 0.002498 \end{eqnarray} $$
となりますが、求めたいのは$|f(x)-\alpha| \lt 0.01$となるための十分条件であり、必要十分条件ではありません。言い換えれば、$|f(x)-\alpha| \lt 0.01$となるすべての$x$を含むような範囲を求める必要はなく、範囲内の$x$が必ず$|f(x)-\alpha| \lt 0.01$となるような範囲を求めればよいわけです。よって、$|x-2| \lt 0.002498 $が求めるべき範囲となります($|x-2| \lt 0.002498 $を満たせば$|x-2| \lt 0.002502 $を満たすことに注意)。

以上の議論をまとめれば、$f(x)$と$\alpha$の差が$0.01$よりも小さくするための範囲$|x-2| \lt 0.002498 $が存在したわけです。この関数の場合は同様に、$0.001$に対しては範囲$|x-2| \lt 0.00024998 $、$0.0001$に対しては範囲$|x-2| \lt 0.000024999 $が存在します。

また、同様に考えれば、どんなに小さい$\varepsilon > 0$を持ってきたとしても、$\delta = \sqrt{4+\varepsilon}-2$とすれば、$|x-2| \lt \delta $の中では必ず$|f(x)-\alpha| < \varepsilon $となるわけです。つまり、任意の$\varepsilon > 0$に対して、$\delta = \sqrt{4+\varepsilon}-2$が存在し、$|x-a|<\delta $を満たす任意の$x\in \mathbb{R}$で$|f(x)-\alpha|<\varepsilon$となったわけです。これが収束の定義そのものであるため、厳密に$ \displaystyle{\lim_{x \to 2}} f(x)=4$が示されたわけです。

どうでしょうか。この具体例を見た上で、定義の文章は理解できますでしょうか。$x=a$の取り扱いは次の連続関数の節でわかると思います。わからなかったらコメント欄にコメントお願いします。

余談

収束の証明する上で一番難しいのは$\delta$の見つけ方です。先程の例は簡単なものを用いたのでわかりやすかったですが、三角関数や指数関数、対数関数になってくると難易度がすこしあがります。ぜひ、ネットで調べて色々な関数の$\delta$の定め方を学んでみてください。

またこの記事は、極限の気持ちを理解するために書いているため説明しませんが、以下のような極限の性質も厳密に証明することができます(簡略化のために細かい条件は省略しています)。
$$ \displaystyle{\lim_{x \to a}} \left(f(x) + g(x) \right)= \displaystyle{\lim_{x \to a}} f(x) + \displaystyle{\lim_{x \to a}} g(x)$$

連続関数について

連続関数の定義

先程の例$f(x)=x^2$で考えると、$ \displaystyle{\lim_{x \to 2}} f(x)=4$でしたが、$f(2)=4 $あるため、$ \displaystyle{\lim_{x \to 2}} f(x) = f(2)$を満たしているので、$x=2$で連続です。また、先程の具体例と同様に考えれば、$a=2$に限らず、任意の点で$f(x)=x^2$は連続であることがわかります。すなわち、$f(x)=x^2$は連続関数であるわけです。

連続でない例を以下に出します。
$$ \begin{eqnarray} f(x) = \begin{cases} x^2 & ( x \neq 2 ) \\ 0 & ( x = 2 ) \end{cases} \end{eqnarray} $$
このように$f(x)$を定義すると、$ \displaystyle{\lim_{x \to 2}} f(x)=4$であることは先ほどと変わりません。これは収束の定義において$x \neq a = 2$となっているためです。しかし、$f(2)=0$であるため$x=2$で連続とは言えません。

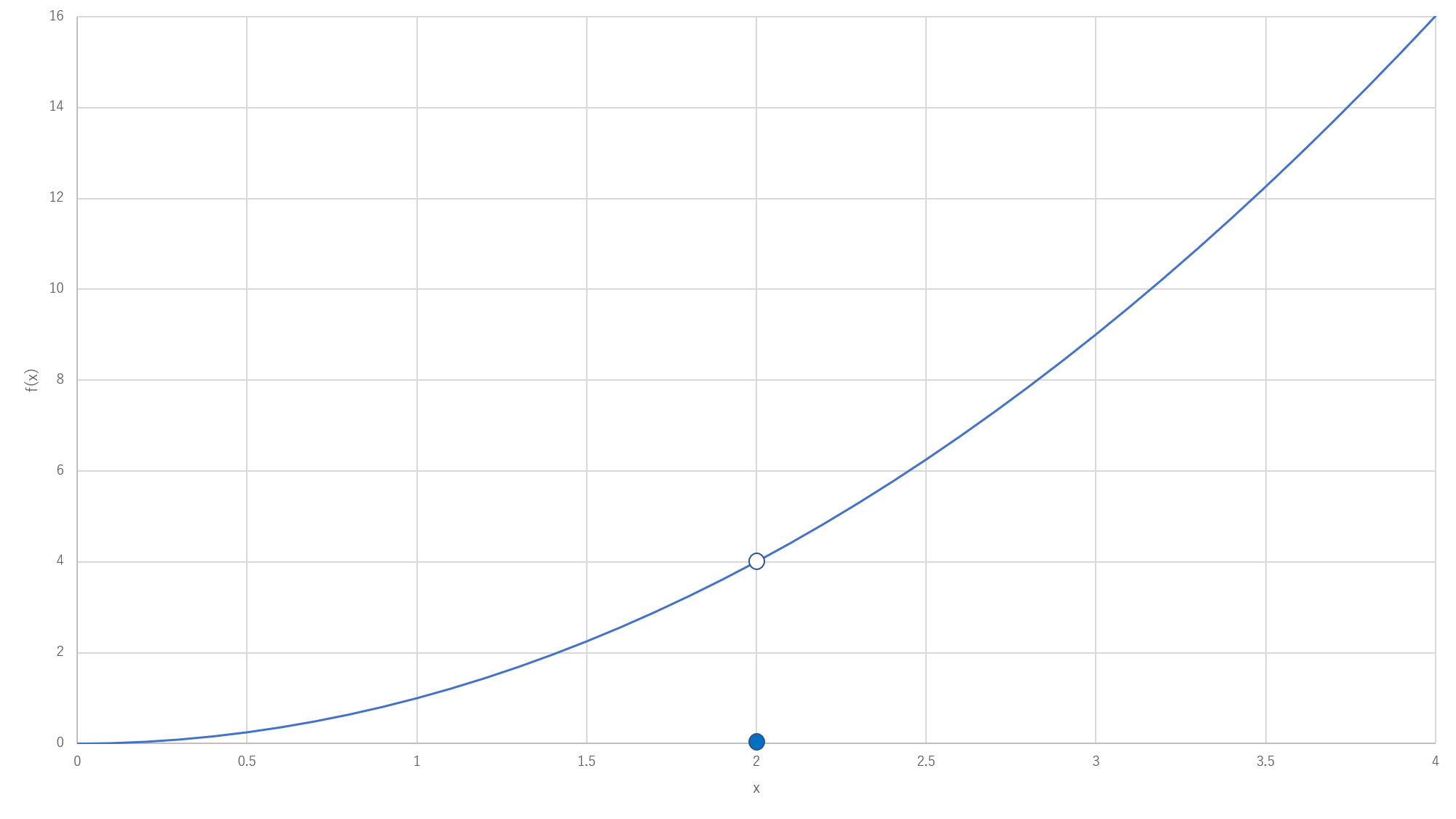連続でない関数のグラフ

上記に示したグラフを見てもらえばわかる思いますが、連続でない関数は途中で途切れている関数です。

冒頭の疑問について

ここで先程の疑問について考えていきます。

なぜ、「限りなく近づく」はずなのに計算のときは代入しているのだろうか、それでは近づくというのはどういうことなのか。

結論から言うと、高校に出てくる関数のほぼ全てが連続関数だからです。すなわち、高校で出てくる関数はほぼ全てが先程の具体例と同じように厳密に、定義域の任意の$a$に対して、$ \displaystyle{\lim_{x \to a}} f(x)=f(a)$になることが示せるということです。

おわりに

いかがだったでしょうか。高校の定義を厳密にしていくのは、難しさが伴いますが、当たり前だと思っていた事実にきちんとした証明がつき、数学という学問の理論に美しさを味わうことができるでしょう。当たり前なものに対する厳密な証明に必要性を感じられなかった人もいたかもしれません。しかし、我々人類が新たな理論を創り出したり、科学を進歩させる上で、厳密に導き出された数学というのは、非常に強力な武器といえるでしょう。では、すばらしい数学ライフを！！