自作問題No.13

問題

単行本「ご注文はうさぎですか？」第6巻9話「BREAK RABBIT BANK!」p81においてココア、チノ、リゼ、千夜、シャロ、マヤ、メグの7人が青山氏の提案により「シークレットサンタ」を行っていた。(「ご注文はうさぎですか？BLOOM」11羽でも同様)「シークレットサンタ」とは、主にアメリカ、オーストラリアなどの欧米諸国で行われる伝統的なプレゼント交換の方法である。実際に彼女たちが行った手順を操作$A,B,C$として以下に示す。

$A$.7人の名前をそれぞれ書いたくじ7本を中を見ずに全員で一度に引く。
　$B$.くじを開き、一人でも自分の名前を選んだ場合、もう一度全員で引き直す。
　$C$.選んだ相手に渡すプレゼントを各々考え、後日一人ずつ順に渡す。

そして本編では以下の図のような関係でサンタが1回で決定した。ただし、数字は後に明かされた順番であり、矢印の始点から終点の人へプレゼントが渡されたものとする。また、矢印は左、右のどちらも時計回りであり、$A,B$を人物として$A \rightarrow B$となっているとき、これを「$B$のサンタが$A$である」と表現することとする。

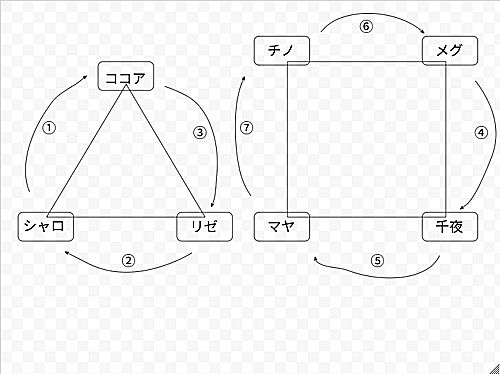サンタの関係図

次の問に答えよ。ただし、(1)以外は前問すべての状況が既知であるとして時系列順に考え、条件付き確率で求めよ。

(1)操作$B$が行われない確率を求めよ。

(2)ココアのサンタがシャロになる確率を求めよ。

(3)シャロのサンタがリゼになる確率を求めよ。

(4)リゼのサンタがココアになる確率を求めよ。

(5)千夜のサンタがメグになる確率を求めよ。

(6)マヤのサンタが千夜になる確率を求めよ。

そして、最後にメグのサンタがチノになる確率と、チノのサンタがマヤになる確率はともに$1$となる。