初等幾何における特殊な相似変換
記事の内容
初等幾何においてしばしば重要視される相似変換について、優美だなと思ったものを取り上げます。エレガントな議論には学べることが多いです。勉強とは時間をかけて一つ一つ解読していくものだけ、というのでは飽き足ります。綺麗な問題を実際に解いてみて、あるいは解き方を参照して、得るものがあった瞬間が一番楽しい。(とはいえ前者のようなある種みみっちいやり方は不可欠であり、より莫大な効用があるので、筆者はそれを愛せず大いに困っている)
Yahoo知恵袋で少し前に拾った問題
$∠A=90°$である直角三角形$ABC$がおいて、$AB$を介して点$C$と対称な点を点$C´$、点$A$から$BC$へ下した垂線の足を点$H$とする。$AH$の中点$K$をとると、$BK\perp HC´$が成り立つ事を示せ。
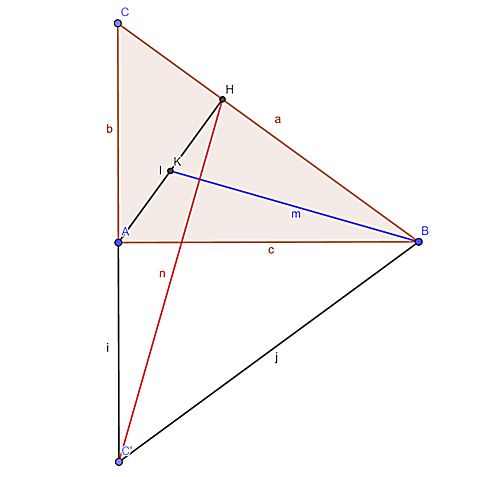 添付図
添付図
平面幾何の良問。基本的かつ沼る人は沼るという意味で。命題や構図が単純なだけにその傾向が強い。競技数学を意識している人も楽しめるんじゃないか
以下の添付図参照。また、$∽$は相似の記号であることに注意。
点$C´$から$BC$へ下した垂線の足を点$I$、また点$A$から$ID$へ下した垂線の足を点$E$とする。$AH\parallel DI$より点$H$は$CI$の中点であり、また$AE\parallel CI$より$HD$が$AE$の中点$L$を通ることが分かる。四角形$AEIH$が長方形である事は明らかであるが、この時$▲AHE∽▲HAB$に注目すると、点$L,K$はそれぞれこの相似において対応する辺の中点なので、この二点を注視すれば$▲AHL∽▲HBK$が言えるはずなのである。これにより$∠AHL+∠HKB= 90°$ を示すことができるので、題意が示せる。
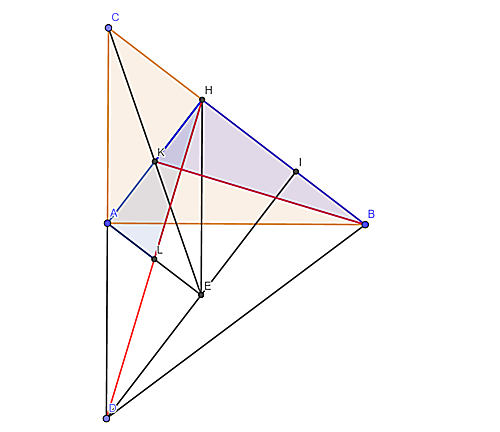 添付図
添付図
教訓があるとすれば~中点は中点で相殺すべし~だろう。「$▲AHE∽▲HBA$$ \Longrightarrow $$▲AHL∽▲FBK$」の言い換えが印象的だったと思う。ちなみに同様にすれば$▲HBA∽▲ICD$を示すだけで良いのだけど、あえて思考過程のまま書き起こした。こっちの方が図形が綺麗。
2017年JMO本選第3番
三角形$ABC$があり、その外心を$O$とする。3点$A,B,C$から対辺に下した垂線の足をそれぞれ$D,E,F$とし、さらに$BC$の中点を$M$とする。直線$AD$と直線$EF$の交点を$X$、直線$AO$と$BC$の交点を$Y$、線分$XY$の中点を$Z$とする。この時$A,Z, M$が同一直線上にあることを示せ。(句読点の表記を除いて、原文ママ)
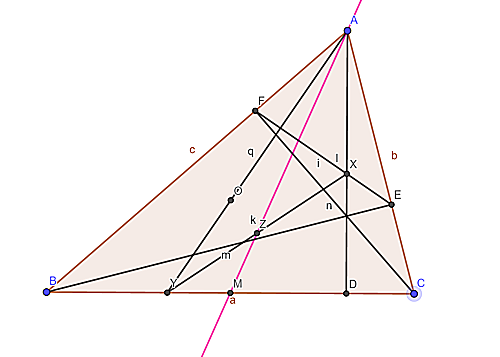 添付図
添付図
難易度がちょっと跳ね上がったかもしれないが、有名な構図で綺麗な相似関係がでてくる。問題は載せておくが、解説は控えることにする(意味ありげにいうがおそらく支障はないので面倒なだけである)
解説が気になる人は数学オリンピック財団監修の「数学オリンピック2014-2018」を参考にされたし。もともとその本にあった解説です。(あるいは気が向けば書くかもしれないが、想像もできないプルプルプル)
この問題はメネラウスの定理の逆を使う方針でやや強引に解くこともできる。これも初等の範囲内といえると思うが、相似を使う方が賢い。
2017年春合宿2番
この問題もずっと難易度が跳ね上がってしまうので、回転相似をうまく使った同一円の議論が出てくる、その部分だけかいつまんで紹介しよう。初見で解きたい人は見ない方がいい
三角形$ABC$は$AB \neq AC$をみたす。三角形$ABC$の外接円を$ \Gamma $とし、内心を$I$とする。$M$を$BC$の中点とし、$I$から$BC$へ下した垂線の足を$D$とする。$I$を通り直線$AI$に垂直な直線は辺$AB$と辺$AC$にそれぞれ$F$と$E$で交わる。三角形$AEF$の外接円と$ \Gamma $の交点のうち、$A$でない方を$X$とする。このとき、直線$XD$と直線$AM$は$ \Gamma $上で交わる事を示せ。
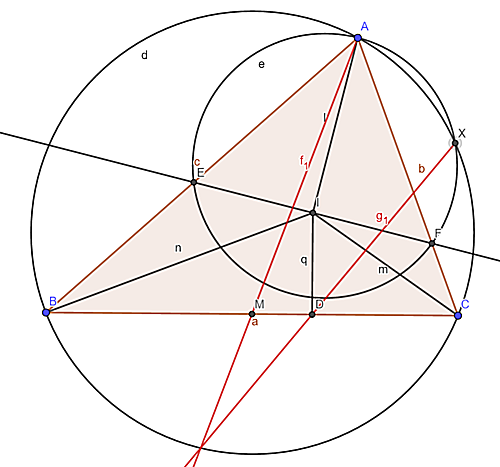 添付図
添付図
本題
この構図では以下の命題が成り立つ。
$\stackrel{\huge\frown}{BC}$のうち$A$を含めない方の中点を$N$、直線$EF$と直線$BC$の交点を点$G$とすると、五点$X,I,M,N,G$は同一円周上にある。
$A,I,N$が同一直線上にあり、$∠NIG=∠NMG=90°$より円周角の定理の逆から四点$I,M,N,G$が同一円周上にあることは確かめられるので、四点$G,X,I,M$が同一円周上にあると分かれば題意が示せる。円周角の定理より$∠EAF=∠EXF,∠XEF=∠XAF$。同様に$∠BAC=∠BXC,∠XBC=∠XAC$。よって$∠EXF=∠BXC,∠XEF=∠XAC$より$▲XEF∽▲XBC$。
ここで、二つの三角形において点$I,M$はそれぞれ辺$EF,BC$の中点なので、二点は対応している。よって$▲XIF∽▲XMC$であり、$∠XIF=∠XMC$を得る。円周角の定理の逆より四点$X,I,M,G$が同一円周上にある。以上より題意が示せた。
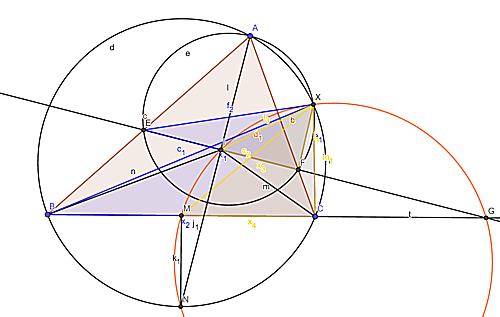 添付図
添付図
先に挙げた問題と似た議論がでてきた。相似と同一円の議論は相性がいいので、要チェックでなきにしもあらず。
元の問題はこの命題が一つ目のステップとなる。興味がある人は考えてみてはいかがか。
回転相似について
もう少し発展した議論をすれば
$▲XEF∽▲XBC$から三角形$AEF$の外接円と$ \Gamma$という二つの円の$X$を中心とした回転相似を考えると$N$が直線$AI$と三角形$AEF$の外接円の交点に移るので、その点が$AN$上にあることから$∠XIN=∠XMN$が言える。これにより題意を示すという方法もある。こちらも重要な相似変換の考え方だろう。
今回のような外接円の交点が出てくる構図では回転相似が多く出てくることがある。あるいは外接円と外接円の交点をとって回転相似を出現させて解ける問題も多い。というのも、回転相似とある円と円の交点は密接に関係しているのである。
そのことについてはまた別の機会に取り上げる。寒くてたまらない
おわりに
相似や合同などによる議論は有用ではあるが万能ではないので、もしそれだけで解ける問題ならたぶん難問ではありません。その時々に優美でエレガントなアイデアを探求することこそ初等幾何の醍醐味だと思います。
それらはただのひらめきや独特の感性によるものとは限りません。僕にとって幾何学に肝要なのは、緻密にも大まかにも重要な独自の因子を拾い集められる、幾何学的な美しさにより沿った探求ができる好奇心によって伴う第六感なのだと思います。
後述:誤字の指摘がありました。ご迷惑をおかけして申し訳ない。感謝いたします。こういうご指摘はとてもありがたいので、ビシバシお願いします。。