20201231（大晦日）と20210101（元日）が素数なのは珍しいらしいので、Juliaで色々調べてみた。

経緯など

「20201231と20210101は素数で、大晦日・元日ともに素数なのは珍しい」とSNSで読んだので、くわしく調べてみることにしました。
プログラミングの練習結果という感じで、あまり数学っぽさはない記事なのですが、折角の年末年始ということで、お許し頂ければと思います。

以下の計算結果は、私なりに確認はしていますが、素人プログラミングなので、間違いを含む可能性もあります。もしも真面目に参照する場合は、ご自身でもご確認頂ければと思います。

Juliaで計算したよ

丸美屋の麻婆豆腐よりを作るよりも環境構築が簡単なことで有名な Julia で計算しました。「何もしてないのにパソコン壊れた」と四六時中思ってる私が使えているので、良い時代になりましたね。

2020年の次は2029年、その次は2161年

西暦1年～3000年までで、大晦日・元日ともに素数の日は以下です。

41231と50101
1031231と1040101
1601231と1610101
1901231と1910101
2111231と2120101
2711231と2720101
3041231と3050101
3461231と3470101
3671231と3680101
3761231と3770101
4511231と4520101
4751231と4760101
5021231と5030101
5501231と5510101
5861231と5870101
6491231と6500101
7361231と7370101
7991231と8000101
8171231と8180101
8741231と8750101
9371231と9380101
10001231と10010101
10181231と10190101
10511231と10520101
10841231と10850101
11261231と11270101
11531231と11540101
11591231と11600101
11651231と11660101
11861231と11870101
11981231と11990101
12371231と12380101
14681231と14690101
15131231と15140101
15551231と15560101
16001231と16010101
16211231と16220101
17471231と17480101
18101231と18110101
18281231と18290101
18911231と18920101
19301231と19310101
19721231と19730101
19781231と19790101
19871231と19880101
20201231と20210101
20291231と20300101
21611231と21620101
23831231と23840101
24131231と24140101
24371231と24380101
25331231と25340101
25811231と25820101
26021231と26030101
26501231と26510101
26891231と26900101
27761231と27770101
29321231と29330101

計58回です。
2020年の次は2029年なので、すぐ来ますが、その次は2161年なので、たぶん経験できないと思います。

$10^4$年までだと、計164回です。

$10^5$年までだと、計1168回です。

$10^6$年までだと、計9086回です。

最大経験回数は6回（西暦1～3000年に生まれた人が80年～110年生きる場合）

人生で、大晦日・元日ともに素数の年を経験できる回数を調べてみました。

西暦1年～3000年に生まれた人を対象としています。

西暦$i$年生まれで、$M$年生きる場合、$i$年12月31日～$(i+M)$年1月1日を経験できるとして、計算しました。

• 70年生きる場合：5回が最大、0回が最小

• 80年生きる場合：6回が最大、0回が最小

• 90年生きる場合：6回が最大、0回が最小

• 100年生きる場合：6回が最大、0回が最小

• 110年生きる場合：6回が最大、0回が最小

• 120年生きる場合：7回が最大、0回が最小

• 密集ポイント
  10841231と10850101
  11261231と11270101
  11531231と11540101
  11591231と11600101
  11651231と11660101
  11861231と11870101
  11981231と11990101
  12371231と12380101

• 直近の密集ポイント
  19301231と19310101
  19721231と19730101
  19781231と19790101
  19871231と19880101
  20201231と20210101
  20291231と20300101

1930年生まれの方は6回経験できるかもしれません。

逆に経験回数が少ないケースについては、例えば、2031年生まれの場合は、次回が130年後の2161年なので、一度も経験できなさそうです（寿命は延びるかもしれませんが）。

2161年の次は2383年なので、こちらは222年も空いています。

大晦日・元日素数砂漠

大晦日・元日ともに素数の年の間隔を調べてみました。

大晦日・元日ともに素数の年の西暦を$N$、$N$の次に大晦日・元日ともに素数となる年の西暦を$M$として、$(N,M,M-N)$の形で記載しています。

※$N,M$は大晦日の西暦に合わせています。

3000年まで

$M-N$が小さものから順に記載しています。
(1159, 1165, 6)
(1972, 1978, 6)
(367, 376, 9)
(1978, 1987, 9)
(2020, 2029, 9)
(1186, 1198, 12)
(799, 817, 18)
(1000, 1018, 18)
(1810, 1828, 18)
(190, 211, 21)
(346, 367, 21)
(1165, 1186, 21)
(1600, 1621, 21)
(2581, 2602, 21)
(451, 475, 24)
(2413, 2437, 24)
(475, 502, 27)
(1126, 1153, 27)
(160, 190, 30)
(2383, 2413, 30)
(271, 304, 33)
(1018, 1051, 33)
(1051, 1084, 33)
(1987, 2020, 33)
(550, 586, 36)
(1198, 1237, 39)
(1891, 1930, 39)
(2650, 2689, 39)
(304, 346, 42)
(1084, 1126, 42)
(1513, 1555, 42)
(1930, 1972, 42)
(1468, 1513, 45)
(1555, 1600, 45)
(502, 550, 48)
(2533, 2581, 48)
(2602, 2650, 48)
(103, 160, 57)
(817, 874, 57)
(211, 271, 60)
(586, 649, 63)
(736, 799, 63)
(874, 937, 63)
(937, 1000, 63)
(1747, 1810, 63)
(1828, 1891, 63)
(376, 451, 75)
(649, 736, 87)
(2689, 2776, 87)
(2437, 2533, 96)
(4, 103, 99)
(1621, 1747, 126)
(2029, 2161, 132)
(2776, 2932, 156)
(2161, 2383, 222)
(1237, 1468, 231)

間隔の最小は(1159, 1165, 6)(1972, 1978, 6)

間隔の最大は(1237, 1468, 231)

間隔の平均値：51.36842105263158

間隔の中央値：39.0

間隔の最頻値：63

標準偏差：46.26809745499876

以下は1刻みでヒストグラムを描いたものです。
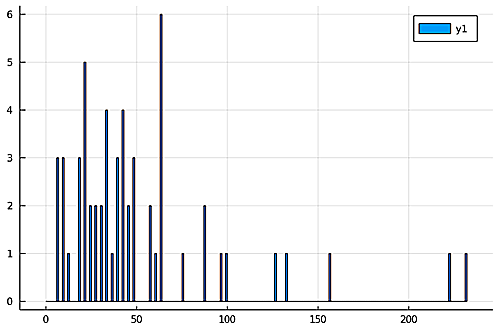3000年間隔

10^4年まで

間隔最小は(3685, 3688, 3), (8653, 8656, 3)

間隔最大は(3727, 4000, 273)

間隔の平均値：61.17791411042945

間隔の中央値：42.0

間隔の最頻値：33

標準偏差：55.92995180761789

以下は1刻みでヒストグラムを描いたものです。
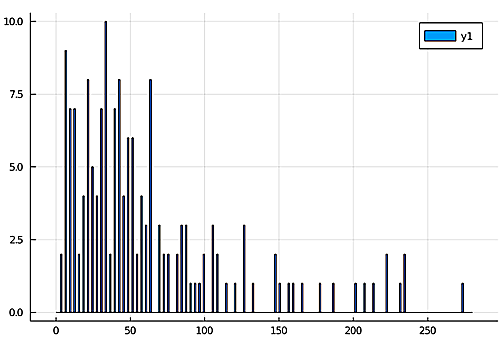10^4年間隔

10^5年まで

間隔最小は(3685, 3688, 3), (8653, 8656, 3), (12862, 12865, 3), (17659, 17662, 3), (18040, 18043, 3), (26836, 26839, 3), (29737, 29740, 3), (31489, 31492, 3), (32320, 32323, 3), (34168, 34171, 3), (45748, 45751, 3), (49558, 49561, 3), (59578, 59581, 3), (65551, 65554, 3), (68584, 68587, 3), (72892, 72895, 3), (73783, 73786, 3), (77593, 77596, 3), (77710, 77713, 3), (81649, 81652, 3), (83749, 83752, 3), (92380, 92383, 3), (95728, 95731, 3)

間隔最大は(73267, 73783, 516)

間隔の平均値：85.52956298200515

間隔の中央値：60.0

間隔の最頻値：33

標準偏差：80.43406433247306

以下は1刻みでヒストグラムを描いたものです。
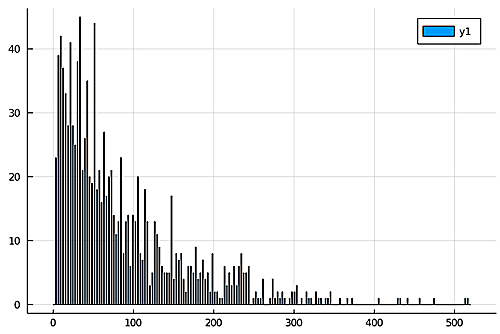10^5年間隔

10^6年まで

間隔最小は(990274, 990277, 3)など（193例あり）

間隔最大は(630124, 631117, 993)

間隔の平均値：110.04468904788112

間隔の中央値：75.0

間隔の最頻値：33

標準偏差：108.13906430000286

以下は1刻みでヒストグラムを描いたものです。
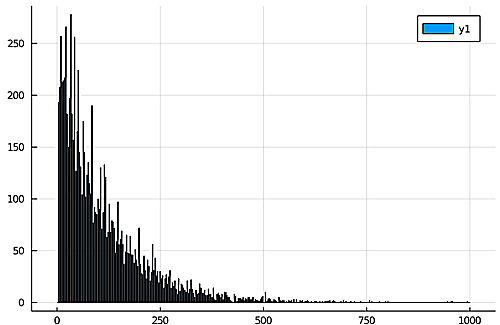10^6年間隔

※10^7のときも最頻値33でした。

分布の様子

大晦日・元日ともに素数の年が、どのように増えていくかを調べてみました。

西暦$x$年までに、大晦日・元日ともに素数の年が何回あったかをグラフにし（ 素数定理 の$\pi(x)$のような感じ）、一次多項式による近似（ CurvFit を使用）をしてみました。

• $x$軸：西暦。大晦日の西暦に合わせています。
• $y$軸：西暦$1$～$x$年までの間（$x$年を含む）に、大晦日・元日ともに素数の年があった回数。例えば「20201231・20210101」のセットで1回とカウント。

3000年まで

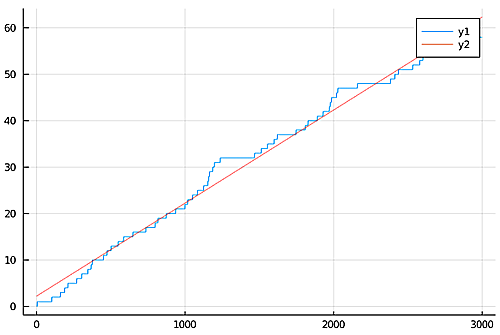3000年
直線の方程式：$$2.222208736245482 + 0.020037848226427582x$$

10^4年まで

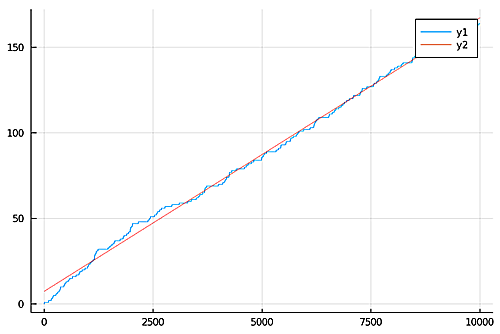10^4年
直線の方程式：$$7.391112331233181 + 0.015993898143938975x$$

10^5年まで

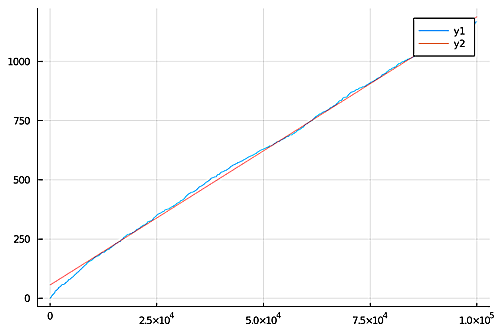10^5年
直線の方程式：$$55.95680851948376 + 0.01133425168709343x$$

10^6年まで

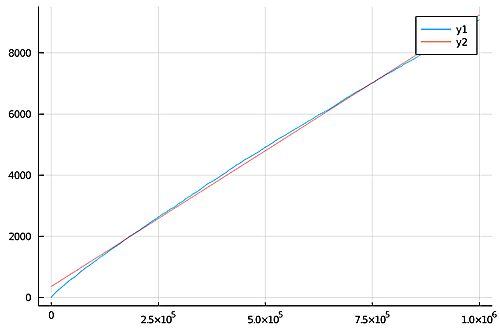10^6年
直線の方程式：$$360.9829038979336 + 0.008878800643403162x$$

感想

さすがは素数なので「どんな風に出現するか」が予測できない感じがしました。

また、こういった条件のある素数の組が、無限に存在するのか否かということにも関心がわいてきました（今回のケースって、証明できるんですかね…？）。

素数、なんもわからん！