【詳しい人は】クロススイッチ問題【教えてくれ】
今回は、僕が『クロススイッチ問題』と(勝手に)呼んでいるものについてお話しします。
(分量:10分程度)
ゲーム 『クロススイッチ』
ルールは簡単!
ここに、いくつかのスイッチが上下左右につながりあっています。
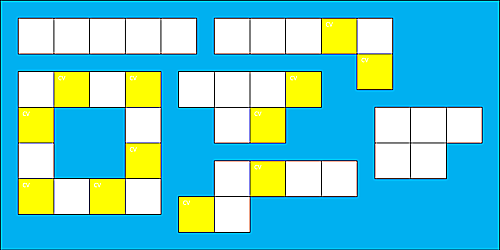 スイッチ図いろいろ
スイッチ図いろいろ
スイッチは、【on】の状態だとスイッチ自身が光ります。
そして、すべてのスイッチは手動で【on】と【off】を切り替えることができますが、あるスイッチを押すとそのスイッチと上下左右で隣り合っているスイッチもすべて切り替わります。
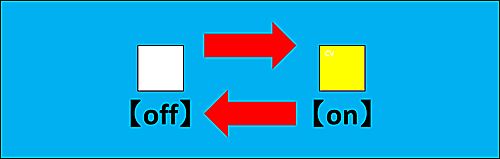 オンオフ説明図
オンオフ説明図
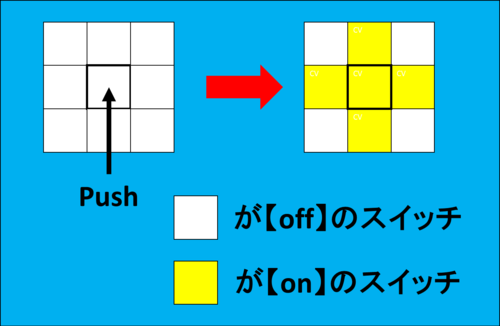 スイッチ切り替え表示
スイッチ切り替え表示
では目の前にあるスイッチ達の状態から、いくつかを切り替えて、すべてが【on】の状態にすることができるでしょうか?
まずは例題で、確認と腕試しといきましょう。
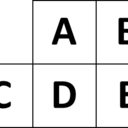
例題
 4-直線スイッチの図
4-直線スイッチの図
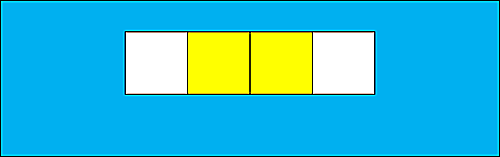
これは、スイッチが4個横並びになっている様子を表しています。
そして、真ん中にある二つの黄色くなっているのはスイッチが光っている、つまりこれらのスイッチが【on】の状態になっており、左右の端それぞれにある白くなっているのは、スイッチが【off】の状態を表しています。
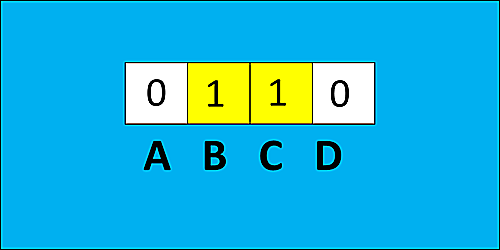
ここで、この図の左端のスイッチからA,B,C,Dと記号をつけ、【on】のスイッチを1、【off】のスイッチを0と数字で表すとすると、上の図は
A:0 , B:1 , C:1 , D:0
となります。
 4-直線スイッチの図(記号あり)
4-直線スイッチの図(記号あり)
これを縮めて、 0110 と表すことにしましょう。
これで上の図の様子を0110と数字の列で表すことができました。これからはこの数列を使っていきましょう!
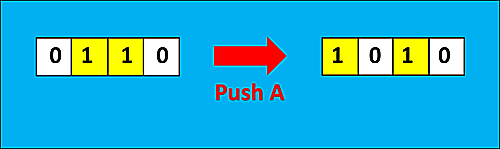
ではこれからスイッチを押していきます。まず一番左、Aのスイッチを押すと、スイッチ達には次のような変化が起こります。
A:0 → A:1
B:1 → B:0
まず、押されたAのスイッチ自身が切り替わり、【off】から【on】になりました。そして、Aと隣り合っているBのスイッチも切り替わり、【on】から【off】となりました。C,DのスイッチはAのスイッチとは隣り合っていないので、変化はありません。
この変化により、スイッチ達の状態が、0110 から1010に変わりました。
ここで一つ用語を定義します。先ほどAのスイッチを押しましたが、この操作のことを
Push A
と呼ぶことにします。同じように、B,C,Dのスイッチを押す操作をそれぞれ、
Push B , Push C , Push D
と呼びます。さらに、Aのスイッチを押したあとに、Bのスイッチを押すこと、つまりPush A, Push B の操作を続けて行うことを、
Push AB
と呼ぶことにしましょう。
この用語を使うと、先ほどはPush Aの操作により、スイッチ達は0110から1010に変化したといえます。
 4-直線スイッチ、Push A
4-直線スイッチ、Push A
さて、今のスイッチ達の状態は1010です。ここでPush Cを行うことで、スイッチ達は1101に変化します。
Push Cにより、
C:1 → C:0 となります。
また、Cと隣り合っているスイッチはB,Dの2つで、
B:0 → B:1
D:1 → D:0 と切り替わります。
スイッチAはスイッチCとは隣り合っていないので、この操作では変化しません。
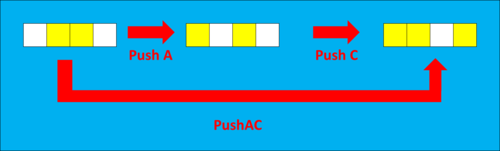
ここまでで、Push A,Push Cと続けて行いましたが、これらの操作をまとめて、Push ACと呼ぶのでした。つまり、Push AC により、スイッチ達は、0110から1101に変化したといえます。
 4-直線スイッチ、Push A、Push C
4-直線スイッチ、Push A、Push C
このまま、他のスイッチも押してみて、すべてのスイッチを光らせてみましょう!Push AC と押して、0110から1101となりました。ここから、どのスイッチを押せばいいでしょうか?
・
・
・
・
解答
Push B より、A,B,Cのスイッチが切り替わり、
1101 → 0011
Push A より、A,Bのスイッチが切り替わり、
0011 → 1111
1はスイッチが【on】の状態であることを表していましたので、1111はすべてのスイッチが【on】、つまりすべてのスイッチが光った!ということになります。
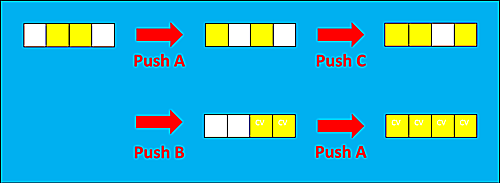
ここまでをまとめると、スイッチははじめ0110の状態でしたが、
スイッチをA,C,B,Aの順に押すと(すなわち、Push ACBA と操作すると)、1111となりスイッチをすべて光らすことができました。
 4-直線スイッチ、Push A、Push C、Push B,Push A
4-直線スイッチ、Push A、Push C、Push B,Push A
ここで問題
次は、上とは違う図の問題に挑戦してみましょう!
以下の二つの図のスイッチ達は、どのように押せばすべて光らせることができるでしょうか?
(1)
 8-ループ図
8-ループ図
(2)
 1-直線、4-ループ図
1-直線、4-ループ図
『クロススイッチ問題』への準備
ここまではパズルの問題でしたが、これから数学らしい議論をしていきます。
まずはPush の性質から見てみましょう。
Push 1 をどのスイッチも押さない操作、とする
Push A = Push B とは、Push A の操作を行ったときのスイッチ達の切り替わり方と、Push B の操作を行ったときのものが同じ、ということを表す。
Push AA = Push 1
同じスイッチを2回押すと、そのスイッチ自身と、これとつながっているスイッチ達の各々が変化し、それ以外のスイッチは変化しません。
変化するスイッチはそれぞれ、
最初が1とすると、 1 → 0 → 1 と変化し、
最初が0とすると、 0 → 1 → 0 と変化します。
すなわち、スイッチを押す前と状態が変わらないので、どのスイッチも押さない操作と一致します。
よって、この操作を行ったときの変化は、全くスイッチを押さない操作と一緒になるので、この命題が成立します。
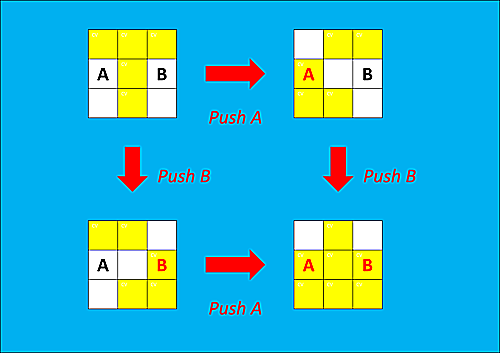
Push AB = Push BA
 Push AB=Push BA
Push AB=Push BA
この命題は、スイッチ達を次の4つのグループに分けて考えていきます。
〈1〉スイッチA,Bのどちらともつながっていないスイッチのグループ
〈2〉スイッチAとは隣り合っているが、Bとは隣り合っていないスイッチ
のグループ
〈3〉スイッチBとは隣り合っているが、Aとは隣り合っていないスイッチ
のグループ
〈4〉スイッチA,Bのどちらとも隣り合っているスイッチのグループ
〈1〉スイッチA,Bのどちらともつながっていないスイッチのグループ
このグループのスイッチ達はA,Bのどちらを押しても変化しないので、スイッチをどちらから押しても状態が変わることはない。
〈2〉スイッチAとは隣り合っているが、
Bとは隣り合っていないスイッチのグループ
このグループのスイッチ達は、Push A によって状態が切り替わるが、Push Bでは変化しないので、Push ABとPush BA のどちらの操作を行ってもスイッチAとつながっているスイッチが切り替わる変化となる。
〈3〉スイッチBとは隣り合っているが、
Aとは隣り合っていないスイッチのグループ
このグループについては、〈2〉のグループと同様に、Push ABとPush BAで同じ変化となる。
〈4〉スイッチA,Bのどちらとも隣り合っているスイッチのグループ
Push AB の操作を行うと、このグループにいるスイッチ達は、各々2回切り替わる。よってスイッチを押す前から変化しない。
Push BA の操作も同様に変化しない。
したがって、Push AB と Push BA では同じ変化をするといえる。
すべてのスイッチは、上の4つのグループのいずれかに必ず属しており、どのグループに属していてもPush AB,Push BA の2つの操作の切り替わり方は同じである。したがって、Push AB = Push BA.
Push A(BC) を Push A 、Push BC の順に操作すること、
Push (AB)C を Push AB 、 Push C の順に操作することとすると、
Push (AB)C = Push A(BC)
Push (AB)C は、Push AB , Push C と続けて操作することを表す。
すなわち、Push A , Push B , Push C と続けて操作することを表すので、この操作はPush ABC と同じ操作になる。
一方で、Push A(BC)は、Push A ,Push BC と続けて操作することを表す。すなわち、Push A , Push B , Push C と続けて操作することを表すので、この操作はPush ABC と同じ操作になる。
以上より、Push (AB)C = Push ABC = Push A(BC) となる。
命題1、命題2、命題3より次の定理が成立します。
スイッチをいくつか押して、スイッチ達の状態が変化したとき、その変化はスイッチを押す順番によらない。
さらに、同じスイッチは2回以上押してもスイッチ達の状態に新しい変化は起きない。
すなわち、各スイッチは押さないか、一度だけ押すかの二つの操作だけを考えてよい。
この定理から、スイッチの押し方によるスイッチ達の状態の変化の仕方は有限であるといえます。
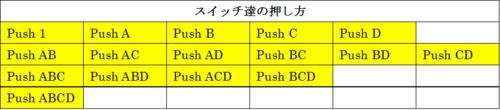
最初の例では、4つのスイッチA,B,C,Dが登場しました。これらの押し方は、まず以下の16通りがあります。
 4-直線スイッチpush表
4-直線スイッチpush表
これら16通り以外の操作をしようとしても、定理4よりスイッチを押す順番を変えて、同じスイッチを2回押す操作を押さない操作に置き換えることを繰り返すと、上の16通りのいずれかになります。
(上の囲いの中には、A,B,C,Dを重複なしで選ぶ場合($ 2^{4} $=16通り)がすべて書き並べている。)
ここで、これまでに登場した0と1で出来た数列の使い方(【on】になっているスイッチを1、【off】になっているスイッチを0としてきた。)を変えてみましょう。
あるスイッチの押し方で、変化するスイッチを1、変化しないスイッチを0として、《全体の変化の仕方》を表してみます。
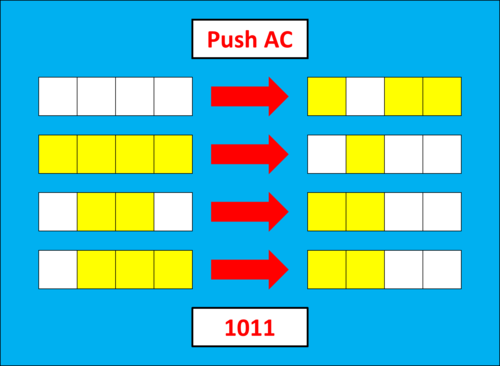
例として Push AC をとると下の図の例より、この操作は4つのスイッチのうちA,C,Dが変化し、Bは変化しない操作だということになります。
A:変化するスイッチ → 1
B:変化しないスイッチ → 0
C:変化するスイッチ → 1
D:変化するスイッチ → 1
これを 1011 と表すことにしましょう。
(この表記の仕方を変化数列と命名しましょう。)
 Push AC変化数列の例
Push AC変化数列の例
これに対して、0と1の初めの定義である、【on】になっているスイッチを1、【off】になっているスイッチを0と置いてできた数列による表記を、変化数列に対応させて表示数列と命名しましょう。
このように、各スイッチの押し方と、それによるスイッチの変化の仕方を数字で表すと、下の表のようになります。
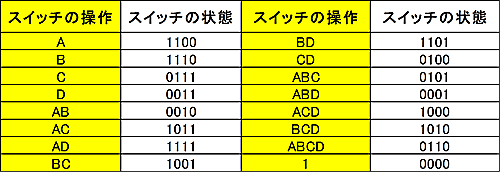 4-直線スイッチの対応表
4-直線スイッチの対応表
この表を見ると、同じ変化の仕方をする異なるPushがないことが分かります。よって、スイッチ達の状態の変化の仕方はPushの場合の数と同じ16通りあることが分かります。
このスイッチ達がとることができる変化の仕方を表す変化数列は、以下の16通りになります。
スイッチ達の変化数列
0000 0001 0010 0100 1000
0011 0101 1001 0110 1010 1100
0111 1011 1101 1110
1111
となり、全部で16通りあります。
(0,1を重複ありで4つ並べる場合の数($ 2^{4} $=16通り)と同じになる。)
ここで注目するポイントは、変化数列の集まりと表示数列の集まりのどちらも、1と0を重複を許して4つ並べたものをすべて含む集合であり、それ以外は含まないものになっていることです。
これより、ある表示数列で表されるスイッチ達に対して、すべてを光らせることができるような変化数列が存在することが言えます。
例えば、表示数列として、1010 で表されるスイッチ達の図にたいして、変化数列として0101 で表される操作を行うと、状態が0であるスイッチB,Dが変化して1になり、1111で表される図に変化します。
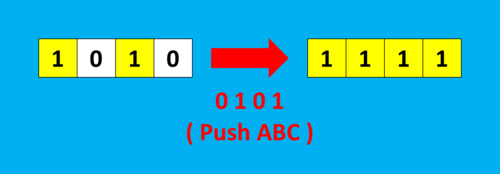 Push ABCの変化数列
Push ABCの変化数列
この例より、ある表示数列で表されるスイッチ達があれば、その数列の1と0をすべて入れ替えた数列を変化数列とする操作をこれに行えば、1111に変化するということが分かります。
上で注目したポイントより、変化数列と表示数列はどちらも16個の数列の集合として表されています。そのため、この集合に含まれるすべての数列には1010 と0101 のような1と0を入れ替えたようなペアが必ず存在します。
したがって、ある表示数列で表されるスイッチ達の図に対して、この数列の1と0を入れ替えた数列で表す変化数列が必ず存在し、この数列に対応する操作を行うと、図は1111 になることが分かります。
これらの話より、スイッチが一直線上に4つ並んだ図の場合、スイッチ達がどのような状態であってもそこからすべてのスイッチ達を光らせることができるような操作が必ず存在することが分かります。
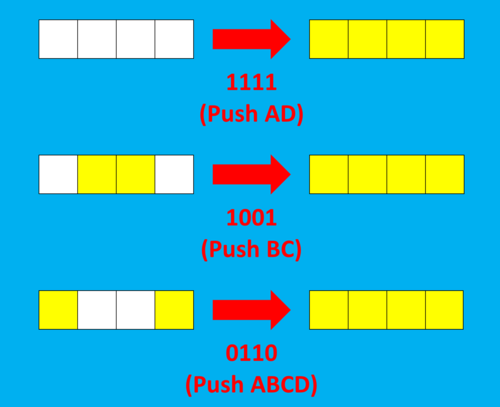 変化数列と表示数列の対応の例
変化数列と表示数列の対応の例
『クロススイッチ問題』 本題
・・・これを見ていると、スイッチが一直線上に4つ並んだ図以外のどんな並び方でも** 表示数列 の数と 操作数列 の数は一致しそうな気がしてきます。
例えば問(1)の並び方でも、表を作ってみるとスイッチ達の変化の仕方に被っているものはありません。(確かめてみて!)つまり、この並び方ではスイッチの状態がどんな場合でも必ずすべてを光らせる操作が存在します。**
それでは、問(2)の並び方の場合だとどうでしょう?対応表を作ってみると、次のようになります。
 1-直線、4-ループ型の図(記号あり)
1-直線、4-ループ型の図(記号あり)
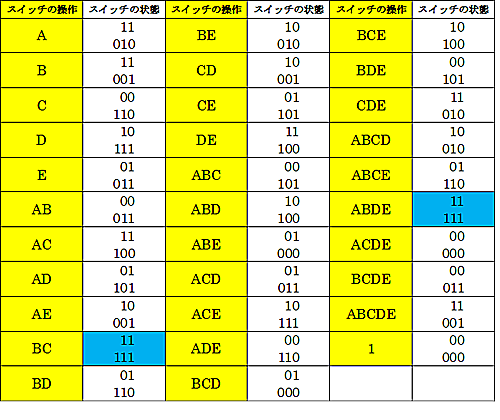 1-直線、4-ループ型の対応表
1-直線、4-ループ型の対応表
・・・見たところ、違う押し方なのに、全く同じ変化になる押し方のペアがいくつかあるようです。
(例えば、Push BC とPush ABDE はともにすべてのスイッチが【on】になる押し方になっている。すなわち、Push BC = Push ABDE )
つまりこの図の場合は、表示数列の数と操作数列の数が違うことになります。これは、はじめのスイッチ達の状態によっては、すべてを光らせることができる操作が存在しないことを表しています。
実際、下の図のような状態の場合は、どうスイッチを押してもすべてを光らせることができません。
 1-直線、4-ループ型スイッチ(無理パターン)
1-直線、4-ループ型スイッチ(無理パターン)
さあ、ここで起こる疑問が今回のメインテーマである、『クロススイッチ問題』です。
まずは用語の定義から参りましょう。
スイッチ達のつながり方が完全であるとは、そのスイッチ達の状態がどのようなものであっても、すべてのスイッチを光らせることができるような操作が存在することである。
また、スイッチ達のつながり方が不完全であるとは、完全でないことである。
つながり方が完全であれば、そのスイッチ図はどのような状態でもパズルに正解が存在することになります。できることなら、図をぱっと見ただけで完全か不完全かが見分けることができればいいなと思うのです。
任意のスイッチ達のつながりに対して、そのつながり方が完全か不完全かを簡単に見分ける方法が存在するか?
実際にすべての操作を試して判断することもできますが、
どのような要素が完全・不完全を分けるのか?
がこの問題のポイントとなります。
まだ予想の範囲内ですが例えば、
- 左右対称なつながり方なら完全なのではないか?
- ループがたくさんあるつながり方は不完全になるのでは?
- 方程式を作れば判断できるのではないか?
- 幾何学の知識がつかえるのでは?
・・・等々あるでしょう。
もしかしたら、すでにこの問題に答えが存在しているにもかかわらず、深く調べもしない自分が勝手に悦に浸っているのかもしれません。
この問題の答えは既にあるぞ!というご意見がありましたら、ぜひお教えください。
知りたいことがもう一つ
さらに、『クロススイッチ問題』に関連してある予想があります。
スイッチ達がすべて【off】の状態から、すべて【on】にできるようなスイッチの押し方が存在したとき、そのスイッチの押し方をFullになる押し方という。
つまり、すべてが1である変化数列が存在することでもある。
任意のスイッチ達のつながり方に対して、Fullになる押し方が存在する。
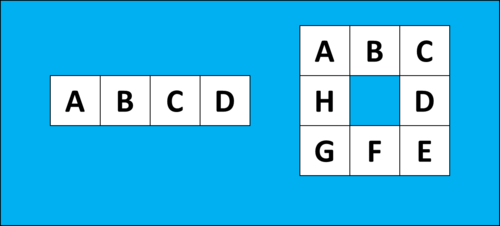 4-直線スイッチ、8-ループスイッチの図(プレーン)
4-直線スイッチ、8-ループスイッチの図(プレーン)
例えば、例として登場した上の二つの図は完全なつながりでした。
スイッチ達がどんな状態でも、すべてを【on】にする押し方があるので、上の定義よりFullになる押し方も存在します。
(一つ目は Push AD 、二つ目は Push ABCDEFGH がFullになる押し方。)
このように完全なつながりに対しては自明なのですが、重要なのは不完全な図にたいしても成り立つのではないかということです。
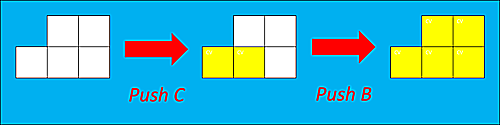 1-直線、4-ループ型の図(Full)
1-直線、4-ループ型の図(Full)
例で確認した、不完全な図である上のスイッチ達でも、
Push BC または Push ABDE
という操作がFullになる押し方になります。
この予想は、
完全なつながり方をするスイッチ達だけでなく、全ての不完全なつながり方をするスイッチ達に対しても、Fullになる押し方が必ず存在するのではないか
ということを言っています。
スイッチ達のすべての変化を確認していけば、答えが分かるのかもしれませんが、スイッチの数がより多く複雑につながっているものになると、単なるごり押しではFullになる押し方を見つけることが難しくなるように思います。
どうにか、この予想を肯定的に示すか、一つ反例を見つけてしまうかしたいのですが、どちらもとても大変そうです。
〆
現在は、クロススイッチ問題と予想の解決方法をやみくもに探しているところです。もし、反例や証明、または既に解決済みだという情報がありましたら、数学見習いの私にご教授願えないでしょうか・・・。
追記:
参考文献があるといいよ、とのことなのでここで提示した予想と全く同じことを考えている日本語の論文がありましたので、ここに追加いたします!