二次関数の係数の符号（2021共通テスト2B第2問前半）

244

はじめに

共通テストの数学2Bで二次関数の接線の問題が出題されたのを受けて，その内容と関連して二次関数の係数の符号についての記事を書く。

グラフの概形与えられたとき，二次関数$y = ax^2 + bx + c$の係数$a$，$b$，$c$の符号を求めよ。

というのはよくある問題である。例えば以下のようなグラフが与えられたとしよう。

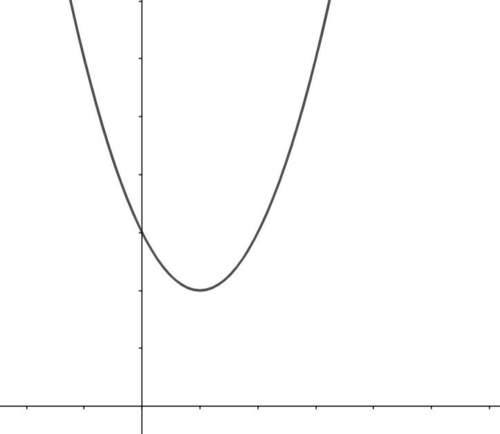二次関数概形

下に凸であるから$a>0$，$y$切片が正であるから$c>0$がすぐにわかる。

では，$b$の符号はどのようにして調べるかをここでは話題にする。

上のような二次関数の概形が与えられたときの1次の係数$b$を一目見ただけで判断せよ。

結論から述べると，先のグラフであれば$b<0$である。

実は以下が成り立っている。

二次関数$y=ax^2 + bx +c$の$x=0$における接線の方程式は$y=bx+c$である。

$y=ax^2 + bx + c$と$y=bx+c$について，辺々引き算すると，$ax^2 = 0$となり，これの解は$x = 0$（重解）である。
したがって，これらの2つのグラフは$x=0$において接している。

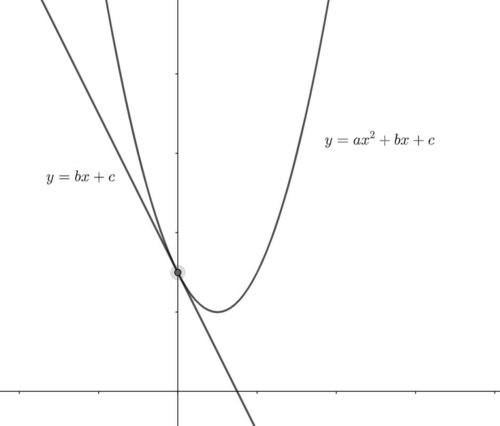二次関数と接線

このことを踏まえると$b<0$であることは明らかである。

また，この事実を用いれば共通テストの2B第2問の前半あたりは即答である。

投稿日：2021年1月18日

高評価したユーザはいません

バッジはありません。

12074

広島県の高校で数学の教員をやっていたはずなのに，気づけば違う仕事をしております。高校数学と大学で学ぶ数学の橋渡しのようなことができればいいなと思っています。記事に誤り等あれば教えてください。

コメントはありません。

読み込み中