自作問題No.1〜解説〜

問題

$a,b,c$は正の実数である。$a+b+c=5,abc=1$のとき$ab+bc+ca$の最小値を求めよ。

まだ解いていない方はこちらから 記事 へ飛べます。答えを見たくない場合はどうぞ。

作問の意図

実は東工大実戦の数学で、これと似た問題を途中で解かなくてはいけない場面に遭遇しまして、恥ずかしながら私は時間内に解けなかったので自戒を込めて作りました。
変数分離するという初歩的な方法を忘れて、三次関数の極値の積でゴリ押ししてしまったんですよね……。
では解説に移りましょう。

解説

$ab+bc+ca=k$とおくと解と係数の関係より、$a,b,c$はそれぞれ三次方程式$x^3-5x^2+kx-1=0$の正の3実数解である。
$k$について解くと$k=-x^2+5x+\displaystyle\frac{1}{x}$(明らかに$x\neq0$なので$x$で両辺割って良い)
ここで右辺を$f(x)$とおき、グラフを描く。
$f'(x)=0$
$-2x+5-\displaystyle\frac{1}{x^2}=0$
$2x^3-5x^2+1=0$
$(2x-1)(x^2-2x-1)=0$
$x=\displaystyle\frac{1}{2},1+\sqrt{2}$($x>0$より)
であるから、以下の画像のように$y=f(x)$と$y=k$の共有点が3実数解(重解含む)を表すような$k$の範囲は$\displaystyle f\left(\frac{1}{2}\right)\leq k \leq f(1+\sqrt{2})$
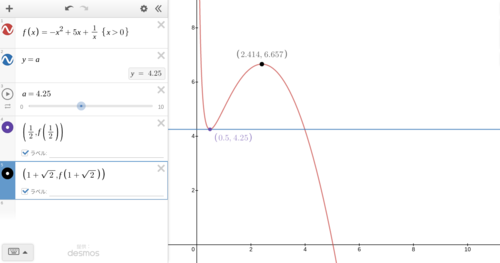描画結果(desmos使用)
よって最小値の候補は$\displaystyle f\left(\frac{1}{2}\right)=\frac{17}{4}$である。実際にこのとき、$a,b,c$のうち2つが$\displaystyle\frac{1}{2}$で重解となっており、もう一つは$4$であるから、最小値は$\displaystyle\frac{17}{4}$として良い。

(別解)
$kx=-x^3+5x^2+1$として三次関数と原点を通る直線の交点の個数問題に帰着させて解くことも可能です。

これ以外に別解などあればぜひコメントください。指摘も歓迎です。