100人の囚人問題: 最善の戦略は？ その2

"100人の囚人問題: 最善の戦略は？ その1" の続きです。この問題・解答がわからない方は、まず"その1"を読むか、他のサイトを参照して頂くのが良いかと思います。

Pointer followingが最善であることの証明

以下、100人の囚人問題で、pointer following("その1"参照)が最善の戦略であり、これより良いものはないことを証明しよう。以下はRef.[1]の解説に書いてあることを、私なりに噛み砕いて説明したものである。

まず、オリジナルの問題を少しだけ変更した以下のゲームAを考える：

このゲームをAとする。このゲームは本質的にオリジナルの問題と同じである（"その1"でもこのゲームに関して成功率を考えた）。

これに対し、以下のゲームBを新たに考える：

これをゲームBとする。最初の人が開けたロッカーに、例えば2→5→3→1が入っていたとしたら、次は4の人の番である。このゲームではひとつもロッカーを開けない人もいる。例えば2→5→3→1の例なら、2の人は最後まで何もしない。

ゲームBには以下3つの重要な性質がある：

1.2.より、ある戦略において、ゲームBの成功率はゲームAの成功率と同じかまたは高いことがわかる。更に3.より、ゲームBの成功率は"定数(=戦略によらない)"なので、その成功率は、ゲームAの成功率の上限を与える（図1参照）。
すなわち、ある戦略でゲームAの成功率がゲームBのそれに等しければ、その戦略がゲームAの最善の戦略（の1つ）である★

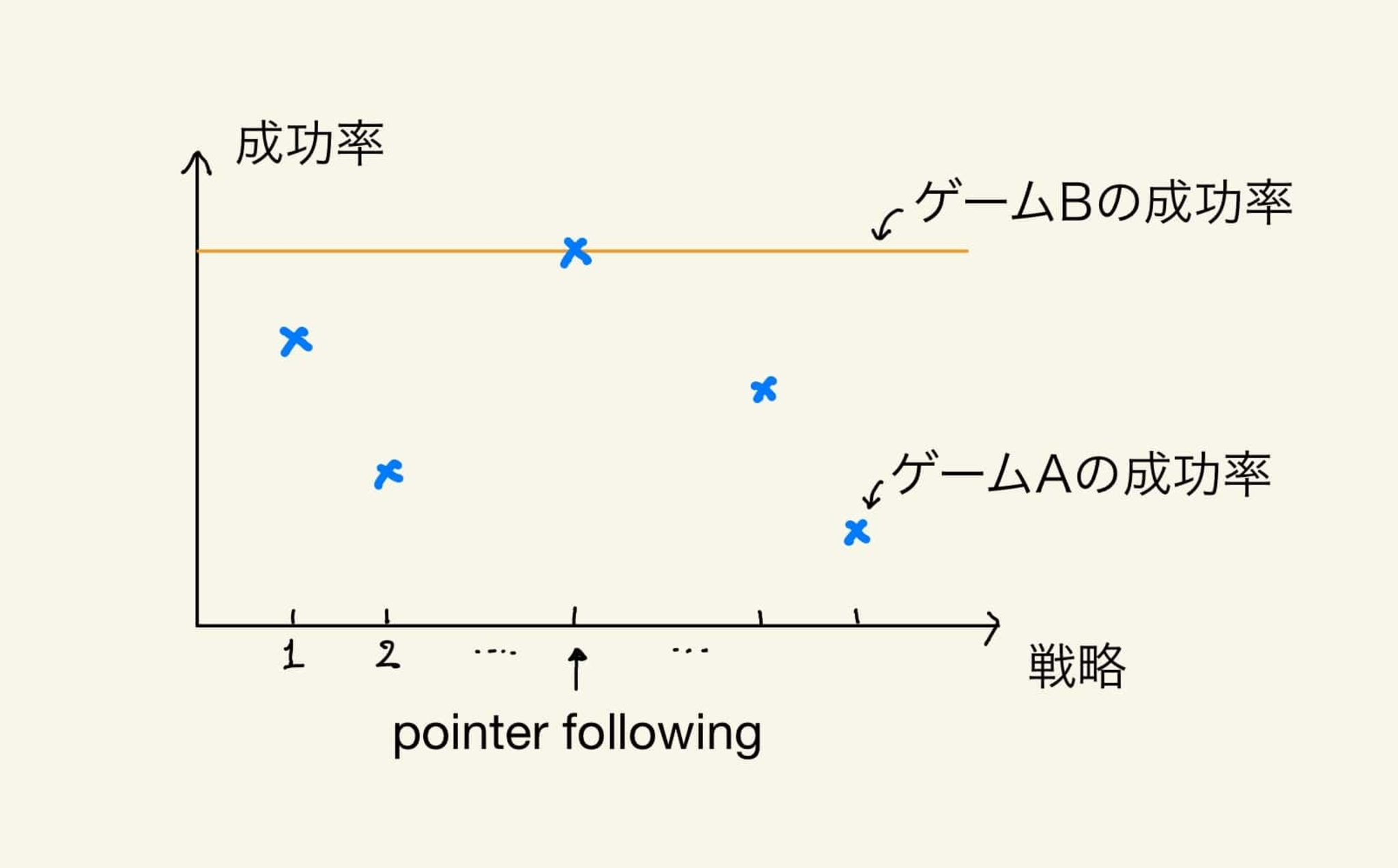ゲームA,Bの成功率とその関係

それぞれの性質の証明は、だいたい以下のような感じであろう：

1.に関しては、ゲームAのメンバーが行うことをBでも行えば良いだけである。ただし、Bでは何もしない人もいる。また、既に開いているロッカーに対しては何もしなければ良い。

2.も簡単である。Aで成功するなら、Aの人たちは皆50個以下のロッカーしか開けてないので、Aと同じロッカーの状態・戦略をとるなら、Bでも同様に50個以下のロッカーしか開けていない。

3.もすぐわかる。Bでは100個のロッカーを開けるが、どのように開けようとも、ランダムにロッカーに名前を入れるなら、戦略に依らず（チートをしなければ）ランダムな名前が出るはずである。

 さて、ではゲームBの成功率と同じゲームAの戦略は何であろうか。お察しのとおり、それはpointer followingである。これは以下のように示すことができる。人とロッカーが$2N$づつ存在する場合を考える。ゲームBで、ロッカーに入っている数字の列を$b_1b_2...b_{2N}$とする。このとき$b_1$から$b_i=1$となる数字までを丸括弧で囲う。次に$b_{i+1}$から$b_j=(b_1$から$b_i$に含まれない最小の数字)までを丸括弧で囲う。これを繰り返し、$b_1b_2...b_{2N}$を$(b_1...b_i)(b_{i+1}...b_j)...(b_{k+1}...b_l)$と表すことができる。すぐにわかるように、それぞれの丸括弧で囲まれた数字が、それぞれの人が開けたときに出てきた数字である。よって、ゲームBで成功するには、この丸括弧の中の数字が$N$個以下であればよい。そしてこの成功条件は、ランダムに$b_1b_2...b_{2N}$というロッカーの状態が与えられたとき、ゲームAにおけるpointer followingでのループが$N$以下である条件と等しい（ループの概念は"その1"や他の文献を参照してください）。つまり、ゲームAでpointer followingを採用すれば、その成功率はゲームBでの成功率と等しい。よって★より、pointer followingが100人の囚人問題に対する最善の戦略であることが示された。

 ここで2.に関してコメントしておく。次のことに注意されたい：ある状態のロッカーに対し、ある戦略でゲームAで失敗したとしても、その戦略でゲームBで失敗するとは限らない。実際、ある状態のロッカー・ある戦略でゲームAで失敗し、かつゲームBで成功する例を作ることは難しくはない。もし「ゲームAで失敗$\rightarrow$Bでも失敗」とすると、ゲームBの成功率はゲームAのそれの下限を与えることになってしまう。ゲームAとゲームBにおいて成功・失敗が等価になり、そうなるとゲームAの成功・失敗も戦略によらないというおかしなことになってしまう。

最後に

この証明で重要なのは

である。

この上限は、100人の名前がどれも一様に現れる場合の話である。もしこれが成り立たなければ、もっと成功率が高い戦略は存在する。例えば、開けたロッカーの中に入っている名前を入れ替えても良いとすると、これを名前の順に並び替えることで、二分法を使った探索により46%程度の成功率を達成することができる。この時、名前の出現率の一様性は成立していない。

以上で最善の戦略に関するコメントを終わりにする。Ref.[1]にはこの問題の歴史やopen problemも書いてあるので、興味がある方は読まれると良いかと思う。