3
解説競技数学
学校の図書館のどこかの本に載ってた問題
88
3
$$$$
どっかの本に載ってて面白いなと思った問題( こちら )の解説です
下の図のxの長さを求めよ。
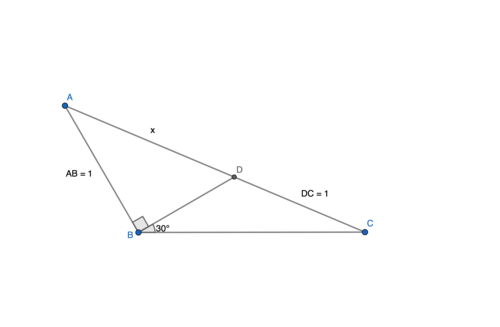図1
解説
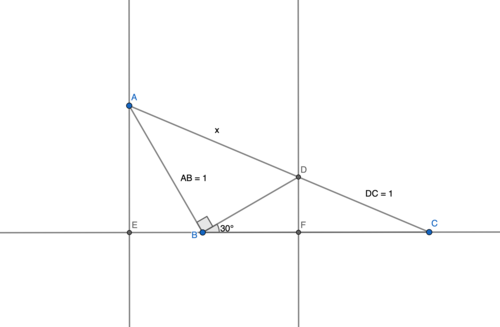図2
図のようにA,DからそれぞれBCに下ろした垂線の足をE,Fとする。
このとき、$\angle{ABE} = 60^\circ$よりAE=$\frac{\sqrt{3}}{2}$
また、$\triangle{ABD}$で三平方の定理より$BD = \sqrt{x^2 - 1}$
$\angle{DBF} = 30^\circ$より$DF = \frac{\sqrt{x^2 - 1}}{2}$
ここで$AE/\!/DF$より、$AE:DF = AC:DC$
よって
$\frac{\sqrt{3}}{2}:\frac{\sqrt{x^2-1}}{2} = x + 1:1$
$\therefore\frac{\sqrt{3}}{2}\cdot 1 = (x + 1)\cdot\frac{\sqrt{x^2 - 1}}{2}$
$\therefore\sqrt{3}=(x + 1)\sqrt{x^2 - 1}$
両辺0以上より両辺二乗して
$3 = (x + 1)^2(x^2 - 1)$
これを整理して $x^4+2x^3 - 2x - 4=0$
これにx=-2を代入すると0になることがわかるので,左辺は(x+2)を因数にもつから因数分解して
$(x+2)(x^3-2) = 0$
xは正の実数より$x=\sqrt[3]{2}$
.
なんと２の３乗根になります。面白いですねえ
ちなみにこの図は目盛りなし定規とコンパスだけでは作図不可能ですが、目盛りあり定規なら作図できますね。
投稿日：2021年2月7日
更新日：2021年11月7日
投稿者
投稿者
この記事を高評価した人
この記事を高評価した人
高評価したユーザはいません
コメント
コメント