正n角形を円と放物線の交点で表現する

317

はじめに

　この記事ではポテト一郎さんのツイートを発端として最近話題(?)になっている正 $n$ 角形の円と放物線による表現について私なりに考察した結果を紹介します。
　その話題となっている一連のツイートがこちらになります。

【吃驚仰天！正七角形！？】
なな、なんと、円と２本の放物線の交点を結んで正七角形をつくることができるそうです。先ほど初めて知り私もやってみました。そして、その美しさに感動しました。松田康雄先生が発見し、2019年に算額が高見神社に奉納されたとのことです。いつか実物を見に行きたいです！ pic.twitter.com/VptFWHlpRl
— ポテト一郎🥔 (@potetoichiro) February 14, 2021

【拡張！正十三角形！？】
円と４本の放物線の交点を結んで正十三角形をつくることに成功しました。我ながら頑張りました！ https://t.co/mjKpObvbWK pic.twitter.com/aNCX1kXqXo
— ポテト一郎🥔 (@potetoichiro) February 15, 2021

Enneadecagon. Equations later ... pic.twitter.com/KP4UbWeGLm
— Ignacio Larrosa Cañestro (@ilarrosac) February 15, 2021

It seems that most of the parabolas that go through 3 of the vertices, go through a fourth. In the case of the icosapenthagon, I had a hard time choosing them to cover the other 24 vertices. Finding exact expressions with radicals for their coefficients is more complicated ... pic.twitter.com/hsVMip19i4
— Ignacio Larrosa Cañestro (@ilarrosac) February 16, 2021

　この4つのツイートでは正 $7, 13, 19, 25$ 角形(の頂点)が円と放物線の交点として表現されています。このことについて私なりに考察して、その結果を利用したところひとまず正 $31, 37$ 角形でも同じことができることを確認できました。

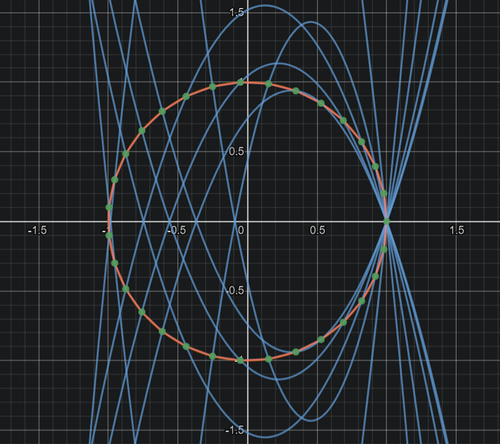正31角形

正三十一角形 pic.twitter.com/oU6GHrXOkn
— しょう (@emiemi_ogaoga) February 17, 2021

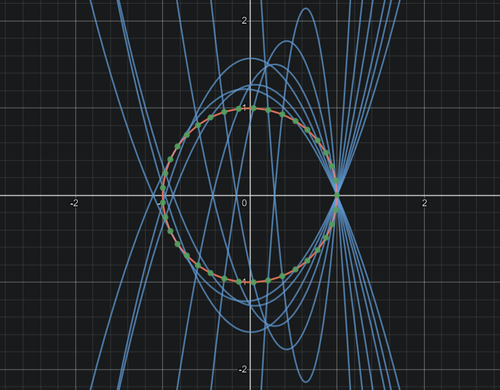正37角形

正三十七角形できちゃった pic.twitter.com/8tAO5wb8ms
— しょう (@emiemi_ogaoga) February 17, 2021

　以下で私がどうやってこの結果を得たのかを紹介していきます。

考察

問題の内容

　まずこれらの表現が満たすべき条件というのを定めましょう。

正 $n$ 角形の各頂点が円 $x^{2} + y^{2} = 1$ と放物線の交点となっている。
すべての放物線は合計 $4$ つの頂点を表すものとする。
すべての放物線は点 $(1, 0)$ を通り、その他の頂点で交わることはないものとする。

　このような表現ができる $n$ についての条件、またはこのような表現ができるときどのように放物線を取ればよいのかを考えるのが今回の問題となります。
　とりあえずこの条件から $n$ は $3 k + 1$ ( $k$ は正整数)の形で表される場合に限って問題が考えられることがわかります。 $x$ 軸対称であったほうが扱いやすいので以下 $n$ は $6 k + 1$ 型の自然数ということにしましょう。

放物線と円の交点

　まず放物線が表す $4$ つの頂点についての条件を考えます。そこで上で紹介した $4$ つのツイートをよく見てみると以下の法則が成り立つことがわかりました。

　 $3$ 点 $(1, 0), (\cos a, \sin a), (\cos b, \sin b)$ を通る放物線は点 $(\cos (a + b), - \sin (a + b))$ も通る。

　仮定を満たすような放物線の方程式はラグランジュの補間公式より
$y = \frac{(x - 1) (x - \cos b)}{(\cos a - 1) (\cos a - \cos b)} \sin a + \frac{(x - 1) (x - \cos a)}{(\cos b - 1) (\cos b - \cos a)} \sin b$
と表せる。
　この右辺に $x = \cos (a + b)$ を代入すると
$\begin{array}{rcl} \frac{\cos (a + b) - 1}{\cos a - \cos b} (\frac{\cos (a + b) - \cos b}{\cos a - 1} \sin a - \frac{\cos (a + b) - \cos a)}{\cos b - 1} \sin b) \\ = & \frac{- 2 \sin^{2} (\frac{a + b}{2})}{- 2 \sin (\frac{a + b}{2}) \sin (\frac{a - b}{2})} (\frac{- 2 \sin (\frac{a + 2 b}{2}) \sin (\frac{a}{2})}{- 2 \sin^{2} (\frac{a}{2})} \cdot 2 \sin (\frac{a}{2}) \cos (\frac{a}{2}) - \frac{- 2 \sin (\frac{2 a + b}{2}) \sin (\frac{b}{2})}{- 2 \sin^{2} (\frac{b}{2})} \cdot 2 \sin (\frac{b}{2}) \cos (\frac{b}{2})) \\ = & \frac{\sin (\frac{a + b}{2})}{\sin (\frac{a - b}{2})} (2 \sin (\frac{a + 2 b}{2}) \cos (\frac{a}{2}) - 2 \sin (\frac{2 a + b}{2}) \cos (\frac{b}{2})) \\ = & \frac{\sin (\frac{a + b}{2})}{\sin (\frac{a - b}{2})} ((\sin (a + b) + \sin b) - (\sin (a + b) + \sin a)) \\ = & \frac{\sin (\frac{a + b}{2})}{\sin (\frac{a - b}{2})} \cdot (- 2 \sin (\frac{a - b}{2}) \cos (\frac{a + b}{2})) \\ = & - 2 \sin (\frac{a + b}{2}) \cos (\frac{a + b}{2}) \\ = & - \sin (a + b) \end{array}$
を得る。

すなわち頂点
$(\cos \frac{2 π i}{n}, \sin \frac{2 π i}{n}), (\cos \frac{2 π j}{n}, \sin \frac{2 π j}{n})$
を表す放物線が表すもう一つの頂点は
$(\cos (- \frac{2 π (i + j)}{n}), \sin (- \frac{2 π (i + j)}{n}))$
となるということです。

追記

　もう少しスマートな証明法がないか模索してみたところ次の主張を示すことができました。

　複素数平面において円 $| z | = 1$ と放物線が異なる $4$ 点 $z_{1}, z_{2}, z_{3}, z_{4}$ で交わるとき $z_{1} z_{2} z_{3} z_{4} = 1$ が成り立つ。

　放物線は焦点 $α$ からの距離と準線 $Im (z) = b$ からの距離が等しい点の集合であるのでその方程式は
$| z - α | = | b - Im (z) |$
となる。これと円 $| z | = 1$ の交点を考えると $z \overset{―}{z} = 1$ から
$\begin{aligned} z^{2} | z - α |^{2} & = z (z - α) (\overset{―}{z} z - \overset{―}{a} z) = z (z - α) (1 - \overset{―}{α} z) \\ 4 z^{2} | b - Im (z) |^{2} & = {(2 b z - \frac{z^{2} - z \overset{―}{z}}{i})}^{2} = - (2 b i z - z^{2} + 1)^{2} \end{aligned}$
なので $z$ についての四次方程式
$\begin{aligned} 4 z^{2} | z - α |^{2} - 4 z^{2} | b - Im (z) |^{2} \\ = & 4 z (z - α) (1 - \overset{―}{a} z) + (2 b i z - z^{2} + 1)^{2} = 0 \end{aligned}$
と $| z | = 1$ の共通解を求めればよい。
　特に上の四次方程式の定数項は $1$ であるのでその解を $z = z_{1}, z_{2}, z_{3}, z_{4}$ とおくと解と係数の関係から
$z_{1} z_{2} z_{3} z_{4} = 1$
が成り立つ。

表現の構造

　では上で紹介した $4$ つのツイートにおいて $(i, j)$ の組はどのように取られていたのか見てみましょう。
　正 $6 k + 1$ 角形に対する表現は $x$ 軸対称で計 $2 k$ 本の放物線からなるので $k$ 本の放物線について以下に記します( $- (i + j)^{'}$ の項は $- (i + j)$ を $(i + j)$ ( $x$ 軸反転)または $n - (i + j)$ (偏角の周期性)で置き換えて $3 k = \frac{n - 1}{2}$ 未満にしたものとしました)、

$n = 7 (k = 1)$ のとき
$\begin{array}{cccc} i & j & - (i + j) & - (i + j)^{'} \\ 1 & 2 & - 3 & 3 \end{array}$
$n = 13 (k = 2)$ のとき
$\begin{array}{cccc} i & j & - (i + j) & - (i + j)^{'} \\ 1 & 3 & - 4 & 4 \\ 2 & 5 & - 7 & 6 \end{array}$
$n = 19 (k = 3)$ のとき
$\begin{array}{cccc} i & j & - (i + j) & - (i + j)^{'} \\ 1 & 4 & - 5 & 5 \\ 2 & 6 & - 8 & 8 \\ 3 & 7 & - 10 & 9 \end{array}$
$n = 25 (k = 4)$ のとき
$\begin{array}{cccc} i & j & - (i + j) & - (i + j)^{'} \\ 1 & 11 & - 12 & 12 \\ 2 & 6 & - 8 & 8 \\ 3 & 7 & - 10 & 10 \\ 4 & 5 & - 9 & 9 \end{array}$

　これを見てわかる通りこの表の $i, j, - (i + j)^{'}$ の列で $1$ から $3 k = \frac{n - 1}{2}$ までの番号が尽くされることになります。
　逆に $i, j, - (i + j)^{'}$ の列で $1$ から $3 k$ までの番号が尽くされるように $(i, j)$ が取れることが表現の存在する必要十分条件となることは簡単にわかります。

表現の構成

　上の理屈で組 $(i, j)$ を構成していくとより $5 \leq k$ における表現も得られそうです。
　というわけで $k = 5, 6$ のときについてまず $i = 1, 2, \dots, k$ と並べて $j$ にテキトーに数字を当てはめてみると

$n = 31 (k = 5)$ のとき
$\begin{array}{cccc} i & j & - (i + j) & - (i + j)^{'} \\ 1 & 14 & - 15 & 15 \\ 2 & 7 & - 9 & 9 \\ 3 & 10 & - 13 & 13 \\ 4 & 8 & - 12 & 12 \\ 5 & 6 & - 11 & 11 \end{array}$
$n = 37 (k = 6)$ のとき
$\begin{array}{cccc} i & j & - (i + j) & - (i + j)^{'} \\ 1 & 7 & - 8 & 8 \\ 2 & 9 & - 11 & 11 \\ 3 & 10 & - 13 & 13 \\ 4 & 14 & - 18 & 18 \\ 5 & 12 & - 17 & 17 \\ 6 & 15 & - 21 & 16 \end{array}$

　という表が(偶然)できたので冒頭で私が示したような表現が得られたのでした。
　 $k = 1, 2, 3, 4, 5, 6$ において $i = 1$ に対する $j$ の値が $k + 1$ または $3 k - 1$ とできるのは少し興味深いですね。

追記

表現の個数について

　上では $k = 1, 2, 3, 4, 5, 6$ に対して少なくとも一つは表現が存在していることを示しましたがその表現は果たして一意的なのでしょうか？
　答えはNoです。
　簡単なプログラムを書いて虱潰し的に $(i, j)$ の取れ方を探索してみた(ただし $i$ の値は $i = 1, 2, \dots, k$ と固定した)ところ $k = 1, 2$ のときは確かに一意的でしたが $k = 3$ のときは

$n = 19 (k = 3)$ のとき
$\begin{array}{cccc} i & j & - (i + j) & - (i + j)^{'} \\ 1 & 4 & - 5 & 5 \\ 2 & 6 & - 8 & 8 \\ 3 & 7 & - 10 & 9 \end{array} \begin{array}{cccc} i & j & - (i + j) & - (i + j)^{'} \\ 1 & 5 & - 6 & 6 \\ 2 & 8 & - 10 & 9 \\ 3 & 4 & - 7 & 7 \end{array}$

と $2$ 通りの表現が、 $k = 4$ のときは

$n = 25 (k = 4)$ のとき
$\begin{array}{cccc} i & j & - (i + j)^{'} \\ 1 & 11 & 12 \\ 2 & 6 & 8 \\ 3 & 7 & 10 \\ 4 & 5 & 9 \end{array} \begin{array}{cccc} i & j & - (i + j)^{'} \\ 1 & 11 & 12 \\ 2 & 7 & 9 \\ 3 & 5 & 8 \\ 4 & 6 & 10 \end{array} \begin{array}{cccc} i & j & - (i + j)^{'} \\ 1 & 10 & 11 \\ 2 & 5 & 7 \\ 3 & 6 & 9 \\ 4 & 8 & 12 \end{array} \begin{array}{cccc} i & j & - (i + j)^{'} \\ 1 & 6 & 7 \\ 2 & 10 & 12 \\ 3 & 8 & 11 \\ 4 & 5 & 9 \end{array} \begin{array}{cccc} i & j & - (i + j)^{'} \\ 1 & 5 & 6 \\ 2 & 8 & 10 \\ 3 & 9 & 12 \\ 4 & 7 & 11 \end{array} \begin{array}{ccc} i & j & - (i + j)^{'} \\ 1 & 5 & 6 \\ 2 & 9 & 11 \\ 3 & 7 & 10 \\ 4 & 8 & 12 \end{array}$

と $6$ 通りの表現が、 $k = 5$ のときは

$n = 31 (k = 5)$ のとき
$\begin{array}{ccc} i & j & - (i + j) \\ 1 & 14 & 15 \\ 2 & 7 & 9 \\ 3 & 10 & 13 \\ 4 & 8 & 12 \\ 5 & 6 & 11 \end{array} \begin{array}{ccc} i & j & - (i + j) \\ 1 & 14 & 15 \\ 2 & 10 & 12 \\ 3 & 6 & 9 \\ 4 & 7 & 11 \\ 5 & 8 & 13 \end{array} \begin{array}{ccc} i & j & - (i + j) \\ 1 & 13 & 14 \\ 2 & 8 & 10 \\ 3 & 6 & 9 \\ 4 & 11 & 15 \\ 5 & 7 & 12 \end{array} \begin{array}{ccc} i & j & - (i + j) \\ 1 & 13 & 14 \\ 2 & 6 & 8 \\ 3 & 9 & 12 \\ 4 & 7 & 11 \\ 5 & 10 & 15 \end{array} \begin{array}{ccc} i & j & - (i + j) \\ 1 & 12 & 13 \\ 2 & 6 & 8 \\ 3 & 7 & 10 \\ 4 & 11 & 15 \\ 5 & 9 & 14 \end{array} \begin{array}{ccc} i & j & - (i + j) \\ 1 & 9 & 10 \\ 2 & 6 & 8 \\ 3 & 13 & 15 \\ 4 & 7 & 11 \\ 5 & 12 & 14 \end{array} \begin{array}{ccc} i & j & - (i + j) \\ 1 & 8 & 9 \\ 2 & 13 & 15 \\ 3 & 11 & 14 \\ 4 & 6 & 10 \\ 5 & 7 & 12 \end{array} \begin{array}{ccc} i & j & - (i + j) \\ 1 & 7 & 8 \\ 2 & 13 & 15 \\ 3 & 9 & 12 \\ 4 & 10 & 14 \\ 5 & 6 & 11 \end{array} \begin{array}{ccc} i & j & - (i + j) \\ 1 & 7 & 8 \\ 2 & 11 & 13 \\ 3 & 12 & 15 \\ 4 & 6 & 10 \\ 5 & 9 & 14 \end{array} \begin{array}{ccc} i & j & - (i + j) \\ 1 & 7 & 8 \\ 2 & 9 & 11 \\ 3 & 13 & 15 \\ 4 & 6 & 10 \\ 5 & 12 & 14 \end{array} \begin{array}{ccc} i & j & - (i + j) \\ 1 & 7 & 8 \\ 2 & 10 & 12 \\ 3 & 6 & 9 \\ 4 & 13 & 14 \\ 5 & 11 & 15 \end{array} \begin{array}{ccc} i & j & - (i + j) \\ 1 & 6 & 7 \\ 2 & 9 & 11 \\ 3 & 12 & 15 \\ 4 & 10 & 14 \\ 5 & 8 & 13 \end{array} \begin{array}{ccc} i & j & - (i + j) \\ 1 & 6 & 7 \\ 2 & 12 & 14 \\ 3 & 8 & 11 \\ 4 & 9 & 13 \\ 5 & 10 & 15 \end{array} \begin{array}{ccc} i & j & - (i + j) \\ 1 & 6 & 7 \\ 2 & 8 & 10 \\ 3 & 9 & 12 \\ 4 & 13 & 14 \\ 5 & 11 & 15 \end{array}$

と $14$ 通りの表現が存在し、長くなるので詳細は省きますが $k = 6$ のときは $62$ 通り、 $k = 7$ のときは $262$ 通り、 $k = 8$ のときは $1264$ 通りほどあるようです。こうして指数関数やら階乗やらの速さで増えていく様子を見ると正 $6 k + 1$ 角形については必ず表現が存在しそうな感じがしますね。

$6 k + 1$ が素数のとき

　先ほど yotsunva さんの以下のツイートに連なる議論を見かけまして、どうやら $n = 6 k + 1$ が素数であるときは表現の存在が保証されるとともに"ある条件"を満たすようなものがただ一つ定まるようです。

放物線と円の交点4つの内3つがその正多角形の頂点のいずれかと一致するときに4点目も頂点のいずれかと一致することは偶然ではないし、放物線をより高次な曲線にしても同様のことが言える（4点目がどこかということも含めて Abel's theorem からわかる） https://t.co/fpKRu1EOUU
— yotsunva (@yotsunva) February 15, 2021

　 $n = 6 k + 1$ が素数のときは正 $n$ 角形に対する表現が存在する。
　特に任意の放物線についてそれが表す四頂点を
$(1, 0), (\cos \frac{2 π a}{n}, \sin \frac{2 π a}{n}), (\cos \frac{2 π b}{n}, \sin \frac{2 π b}{n}), (\cos \frac{2 π c}{n}, \sin \frac{2 π c}{n})$
とおくと
$a^{3} \equiv b^{3} \equiv c^{3} (\mod n)$
を満たすようなものがただ一つ存在する。

　いま上での議論から正 $n$ 角形を円と放物線の交点で表現する問題は $Z / n Z$ の $0$ 以外の元( $n$ は素数でとしていたのでつまり $(Z / n Z)^{\times}$ の元)を $2 k$ 個の三つ組
${a, b, c} (a + b + c \equiv 0 (\mod n))$
に分ける問題に帰結されるのであった。
　特にこれらの三つ組が全て
$a^{3} \equiv b^{3} \equiv c^{3} (\mod n)$
を満たすように取れるためには準同型
$f : (Z / n Z)^{\times} \to (Z / n Z)^{\times} x \mapsto x^{3}$
について $| Ker f | = 3$ が成り立ち、また任意の剰余類
$A = {a, b, c} \in (Z / n Z)^{\times} / Ker f$
が $a + b + c = 0$ を満たすことを示せばよい。
　ここで素数 $n$ の原始根の一つを $r$ とおくと $(Z / n Z)^{\times}$ の任意の元 $x$ は
$x = r^{j} (0 \leq j < n - 1)$
の形に一意に表せ、このとき $r$ の位数は $n - 1 = 6 k$ であることに注意すると
$f (x) = r^{3 j} = 1 ⟺ 3 j | 6 k ⟺ j = 0, 2 k, 4 k$
つまり $| Ker f | = 3$ を得る。
　またこのことから任意の剰余類 $A \in (Z / n Z)^{\times} / Ker f$ は
$A = r^{j} Ker f = {r^{j}, r^{j + 2 k}, r^{j + 4 k}} (0 \leq j < 2 k)$
の形に一意に表せ、このとき
$r^{j} + r^{j + 2 k} + r^{j + 4 k} = r^{j} \frac{r^{6 k} - 1}{r^{2 k} - 1} \equiv 0 (\mod n)$
が成り立つことから主張を得る。

議論の帰結

　中国剰余定理から議論を帰結できないか考えてみたところ $n$ の異なる素因数の個数が $1$ 個か $2$ 個の場合に帰結できることがわかりました。

　 $n$ を互いに素な真の約数の積
$n = M N (M, N > 1, gcd (M, N) = 1, M, N \equiv 1 (\mod 6))$
に分解したとき、正 $M, N$ 角形に対する表現が存在すれば正 $n$ 角形に対する表現が存在する。

　 $M = 6 i + 1, N = 6 j + 1$ とおくと
$n = M N = (6 j + 1) (6 i + 1) = 6 k + 1$
より $k = 6 i j + i + j$ が成り立つことに注意する。
　いま仮定より $Z / M Z, Z / N Z$ (から $0$ を除いたもの)はそれぞれ $2 i, 2 j$ 個の $3$ つ組
${a, b, c} (a + b + c \equiv 0 (\mod M, N))$
に分割できる。そのような分割をそれぞれ
$A_{s}, B_{t} (1 \leq s \leq 2 i, 1 \leq t \leq 2 j)$
とおく。
　このとき中国剰余定理から環同型写像
$φ : (Z / M Z) \times (Z / N Z) \to Z / n Z$
を取り、 $M, N$ に関する $3$ つ組
$A_{s} = {a, b, c}, B_{t} = {d, e, f}$
に対し $Z / n Z$ の元の組
${φ (a, d), φ (b, e), φ (c, f)}$
を考えるとその和は
$φ (a + b + c, d + e + f) = φ (0, 0) \equiv 0 (\mod n)$
を満たすのでこれは $n$ に関する $3$ つ組となる。
　さて各 $s, t$ について $A_{s} = {a, b, c}$ と $B_{t} = {d, e, f}$ によって構成できる $n$ の $3$ つ組は全部で $6$ 通りあるが、同じ要素を持つ $3$ つ組
${φ (a, d), φ (b, e), φ (c, f)}, {φ (a, d), φ (b, f), φ (c, e)}$
は共存できないことに注意すると計 $3$ つの分割が作れる。また
${φ (a, 0), φ (b, 0), φ (c, 0)}, {φ (0, d), φ (0, e), φ (0, f)}$
も $n$ の $3$ つ組になるので以上のようにして $12 i j + 2 i + 2 j = 2 k$ 個の $3$ つ組への分割を構成することができ、主張を得る。

　 $n$ が素数冪
$n = p^{e} (p \equiv 1 (\mod 6))$
の形に表せるとき、正 $n$ 角形に対する表現が存在する。

　良く知られているように $p \geq 3$ に対して $(Z / p^{e} Z)^{\times}$ は巡回群となるのでその生成元の一つを $r$ とおくと $Z / p^{e} Z$ は
$\sum_{i = 0}^{e - 1} p^{e - i - 1} \frac{p - 1}{3} = \frac{p^{e} - 1}{3} = 2 k$
個の $3$ つ組
${p^{i} r^{j}, p^{i} r^{j + p^{e - i - 1} \frac{p - 1}{3}}, p^{i} r^{j + p^{e - i - 1} \frac{2 (p - 1)}{3}}} (0 \leq i < e, 0 \leq j < p^{e - i - 1} \frac{p - 1}{3})$
に分割できるので主張を得る( $r$ は $(Z / p^{e^{'}} Z)^{\times} (e^{'} \leq e)$ の生成元でもあることに注意する)。

　任意の正 $n$ 角形 $(n \equiv 1 (\mod 6))$ に対して表現が存在することを示すには
$p, q (p \neq q, p, q \equiv - 1 (\mod 6))$
を素数として $n = p^{e} (2 ∣ e)$ または $n = p^{e} q^{f} (2 ∤ e, 2 ∤ f)$ の場合について示せば十分である。

　補題4から $n$ をどのように互いに素な真の約数 $M, N$ の積に分解しても $M, N \equiv - 1 (\mod 6)$ が成り立つ場合を考えればよい。
　このとき $n$ が $3$ つ以上の異なる素因数を持つとすると、その中から任意に $3$ つの素因数 $p, q, r$ を選び $n = p^{e} q^{f} r^{g} n^{'} (p, q, r ∤ n^{'})$
とおくと仮定より
$p^{e}, q^{f}, r^{g} \equiv - 1 (\mod 6)$
でなければならないが $n$ の真の約数 $N = p^{e} q^{f}$ は $N \equiv 1 (\mod 6)$ を満たすので矛盾。
　また $n$ が丁度 $2$ つの異なる素因数を持つとき $n = p^{e} q^{f}$ とおくと
$p^{e}, q^{f} \equiv - 1 (\mod 6)$
であるためには $p, q \equiv - 1 (\mod 6)$ かつ $2 ∤ e, 2 ∤ f$ であればよく、
　 $n$ が素数冪 $p^{e}$ であるときは定理 $5$ から $p \equiv - 1 (\mod 6)$ の場合について考えればよく、 $p^{e} = n \equiv 1 (\mod 6)$
であるためには $2 ∣ e$ であればよい。

まとめ

　 $2 k$ 個の $3$ つ組
${a, b, c} (a + b + c \equiv 1 (\mod n))$
への分割が存在するか否かや、 $3$ つ組 $(a, b, c)$ を構成するアルゴリズムは $n$ が素数のときを除いて未だ不明ですが $(i, j)$ の組を構成したときと同様の手法でより高次の正 $n$ 角形についての表現を得ることができるんじゃないかなと思います。
　良ければ皆さんも正 $n$ 角形の表現を探してみてはいかがでしょうか。では。

投稿日：2021年2月17日

更新日：2024年5月12日

この記事を高評価した人

高評価したユーザはいません

この記事に送られたバッジ

バッジはありません。

バッチを贈って投稿者を応援しよう

バッチを贈ると投稿者に現金やAmazonのギフトカードが還元されます。

投稿者

子葉

1105

274415

主に複素解析、代数学、数論を学んでおります。私の経験上、その証明が簡単に探しても見つからない、英語の文献を漁らないと載ってない、なんて定理の解説を主にやっていきます。同じ経験をしている人の助けになれば。最近は自分用のノートになっている節があります。

他の人のコメント

コメントはありません。

読み込み中

子葉

正n角形を円と放物線の交点で表現する

はじめに
考察
問題の内容
放物線と円の交点
表現の構造
表現の構成
追記
表現の個数について
$6 k + 1$ が素数のとき
議論の帰結
まとめ

正n角形を円と放物線の交点で表現する

はじめに

考察

問題の内容

放物線と円の交点

追記

表現の構造

表現の構成

追記

表現の個数について

6k+1が素数のとき

議論の帰結

まとめ

この記事を高評価した人

この記事に送られたバッジ

投稿者

コメント

他の人のコメント

$6 k + 1$ が素数のとき