お子様には見せちゃダメ!? オトナのヒミツの結合則♡

お子様には見せちゃイケナイ計算

本計算は、取り扱いに十分な注意が必要です。用法をよく守り、
分配則を習いたてのお子様の手の届かないところに保管してください。

$$\quad\begin{array}{l&c&l&r} a\times(b+c)&=&a+(b\times c)\\[8pt] 1×(1+1)&=&1+(1×1)&=&2\\ 2×(3+4)&=&2+(3×4)&=&14\\ 3×(4+9)&=&3+(4×9)&=&39\\ 3×(5+6)&=&3+(5×6)&=&33\\ 4×(5+16)&=&4+(5×16)&=&84\\ 4×(7+8)&=&4+(7×8)&=&60\\ 5×(6+25)&=&5+(6×25)&=&155\\ 5×(7+15)&=&5+(7×15)&=&110\\ 5×(9+10)&=&5+(9×10)&=&95\\ 6×(7+36)&=&6+(7×36)&=&258\\ 6×(11+12)&=&6+(11×12)&=&138\\ 7×(8+49)&=&7+(8×49)&=&399\\ 7×(9+28)&=&7+(9×28)&=&259\\ 7×(10+21)&=&7+(10×21)&=&217\\ 7×(13+14)&=&7+(13×14)&=&189\\ 8×(9+64)&=&8+(9×64)&=&584\\ 8×(15+16)&=&8+(15×16)&=&248\\ &&\vdots&& \end{array}$$

ヒミツのしくみと用法

下の図は、二通りの方法でチョコレートの面積を出しています。

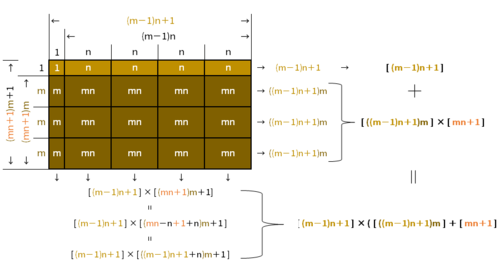
つまり、

$$\quad\begin{align} &[ (m-1)n+1 ] + \left([ mn+1 ] \times [ ((m-1)n+1)m ]\right)\\[8pt] =&[ (m-1)n+1 ] \times \left([ mn+1 ] + [ ((m-1)n+1)m ]\right)\\ \end{align} $$

ということですね。

$m$ と $n$ にお好きな数を入れてお楽しみください。

積の和は。

$\cdots$以上、ヒミツの交換則でした。