合成関数の微分の式のイラスト

合成関数の微分のイメージ図

集合A,Bは$\mathbb{R}$の開集合で$f:A\rightarrow\mathbb{R}$,$g:B\rightarrow\mathbb{R}$;$f(A)\subseteq B$とし、$f,g$は可微分函数とする。さらに、$f$は任意の$x\in A$に対して、$\forall \epsilon>0,\exists a,\exists b \in B_{\epsilon}(x),f(a)=f(b)$を満たさないものとする。(そこのエリアだけ平らな「台地」や「盆地」があったり「凄く振動する場所」があったりはしないものとする。※$B_{\epsilon}(x)$は$x$の$\epsilon$近傍)
　この時、$f,g$の合成関数$g\circ f$の微分の式のイメージは以下のような感じ。

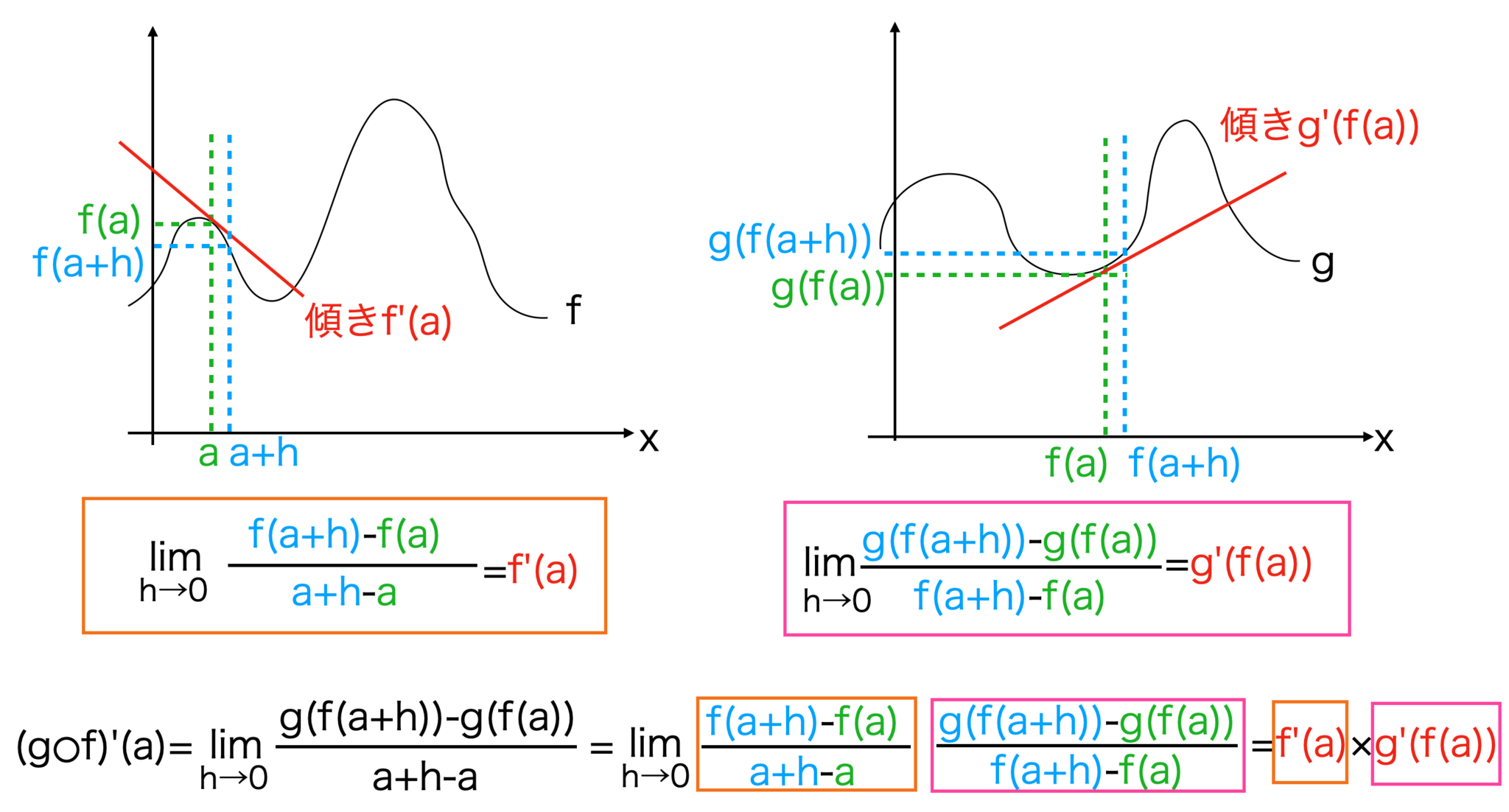合成関数の微分の式のイメージ