[超解説] 13の8乗を平方数2つの和で4通りに表わせ
$13^8$ を平方数 $2$ つの和で $4$ 通りに表わせ
平方数の和といえば
トートツですが、最も有名な平方数の和といえば「三平方の定理」ですよね。直角三角形において直角を挟む二辺の長さをそれぞれ二乗して足すと斜辺の長さの二乗に等しくなるというアレです。
三平方の定理の証明方法は無数にありますが、恐らく多くの方がこの定理を「平面図形上の性質」だと理解されておられるかと思います。もちろんその通りではあるのですが、数の世界というのは図形の世界の写像とみることもできるため、例えばこの記事のタイトルにあるような整数問題にも応用可能なんです。私の過去記事にも何度か登場している「ガラパゴ数学」というのはまさにそのような視点から生み出されたもので、それを用いると表題の問題が
に解けちゃうよっていうテーマで送りしたいと思います(*´∀`*)
まずは基礎知識として三平方の定理について改めて見直してみましょう。
三平方の定理 featuring ガラパゴ数学
三平方の定理というのは、数の世界でいうところの絶対値を表す定理でもあります。難しい言葉でいえば「ユークリッドノルム」ですね。
$$\Huge\quad\quad|a+bi|^2=a^2+b^2$$
絶対値記号の定義に従えばこのように解釈できますが、その本質にあるのが三平方の定理で、実際、絶対値記号の「定義」というのは先程の「数の世界は図形の世界からの写像」という視点を用いれば「定理」として導くことができるんです。実際にやってみましょう。
まず、定義ありきによる循環論法を封印するため、原点 $0$ から $a+bi$ で指し示される座標までの距離 $|a+bi|$ を $c$ とおきます。$a$ と $b$ の大きさはわかっていますが、複素平面上の $0,~a,~a+bi$ あるいは $0,~a,~a-bi$ で作られる直角三角形の斜辺の長さである $c~(=|a+bi|=|a-bi|)$ の具体値は現時点で不明です。
ここでおもむろに $(a+bi)\times(a-bi)$ という掛け算を考えます。掛け算というと、小学校では「足し算の繰り返し」として習った方もおられると思いますがそれは整数倍としての一側面にすぎなくて、数と図形の世界を同一視して捉えるならば
「$0$ の位置」が同じで「$0$ から $+1$ へ向かう向きと大きさ」が異なる
二つのユークリッド座標系 $\mathbb{A}$ と $\mathbb{B}$ において、
「$\mathbb{A}$ の量(座標) $a$ が $\mathbb{B}$ の量(座標)の $+1$」であるとき、
「$\mathbb{B}$ の量(座標) $b$ は $\mathbb{A}$ の量(座標)の $a\times b$」
というのが乗算の根本原理として視えてきます。このあたりについては数学を愛する会 Wiki の ガラパゴ数学 の演算の項に四則演算の捉え方としてまとめてありますのでご参考までに(*´ω`*)
さて、改めましてこの視点で $(a+bi)\times(a-bi)$ を考えるとどうなるでしょうか。まず2つの座標系 $\mathbb{A}$ と $\mathbb{B}$ を考えます。これらの座標系は $0$ つまり原点の座標が同じなのですが縮尺や姿勢(座標系全体の傾き)は必ずしも同じとは限らなくて、判明しているのは $\mathbb{A}$ の量(座標)の $(a+bi)$ が $\mathbb{B}$ の量(座標)の $+1$ で $\mathbb{B}$ の量(座標)の $(a-bi)$ が $\mathbb{A}$ の量(座標)の $(a+bi)\times(a-bi)$ ということです。
$a+bi$ や $a-bi$ というのは $1$ と $i$ を基底の元とする二次元の直交座標系上の数ですので、基準となる $1$ に相当する量(座標)とそれに直交する $i$ に相当する量(座標)を対応させてみると $2$ つの座標系の相互翻訳がしやすくなります。
というわけで、2つの座標系の対応表はこんな感じです。
| 座標系 | 基準座標 | 基準量 | 総量 |
|---|---|---|---|
| $\mathbb{A}$ | $0$ | $a+bi$ | $(a+bi)\times(a-bi)$ |
| $\mathbb{B}$ | $0$ | $1$ | $a-bi$ |
↓ ↓ ↓
| 座標系 | 原点 | 基準1 | 基準2 | 総量 | ||
|---|---|---|---|---|---|---|
| $\mathbb{A}$ | $0$ | $a+bi$ | $-b+ai$ | $a^2+abi$ | $b^2-abi$ | $a^2+b^2+0i$ |
| $\mathbb{B}$ | $0$ | $1$ | $i$ | $a$ | $-bi$ | $a-bi$ |
うん、確かに $a^2+b^2$ は出てきたけども、これは一体何を計算したのと疑問を持たれたかもしれません。でもこれ、図形として絵に描いてみると対応表の意味が分かってくるかと思います。
 三平方の定理その1
三平方の定理その1
相似の直角三角形がいくつか視えてこないでしょうか?赤い線は $\mathbb{B}$ の直交座標系を表した補助線となっていて、緑の線は相似の直角三角形を示しています。最初に想定した三辺の長さが $a,~b,~c$ の 直角三角形の大きさを $1$ としたとき、$1:a$、$1:b$、$1:c$ の相似比の直角三角形がそれぞれ視えたなら大成功! であれば、その中の $1:c$ の直角三角形の斜辺が $c^2$ になることは自明ですから、$c^2=|a+bi|^2=a^2+b^2$ は定理として成立しています。
ピタゴラス比 featuring ガラパゴ数学
さきほど計算したのは $(a+bi)\times(a-bi)$ でしたが、これを $(a+bi)\times(a+bi)$ で考えてみましょう。
| 座標系 | 原点 | 基準1 | 基準2 | 総量 | ||
|---|---|---|---|---|---|---|
| $\mathbb{A}$ | $0$ | $a+bi$ | $-b+ai$ | $a^2+abi$ | $-b^2+abi$ | $a^2-b^2+2abi$ |
| $\mathbb{B}$ | $0$ | $1$ | $i$ | $a$ | $bi$ | $a+bi$ |
$c=|a+bi|=|a-bi|$ ですから、$|(a+bi)(a-bi)|$ と $|(a+bi)^2|$ は同じ大きさのはず。つまり $|a^2-b^2+2abi|=a^2+b^2$ といえるはずです。実際、$\sqrt{(a^2-b^2)^2+(2ab)^2}=\sqrt{(a^2+b^2)^2}$ となることからも「それはそう」案件ではあるのですが、計算結果からではなく絵からご確認いただきましょう。
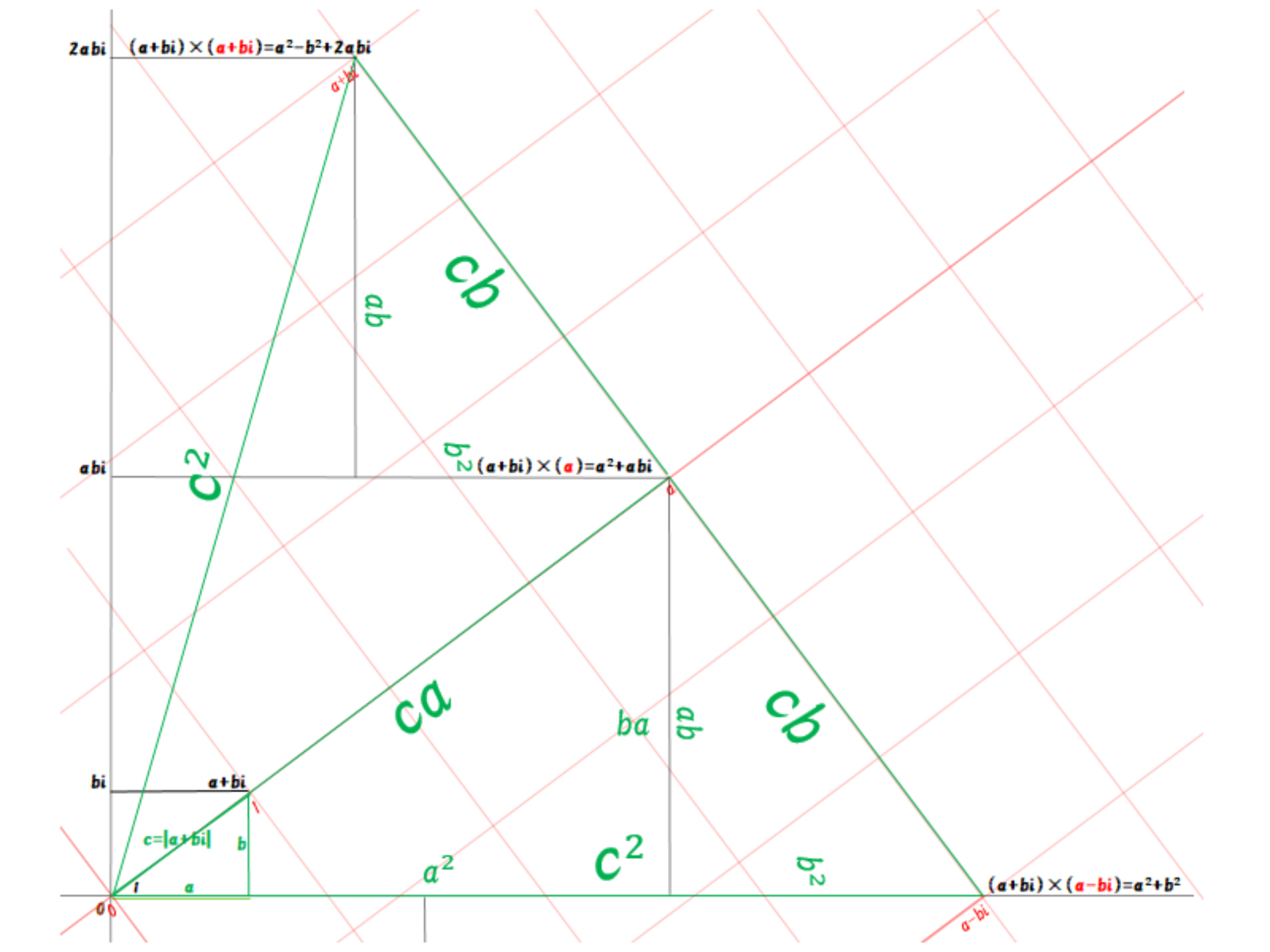 三平方の定理その2
三平方の定理その2
さらにこの図の $a^2-b^2+2abi$ から一番下まで垂線を下ろすと、「最初の直角三角形の鋭角を2倍した角度」を鋭角に持つ新たな直角三角形が視えてきます。その三辺の長さは $a^2-b^2,~2ab,~a^2+b^2$ と表せますので、もし $a$ と $b$ が整数であれば三辺とも整数比の直角三角形になるわけです。つまり、この手法を用いれば「ピタゴラス比」の三角形を自在に作れちゃうってワケ。
$|(a+bi)^2|=|(a^2-b^2)+(2ab)i|^2=a^2+b^2$
$\Large\Downarrow$
$a^2-b^2:2ab:a^2+b^2$
というわけで、整数比の直角三角形は、「直角を挟む二辺が整数比の直角三角形の鋭角を2倍した角度」を持つ直角三角形を作ることで無限に作り出すことが可能です。
$13^8$ を平方数 $2$ つの和で $4$ 通りに表わせ
さて、いよいよ表題のトピックに入りたいと思います。この問題は何年か前に「数学を愛する会(通称:ますらば)」の自作問題チャンネルにて会員の 天真 さんより出題されたもので、想定解はブラーマグプタの二平方恒等式にあてはめるものと三角関数を使って解くというものでした。
私も最初はどうやって解くんだろうと考えてしまいましたが、しばらくしてガラパゴ数学の視点からスマートな解法をひらめき、以来何度となくこの問題を良問として取り上げさせていただいております。
その解法というのが、まさにここまで長々と解説させていただいた
$$|(a+bi)^2|=|(a+bi)(a-bi)|=a^2+b^2$$
を応用したものなんですね。では、さっそく解法にいってみましょう☆彡
まず、$13^8$ を素因数分解して絶対値の積の $2$ 乗の形を想定します。
$13^8=|\sqrt{13}\cdotp\sqrt{13}\cdotp\sqrt{13}\cdotp\sqrt{13}\cdotp\sqrt{13}\cdotp\sqrt{13}\cdotp\sqrt{13}\cdotp\sqrt{13}|^2$
ここでもし絶対値が $\sqrt{13}$ となるような複素数がみつかるのであれば、その数で代用してあげればよいわけです。「フェルマーの二平方定理」によると、素数かつ $4$ で割ると $1$ 余るような整数は必ず平方数の和で表せるとのことなので、単純に偶数 $2m$ と奇数 $2n+1$ をそれぞれ平方した和を考えればオッケー。
$$\sqrt{(2m)^2+(2n+1)^2}=\sqrt{4(m^2+n^2+n)+1}$$
$m^2+n(n+1)=\frac{13-1}4=3$ となるような非負整数 $m,~n$ を見つければ$\textcolor{#a03}{\mathrm{BINGO!!}}$なのですが、$3$ より小さい平方数は限られてますから、$m=1,~n=1$ からの $\sqrt{2^2+3^2}=\sqrt{13}$ がすぐに見つかります。
すると、このとき想定される $\sqrt{13}$ は
$$\begin{align} &|\pm(2+3i)|=|\pm(2-3i)|\\=&|\pm(3+2i)|=|\pm(3-2i)| \end{align}$$
と $8$ 通りあって、いずれも直角三角形の斜辺あるいは長方形の対辺としてみればそれらの二次元図形としての形状はすべて合同です。
ここで注目すべきは、それらを回転させたときに対辺の向きが同じものと逆になっているものがあって、同じ向き同士の積からは $(a+bi)^2=(a^2-b^2)+(2ab)i$ のように新たな直角三角形(あるいは長方形)が生み出され、逆向きのペアの積からは $(a+bi)(a-bi)=(a^2+b^2)+0i$ のように潰れて一次元状になってしまうってこと。
これは直角三角形の2つの鋭角の和が90度だということに起因していて、そのような性質を上手に操ればこの問題はベリーイージーになります。
具体的な方法ですが、先程の $8$ 通りからどれか一つ選んで
$$\begin{align} &|(2+3i)^8(2-3i)^0|^2=(2^2+3^2)^0|(2+3i)^8|^2=|~~~~-239+28560i|^2\quad\\ =&|(2+3i)^7(2-3i)^1|^2=(2^2+3^2)^1|(2+3i)^6|^2=|+26455-10764i|^2\quad\\ =&|(2+3i)^6(2-3i)^2|^2=(2^2+3^2)^2|(2+3i)^4|^2=|-20111-20280i|^2\quad\\ =&|(2+3i)^5(2-3i)^3|^2=(2^2+3^2)^3|(2+3i)^2|^2=|+10985-26364i|^2\quad\\ =&|(2+3i)^4(2-3i)^4|^2=(2^2+3^2)^4~~~~~~~~~~~~~~~~~~~=~+28561\quad\\ =&|(2+3i)^3(2-3i)^5|^2=(2^2+3^2)^3|(2-3i)^2|^2=|-10985-26364i|^2\quad\\ =&|(2+3i)^2(2-3i)^6|^2=(2^2+3^2)^2|(2-3i)^4|^2=|-20111+20280i|^2\quad\\ =&|(2+3i)^1(2-3i)^7|^2=(2^2+3^2)^1|(2-3i)^6|^2=|+26455+10764i|^2\quad\\ =&|(2+3i)^0(2-3i)^8|^2=(2^2+3^2)^0|(2-3i)^8|^2=|~~~~-239-28560i|^2\quad\\ \end{align}$$
という組み合わせを作るだけです。あ、今回選んだのはたまたま $(2+3i)(2-3i) $ の相殺ペアでしたが、どれを選んでも最終的に得られる結果は同じになりますよ ♪
中辺にみえる $(2^2+3^2)$ が左辺の中にある逆向きペアから生まれた一次元形状、つまり係数としてのスカラー値ですね。そして上 $4$ 行と下 $4$ 行にみる鏡写しペアも合同形ですので、実質的には上下いずれか $4$ 行分だけで答えは求まります。
というわけで、答えはこうなりますヽ(=´▽`=)ノ
$$\begin{align} |(2+3i)^8(2-3i)^0|^2=|~~~~-239+28560i|^2=~~~~239^2+28560^2=13^8\quad\\ |(2+3i)^7(2-3i)^1|^2=|+26455-10764i|^2=26455^2+10764^2=13^8\quad\\ |(2+3i)^6(2-3i)^2|^2=|-20111-20280i|^2=20111^2+20280^2=13^8\quad\\ |(2+3i)^5(2-3i)^3|^2=|+10985-26364i|^2=10985^2+26364^2=13^8\quad\\ \end{align}$$
最後までお読みいただき、ありがとうございました(*´∀`*)
