0
高校数学解説

ある曲線を近似

109
0
$$\newcommand{C}[2]{{{}_{#1}\mathrm{C}_{#2}}} \newcommand{floor}[1]{{\lfloor{#1}\rfloor}} $$

ある曲線を描くのが難しいので，描き慣れた直線と放物線でそれっぽいものを描きたい．そこで以下のものを考えた．

$0\leq x\leq\frac\pi 2$において
$$ \begin{cases} y=\frac3\pi x&\big(0\leq x\leq\frac\pi 6\big)\\ y=1-\frac9{2\pi^2}\big(x-\frac\pi2\big)^2&\big(\frac\pi6\leq x\leq\frac\pi2\big) \end{cases} $$

これは$y=\sin x$の部分的な近似である．グラフ作成ソフト(desmos)でプロットすると，

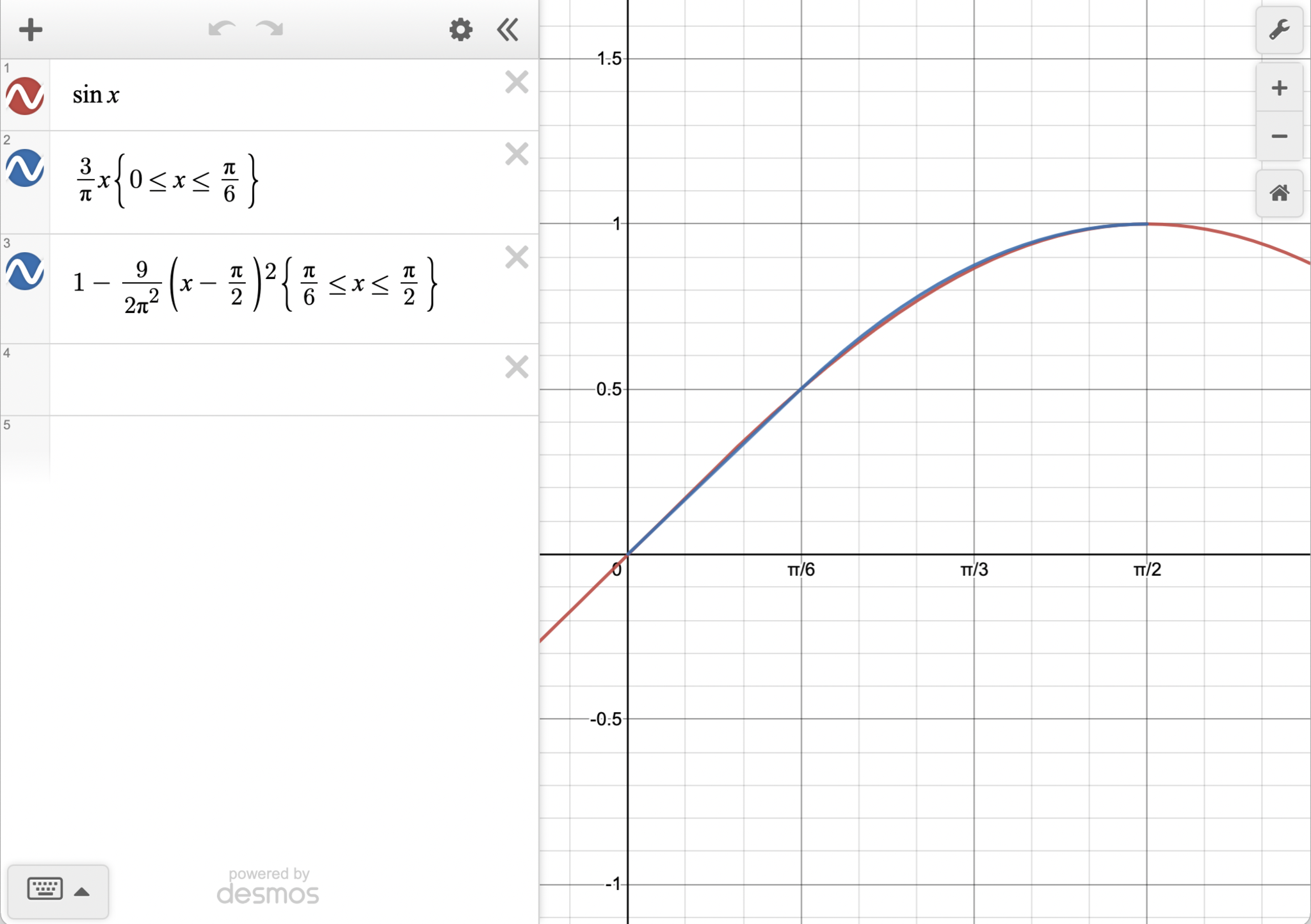graph graph

少し見づらいかもしれないが，そこそこの精度での近似ができている．その理由として，大学数学を用いると，

  • $y=\sin x$がTaylor展開により，
    　- $x=0$付近で$x$，
    　- $x=\frac\pi2$付近で$1-\frac12(x-\frac\pi2)^2$
    と近似され，また$\frac3\pi\simeq1$
  • $0< x<\frac\pi2$全域において導関数が存在してそれが連続

であることが挙げられる．

投稿日：2021年3月21日

この記事を高評価した人

高評価したユーザはいません

この記事に送られたバッジ

バッジはありません。

投稿者

しゅどぼ
しゅどぼ
11
297
自分用

コメント

他の人のコメント

コメントはありません。
読み込み中
しゅどぼ
しゅどぼ
ある曲線を近似