個人用

まさかの幾何

　こんにちは．まさか京大本レに幾何が出てくるとは思いませんでした．いろいろ考えたのですが，かなり知識が必要な解法しか思い浮かばなかったのでMathlogに軽くまとめておきます．

Step1:答から逆算

　とりあえず図を書いてみましょう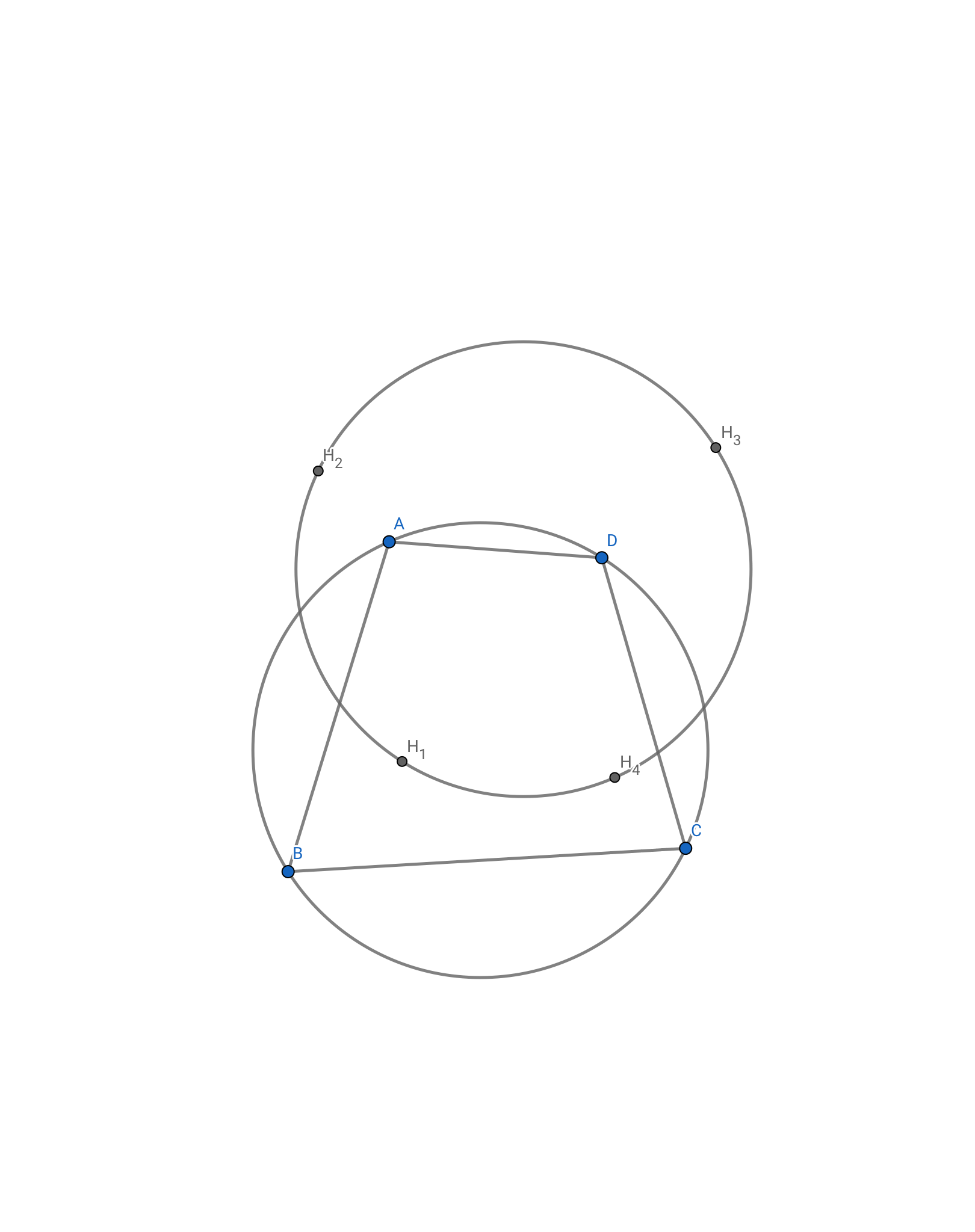． とりあえず図をかいてみた
　何が使えそうだか考えてみます．今回は角度で見るのが良さそうなので，円周角の定理か内角の和が$180^\circ$になることを使いたいです．

Step2:既存の知識を用いる(ここが鬼畜)

　ここから先は知ってるか知らないかなんですけど，$\mathrm{H}_1\mathrm{H}_4\parallel\mathrm{A}\mathrm{D},\mathrm{H}_1\mathrm{H}_2\parallel\mathrm{C}\mathrm{D},\mathrm{H}_2\mathrm{H}_3\parallel\mathrm{BC},\mathrm{H}_3\mathrm{H}_4\parallel\mathrm{A}\mathrm{B}$が成立します．ちなみに，数学オリンピックを経験していない人達がこれに気づくのは難しいです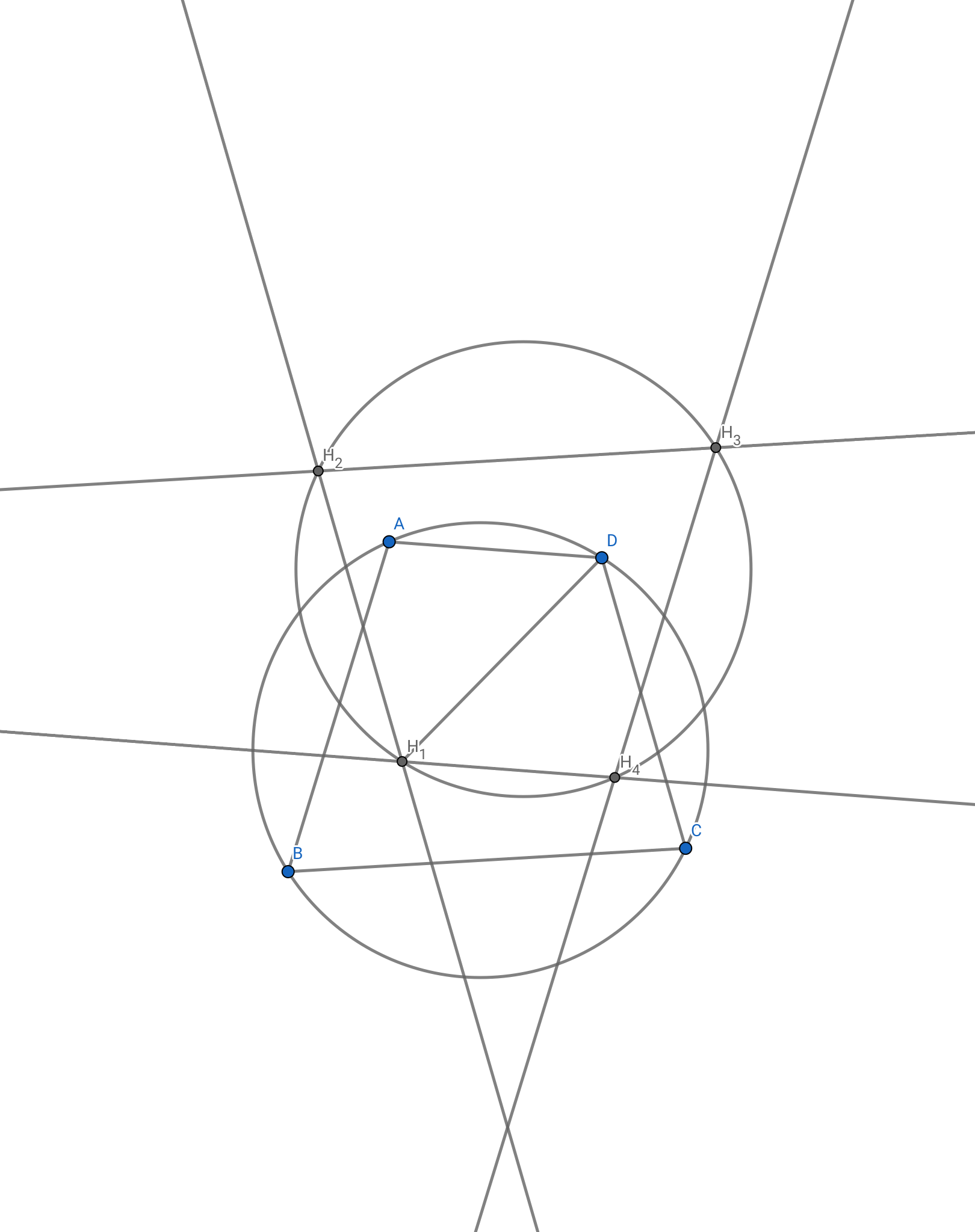． こんなの誰が知ってるんですか
　あとは錯角を使うと
\begin{align*} \angle\mathrm{H_1DC}&=\angle\mathrm{H_2H_1D}\\ \angle\mathrm{ADH_1}&=\angle\mathrm{DH_1H_4}\\ \therefore \angle\mathrm{H_2H_1H_4}&=\angle\mathrm{ADC} \end{align*}
　同様にして$\angle\mathrm{H_1H_4H_3}=\angle\mathrm{BAD},\angle\mathrm{H2H_2H_3}=\angle\mathrm{BCD},\angle\mathrm{H_2H_3H_4}=\angle\mathrm{ABC}$が示せるので，四角形$\mathrm{ABCD}$と四角形$\mathrm{H_1H_2H_3H_4}$は相似となります．四角形$ABCD$は外接円を持つので，もちろん四角形$\mathrm{H_1H_2H_3H_4}$も外接円を持ちます．よって$4$点$\mathrm{H_1,H_2,H_3,H_4}$は同一円周上に存在することが示されました．

最後に

　京大の幾何の問題はたいてい難しいのですが，今回の東進京大本レのこの問題はあまりにも難しいと思います．ぼくは数学オリンピック対策でこういう感じの幾何をたくさんやってきているのでまだ慣れていますが，これを文系の受験生にやらせるのは違う気がします．本番の幾何問題よりも難しいです．解けなくても気にしなくて良いと思いました．