☆ 和積の公式のビジュアルイメージ ☆

和積の公式ってなんだっけ

三角関数の和積の公式というのは、三角関数同士の和を三角関数同士の積で表しちゃう公式です。
$$\begin{cases} \displaystyle\cos x+\cos y~=~~~2\cos\frac{x-y}2\cos\frac{x+y}2\\ \displaystyle\sin x~+\sin y~=~~~2\cos\frac{x-y}2\sin\frac{x+y}2\\ \displaystyle\cos x-\cos y~=-2\sin\frac{x-y}2\sin\frac{x+y}2\\ \displaystyle\sin x~-\sin y~=~~~2\sin\frac{x-y}2\cos\frac{x+y}2\\ \end{cases}$$

私自身、大抵のことは複素数やその実部虚部で求めてしまうのであんまり三角関数の公式とかは覚えてないのですが、そんな私がこれらの公式を一体どういう視点で捉えているのか、ビジュアルイメージを交えて翻訳致しましょう。

和積の公式を描いてみた

まず、$[\cos x+i\sin x]+[\cos y+i\sin y]~(=e^{ix}+e^{iy})$ の図をイメージします。
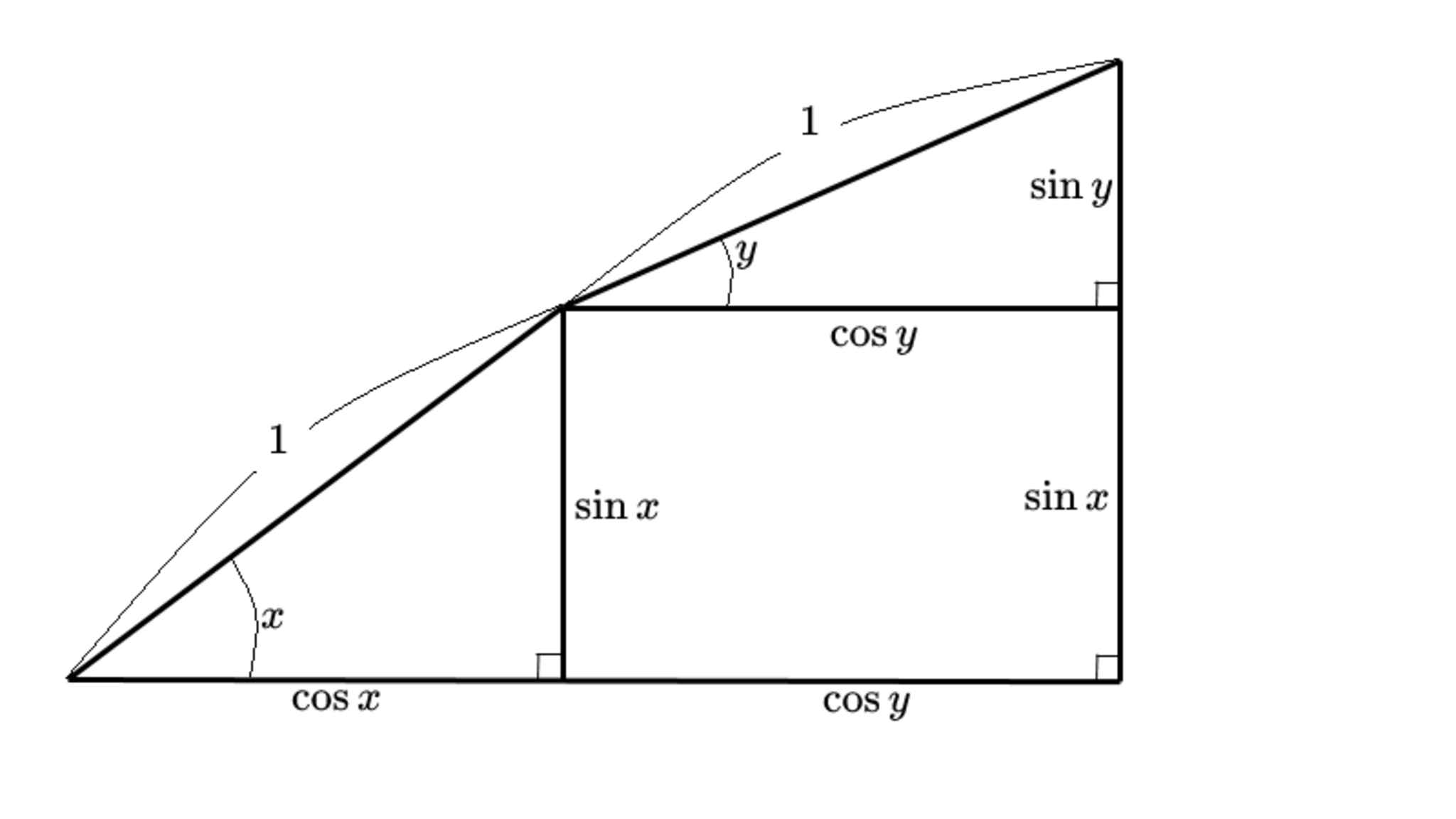STEP1

すると、二等辺三角形が視えてきました。
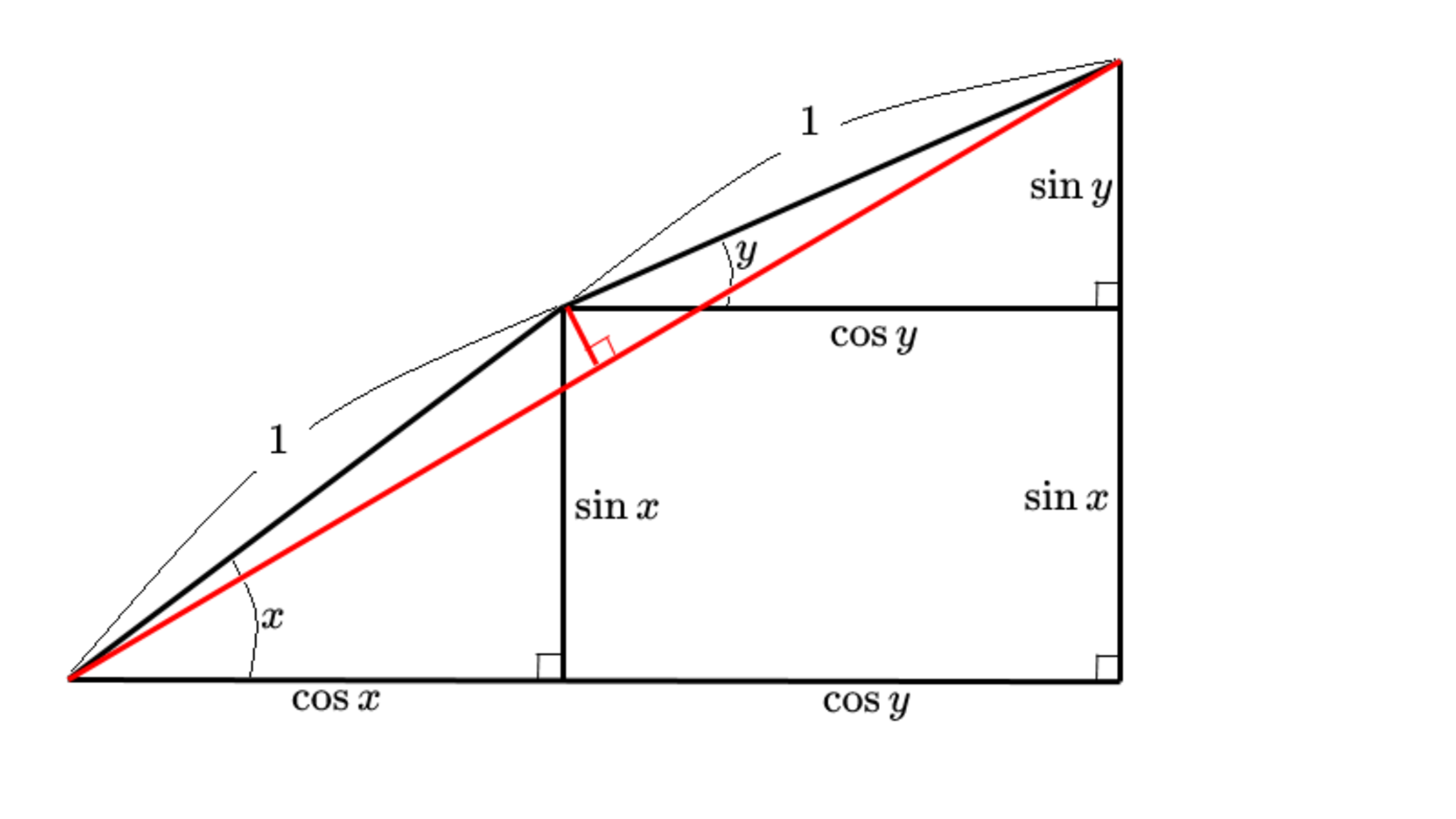STEP2

図より二等辺三角形の頂角は $\pi-x+y$ ですね。
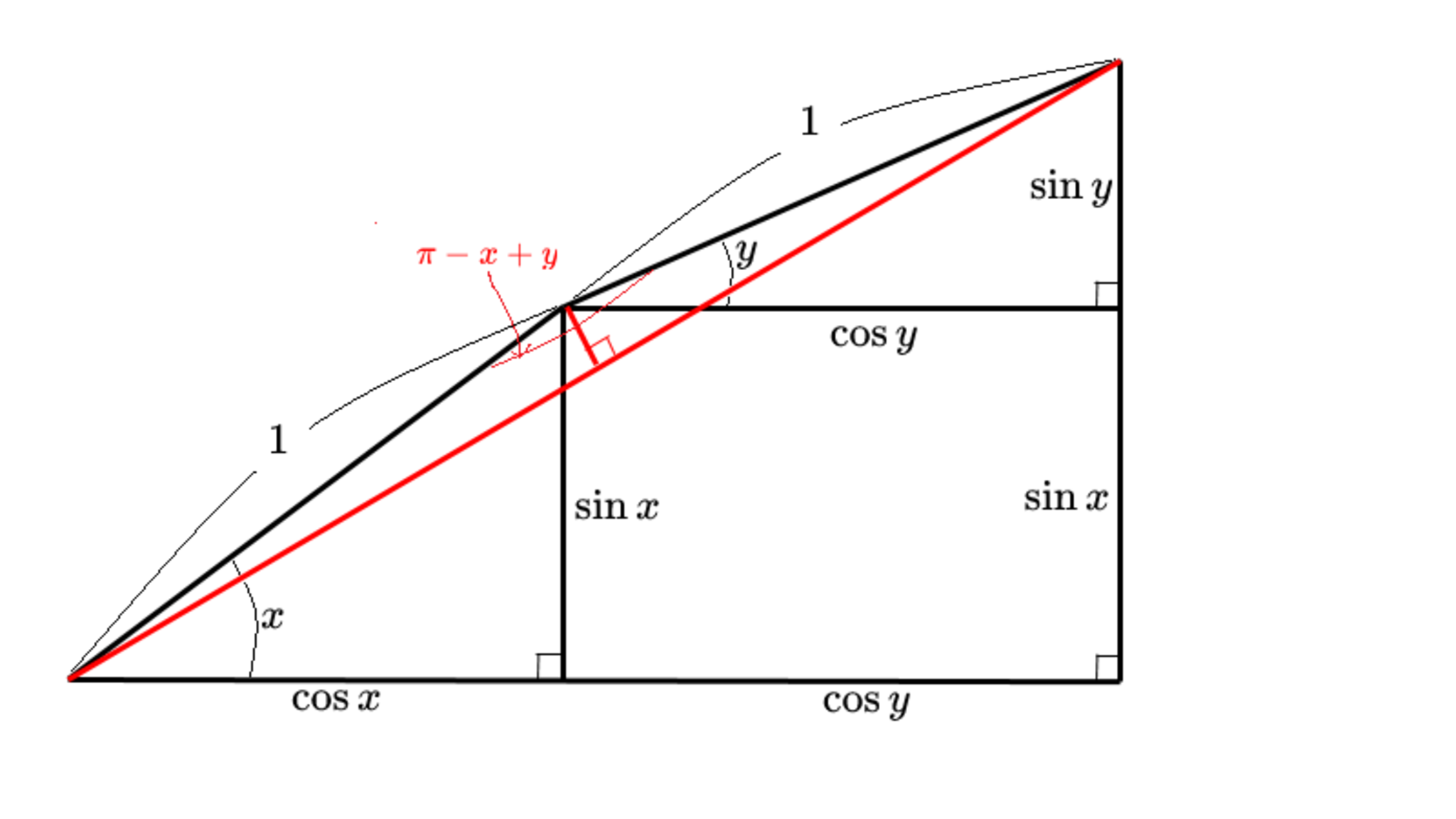STEP3

ということは二等辺三角形の底角は $\frac{x-y}2$ です。
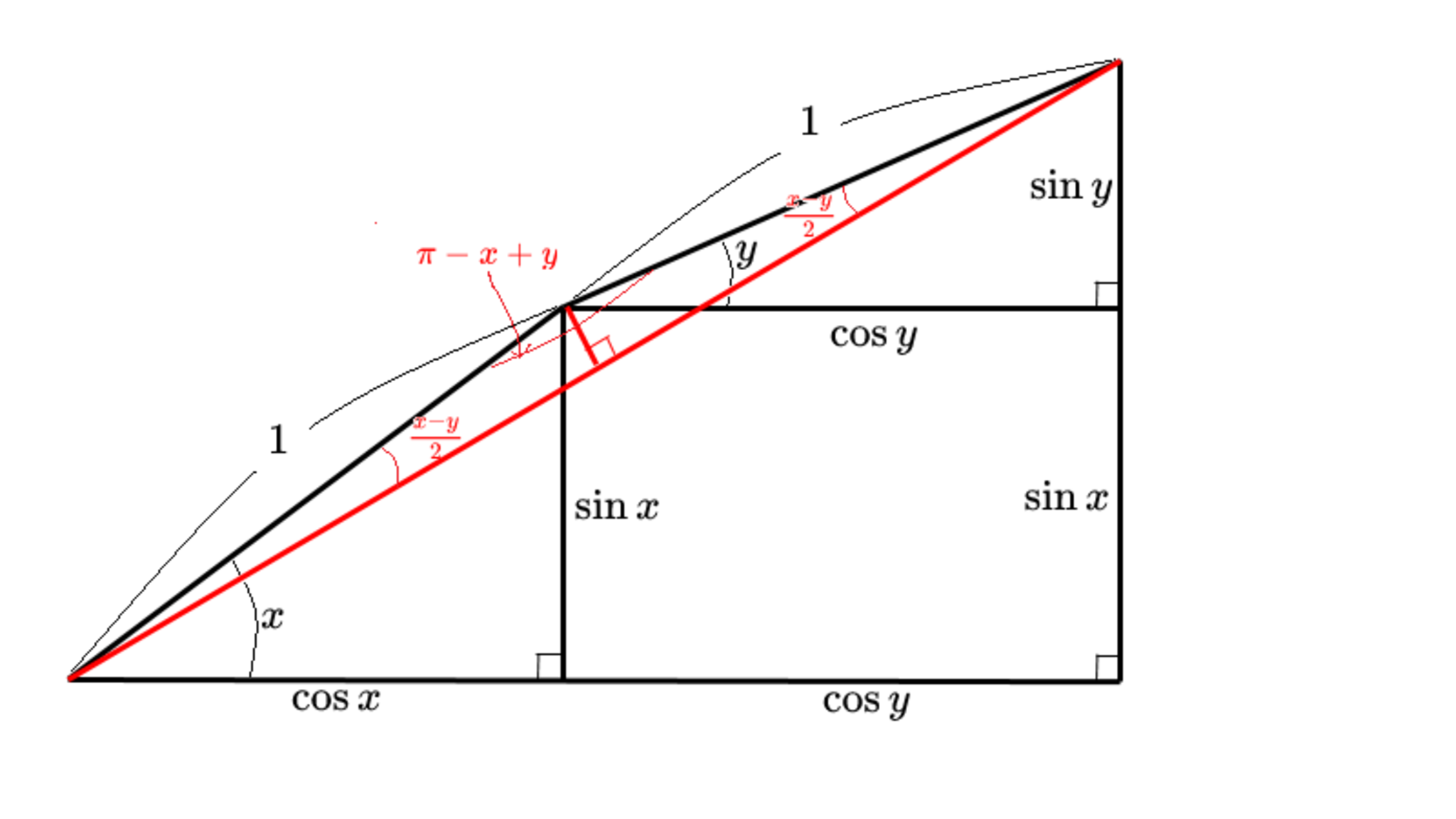STEP4

二等辺三角形の底辺の長さは $\cos\frac{x-y}2+\cos\frac{x-y}2$ です。
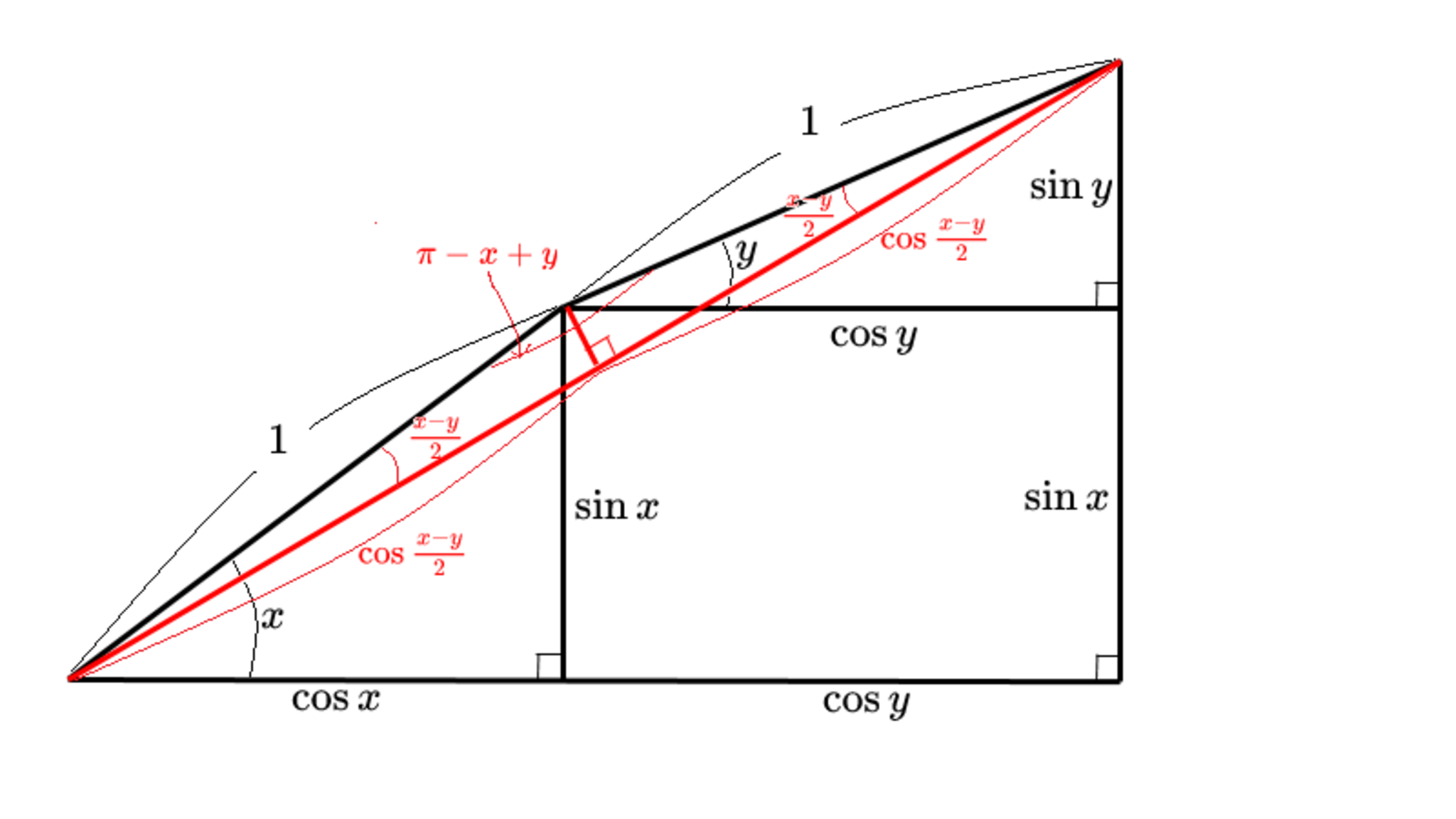STEP5

斜辺が $2\cos\frac{x-y}2$ な直角三角形が視え、その鋭角が $\frac{x+y}2$ なので$\cdots$ あとはお察し！
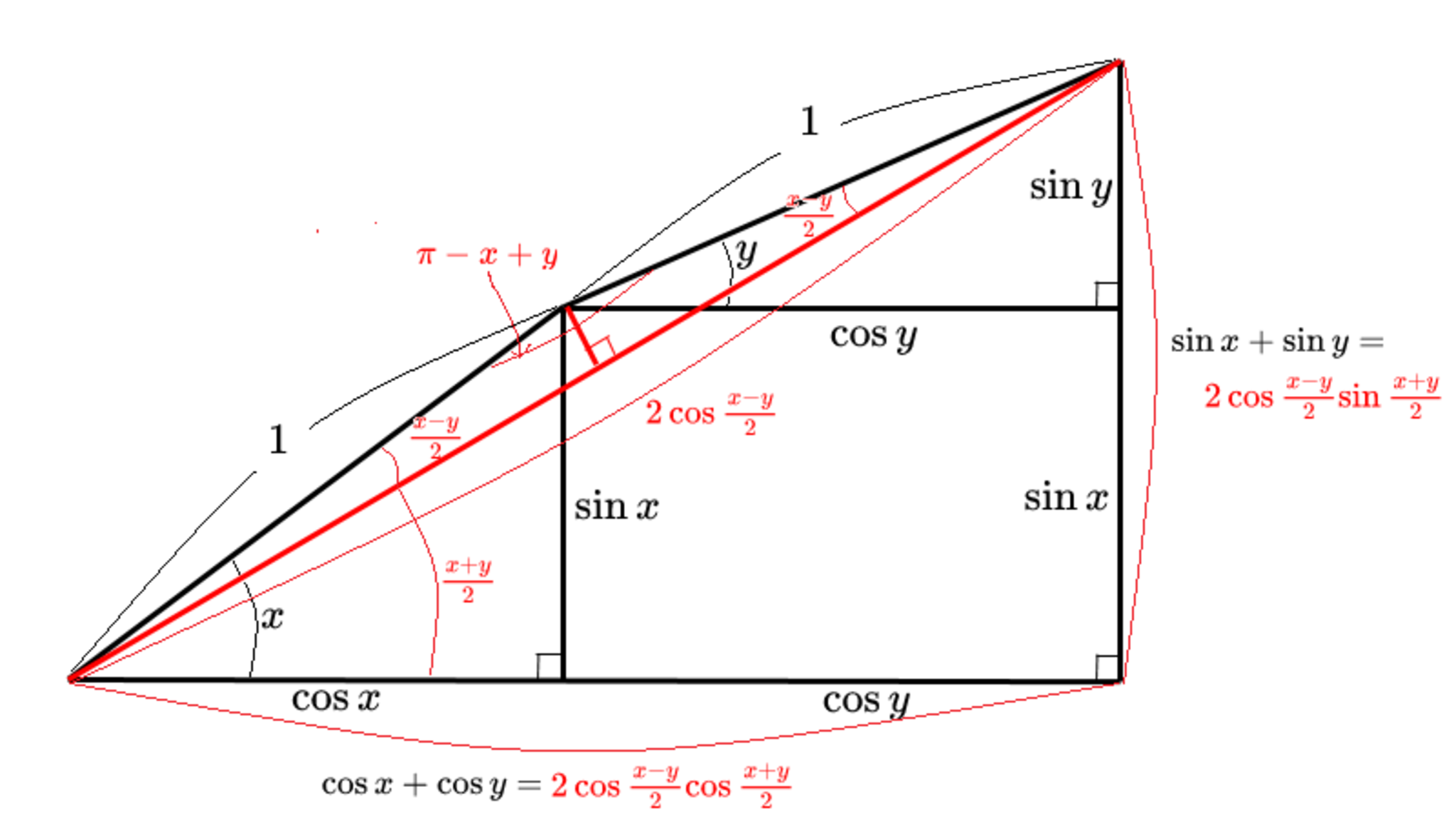STEP6

差積の公式を描いてみた

まず、$[\cos x+i\sin x]-[\cos y+i\sin y]~(=e^{ix}-e^{iy})$ の図をイメージします。
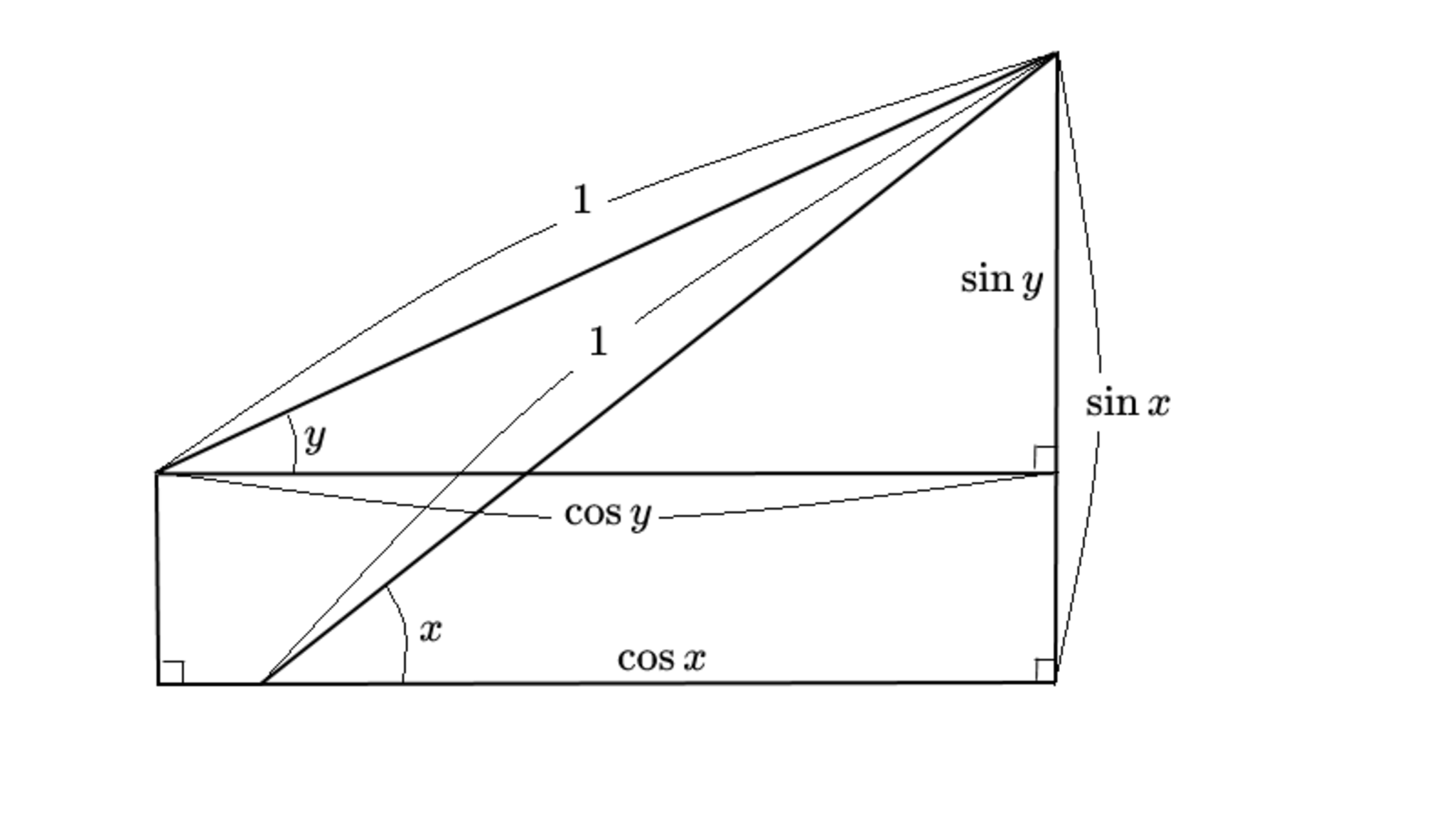STEP1

すると、二等辺三角形が視えてきました。
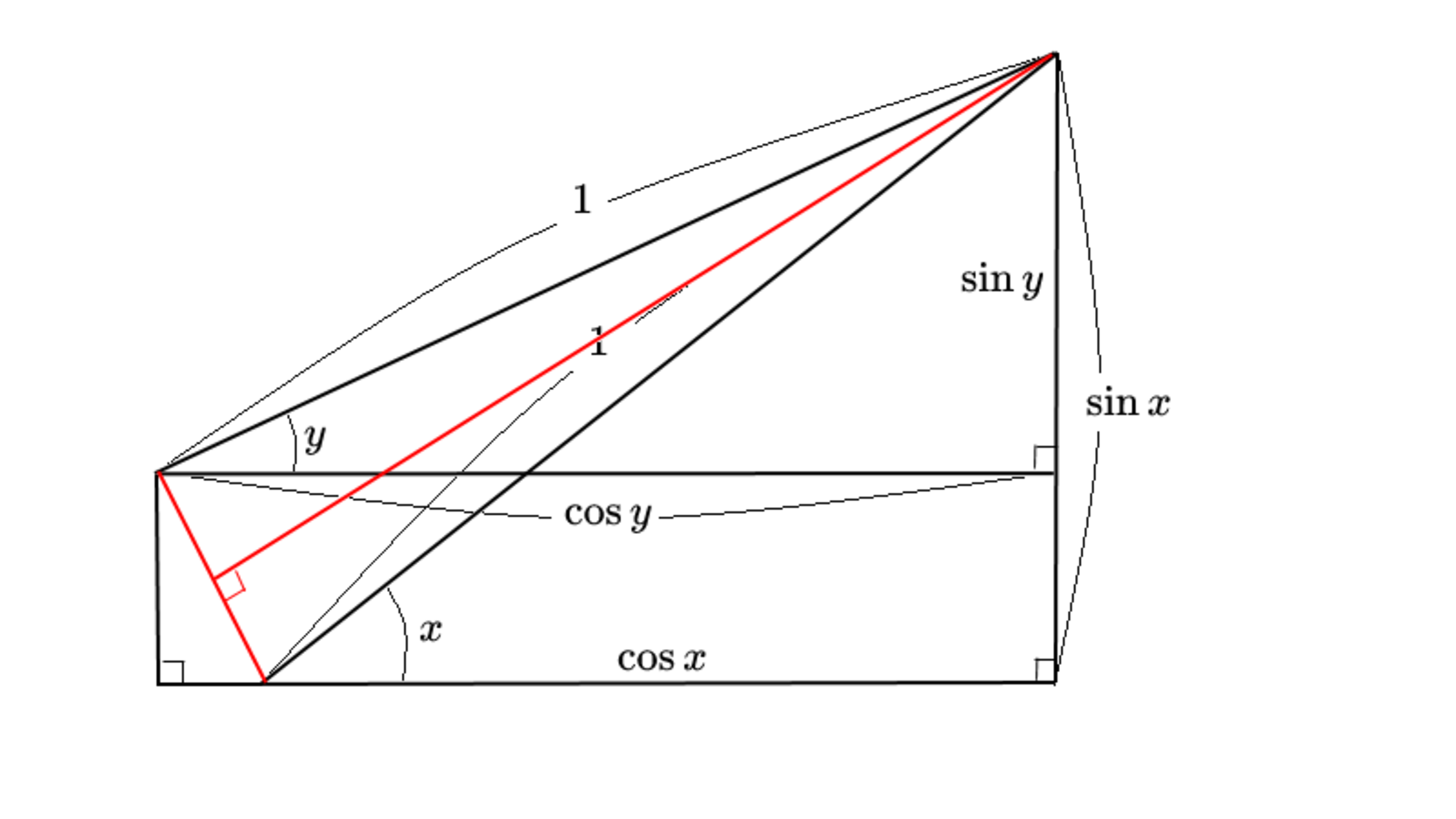STEP2

図より二等辺三角形の頂角は $x-y$ ですね。
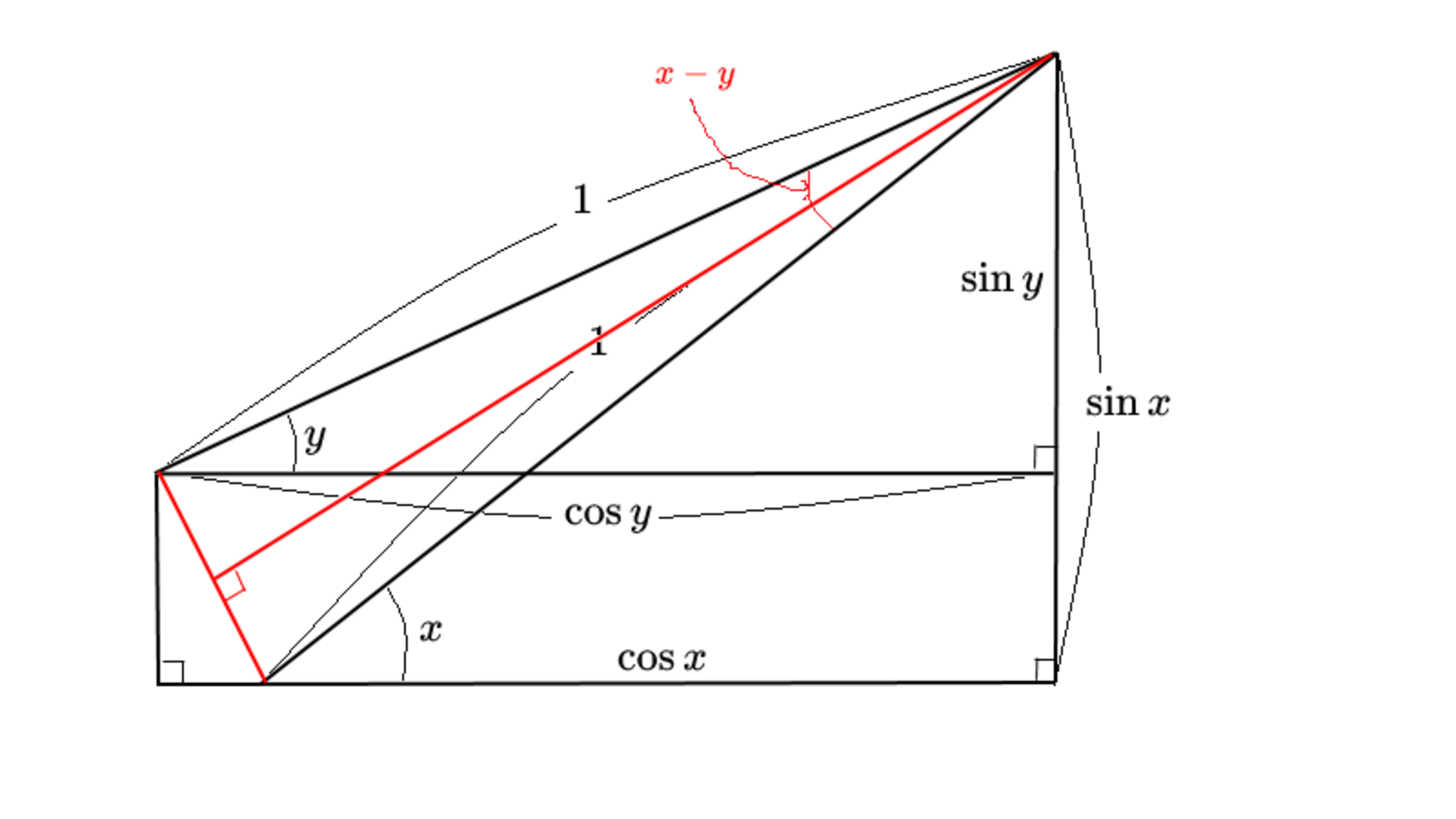STEP3

二等辺三角形の頂角の半分は $\frac{x-y}2$ です。
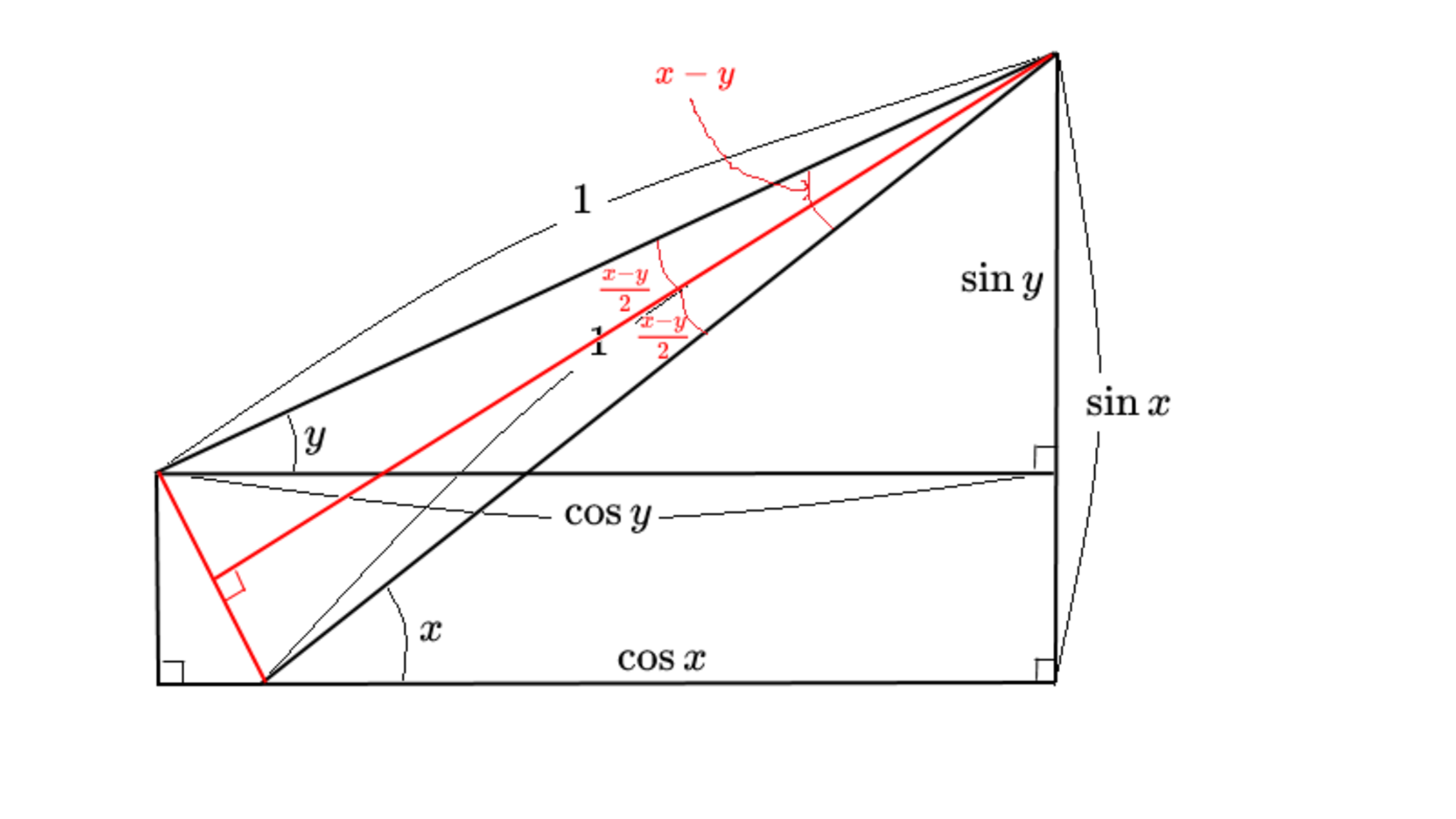STEP4

二等辺三角形の底辺の長さは $\sin\frac{x-y}2+\sin\frac{x-y}2$ です。
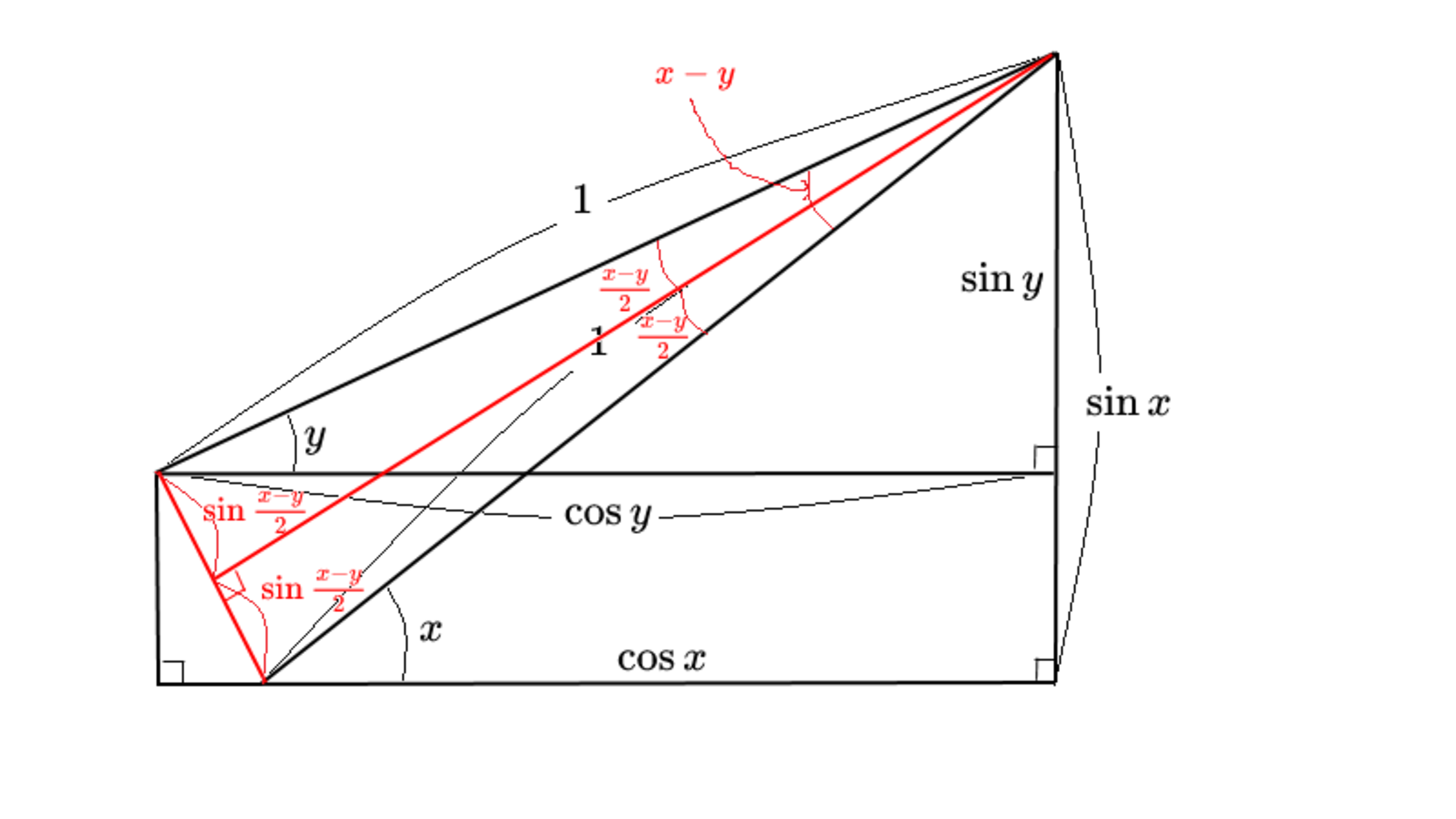STEP5

斜辺が $2\sin\frac{x-y}2$ な直角三角形が視え、その鋭角が $\frac{x+y}2$ なので$\cdots$ あとはお察し！
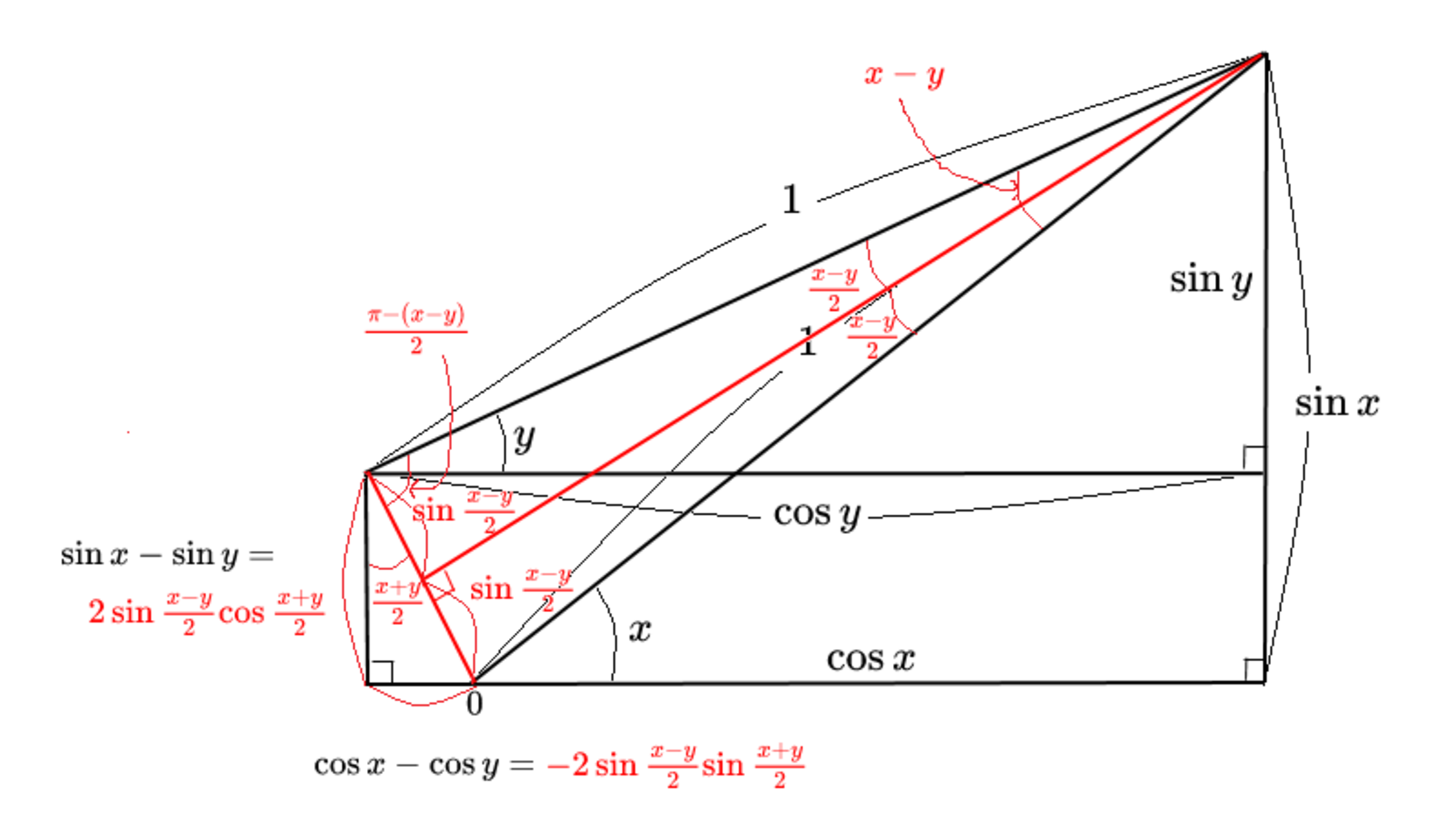STEP6

数式で解説！！

ここまでのイメージを数式で書くとこーなります。

$$\begin{align} &(\cos x+\cos y)+i(\sin x+\sin y)\\ =&(\cos x+i\sin x)+(\cos y+i\sin y)\\ =&e^{ix}+e^{iy}\\ =&\underbrace{\left(e^{\frac{x-y}2i}+e^{-\frac{x-y}2i}\right)}_{複素共役同士の和}\left(e^{\frac{x+y}2i}\right)\\ =&\underbrace{\left(2\cos\frac{x-y}2\right)}_{複素共役同士の和}\left(\cos\frac{x+y}2+i\sin\frac{x+y}2\right)\\ =&\left(2\cos\frac{x-y}2\cos\frac{x+y}2\right)+i\left(2\cos\frac{x-y}2\sin\frac{x+y}2\right) \end{align}$$

$$\begin{align} &(\cos x-\cos y)+i(\sin x-\sin y)\\ =&(\cos x+i\sin x)-(\cos y+i\sin y)\\ =&e^{ix}-e^{iy}\\ =&\underbrace{\left(e^{\frac{x-y}2i}-e^{-\frac{x-y}2i}\right)}_{複素共役同士の差}\left(e^{\frac{x+y}2i}\right)\\ =&\underbrace{\left(2i\sin\frac{x-y}2\right)}_{複素共役同士の差}\left(\cos\frac{x+y}2+i\sin\frac{x+y}2\right)\\ =&\left(-2\sin\frac{x-y}2\sin\frac{x+y}2\right)+i\left(2\sin\frac{x-y}2\cos\frac{x+y}2\right) \end{align}$$

オマケ

掛け算 $A\times B=C$ というのは「原点が同じで $A$ を $1$ とする座標系」において $B$ が示すのは、元の座標系における $C$ ですよという意味です（ ガラパゴ数学 視点）。このような乗算の本質を抑えると、複素数同士の掛け算はこんな風にビジュアルイメージすることが可能になります。

[加法定理]
$$\left(\cos\alpha+i\sin\alpha\right)\left(\cos\beta+i\sin\beta\right)=\left(\cos\alpha\cos\beta-\sin\alpha\sin\beta\right)+i\left(\cos\alpha\sin\beta+\sin\alpha\cos\beta\right)$$

[倍角の公式]
$$\begin{align}\left(\cos\alpha+i\sin\alpha\right)^2=&\left(\cos^2\alpha-\sin^2\alpha\right)+i\left(2\cos\alpha\sin\alpha\right)\\ =&\left(2\cos^2\alpha-1\right)+i\left(2\cos\alpha\sin\alpha\right)\\ =&\left(1-2\sin^2\alpha\right)+i\left(2\cos\alpha\sin\alpha\right)\\ \end{align}$$

[３倍角の公式]
$$\begin{align}\left(\cos\alpha+i\sin\alpha\right)^3 =&\left(\cos^2\alpha-3\sin^2\alpha\right)\cos\alpha+i\left(3\cos^2\alpha-\sin^2\alpha\right)\sin\alpha\\ =&\left(4\cos^2\alpha-3\right)\cos\alpha+i\left(3-4\sin^2\alpha\right)\sin\alpha\\ =&\left(4\cos^3\alpha-3\cos\alpha\right)+i\left(3\sin\alpha-4\sin^3\alpha\right)\\ \end{align}$$