【必勝法】ウサギと猟犬
ウサギと猟犬とは、任天堂のゲーム『世界のアソビ大全51』に収録されたボードゲームの一種です。
ここではこのゲームに関する定理、必勝法を記述します。
（必勝法と言いながら未解決なことをお詫び申し上げます。）
【リンク】
Nintendo Switch | 任天堂
世界のアソビ大全51 収録ゲーム
Amazon 世界のアソビ大全51
ルール説明
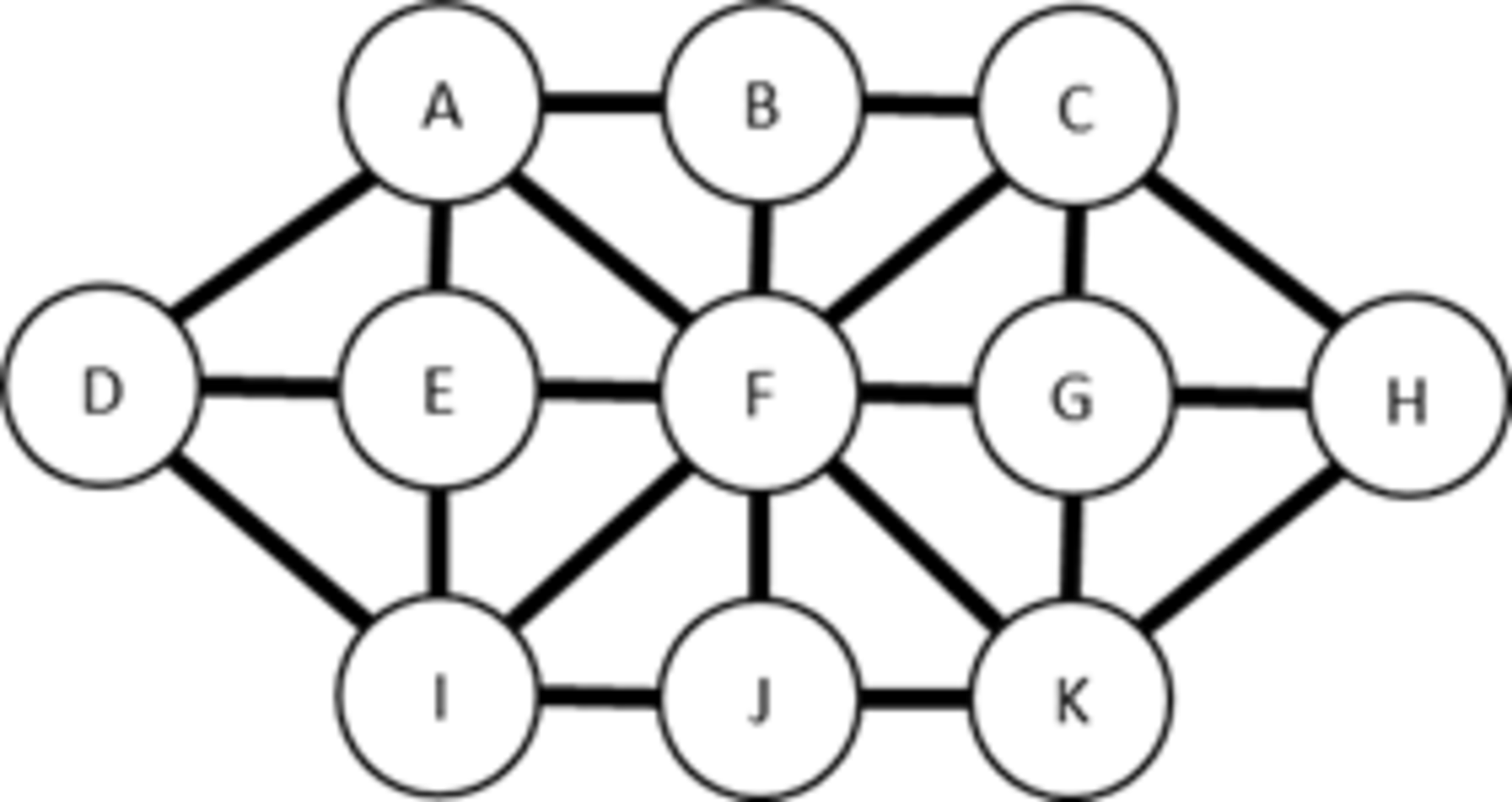ウサギと猟犬 盤面
上記の盤面を用意する。
※文字は説明のために置いたものであり、ゲームでは非表示
ルール
- プレイヤーを2人用意し、ウサギ、犬を操作するプレイヤーを決定する。
- 犬を上図のA、D、Iに配置し、ウサギをHに配置する。
向きは、犬はDからH方向、ウサギはHからD方向に向ける。
※ウサギをランダムに配置するルールもあるが、ここでは考慮しない。 - 先攻、後攻を決める。
- プレイヤーがコマを1マス動かし、プレイヤーのターンを交代する。
- ウサギは線でつながったマスを自由に移動できる。
犬は縦移動ができるが、後ろに下がることはできない。
また、犬は同じマスに2つ以上配置することはできない。
（例えば、ウサギはFから8方向に移動が可能だが、犬はFから、F→B、F→C、F→Gは移動できるが、F→A、F→E、F→Iは移動できない。）
ウサギの勝利条件
- A、D、Iのいずれかのマスに移動したとき。
- 前方に犬が1匹もいないとき。
（すべての犬がウサギの真横または後方にいる。） - ウサギ、犬のターンが合計30ターン経過したとき。
犬の勝利条件
次のターン、ウサギが動けなくなったとき。
つまり、犬が勝利する盤面は上下対称を同一視すると2パターンあり、
- 犬がA、F、CかつウサギがBにいるとき。
- 犬がC、G、KかつウサギがHにいるとき。
定理
ウサギがFにいるかつウサギのターンのとき、前方に少なくとも犬が3匹いなければウサギの勝利
ウサギと猟犬 盤面
ウサギがFにいるとし、ウサギのターンとする。
- ウサギの前方に犬がいない場合
この時点でウサギの勝利 - ウサギの前方に犬が1匹いる場合
犬がAにいない場合、ウサギはF→Aとすると勝利
犬がAにいる場合、ウサギはF→Iとすると勝利 - ウサギの前方に犬が2匹いる場合
A、E、Iにおいて、犬がいないマスが必ず1マス存在し、そのマスをXとすると
ウサギF→Xとすると勝利
1.2.3.から、ウサギの前に犬が3匹いなければウサギの勝利
ウサギは自身が敗北しないような最善手で行動した場合、犬は犬の勝利条件1.で勝利することはない。
ウサギと猟犬 盤面
以下、犬がA、D、I、ウサギがHにいる場合、(A,D,I|H)と表記する。
犬の勝利条件1.となる盤面を想定し、矛盾を導く。
犬の勝利盤面を(A,F,G|B)とする。
その1つ前の盤面を(A,F,G|X)とすると、ウサギX→BとなるマスXは存在しない。
よって、犬のターンにより盤面(A,F,G|B)が作られたことがわかる。
- (A,F,G|B)の1つ前の盤面を(X,F,G|B)と仮定する。
1-1. X=Dのとき
(D,F,G|B)の1つ前の盤面でウサギはA→Bと移動する必要があるが、ウサギはAにいる時点で勝利するため矛盾。
1-2. X=Eのとき
1-1.と同様に矛盾。 - (A,F,G|B)の1つ前の盤面を(A,X,G|B)と仮定する。
2-1. X=Eのとき
(A,E,G|B)の1つ前の盤面でウサギはF→Bと移動する必要があるが、ウサギが最善手で動くと「ウサギ中心定理」により、ウサギはFにいる状態からウサギが勝利する移動が存在するため矛盾。
2-2. X=I、X=J、X=K、X=Gのとき
2-1.と同様に矛盾。 - (A,F,G|B)の1つ前の盤面を(A,F,X|B)と仮定する。
3-1. X=Hのとき
(A,F,H|B)の1つ前の盤面でウサギはC→Bと移動する必要があるが、ここでC→Gと移動すれば、犬の勝利条件1.があてはまることはなくなる。
3-2. X=Gのとき
(A,F,G|B)の1つ前の盤面でウサギはC→Bと移動する必要があるが、ここでC→Hと移動すれば、犬の勝利条件1.があてはまることはなくなる。
（上下対称の場合は省略）
1.2.3.から、ウサギは自身が敗北しないような最善手で行動した場合、犬は犬の勝利条件1.で勝利することはない。
ウサギと犬が最善手で行動した場合、下図のHの位置に犬が移動した時点で、犬は敗北する。
ウサギと猟犬 盤面
例えば、犬1=A、犬2=D、犬3=I、兎=Hの時
(A,D,I|H)と表記する
「犬の勝利条件定理」より、ウサギと犬が最善手で犬が勝利する盤面は(C,G,K|H)のみ。
しかし、ルールにより犬は後ろに下がることができないので、Hに犬がいると(C,G,K|H)とすることができず、犬の勝利が不可能となり、犬は敗北する。
ウサギ、犬が両者とも最善手で動いた場合、必ずウサギが勝利する。
カウンタ$n \in \mathbb{Z}/2\mathbb{Z}$を以下のように定義する。
- 先攻がウサギ⇒$n=1$
- 先攻が犬⇒$n=0$
- ウサギまたは犬のどちらかが斜め移動した場合、$nに+1$する操作を行う。
このとき「犬の勝利⇒$n=0$」が成り立つ
（これは対偶「$n=1$⇒犬は勝てない」を意味する。）
証明に挑戦しましたが、できませんでした。
申し訳ありません。（´；ω；‵）