定規だけで双曲線に接線を作図・定規とコンパスだけで双曲線の漸近線を作図

はじめに

この記事では、
①定規だけで双曲線に接線を作図する方法
②定規とコンパスだけで双曲線の漸近線を作図する方法
を紹介します。

定規だけで双曲線に接線を作図する方法

楕円や放物線への接線について

前提

平面上に双曲線と点$A$があります。この点$A$から双曲線へ接線を作図したいと思います。

双曲線と点$A$

方法1

方法1-手順1 直線を3本引き、交点を結ぶ

直線を３本引き、交点を結ぶ

方法1-手順2 新たな交点をつなぐ直線を引き、双曲線との交点を作図する

新たな交点をつなぐ直線を引き、双曲線との交点を作図する

方法1-手順3　双曲線の接線を引く

双曲線の接線を引く

これで完成です!

次に、別の方法を紹介します。

方法2

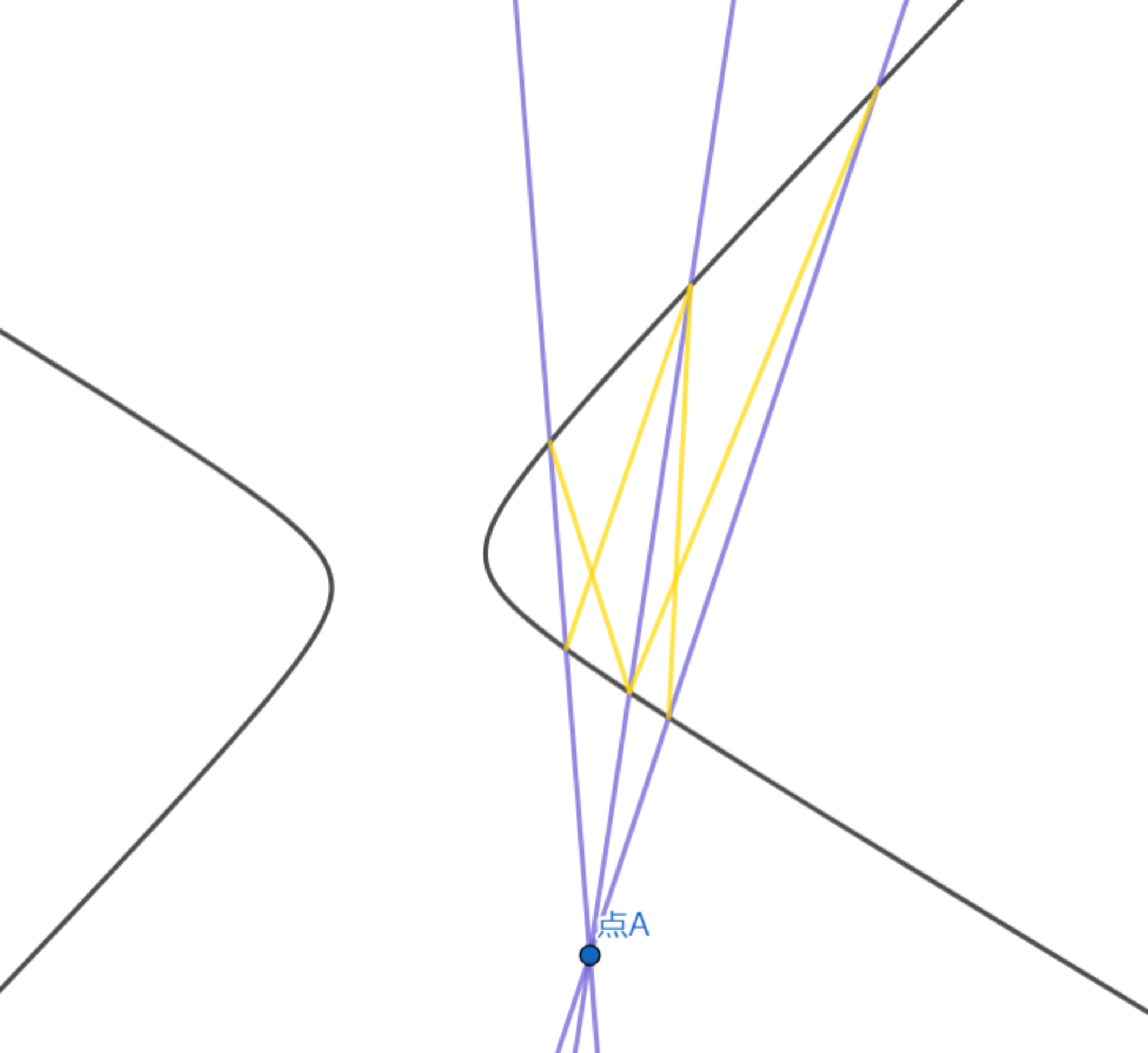
方法2-手順1 直線を2本引き、双曲線との交点をつなぐ直線を４本引く

直線を２本引き、双曲線との交点をつなぐ直線を４本引く

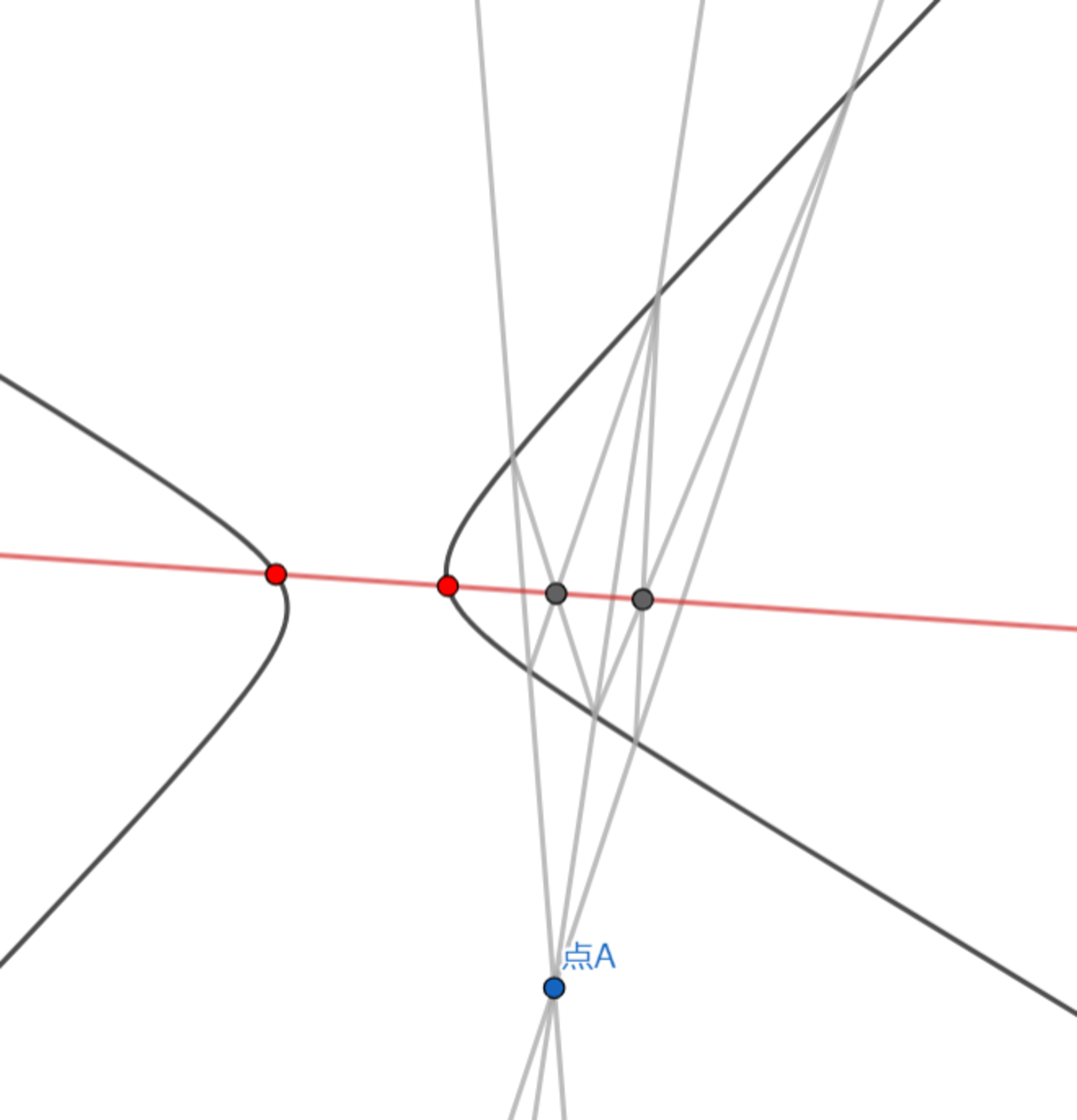
方法2-手順2　新たな交点をつなぐ直線を引き、双曲線との交点を作図する

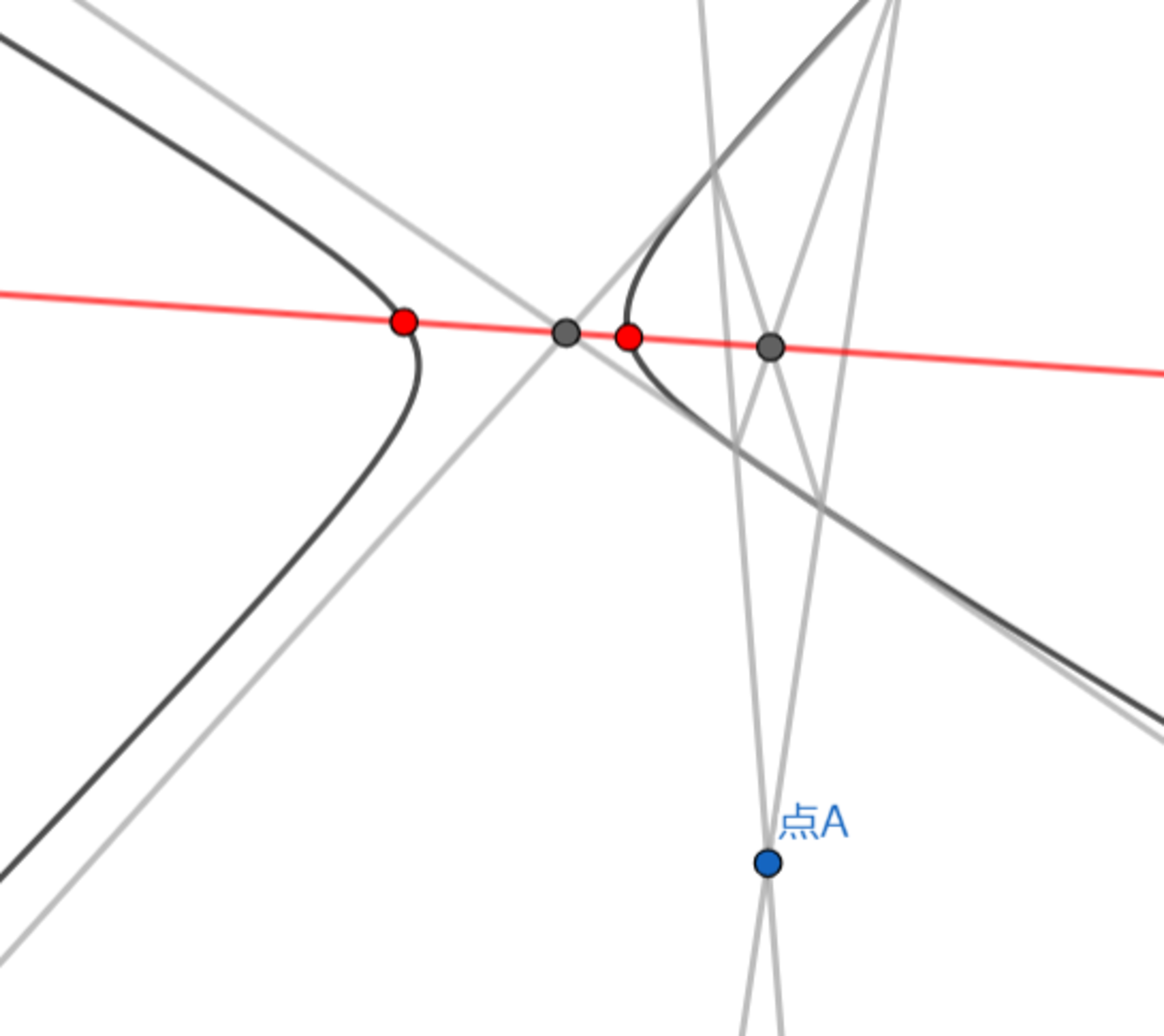新たな交点をつなぐ直線を引き、双曲線との交点を作図する

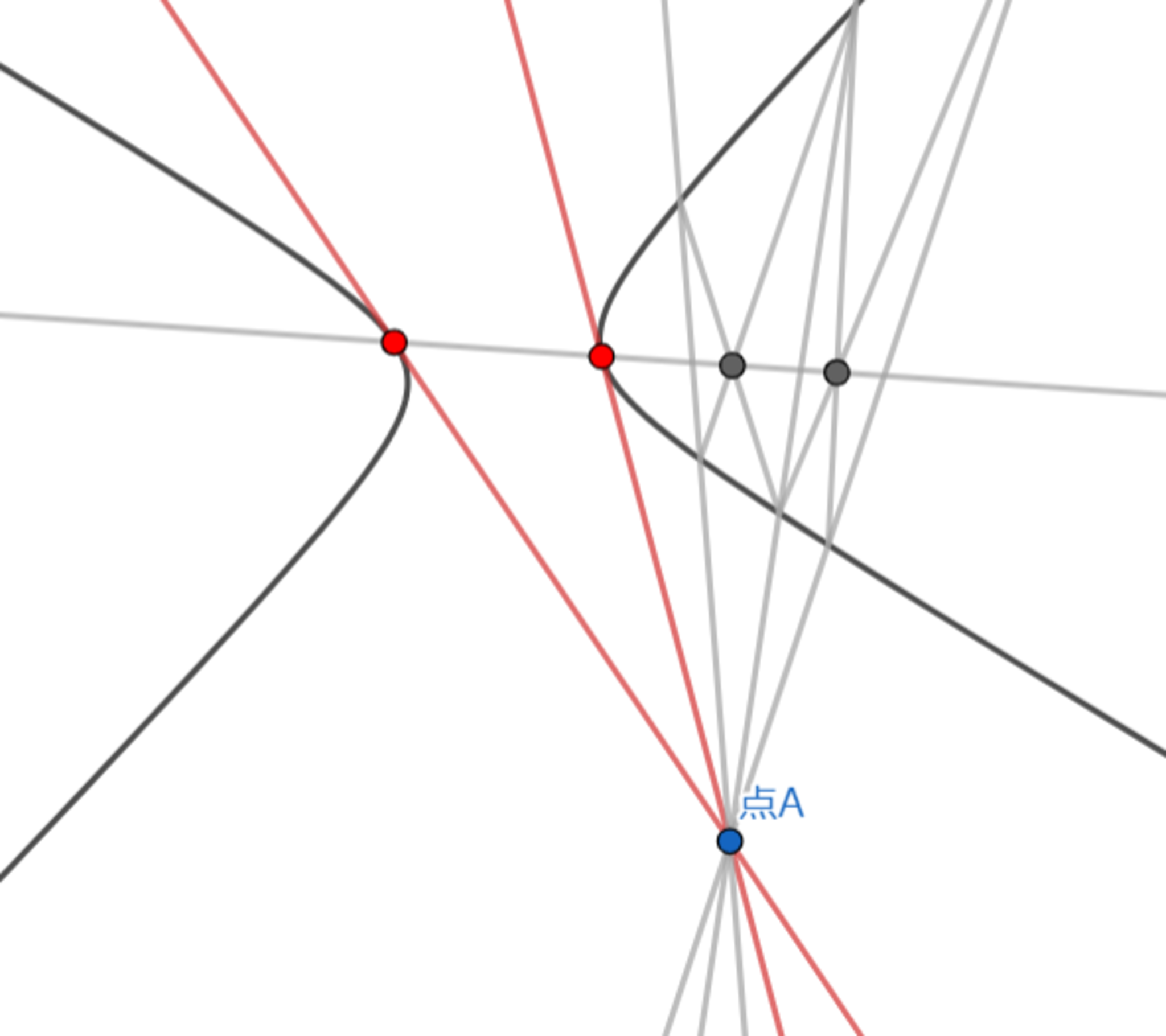
方法2-手順3　双曲線の接線を引く

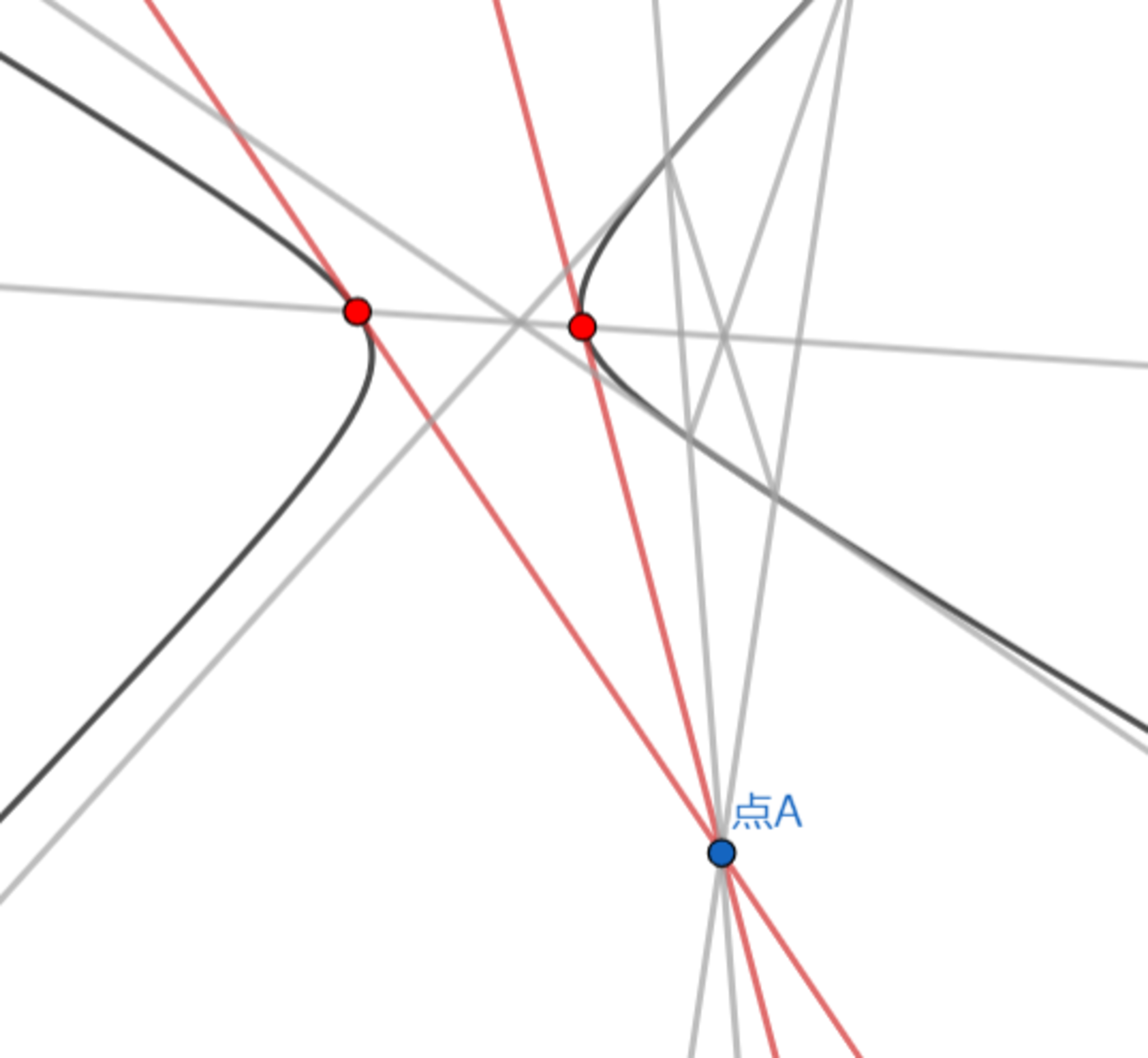双曲線の接線を引く

これで完成です!

この方法でうまくいくわけ

この方法で得られる、双曲線との接点をつなぐ直線は極線 (Polar) と呼ばれており、この場合の点$A$は極　(Pole)　と呼ばれています。

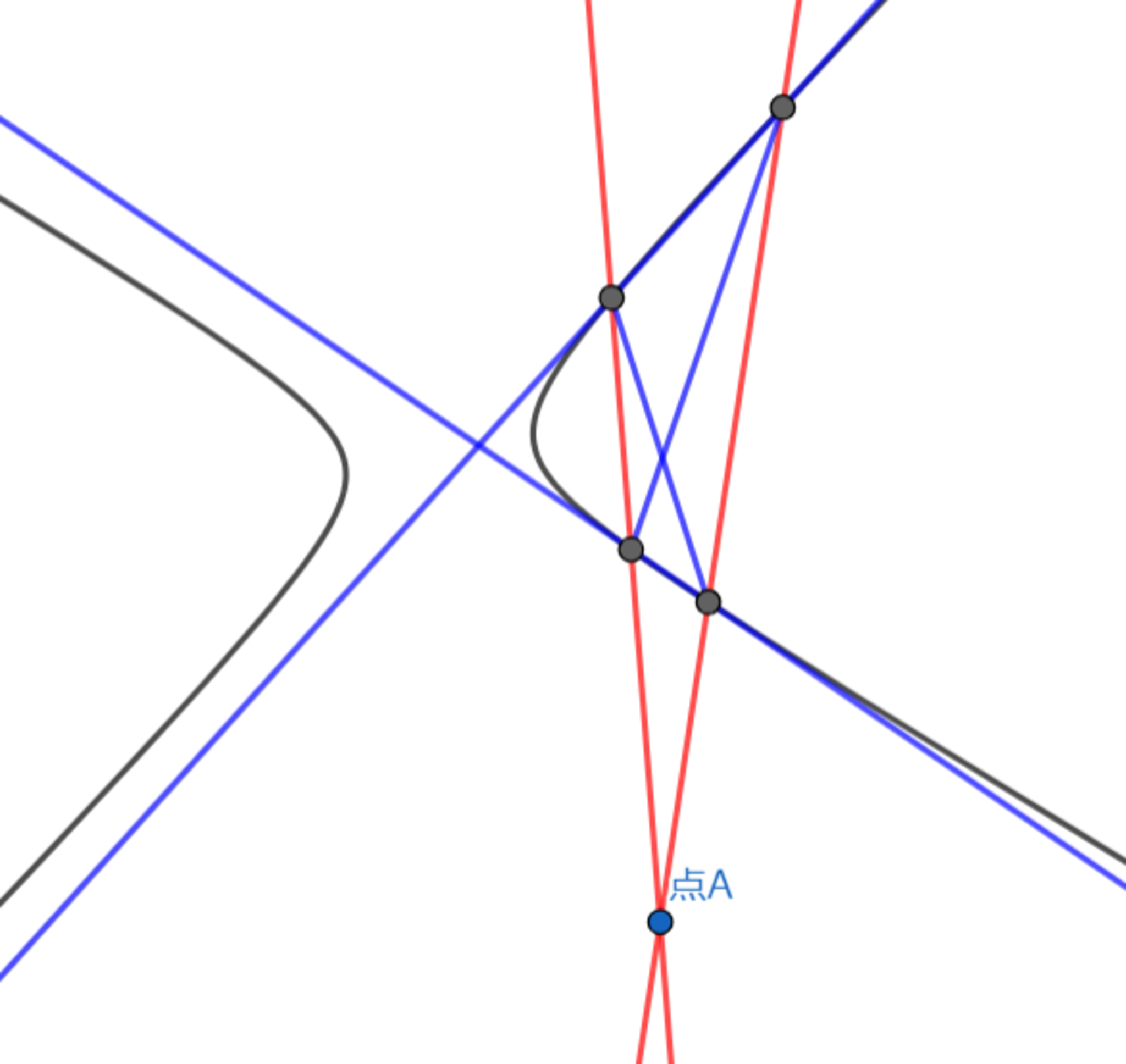
まず、上記方法2-手順1で得られる4点と6本の直線からなる形を完全四角形 (complete quadrangle) と解釈します。
完全四角形とは、「射影平面上のどの3点も一直線上にない4点と，それらの2点を通る6直線からなる図形」をいいます(下図参照)。完全四角形の各頂点を結ぶ線は3つの対角点で交差します。

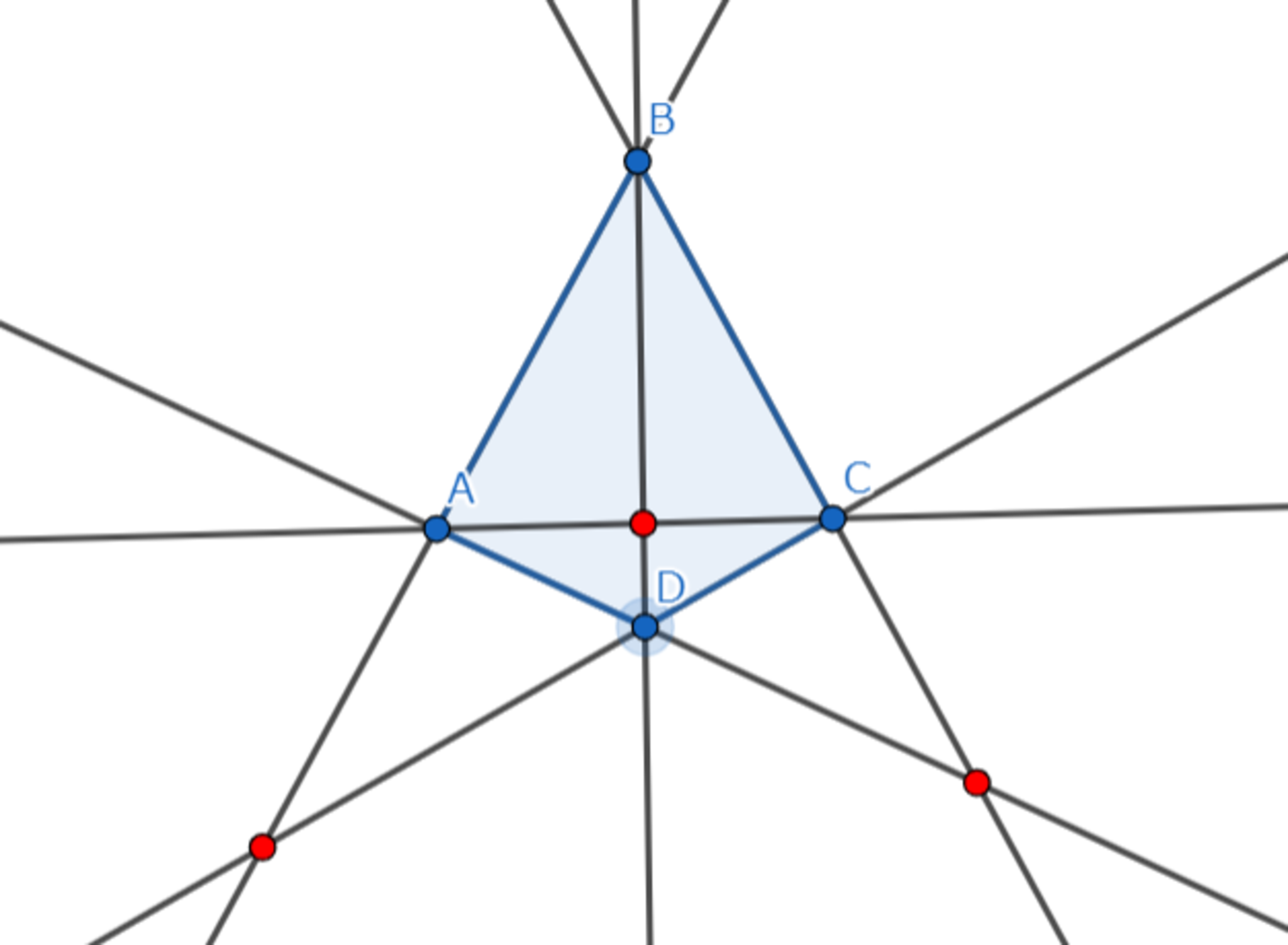完全四角形と3つの対角点の例1
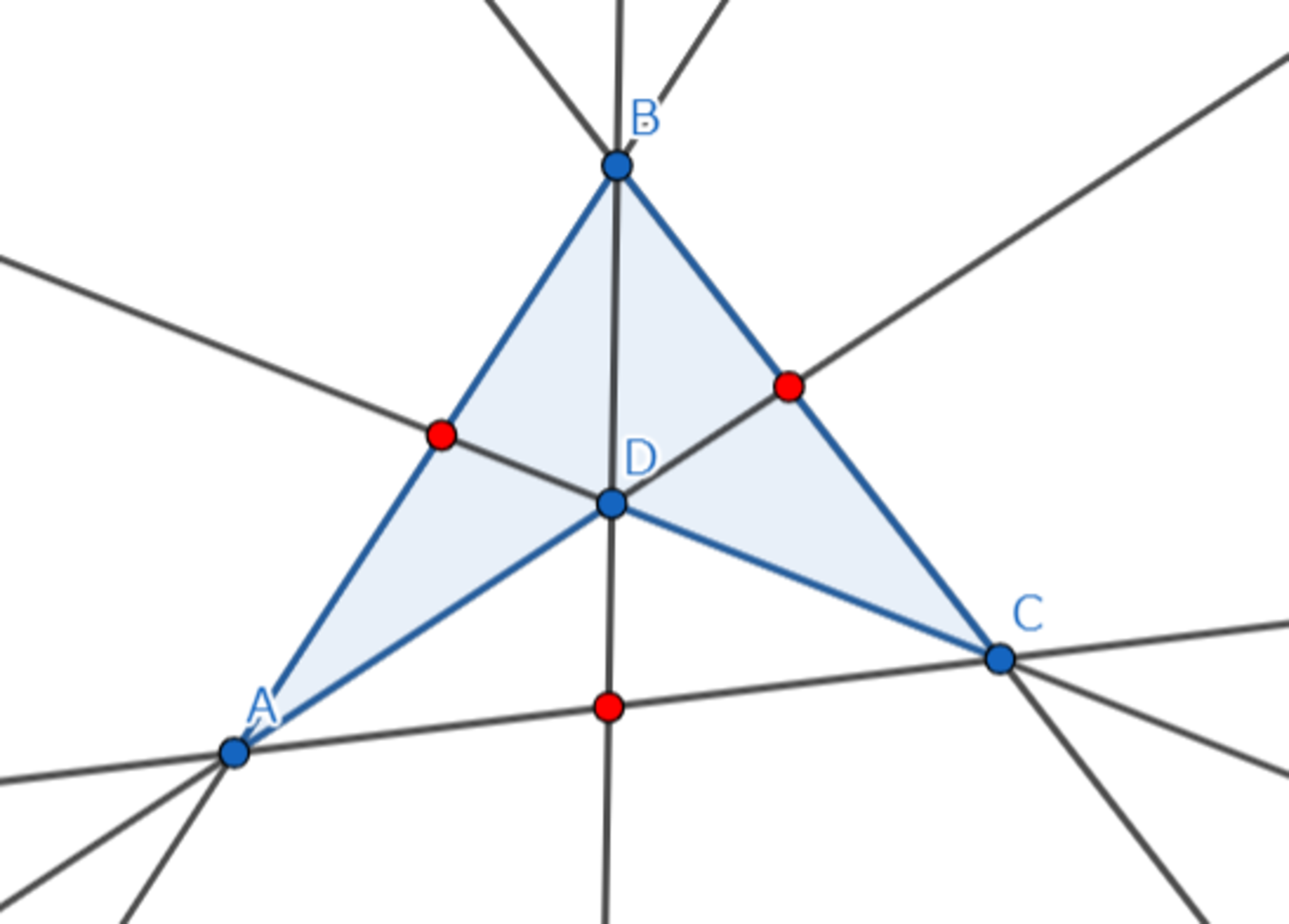完全四角形と3つの対角点の例2

円錐曲線$C$上にない点$Z$があるとき、$Z$から$C$と4点で交差する2本の割線(secant)を引くと、これらの4点は$Z$を対角点の1つとする完全四角形を形成します。他の2つの対角点を結ぶ線は$Z$を極としたときの極線となることから知られています。

参考： Wikipedia(en)Pole_and_polar#Via_complete_quadrangle

参考： G. B. Halsted (1906) Synthetic Projective Geometry, page 25 via Internet Archive

(この情報は @erugli さんに Twitter で教えていただきました。ありがとうございます。)

上記の「方法2」はこの性質を直接使った方法で、「方法1」はそれを応用した方法になっていることがおわかりいただけますでしょうか。
それでは、次に漸近線の作図方法を説明します。

定規とコンパスだけで双曲線の漸近線を作図する方法

前提

平面上に双曲線があります。この双曲線の漸近線を作図したいと思います。

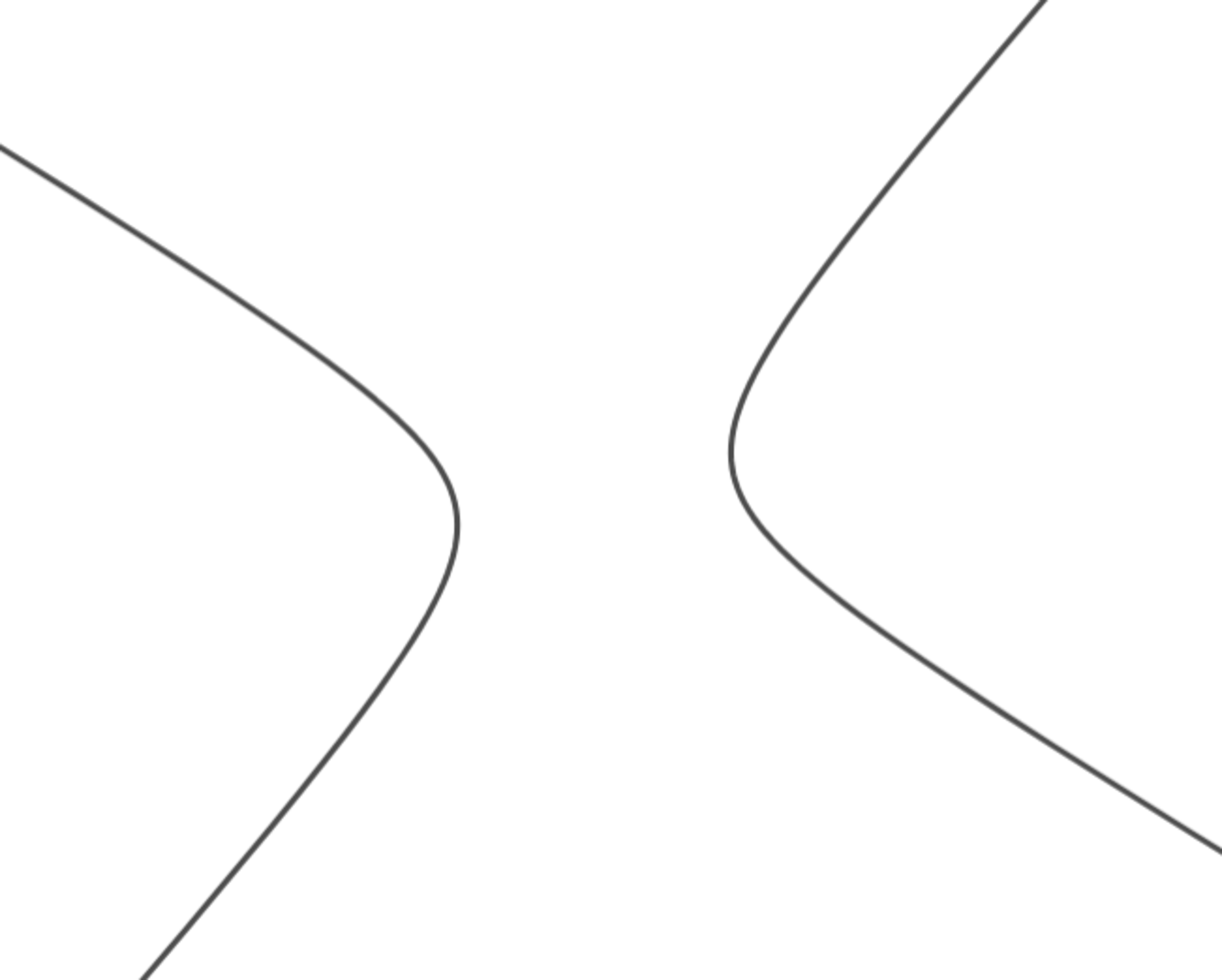双曲線

手順1 平行線を3本引き、交点を結ぶ

三本の平行線を引き、交点をつなぐ直線を引く

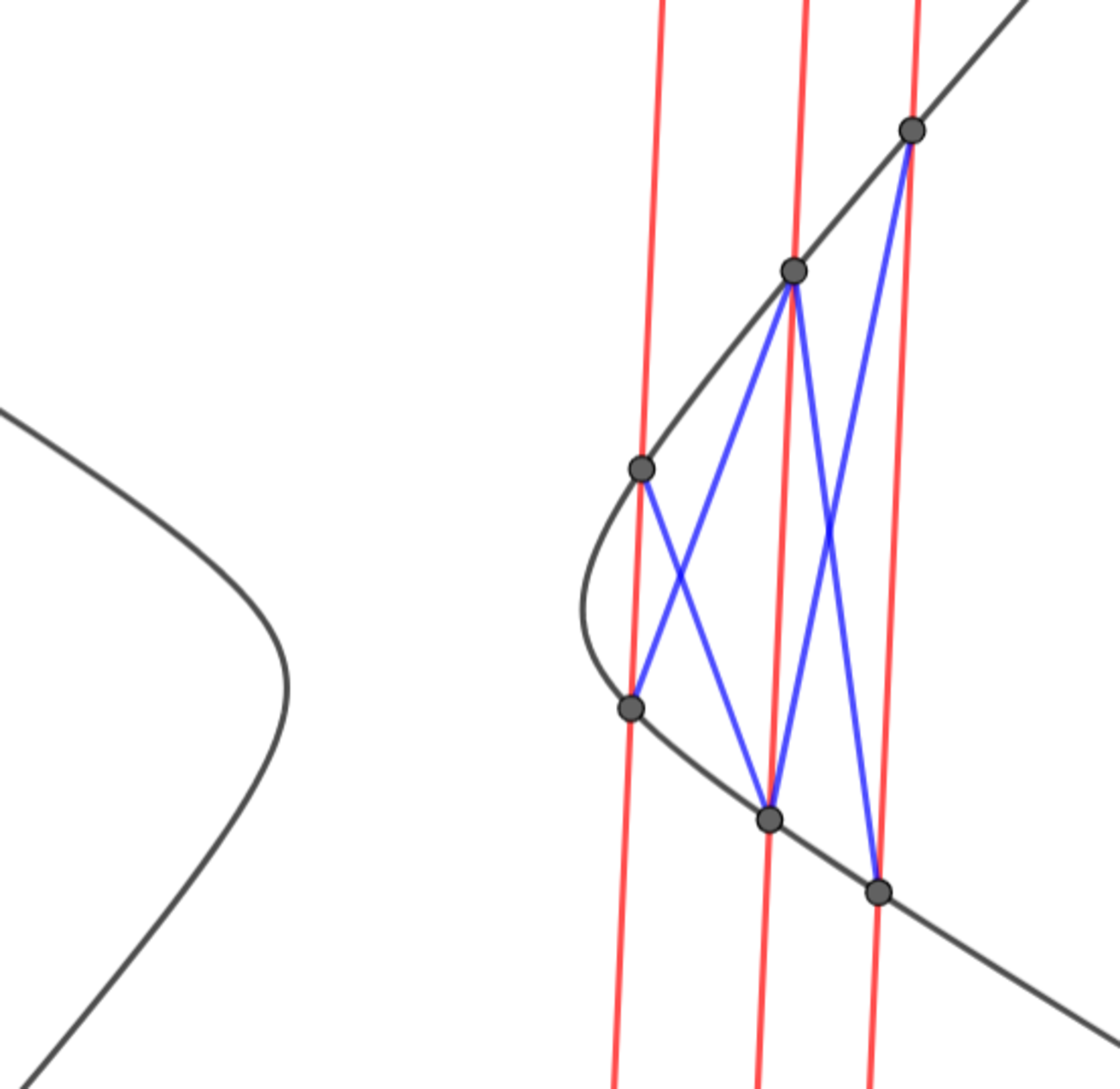
手順2 新たな交点をつなぐ直線を引き、双曲線との交点を作図する

新たな交点をつなぐ直線を引き、双曲線との交点を作図する

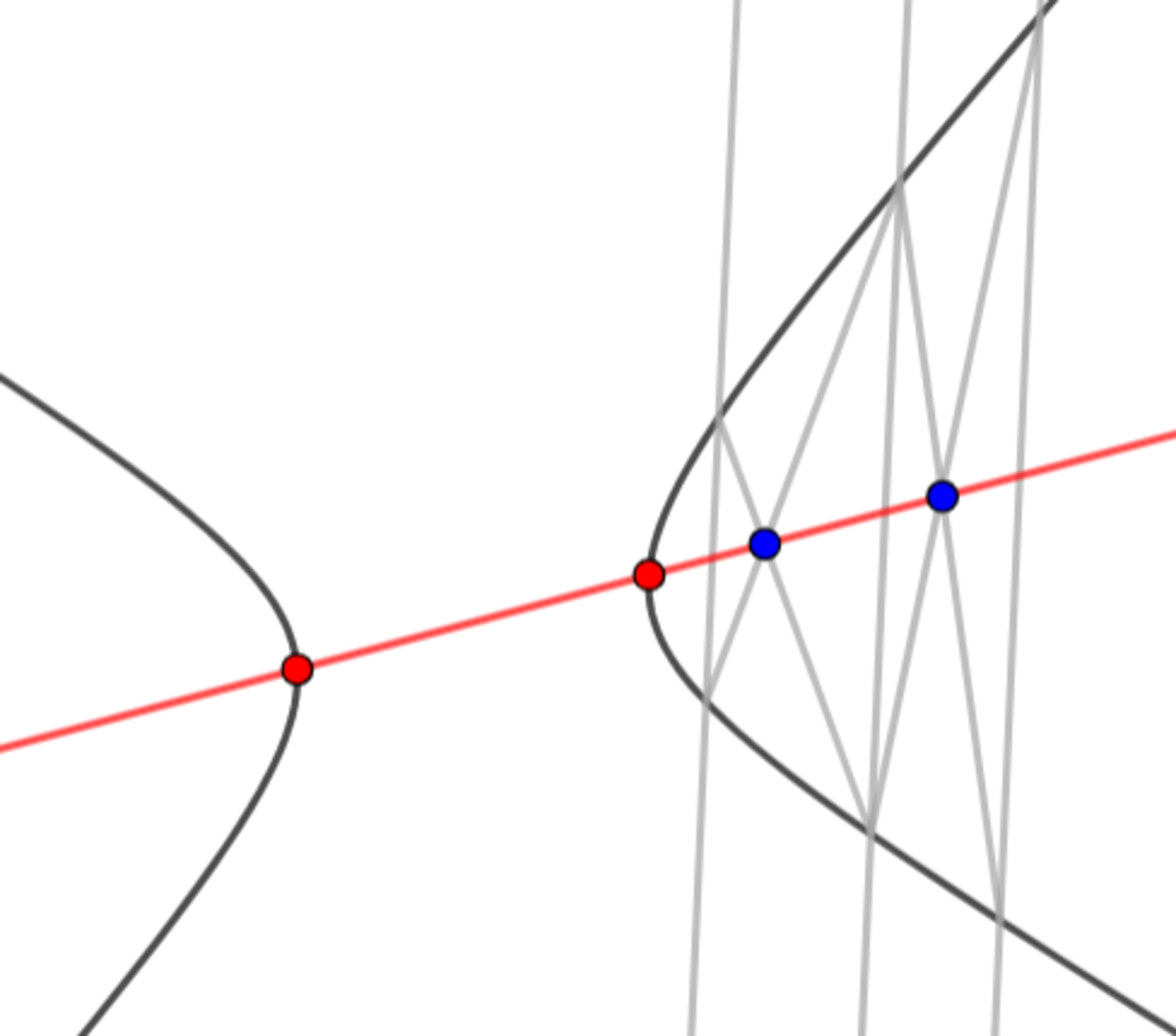
手順3 中点をとり、双曲線の中心を作図する

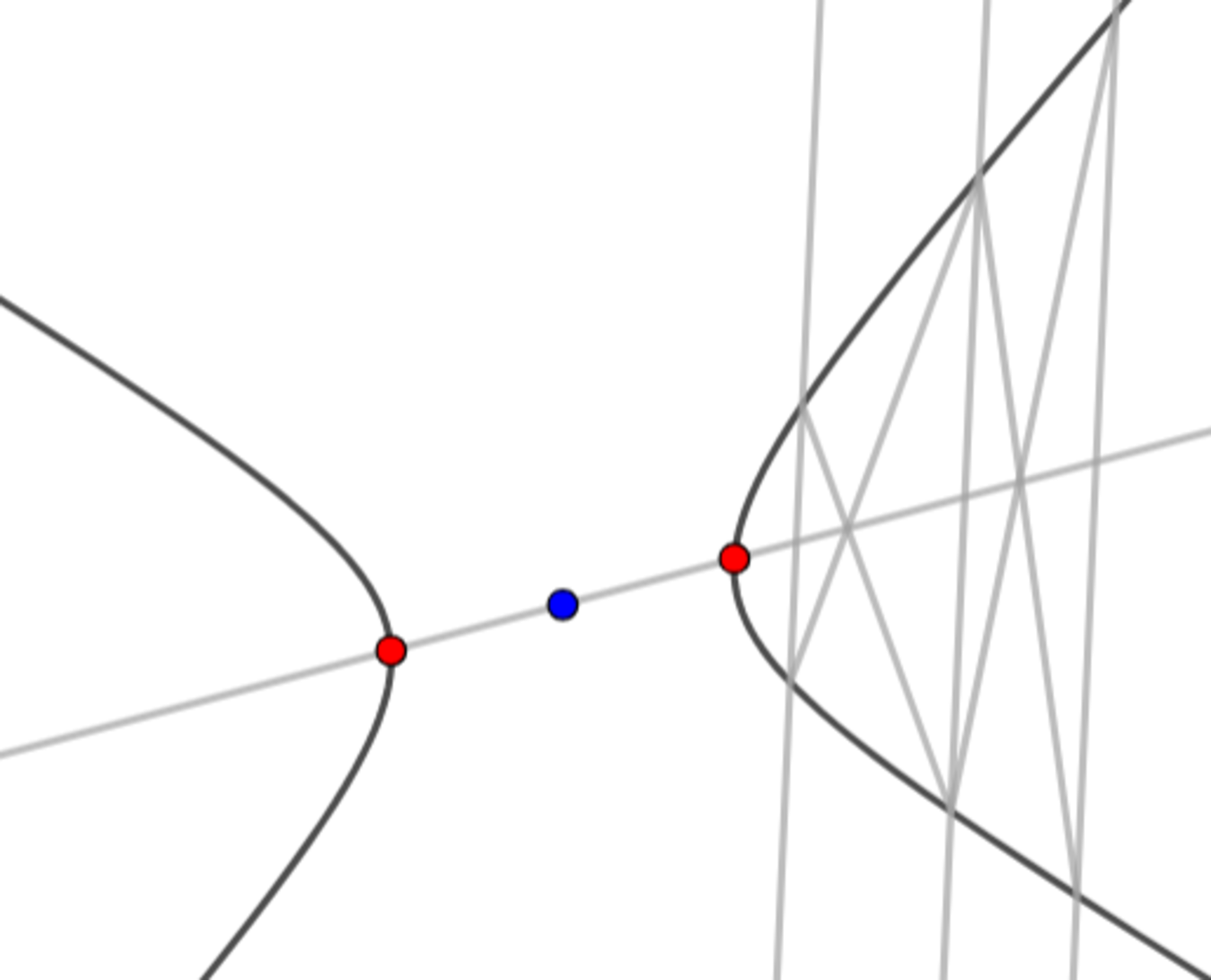中点をとり、双曲線の中心を作図する

手順4 双曲線の中心に中心があり、双曲線に接する円を作図する

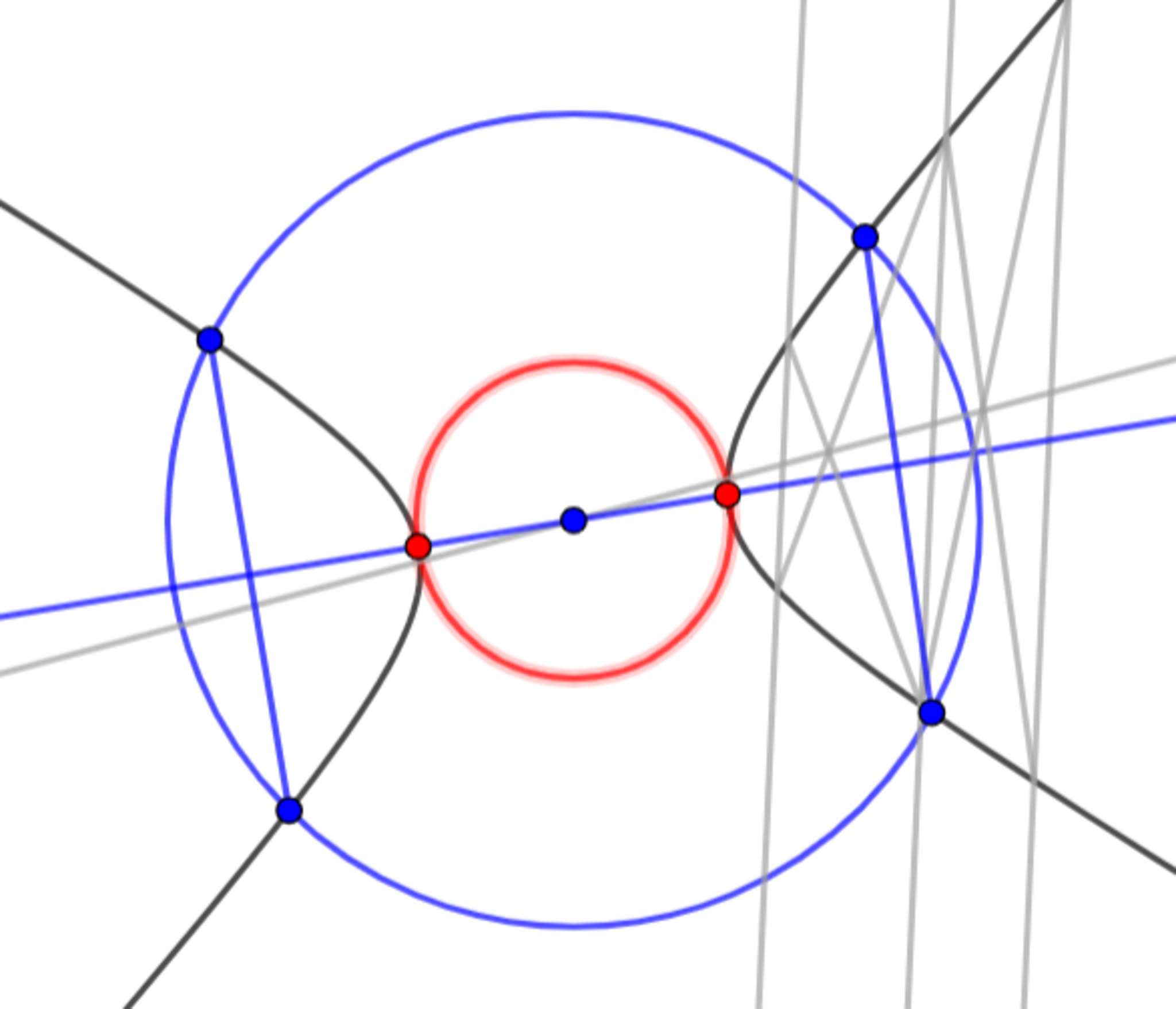双曲線の中心に中心があり、双曲線に接する円を作図する

手順5 円に接する平行線と双曲線の交点を作図する

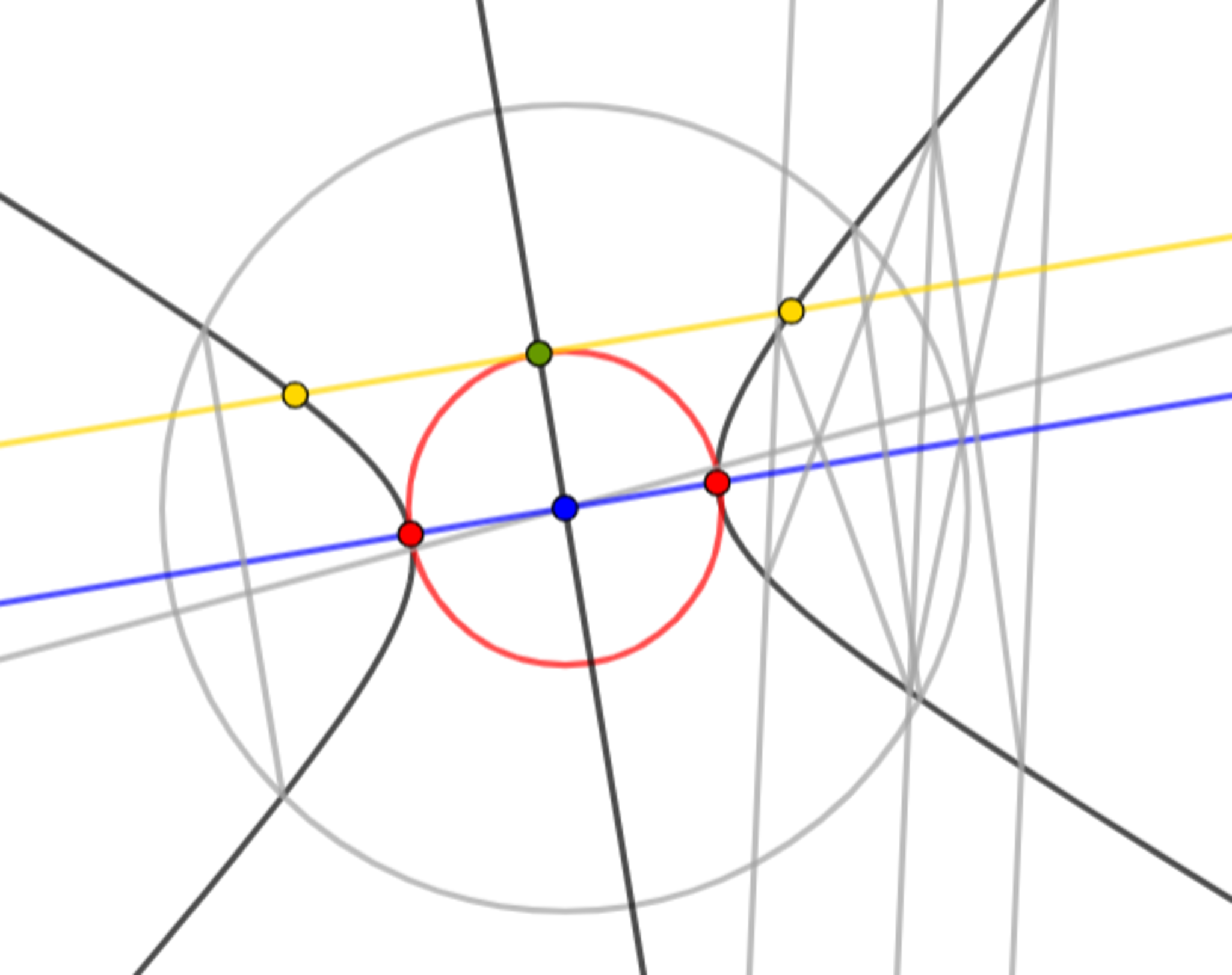円に接する平行線と双曲線の交点を作図する

手順6 双曲線との交点間の距離を直径とする円を作図する

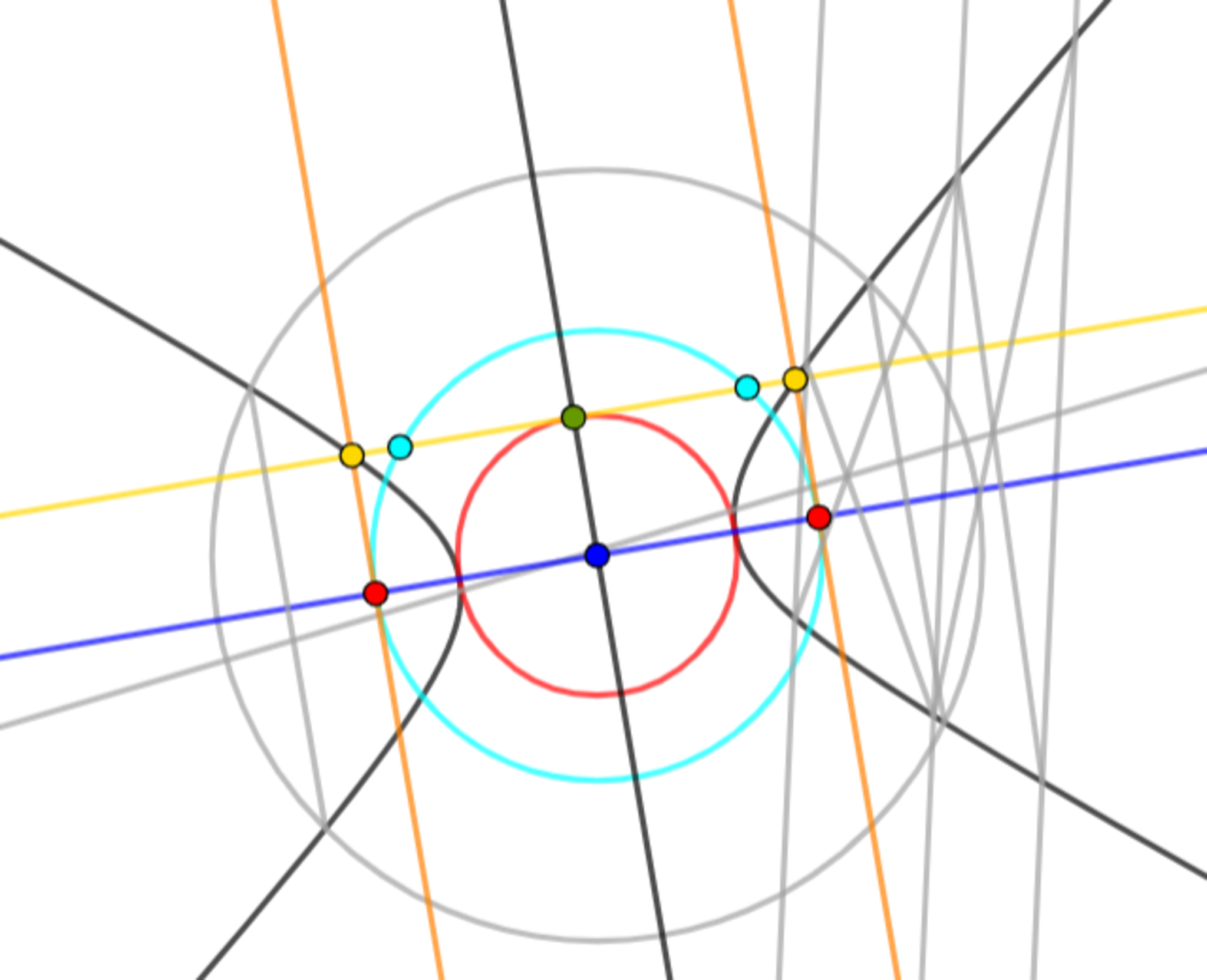双曲線との交点間の距離を直径とする円を作図する

手順7　双曲線の漸近線を引く

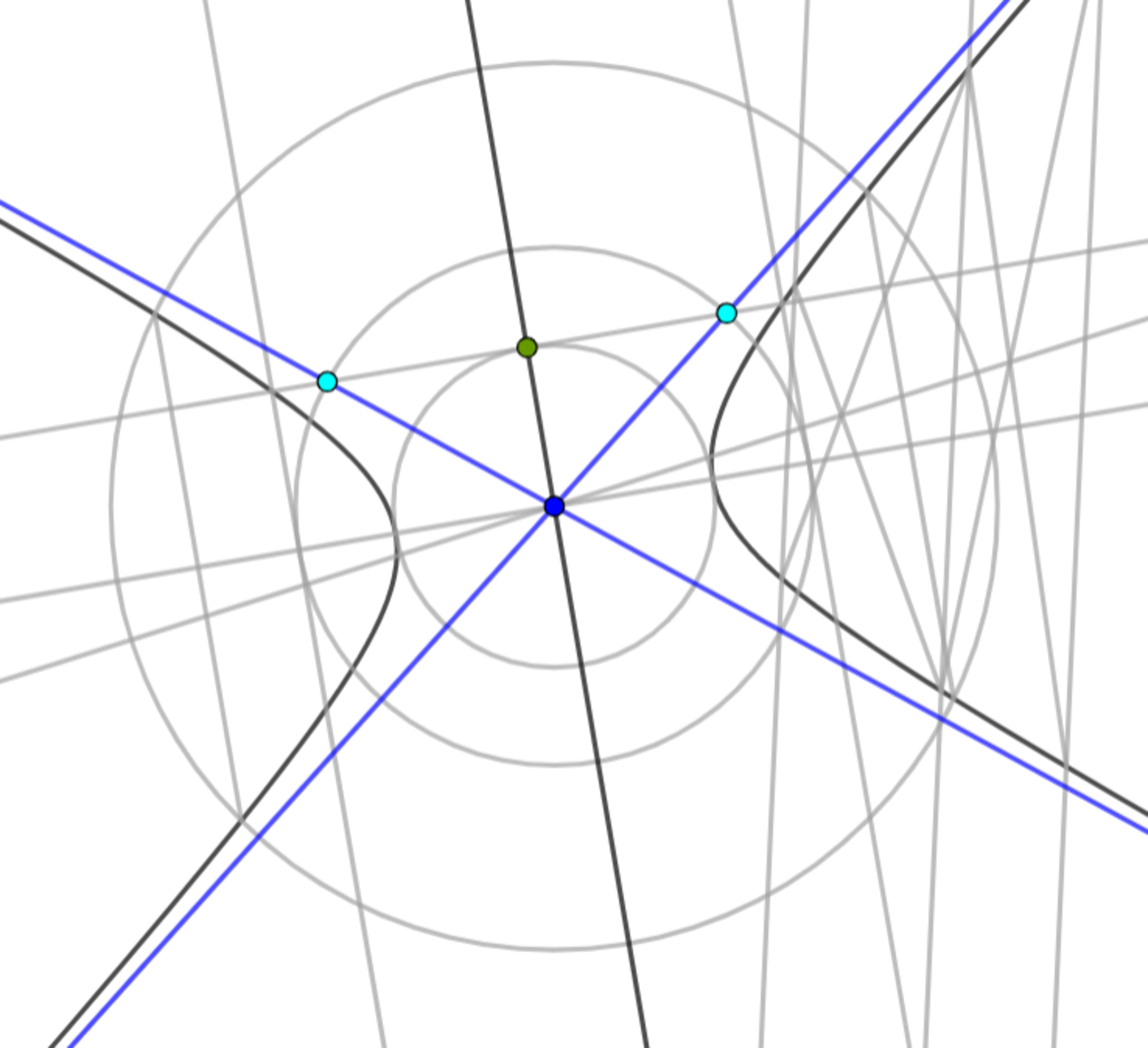双曲線の漸近線を引く

これで完成です!

漸近線が引ける理由

なぜこの方法で漸近線がひけるのでしょうか?
それを説明します。
まずはこの図を見てください。

双曲線に無数の接線を引く

これは双曲線に無数の接線を引いたものです。なんだか立体的に見えませんか?
実際、このグラフは立体グラフとして解釈することができます!
立体グラフと解釈したうえで、少し斜めにしてみましょう。

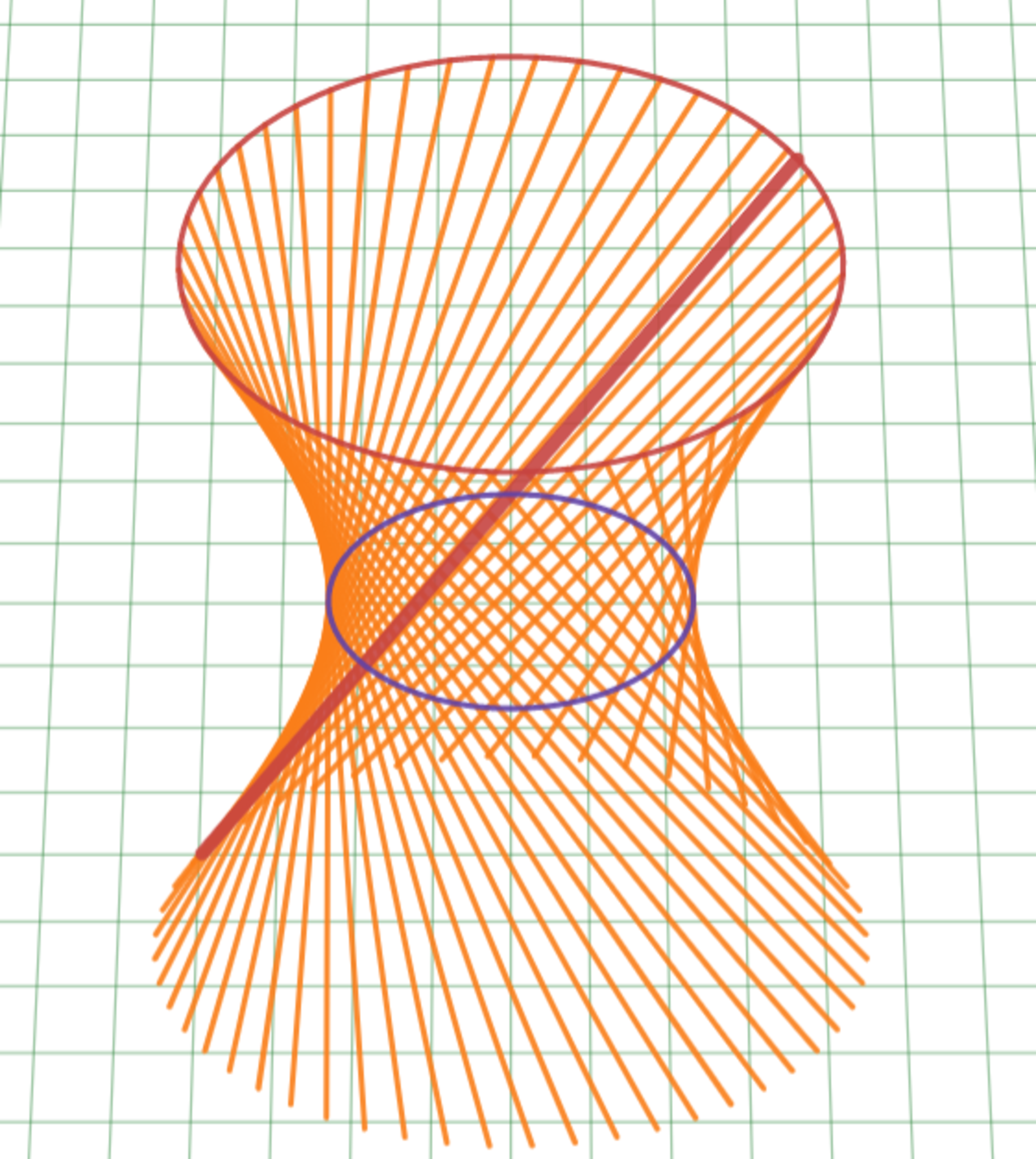無数の接線のグラフを立体グラフとして解釈する

さらに角度をつけて、今度は真上から見てみましょう。

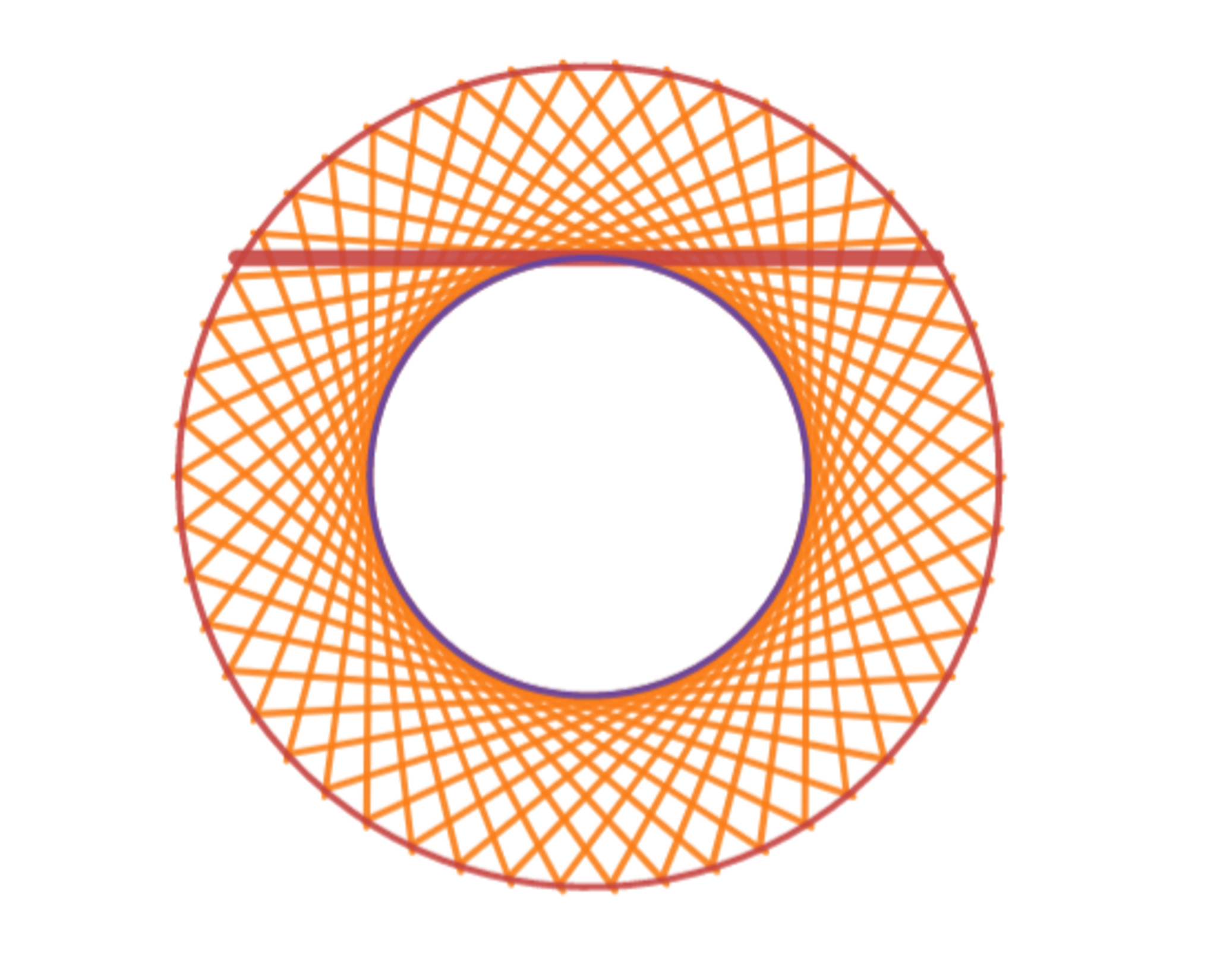立体グラフを真上から見る

Desmosへのリンク

双曲線の接線たちは、真上から見ると小円の接線になったことがわかりますね。
特に、赤い直線は接点が無限遠にある接線、すなわち漸近線を表す線ですが、真上から見ると小円の接線となっていますね!
先ほどの方法は、このことを利用して漸近線が通る点を作図したものでした。