卵2個で落としたら割れる階数を調べる問題とメルカトル級数
はじめに
最近Twitterで話題になっている、ビルの何階から落とすと卵が割れるかを卵を2つだけ使って調べる回数の問題について考えていたところ、メルカトル級数の式があらわれてビックリしたのでこの記事を書きました。
問題の確認
この問題は、かつてGoogleの入社試験で出たといわれている問題です。
なるべく正確に問題の内容を確認します。
100階建てのビルから卵を落としたとして、どの階までなら割れないか、そしてどの階からだと割れるか、知りたいとします。その階を見つけるには、そしてその階を決めるためにかかる最大の回数を一番小さくするにはどうしたらいいでしょうか。
次の仮定が成り立つとします。
・落として割れなかった卵はもう一度使えます
・割れた卵は二度と使えません
・落下時の衝撃はどちらの卵でも変わりません
・落とした卵が割れたら、それより上の階から落としても割れます
・落とした卵が割れなかったら、それより下の階から落としても大丈夫
・引用元
卵2個で、落としたら割れる階を特定する
Puzzle | Set 35 (2 Eggs and 100 Floors)
メルカトル級数の確認
メルカトル級数とは、$\log 2$ が出てくる次のような無限級数です。
$ 1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6} \pm\cdots=\log2 $
問題の一般化
ここでは、あえて問題を次のように一般化します。
$n$ 個の卵を使って、最大 $k$ 回の試行で、ビルの何階までなら割れないか、そしてどの階からだと割れるかを調べられる最大のビルの階数を $a_{n,k}$ とします。 $a_{n,k}$ を$n,k$の式で表してください。
次の仮定が成り立つとします。
・落として割れなかった卵はもう一度使えます
・割れた卵は二度と使えません
・落下時の衝撃はどちらの卵でも変わりません
・落とした卵が割れたら、それより上の階から落としても割れます
・落とした卵が割れなかったら、それより下の階から落としても大丈夫
漸化式を作る
割れなかった卵は再利用できますので、1階から順に調べれば確実に割れる階を調べられます。
すなわち、卵を1個使って、$k$ 回の試行をすれば、$k$ 階までを調べることができます。
式にすると
$a_{1,k}=k$
また、卵が何個あったとしても、1回の試行では1階しか調べることはできません。
式にすると
$a_{n,1}=1$
次に、漸化式を考えます。
たとえば、50階建てのビルを5個の卵を使って調べるとして、最初の1個目を20階から落としたとします。
もし、20階から落とした卵が割れなかったら、次に21~50階を5個の卵で調べることになります。卵が割れたら、次に1~19階を4個の卵で調べることになります。
これを一般的化して調べられる最大の階数を考えれば、次の漸化式が得られます。
$a_{n,k}=a_{n,k-1}+1+a_{n-1,k-1}$
$\begin{cases} a_{1,k}=k\\ a_{n,1}=1\\ a_{n,k}=a_{n,k-1}+1+a_{n-1,k-1} \end{cases}$
さて、漸化式を繰り返し使って、$a_{n,*}$ を $a_{n-1,*}$ で表すことを考えます。
${\displaystyle \begin{align} a_{n,k}&=a_{n,k-1}+1+a_{n-1,k-1}\\ &=\left(a_{n,k-2}+1+a_{n-1,k-2}\right)+1+a_{n-1,k-1}\\ &=a_{n,k-2}+2+(a_{n-1,k-2}+a_{n-1,k-1})\\ &=a_{n,k-3}+3+(a_{n-1,k-3}+a_{n-1,k-2}+a_{n-1,k-1})\\ &=a_{n,k-4}+4+(a_{n-1,k-4}+a_{n-1,k-3}+a_{n-1,k-2}+a_{n-1,k-1})\\ &\qquad\vdots\\ &=a_{n,1}+(k-1)+\sum_{j=1}^{k-1}a_{n-1,j}\\ &=k+\sum_{j=1}^{k-1}a_{n-1,j}\\ &=1+\sum_{j=1}^{k-1}(a_{n-1,j}+1)\\ \end{align} }$
${\displaystyle
\therefore(a_{n,k}+1)=2+\sum_{j=1}^{k-1}(a_{n-1,j}+1)\\
}$
式を見やすくするため、次のような $b_{n,k}$ を導入します。
$b_{n,k}=a_{n,k}+1$
$b_{n,k}$ を使ってこれまでの式を書き直すとこうなります。
${\displaystyle \begin{cases} b_{1,k}=1+k\\ b_{n,k}=2+\sum_{j=1}^{k-1}(b_{n-1,j}) \end{cases} }$
なかなかいい感じになってきましたね。さらに漸化式部分を計算するために、下降階乗冪と和分を使います。
下降階乗冪と和分
下降階乗冪とは次のような演算です。
${\displaystyle t^{\underline{m}}=t(t-1)(t-2)\cdots(t-m+1) }$
たとえば
${\displaystyle
5^{\underline{3}}=5\cdot4\cdot3=60
}$
となります。
下降階乗冪を使うと、「積分」の離散バージョンの「和分」として、次の式が成り立ちます。
${\displaystyle \sum_{t=0}^{n-1} t^{\underline{m}}= \frac{n^{\underline{m+1}}}{m+1} \qquad ( m\ge 0) }$
式の形から、これは積分の
${\displaystyle
\int_{0}^n x^{m}\,dx=
\frac{n^{m+1}}{m+1}
}$
の離散バージョンと解釈できます。
和分を使って閉じた式にする
さて、和分の公式を使えば $b_{n,k}$ を閉じた式にできます。
${\displaystyle \begin{align} b_{1,k}&=1+k\\ b_{2,k}&=2+\sum_{j=1}^{k-1}(1+j)\\ &=1+\sum_{j=0}^{k-1}(1+j)\\ &=1+\frac{k^{\underline{1}}}{1!}+\frac{k^{\underline{2}}}{2!}\\ b_{3,k}&=2+\sum_{j=1}^{k-1}\left( 1+\frac{j^{\underline{1}}}{1!}+\frac{j^{\underline{2}}}{2!} \right)\\ &=1+\sum_{j=0}^{k-1}\left( 1+\frac{j^{\underline{1}}}{1!}+\frac{j^{\underline{2}}}{2!} \right)\\ &=1+\frac{k^{\underline{1}}}{1!}+\frac{k^{\underline{2}}}{2!}+\frac{k^{\underline{3}}}{3!}\\ \end{align} }$
以下同様に繰り返すことで次の式を得ます。
${\displaystyle \begin{align} b_{n,k} &=1+\frac{k^{\underline{1}}}{1!}+\frac{k^{\underline{2}}}{2!}+\frac{k^{\underline{3}}}{3!}+\cdots+\frac{k^{\underline{n}}}{n!}\\ &=\sum_{j=0}^{n} \frac{k^{\underline{j}}}{j!} \end{align} }$
一般化した問題の答え
$a_{n,k}=b_{n,k}-1$
なので一般化した問題の答えは次のようになります。
${\displaystyle \begin{align} a_{n,k} &=\sum_{j=1}^{n} \frac{k^{\underline{j}}}{j!} \end{align} }$
とてもシンプルな式になりましたね!
具体例
得られた式をもと表を作るとこんな感じになります。
| k \ n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| 3 | 3 | 6 | 7 | 7 | 7 | 7 | 7 | 7 |
| 4 | 4 | 10 | 14 | 15 | 15 | 15 | 15 | 15 |
| 5 | 5 | 15 | 25 | 30 | 31 | 31 | 31 | 31 |
| 6 | 6 | 21 | 41 | 56 | 62 | 63 | 63 | 63 |
| 7 | 7 | 28 | 63 | 98 | 119 | 126 | 127 | 127 |
| 8 | 8 | 36 | 92 | 162 | 218 | 246 | 254 | 255 |
| 9 | 9 | 45 | 129 | 255 | 381 | 465 | 501 | 510 |
| 10 | 10 | 55 | 175 | 385 | 637 | 847 | 967 | 1012 |
| 11 | 11 | 66 | 231 | 561 | 1023 | 1485 | 1815 | 1980 |
| 12 | 12 | 78 | 298 | 793 | 1585 | 2509 | 3301 | 3796 |
| 13 | 13 | 91 | 377 | 1092 | 2379 | 4095 | 5811 | 7098 |
| 14 | 14 | 105 | 469 | 1470 | 3472 | 6475 | 9907 | 12910 |
| 15 | 15 | 120 | 575 | 1940 | 4943 | 9948 | 16383 | 22818 |
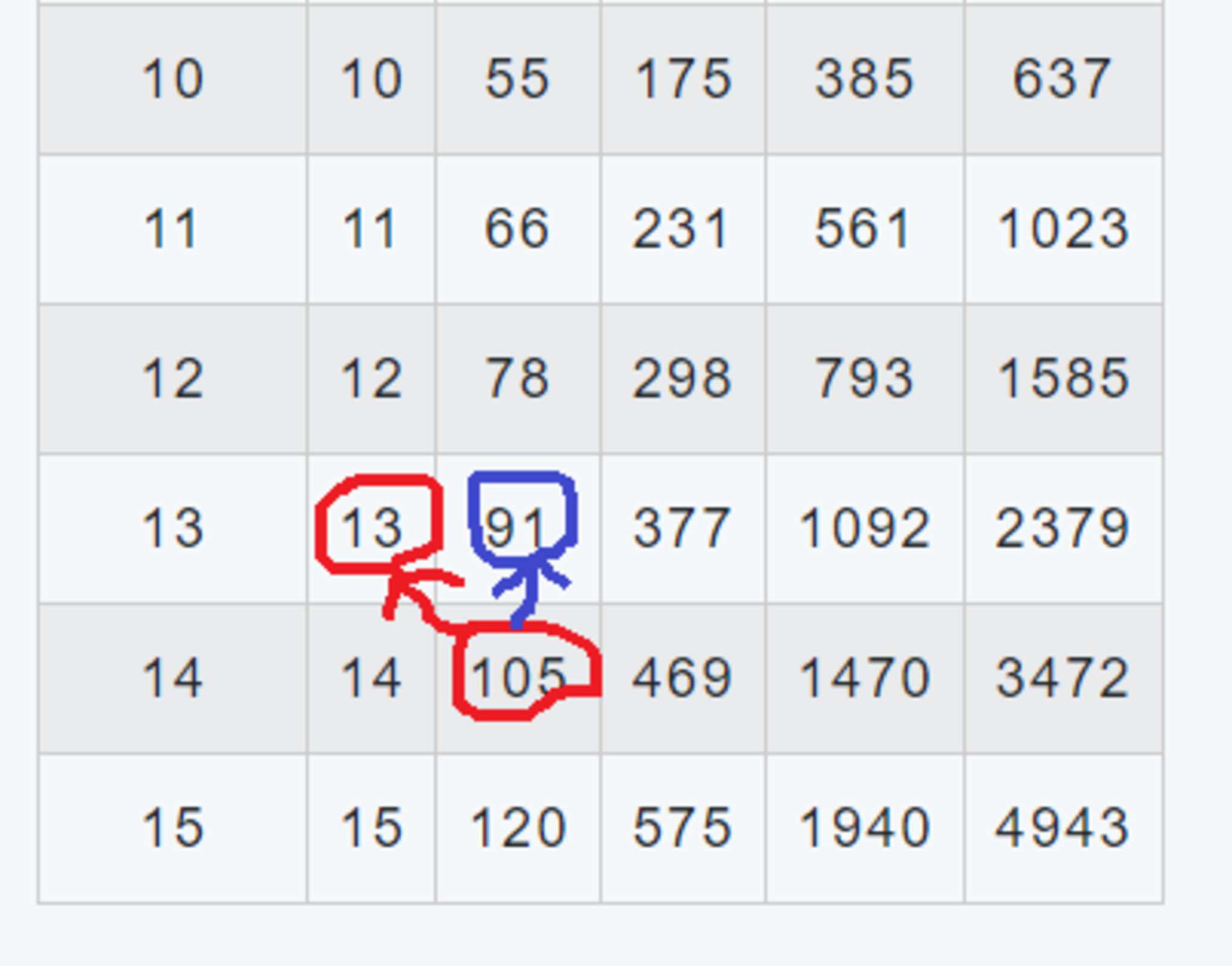
例えば、「卵2個13回の試行」で調べられる最大の階数は91階で、「卵2個14回の試行」で調べられる最大の階数は105階ですから、冒頭のGoogleの入社試験の問題での試行回数は最大14回ということになります。
105階のビルで試行する場合で考えると、最初の1回は14階から落とし、
①割れた場合は1~13階を「13階建てのビル」とみなして1個の卵で引き続き調べ、
②割れなかった場合は15~105階を「91階建のビル」とみなして2個の卵で引き続き調べればよい
ということも表から読み取ることができます。
表でいうと、「卵が割れたら左上へ1つ移動し、割れなかったら上へ1つ移動する」という操作が試行に対応していることになります。
 具体例
具体例
離散バージョンのマクローリン展開
ところで、先ほどの
${\displaystyle
\begin{align}
b_{n,k}
&=1+\frac{k^{\underline{1}}}{1!}+\frac{k^{\underline{2}}}{2!}+\frac{k^{\underline{3}}}{3!}+\cdots+\frac{k^{\underline{n}}}{n!}\\
\end{align}
}$
は離散バージョンの $2^k$ のマクローリン展開(の途中項まで)と解釈することができます。
つまり
${\displaystyle
\begin{align}
2^k
&=1+\frac{k^{\underline{1}}}{1!}+\frac{k^{\underline{2}}}{2!}+\frac{k^{\underline{3}}}{3!}+\cdots\\
&=1+\frac{k}{1!}+\frac{k(k-1)}{2!}+\frac{k(k-1)(k-2)}{3!}+\cdots\\
\end{align}
}$
という式が成り立っています。
メルカトル級数との関係
一方で、$2^k$ を普通にマクローリン展開するとこうなります。
${\displaystyle
2^k=1+\frac{\log(2)k}{1!}+\frac{\log^2(2)k^2}{2!}+\frac{\log^3(2)k^3}{3!}+\cdots
}$
離散バージョンと普通バージョンの1次の項の係数を比較すると
${\displaystyle \begin{align} \frac{\log(2)}{1!}&=\frac{1}{1!}+\frac{-1}{2!}+\frac{(-1)(-2)}{3!}+\frac{(-1)(-2)(-3)}{4!}+\cdots\\ &=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}\pm\cdots \end{align} }$
となって、メルカトル級数の式が現れました!
卵の問題からメルカトル級数の式が出てくるとは、ビックリだと思いませんか?
