連続化したフィボナッチ数を三項間漸化式で定義する
はじめに
この記事ではフィボナッチ数を $\{F_{[1],n}\}$ で表します。
${\displaystyle \{F_{[1],n}\}=\{0,1,1,2,3,5,8,13,21,34,55,89,144,\cdots\}\qquad(n=0,1,2,3,\cdots)}$
リュカ数を $\{L_{n}\}$ で表します。
${\displaystyle \{L_{n}\}=\{2,1,3,4,7,11,18,29,47,76,123,199,\cdots\}\qquad(n=0,1,2,3,\cdots)}$
黄金比 $\varphi$ を次のように定義します。
${\displaystyle \varphi=\frac{1+\sqrt{5}}{2}}$
フィボナッチ数の「自然数の倍数項」からなる数列の三項間漸化式による定義
$2$の倍数項の場合
$\{F_{[1],n}\}$ の2の倍数項からなる数列、つまり次の下線部からなる数列 $\{F_{[2],n}\}$ を考えます。
$\underline{0},1,\underline{1},2,\underline{3},5,\underline{8},13,\underline{21},34,\underline{55},89,\underline{144},\cdots$
${\displaystyle \{F_{[2],n}\}=\{0,1,3,8,21,55,144,\cdots\}\qquad(n=0,1,2,3,\cdots)}$
この数列は、次のように三項間漸化式で定義することができます。
$$ \begin{eqnarray} \left\{ \begin{array}{l} F_{[2],0}=0 \\ F_{[2],1}=1 \\ F_{[2],n+2}=3F_{[2],n+1}-F_{[2],n} \end{array} \right. \end{eqnarray} $$
$3$の倍数項の場合
$\{F_{[1],n}\}$ の3の倍数項からなる数列、つまり次の下線部からなる数列 $\{F_{[3],n}\}$ を考えます。
$\underline{0},1,1,\underline{2},3,5,\underline{8},13,21,\underline{34},55,89,\underline{144},\cdots$
${\displaystyle \{F_{[3],n}\}=\{0,2,8,34,144,610,\cdots\}\qquad(n=0,1,2,3,\cdots)}$
この数列は、次のように三項間漸化式で定義することができます。
$$ \begin{eqnarray} \left\{ \begin{array}{l} F_{[3],0}=0 \\ F_{[3],1}=2 \\ F_{[3],n+2}=4F_{[3],n+1}+F_{[3],n} \end{array} \right. \end{eqnarray} $$
$k$の倍数項の場合
ここまでの例を一般化すると次のようになります。
$\{F_{[1],n}\}$ の $k$ の倍数項からなる数列 $\{F_{[k],n}\}$ を考えます。
${\displaystyle \{F_{[3],n}\}=\{F_{[1],0},F_{[1],k},F_{[1],2k},F_{[1],3k},F_{[1],4k},\cdots\}\qquad(n=0,1,2,3,\cdots)}$
この数列は、次のように三項間漸化式で定義することができます。
$$ \begin{eqnarray} \left\{ \begin{array}{l} F_{[k],0}=0 \\ F_{[k],1}=F_{[1],k} \\ F_{[k],n+2}=L_k F_{[k],n+1}-(-1)^kF_{[k],n} \end{array} \right. \end{eqnarray} $$
フィボナッチ数・リュカ数の連続関数化
上記をさらに一般化して、非整数を含む実数 $a$ に対して「フィボナッチ数の「aの整数倍項」からなる数列」というものを考えたいと思います。
「あれ?項数は整数しかないのでは？」と思われたかもしれません。
そのとおりです。実数の項に当たるものが考えられるようにフィボナッチ数を一般化する必要があります。
そのために、まずはフィボナッチ数の一般項を連続化した関数を考えます。その関数を $f(x)$ とすると、$x$ が整数のときは $f(x)=F_{[1],x}$ となるような関数で、なるべく自然なものを考えたいですね。複素数を使うと、いい感じに連続化することができます。
まずはビネの公式をベースに考えてみましょう。
${\displaystyle \begin{eqnarray} \left\{ \begin{array}{l} F_{[1],n}={\frac {\varphi ^{n}-(-\varphi )^{-n}}{\sqrt {5}}}\\ L_{n}=\varphi ^{n}+(-\varphi )^{-n} \end{array} \right. \end{eqnarray} }$
フィボナッチ数を非整数に対しても定義して連続化したいのですが、負の数のべき乗の部分がじゃまで連続化できなさそうに見えます。しかし、
$e^{i\pi}=-1$
を使って次のように書き換えてみるとどうでしょうか。
${\displaystyle F_{n}={\frac {\varphi ^{n}-\varphi^{-n}e^{i\,n\pi}}{\sqrt {5}}}}$
負の数のべき乗の部分は複素数平面上での回転に変換されて、連続かつ微分可能ないい感じの式になりました。この記事ではこの関数をフィボナッチ数列を一般化した関数として採用し、「連続化フィボナッチ関数」と呼び、$f(x)$ と表記することにします。
${\displaystyle f(x):={\frac {\varphi ^{x}-\varphi^{-x}e^{i\,x\pi}}{\sqrt {5}}}}$
※連続化したものであることが分かりやすいように変数を $n$ から $x$ に変更しています。
また、リュカ数の方も同様の手法で次のように連続関数化して「連続化リュカ関数」と呼び、$l(x)$ と表記することにします。
${\displaystyle l(x):=\varphi ^{x}+\varphi^{-x}e^{i\,x\pi}}$
式の形を見ればわかるように
${\displaystyle \begin{eqnarray} \left\{ \begin{array}{l} F_{[1],n}=f(n) \\ L_{n}=l(n) \end{array} \right. \end{eqnarray} }$
ですから、フィボナッチ数・リュカ数を連続化した関数としてふさわしいと思います。
連続化フィボナッチ関数から作る数列の三項間漸化式
連続化フィボナッチ関数を使えば、先ほどの議論を整数以外に拡張することができます。
実数 $a$の整数倍の場合
ある実数の定数 $a$ に対して次のように定義される数列 $\{F_{[a],n}\}$ を考えます。
$F_{[a],n}=f(an)$
${\displaystyle \{F_{[a],n}\}=\{f(0),f(a),f(2a),f(3a),f(4a),f(5a),f(6a),f(7a),\cdots\}\qquad(n=0,1,2,3,\cdots)}$
$a=1$ の場合は通常のフィボナッチ数になることに注意してください。
この数列は、次のように $f(a),l(a)$ を用いて三項間漸化式で定義することができます。
$$ \begin{eqnarray} \left\{ \begin{array}{l} F_{[a],0}=0 \\ F_{[a],1}=f(a) \\ F_{[a],n+2}=l(a) F_{[a],n+1}-e^{i\,a\pi}F_{[a],n} \end{array} \right. \end{eqnarray} $$
具体例:フィボナッチ数の間隔を３倍に「補間」した数列の三項間漸化式による定義
たとえば $a=\frac{1}{3}$ とすれば、次のようになります。
$F_{\left[\frac{1}{3}\right],n}=f\left(\frac{n}{3}\right)$
${\displaystyle \left\{F_{\left[\frac{1}{3}\right],n}\right\}=\left\{f\left(\frac{0}{3}\right),f\left(\frac{1}{3}\right),f\left(\frac{2}{3}\right),f\left(\frac{3}{3}\right),f\left(\frac{4}{3}\right),f\left(\frac{5}{3}\right),f\left(\frac{6}{3}\right),f\left(\frac{7}{3}\right),\cdots\right\}\qquad(n=0,1,2,3,\cdots)}$
具体的には次のような感じになります。
$\{0,■,■,1,■,■,1,■,■,2,■,■,3,■,■,5,■,■,8,■,■,13,■,■,\cdots\}$
※ ■の部分には何らかの複素数が入りますが、見やすさのために■で表記しています。
連続化フィボナッチ関数を使って、フィボナッチ数を３倍の間隔に「補間した」数列となっていることがわかります。
先ほどの式を使うと、この数列を三項間漸化式で定義することができます。
$$ \begin{eqnarray} \left\{ \begin{array}{l} F_{\left[\frac{1}{3}\right],0}=0 \\ F_{\left[\frac{1}{3}\right],1}=f\left(\frac{1}{3}\right)\\ \qquad\,\,\,\,=\frac {\varphi ^{\frac{1}{3}}-\varphi^{-\frac{1}{3}}e^{\frac{i\pi}{3}}}{\sqrt {5}}\\ F_{\left[\frac{1}{3}\right],n+2}=l(\frac{1}{3}) F_{\left[\frac{1}{3}\right],n+1}-e^{\frac{i\pi}{3}}F_{\left[\frac{1}{3}\right],n}\\ \qquad\qquad=(\varphi ^{\frac{1}{3}}+\varphi^{-\frac{1}{3}}e^{\frac{i\pi}{3}}) F_{\left[\frac{1}{3}\right],n+1}-e^{\frac{i\pi}{3}}F_{\left[\frac{1}{3}\right],n} \end{array} \right. \end{eqnarray} $$
なぜこの式が成立するか
この式が成立する背景には、三項間漸化式についての次の性質があります。
$x$ の二次方程式 $x^2=Ax+B$ が $0$ でない2つの異なる解 $\alpha,\beta$ を持つとする。このとき、複素数列 $\{X_n\}$ について次は同値である。$(n=0,1,2,3,\cdots)$
「三項間漸化式 $X_{n+2}=AX_{n+1}+BX_{n}$が任意の $n$ について成り立つ」
$\Leftrightarrow$
「$X_n$ の一般項は定数$C,D$ を用いて$X_n=C\alpha^n+D\beta^n$ と表現することができる」
証明
$\Rightarrow$ の証明
$X_{n+2}=AX_{n+1}+BX_{n}$
解と係数の関係より $A=\alpha+\beta,B=-\alpha\beta$ であるから、
$\begin{align} (X_{n+2}-\alpha X_{n+1})&=\beta(X_{n+1}-\alpha X_{n})\\ &=\beta^{n+1}(X_{1}-\alpha X_{0}) \end{align}$
同様に
$\begin{align} (X_{n+2}-\beta X_{n+1}) &=\alpha^{n+1}(X_{1}-\beta X_{0}) \end{align}$
$ \begin{eqnarray} \left\{ \begin{array}{l} (X_{n+2}-\alpha X_{n+1})=\beta^{n+1}(X_{1}-\alpha X_{0}) \\ (X_{n+2}-\beta X_{n+1})=\alpha^{n+1}(X_{1}-\beta X_{0}) \end{array} \right. \end{eqnarray} $
辺々引くと
$(\alpha-\beta)X_{n+1}=(X_{1}-\beta X_{0})\alpha^{n+1}-(X_{1}-\alpha X_{0})\beta^{n+1}$
両辺を $(\alpha-\beta)$ で割ると
$X_{n+1}=\frac{X_{1}-\beta X_{0}}{\alpha-\beta}\cdot\alpha^{n+1}-\frac{X_{1}-\alpha X_{0}}{\alpha-\beta}\cdot\beta^{n+1}$
$ \begin{eqnarray} \left\{ \begin{array}{l} C=\frac{X_{1}-\beta X_{0}}{\alpha-\beta} \\ D=-\frac{X_{1}-\alpha X_{0}}{\alpha-\beta} \end{array} \right. \end{eqnarray} $
として、$n$を１つずらせば
$X_n=C\alpha^n+D\beta^n$
を得る。なお、この式は $n=0$ のときも成り立っていることが容易に確かめられる。
$\Leftarrow$ の証明
$ \begin{eqnarray} \left\{ \begin{array}{l} X_{n+1}=C\alpha^{n+1}+D\beta^{n+1} \\ X_n=C\alpha^n+D\beta^n \end{array} \right. \end{eqnarray} $
であり、また、解と係数の関係より $A=\alpha+\beta,B=-\alpha\beta$ であるから、
$\begin{align} AX_{n+1}+BX_{n} &=(\alpha+\beta)(C\alpha^{n+1}+D\beta^{n+1})-\alpha\beta(C\alpha^n+D\beta^n)\\ &=C\alpha^{n+2}+D\alpha\beta^{n+1}+C\alpha^{n+1}\beta+D\beta^{n+2}-C\alpha^{n+1}\beta-D\alpha\beta^{n+1}\\ &=C\alpha^{n+2}+D\beta^{n+2}\\ &=X_{n+2} \end{align}$
$\therefore X_{n+2}=AX_{n+1}+BX_{n}$
これにより、一般項が $X_n=C\alpha^n+D\beta^n$ で表現できる数列は三項間漸化式 $X_{n+2}=(\alpha+\beta)X_{n+1}-\alpha\beta X_{n}$ を満たすことがわかります。
前半部の様々な式はこれを使うことで得られます。良ければ試してみてください。
連続化フィボナッチ関数の複素数範囲での立体グラフ化
連続化フィボナッチ関数 $f(x)$ は、非整数の $x$ に対しては $f(x)$ が複素数範囲になるので、グラフ化するには3つの軸が必要になり立体グラフにすることになります。
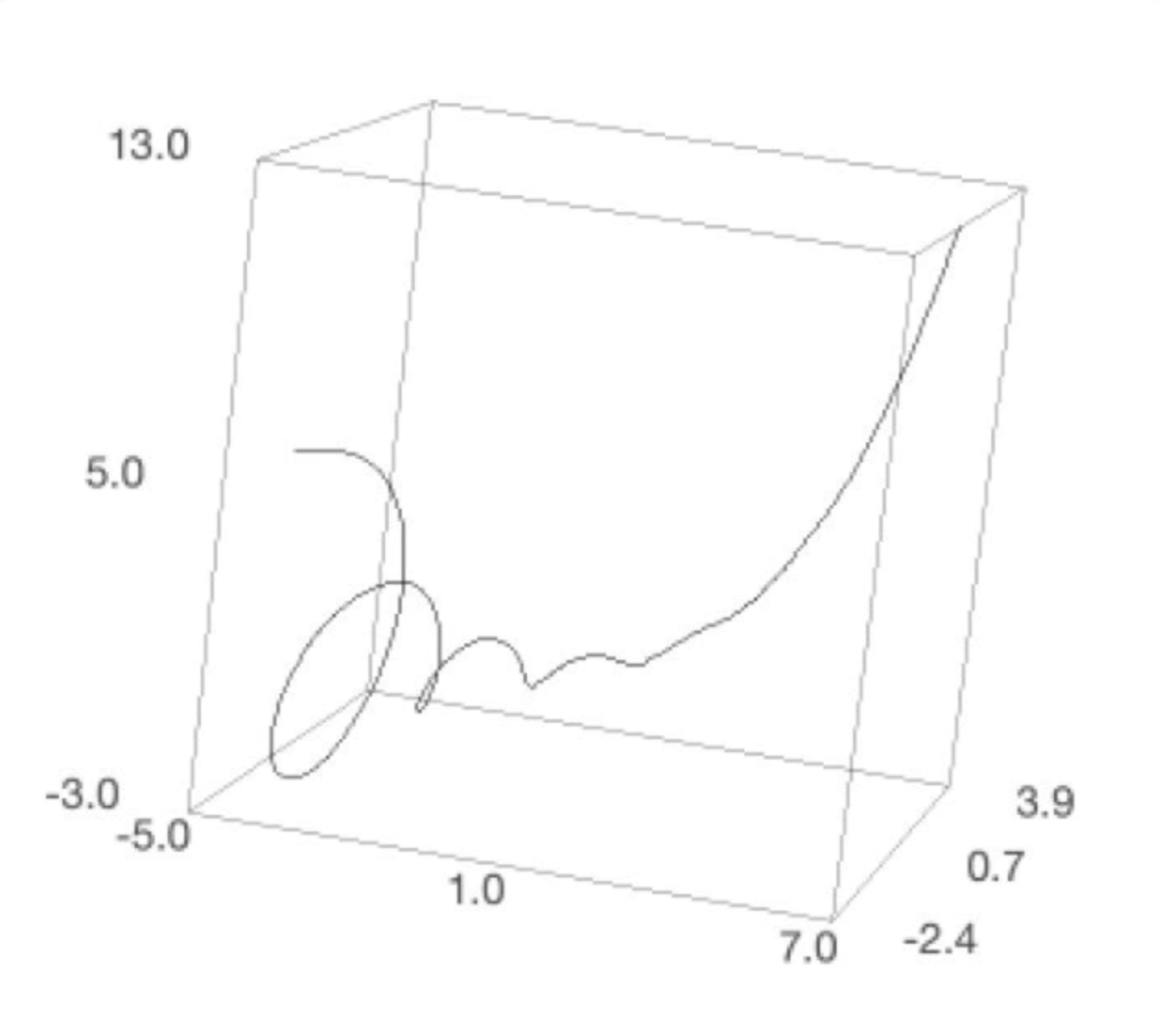連続化フィボナッチ関数を複素数範囲で立体グラフ化
これを見ると、$x$ がマイナスの部分では偏角の回転が強調されて螺旋状になっていることがわかりますね。$x$ がプラスの部分では回転部分の半径が小さくなってほとんどわからなくなっています。
おわりに
今回の記事の肝の部分を再掲します。
$x$ の二次方程式 $x^2=Ax+B$ が $0$ でない2つの異なる解 $\alpha,\beta$ を持つとする。このとき、複素数列 $\{X_n\}$ について次は同値である。$(n=0,1,2,3,\cdots)$
「三項間漸化式 $X_{n+2}=AX_{n+1}+BX_{n}$が任意の $n$ について成り立つ」
$\Leftrightarrow$
「$X_n$ の一般項は定数$C,D$ を用いて$X_n=C\alpha^n+D\beta^n$ と表現することができる」
第$0$項、第$1$項は $C,D$ に依存しますが、 $C,D$ がなんであろうとも、三項間漸化式
については特定できるという性質は面白いと思いませんか？
この記事を高評価した人
この記事に送られたバッジ
投稿者
