無理数の最良近似分数と連分数展開・加比の理・ファレイ数列の関係(前編)
はじめに
この記事では、次のような問題について考えます。
ネイピア数 $e$ の近似分数であって、分母が$300$以下の分数のうちもっとも$e$との差の絶対値が小さいものはなんでしょうか。
ネイピア数の近似値(いわゆる「ふなひとはちふたはちひとはちふたはち」)
$e=2.718281828\cdots$
は既知としてよいです。
この問題を解くために、無理数の最良近似分数を得る方法についての解説をします。
(前編)では、単純に連分数展開を途中で打ち切る方法では得られない最良近似分数が存在することを紹介し、さらに、加比の理を使えばすべての最良近似分数が得られることを紹介します。
(後編)では、連分数展開を途中で打ち切る方法を改良することで、改良前の方法では得られなかった最良近似分数を得ることができることを紹介し、さらに、その方法を使えば、無理数の具体的な値が不明な場合であっても、その無理数の連分数展開が既知であれば最良近似分数を得られることを示す予定です。
この記事は当初「連分数展開では得られない無理数の最良近似分数を加比の理とファレイ数列で得る」のタイトルで公開していましたが、記事公開後、いろいろな情報がTwitterでよせられたり、木村俊一著「連分数のふしぎ」の本を読んだりした結果、当初は連分数展開では得られないと思っていた無理数の最良近似分数について、連分数展開から得る方法もあることがわかりましたので、記事の内容を大幅に加筆修正してタイトルを「無理数の最良近似分数と連分数展開・加比の理・ファレイ数列の関係」に変更したうえ、(前編)(後編)に分けて再構成したものです。
最良近似分数の定義
「最良近似分数」の定義はいろいろ考えられます。この記事では、以下の議論をわかりやすくするため、「第1種最良近似分数」「第2種最良近似分数」の二つを定義します。
この記事で主に話題とする「第1種最良近似分数」はこんな感じです。
無理数 $\omega$ を近似する分数 $\dfrac{P}{Q}$ について， $q< Q$ なるどんな分数 $\dfrac{p}{q}$ に対しても
$ \left|\omega-\dfrac{P}{Q}\right|<\left|\omega-\dfrac{p}{q}\right| $
がなりたつとき，分数 $\dfrac{P}{Q}$ を無理数 $\omega$ の第1種最良近似分数という。
要するに、これより小さい分母ではよりよい近似が得られないということであり、素朴な定義だと思います。
「最良」という言葉から一つしかないようなニュアンスを感じるかもしれませんが、実際には最良近似分数となるような分数は無数にあることに注意してください。
無理数 $\omega$ を近似する分数 $\dfrac{P}{Q}$ が， $q< Q$ なるどんな分数 $\dfrac{p}{q}$ に対しても
$ \left|Q\omega-P\right|<\left|q\omega-p\right| $
がなりたつとき，分数 $\dfrac{P}{Q}$ を無理数 $\omega$ の第2種最良近似分数という。
定義がやや直感的ではないですが、実は第2種最良近似分数は連分数と相性がよく扱いやすいです。
第1種最良近似分数と第2種最良近似分数の違い
第2種最良近似分数は全て第1種最良近似分数になりますが、第1種最良近似分数は第2種最良近似分数になるとは限りません。言い換えると、第2種最良近似分数の方が範囲がせまいということです。そのことは次の不等式からわかります。
$ \left|Q\omega-P\right|<\left|q\omega-p\right| $
$ \dfrac{1}{Q}\left|Q\omega-P\right|<\dfrac{1}{q}\left|q\omega-p\right| \qquad\because\dfrac{1}{Q}<\dfrac{1}{q} $
$ \left|\omega-\dfrac{P}{Q}\right|<\left|\omega-\dfrac{p}{q}\right| $
また、第1種最良近似分数、第2種最良近似分数ともに、分母が大きいものほど無理数との差の絶対値が小さくなります。
この記事では、主に第1種最良近似分数を得る方法について解説します。単に「最良近似分数」としか書いていない場合は、第1種最良近似分数のことを指していると思って読んでください。
「第1種最良近似分数」「第2種最良近似分数」という名称は私のオリジナルではなく、ネットでみかけたものをそのまま真似して使っています。もとは連分数についての教科書「 A. Ya. Khinchin. Continued Fractions. Dover(1997)」で使われていた用語のようです。
連分数展開で主近似分数を得る方法と第2種最良近似分数
例えば、円周率 $\pi$ の近似分数を連分数展開を途中で打ち切る方法で次々と求めると、次のようになります。
$\pi$ は次のように連分数展開できることが知られています。
${\pi=3 + \dfrac{1}{7 + \dfrac{1}{15 + \dfrac{1}{1 + \dfrac{1}{{292 + \dfrac{1}{1 + \dfrac{1}{1 + \cdots}}}}}}} }$
途中で打ち切ると次のように次々と近似分数が得られます。
${3 =\dfrac{3}{1} }$
${3 + \dfrac{1}{7 } =\dfrac{22}{7}=3.1428571428\cdots }$
${3 + \dfrac{1}{7 + \dfrac{1}{15 }} =\dfrac{333}{106}=3.1415094339\cdots }$
${3 + \dfrac{1}{7 + \dfrac{1}{15 + \dfrac{1}{1}}} =\dfrac{355}{113}=3.1415929203\cdots }$
${3 + \dfrac{1}{7 + \dfrac{1}{15 + \dfrac{1}{1 + \dfrac{1}{292 }}}} =\dfrac{103993}{33102}=3.1415926530\cdots }$
${3 + \dfrac{1}{7 + \dfrac{1}{15 + \dfrac{1}{1 + \dfrac{1}{292 + \dfrac{1}{1 }}}}} =\dfrac{104348}{33215}= 3.1415926539\cdots }$
${3 + \dfrac{1}{7 + \dfrac{1}{15 + \dfrac{1}{1 + \dfrac{1}{292 + \dfrac{1}{1 + \dfrac{1}{1 }}}}}} =\dfrac{208341}{66317}=3.1415926534\cdots }$
このように、連分数を途中で止めて作る近似分数を「主近似分数」と呼びます。また、打ち切る位置で順に「第0主近似分数」「第1主近似分数」$\cdots$「第 $n$ 主近似分数」と呼びます。
上記の例を見ると、止める位置を後ろにするほど近似精度が上がっていることが確認できますね。実は、主近似分数について次の事実が知られています。
第2種最良近似分数は主近似分数である。
逆に、主近似分数は一般に第2種最良近似分数である。
(ただし、第0主近似分数(すなわち整数部分)は除く)
証明はこの記事では省略します。「 実数の有理数近似と連分数(詫間電波工業高等専門学校) 」のpdfを参照してください。
さて、前置きが長かったですが、これでようやく準備ができました。
改めて、次の問題を考えてみましょう。
問題
ネイピア数 $e$ の近似分数であって、分母が$300$以下の分数のうちもっとも$e$との差の絶対値が小さいものはなんでしょうか。
ネイピア数の近似値(いわゆる「ふなひとはちふたはちひとはちふたはち」)
$e=2.718281828\cdots$
は既知としてよいです。
この問題は、「第1種最良近似分数のうち、分母が300以下で一番大きいもの」を求めればよいことになります。
第2種最良近似分数はこの問題の解ではない
実はこの問題の解は第1種最良近似分数ですが第2種最良近似分数ではありません。一応、そのことを具体的な計算で確認しておきましょう。
$e$ は次のように連分数展開できることが知られています。
${e=2 + \dfrac{1}{1 + \dfrac{1}{2 + \dfrac{1}{1 + \dfrac{1}{1 + \dfrac{1}{4 + \dfrac{1}{1 + \dfrac{1}{1 + \dfrac{1}{6 + \dfrac{1}{1+\cdots}}}}}}}}} }$
連分数展開を途中でとめることで近似分数を次々と得られます。
${2 + \dfrac{1}{1} = \dfrac{3}{1} }$
${e=2 + \dfrac{1}{1 + \dfrac{1}{2}} = \dfrac{8}{3} }$
${e=2 + \dfrac{1}{1 + \dfrac{1}{2 + \dfrac{1}{1}}} = \dfrac{11}{4} }$
${e=2 + \dfrac{1}{1 + \dfrac{1}{2 + \dfrac{1}{1 + \dfrac{1}{1}}}} = \dfrac{19}{7} }$
${e=2 + \dfrac{1}{1 + \dfrac{1}{2 + \dfrac{1}{1 + \dfrac{1}{1 + \dfrac{1}{4}}}}} = \dfrac{87}{32} }$
${e=2 + \dfrac{1}{1 + \dfrac{1}{2 + \dfrac{1}{1 + \dfrac{1}{1 + \dfrac{1}{4 + \dfrac{1}{1}}}}}} = \dfrac{106}{39} }$
${e=2 + \dfrac{1}{1 + \dfrac{1}{2 + \dfrac{1}{1 + \dfrac{1}{1 + \dfrac{1}{4 + \dfrac{1}{1 + \dfrac{1}{1}}}}}}} = \dfrac{193}{71} }$
この方法で得られる主近似分数(=第2種最良近似分数)を分母が小さい順に並べるとこうなります。
$\dfrac{3}{1},\dfrac{8}{3},\dfrac{11}{4},\dfrac{19}{7},\dfrac{87}{32},\dfrac{106}{39},\dfrac{193}{71},\dfrac{1264}{465},\dfrac{1457}{536},\dfrac{2721}{1001},\cdots$
(実は、$e$ より大きいものと $e$ より小さいものが交互に並んでいます。)
上記の近似分数たちのうち、分母が $300$ 以下で最大なのは $\dfrac{193}{71}$ です。しかし、$\dfrac{193}{71}$ はこの問題の答えではありません。
数値計算で確かめる
具体的な解き方を考える前に、あらかじめ第1種最良近似分数がどのように現れるのかを確認しておきましょう。
| 分母 | 分数 | 誤差 | 最良 |
|---|---|---|---|
| 1 | ${3\over1}$ | -0.28171817 | Y |
| 2 | ${5\over2}$ | 0.21828183 | Y |
| 3 | ${8\over3}$ | 0.051615162 | Y |
| 4 | ${11\over4}$ | -0.031718172 | Y |
| 5 | ${14 \over5}$ | -0.081718172 | - |
| 6 | ${16 \over6}$ | 0.051615162 | - |
| 7 | ${19 \over7}$ | 0.0039961142 | Y |
| 8 | ${22 \over8}$ | -0.031718172 | - |
| 9 | ${24 \over9}$ | 0.051615162 | - |
| 10 | ${27\over10}$ | 0.018281828 | - |
| 11 | ${30\over11}$ | -0.0089908988 | - |
| 12 | ${33\over12}$ | -0.031718172 | - |
| 13 | ${35\over13}$ | 0.025974136 | - |
| 14 | ${38\over14}$ | 0.0039961142 | - |
| 15 | ${41\over15}$ | -0.015051505 | - |
| 16 | ${43\over16}$ | 0.030781828 | - |
| 17 | ${46\over17}$ | 0.012399476 | - |
| 18 | ${49\over18}$ | -0.0039403938 | Y |
| 19 | ${52\over19}$ | -0.018560277 | - |
| 20 | ${54\over20}$ | 0.018281828 | - |
表の右列が「Y」となっているのが第1種最良近似分数で、「-」は第1種最良近似分数ではない近似分数です。第1種最良近似分数を並べると次のとおりです。
$\dfrac{3}{1},\dfrac{5}{2},\dfrac{8}{3},\dfrac{11}{4},\dfrac{19}{7},\dfrac{49}{18},\dfrac{68}{25},\dfrac{87}{32},\dfrac{106}{39},\dfrac{193}{71},\dfrac{685}{252},\dfrac{878}{323},\dfrac{1071}{394},\dfrac{1264}{465},\dfrac{1457}{536},\dfrac{2721}{1001},\cdots$
連分数展開で得られる主近似分数(=第2種最良近似分数)を並べるとこうでした。
$\dfrac{3}{1},\dfrac{8}{3},\dfrac{11}{4},\dfrac{19}{7},\dfrac{87}{32},\dfrac{106}{39},\dfrac{193}{71},\dfrac{1264}{465},\dfrac{1457}{536},\dfrac{2721}{1001},\cdots$
比較すると、連分数展開の主近似分数を得る方法では全ての最良近似分数が得られるわけではないことがわかります。
加比の理で第1種最良近似分数を得る
まず、不等式バージョンの加比の理を説明します。
加比の理(不等式バージョン)
不等式バージョンの加比の理は次のようなものです。
$\dfrac{b}{a} < \dfrac{d}{c}$ のとき $\dfrac{b}{a} <\dfrac{b+d}{a+c} <\dfrac{d}{c} $
この不等式が成立することは次の図から明らかでしょう。
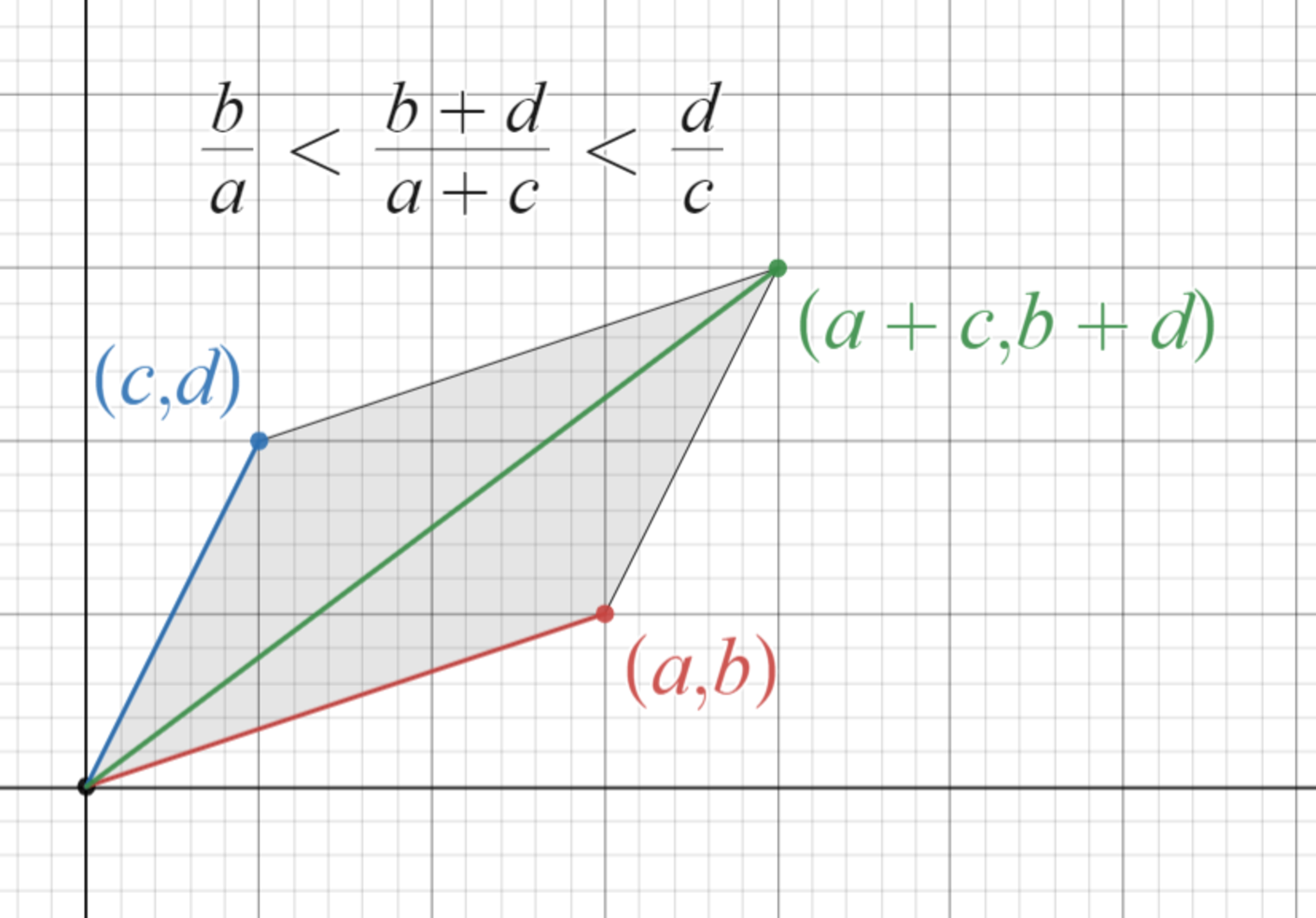加比の理の図形的証明
アルゴリズム
さて、次の作り方で加比の理を使ってどんどん $e$ の近似分数を作っていきます。
(作り方)
次の不等式からスタートする。
${\displaystyle {2 \over 1} < e < {3 \over 1} }$
加比の理で新しい分数を作る。
${\displaystyle {2 \over 1} < {5 \over 2} < {3 \over 1} }$
$e$ との大小を比較して新しい不等式を作る。
${\displaystyle {5 \over 2} < e < {3 \over 1} }$
以下くりかえし
このアルゴリズムで次のように近似分数の不等式が次々と得られます。
${\displaystyle {2 \over 1} < e < {3 \over 1} }$
${\displaystyle {5 \over 2} < e < {3 \over 1} }$
${\displaystyle {8 \over 3} < e < {3 \over 1} }$
${\displaystyle {8 \over 3} < e < {11 \over 4} }$
${\displaystyle {19 \over 7} < e < {11 \over 4} }$
${\displaystyle {19 \over 7} < e < {30 \over 11} }$
${\displaystyle {19 \over 7} < e < {49 \over 18} }$
${\displaystyle {19 \over 7} < e < {68 \over 25} }$
${\displaystyle {19 \over 7} < e < {87 \over 32} }$
${\displaystyle {106 \over 39} < e < {87 \over 32} }$
${\displaystyle {106 \over 39} < e < {193 \over 71} }$
${\displaystyle {299 \over 110} < e < {193 \over 71} }$
${\displaystyle {492 \over 181} < e < {193 \over 71} }$
${\displaystyle {685 \over 252} < e < {193 \over 71} }$
${\displaystyle {878 \over 323} < e < {193 \over 71} }$
${\displaystyle {1071 \over 394} < e < {193 \over 71} }$
${\displaystyle {1264 \over 465} < e < {193 \over 71} }$
${\displaystyle {1264 \over 465} < e < {1457 \over 536} }$
${\displaystyle {2721 \over 1001} < e < {1457 \over 536} }$
${\displaystyle {2721 \over 1001} < e < {4178 \over 1537} }$
実は、それぞれの不等式で
$e\text{より小さいもののうち最良近似}< e< e\text{より大きいもののうち最良近似}$
となっています。つまり、不等式の左右のうち少なくとも片方は第1種最良近似分数になっています。両方が第1種最良近似分数となっている場合もあります。
得られた分数を並べると次のようになります。
$\dfrac{3}{1},\dfrac{5}{2},\dfrac{8}{3},\dfrac{11}{4},\dfrac{19}{7},\dfrac{30}{11},\dfrac{49}{18},\dfrac{68}{25},\dfrac{87}{32},\dfrac{106}{39},\dfrac{193}{71},\dfrac{299}{110},\dfrac{492}{181},\dfrac{685}{252},\dfrac{878}{323},\dfrac{1071}{394},\dfrac{1264}{465},\dfrac{1457}{536},\dfrac{2721}{1001},\cdots$
それでは、第1種最良近似分数、第2種最良近似分数と加比の理で得られた分数を比較してみましょう。
| 第1種 | 第2種 | 加比の理 |
|---|---|---|
| $\dfrac{3}{1}$ | $\dfrac{3}{1}$ | ●$< e$<$\dfrac{3}{1}$ |
| $\dfrac{5}{2}$ | - | $\dfrac{5}{2}$<$e<$● |
| $\dfrac{8}{3}$ | $\dfrac{8}{3}$ | $\dfrac{8}{3}$<$e<$● |
| $\dfrac{11}{4}$ | $\dfrac{11}{4}$ | ●$< e$<$\dfrac{11}{4}$ |
| $\dfrac{19}{7}$ | $\dfrac{19}{7}$ | $\dfrac{19}{7}$<$e<$● |
| - | - | ●$< e$<$\dfrac{30}{11}$ |
| $\dfrac{49}{18}$ | - | ●$< e$<$\dfrac{49}{18}$ |
| $\dfrac{68}{25}$ | - | ●$< e$<$\dfrac{68}{25}$ |
| $\dfrac{87}{32}$ | $\dfrac{87}{32}$ | ●$< e$<$\dfrac{87}{32}$ |
| $\dfrac{106}{39}$ | $\dfrac{106}{39}$ | $\dfrac{106}{39}$<$e<$● |
| $\dfrac{193}{71}$ | $\dfrac{193}{71}$ | ●$< e$<$\dfrac{193}{71}$ |
| - | - | $\dfrac{299}{110}$<$e<$● |
| - | - | $\dfrac{492}{181}$<$e<$● |
| $\dfrac{685}{252}$ | - | $\dfrac{685}{252}$<$e<$● |
| $\dfrac{878}{323}$ | - | $\dfrac{878}{323}$<$e<$● |
| $\dfrac{1071}{394}$ | - | $\dfrac{1071}{394}$<$e<$● |
| $\dfrac{1264}{465}$ | $\dfrac{1264}{465}$ | $\dfrac{1264}{465}$<$e<$● |
この表を見れば、「加比の理を使えば第1種最良近似分数を得られそう」であることがわかります。
また、「第2種最良近似分数は、"$e$ より小さいもの" と "$e$ より大きいもの" が切り替わる直前に現れる」という法則があることもわかります。
さらに、「加比の理を使って得られる近似分数の中には、最良近似分数でないものも含まれている」こともわかりますね。さらに注意深く観察すると、「加比の理を使って得られる近似分数で最良近似分数でないものは、不等式の逆側の近似分数の中に『より分母が小さくて誤差も小さいもの』がある」という法則があることがわかります。
ファレイ数列との関係
それでは、上記の法則の正当性を確認しましょう。
加比の理で近似分数を得るアルゴリズムは、ファレイ数列に現れる無理数の近似分数を順に得る手順と全く一致しています。ファレイ数列の性質から、加比の理で最良近似分数をすべて得られることが理解できるようになります。
ファレイ数列とは、つぎのような一群の数列です。
ファレイ数列とは、既約分数を順に並べた一群の数列である。 正確にいえば、
自然数 $n$ に対して、$n$ に対応する（または、属する）ファレイ数列 (Farey sequence of order $n$) $F_n$ とは、分母が $n$ 以下で、 $0$ 以上 $1$ 以下の全ての既約分数を小さい順から並べてできる有限数列である。 ただし、整数 $0, 1$ はそれぞれ分数 ${0 \over 1},{1 \over 1}$ として扱われる。
ファレイ数列 $F_n$ は、具体的に $n = 1, \ldots, 8$ のとき次のようになります。
$F_1 = \left({0 \over 1},{1 \over 1}\right)$
$F_2 = \left({0 \over 1},{1 \over 2},{1 \over 1}\right)$
$F_3 = \left({0 \over 1},{1 \over 3},{1 \over 2},{2 \over 3},{1 \over 1}\right)$
$F_4 = \left({0 \over 1},{1 \over 4},{1 \over 3},{1 \over 2},{2 \over 3},{3 \over 4},{1 \over 1}\right)$
$F_5 = \left({0 \over 1},{1 \over 5},{1 \over 4},{1 \over 3},{2 \over 5},{1 \over 2},{3 \over 5},{2 \over 3},{3 \over 4},{4 \over 5},{1 \over 1}\right)$
$F_6 = \left({0 \over 1},{1 \over 6},{1 \over 5},{1 \over 4},{1 \over 3},{2 \over 5},{1 \over 2},{3 \over 5},{2 \over 3},{3 \over 4},{4 \over 5},{5 \over 6},{1 \over 1}\right)$
$F_7 = \left({0 \over 1},{1 \over 7},{1 \over 6},{1 \over 5},{1 \over 4},{2 \over 7},{1 \over 3},{2 \over 5},{3 \over 7},{1 \over 2},{4 \over 7},{3 \over 5},{2 \over 3},{5 \over 7},{3 \over 4},{4 \over 5},{5 \over 6},{6 \over 7},{1 \over 1}\right)$
$F_8 = \left({0 \over 1},{1 \over 8},{1 \over 7},{1 \over 6},{1 \over 5},{1 \over 4},{2 \over 7},{1 \over 3},{3 \over 8},{2 \over 5},{3 \over 7},{1 \over 2},{4 \over 7},{3 \over 5},{5 \over 8},{2 \over 3},{5 \over 7},{3 \over 4},{4 \over 5},{5 \over 6},{6 \over 7},{7 \over 8},{1 \over 1}\right)$
ファレイ数列(Wikipediaより)
ファレイ数列の面白い性質(隣接する分数と中間数)
ファレイ数列に新たな分数が加わる法則があります。
$2$ つの分数 $\dfrac{a}{b}$ と $\dfrac{c}{d}$ が、あるファレイ数列で隣接しているならば、この $2$ つの分数の間に新たな分数が加わるのは次数 ${b+d}$ のファレイ数列においてであり、それは $\dfrac{a}{b},\dfrac{c}{d}$ の中間数 (mediant) と呼ばれる分数、
$\dfrac{a+c}{b+d}$
である。
例えば、$F_5$ では隣接している $\dfrac{1}{3}$ と $\dfrac{2}{5}$ の間に現れる最初の項は $F_8$ の
$\dfrac{3}{8}$
です。この中間数の式は加比の理で二つの分数の間にある分数を求める計算式と全く同じであることがわかりますね!
加比の理で最良近似分数が得られる理由
これで、加比の理で最良近似分数が得られる理由がわかります。
具体例で考えましょう。たとえば $F_5$ の中で $(e-2)$ の入る位置を考えると
${0 \over 1}<\cdots<{2 \over 3}<(e-2)<{3 \over 4}<\cdots<{1 \over 1}$
となることから、分母が $5$ 以下の分数のうち、$e$ より小さくて $e$ に最も近い分数は $\dfrac{8}{3}$ で、$e$ より大きくて $e$ に最も近い分数は $\dfrac{11}{4}$ であることがわかります。
次にファレイ数列に$e$に更に近い分数が現れるのは、$3+4=7$ より $F_7$ であることがわかり、$F_7$の中で $(e-2)$ の入る位置を考えると
${0 \over 1}<\cdots<{2 \over 3}<{5 \over 7}<(e-2)<{3 \over 4}<\cdots<{1 \over 1}$
となることから、分母が $7$ 以下の分数のうち、$e$ より小さくて $e$ に最も近い分数は $\dfrac{19}{7}$ で、$e$ より大きくて $e$ に最も近い分数は $\dfrac{11}{4}$ であることがわかります。
問題の答え
ここまでを踏まえて、冒頭の問題を解いてみましょう。
ネイピア数 $e$ の近似分数であって、分母が$300$以下の分数のうちもっとも$e$との差の絶対値が小さいものはなんでしょうか。
ネイピア数の近似値(いわゆる「ふなひとはちふたはちひとはちふたはち」)
$e=2.718281828\cdots$
は既知としてよいです。
$e=2.718281828828\cdots$ と加比の理を使って得られる不等式を再掲します。
${\displaystyle {2 \over 1} < e < {3 \over 1} }$
${\displaystyle {5 \over 2} < e < {3 \over 1} }$
${\displaystyle {8 \over 3} < e < {3 \over 1} }$
${\displaystyle {8 \over 3} < e < {11 \over 4} }$
${\displaystyle {19 \over 7} < e < {11 \over 4} }$
${\displaystyle {19 \over 7} < e < {30 \over 11} }$
${\displaystyle {19 \over 7} < e < {49 \over 18} }$
${\displaystyle {19 \over 7} < e < {68 \over 25} }$
${\displaystyle {19 \over 7} < e < {87 \over 32} }$
${\displaystyle {106 \over 39} < e < {87 \over 32} }$
${\displaystyle {106 \over 39} < e < {193 \over 71} }$
${\displaystyle {299 \over 110} < e < {193 \over 71} }$
${\displaystyle {492 \over 181} < e < {193 \over 71} }$
${\displaystyle {685 \over 252} < e < {193 \over 71} }$
$252+71>300$ ですから、分母が $300$ 以下の分数でこれ以上 $e$ に近いものはありません。
$\dfrac{685}{252}$ と $\dfrac{193}{71}$ を比較すると
$ \left|e-\dfrac{685}{252}\right|=0.0000278\cdots $
$ \left|e-\dfrac{193}{71}\right|=0.0000280\cdots $
ですから、求める最良近似分数は
$\dfrac{685}{252}$
であることがわかります。
おわりに
今回の記事は、M\{R}さんのツイート、ととさんのツイート、しおあびびさんのツイートを参考にさせていただきした。ありがとうございました。
(前編)の記事はここでおしまいです。
(後編)の記事では、連分数展開を途中で打ち切る方法を改良することで、無理数の具体的な値が不明な場合であっても、その無理数の連分数展開が既知であれば最良近似分数を得られることを示す予定です。お楽しみに!
参考文献
この記事を高評価した人
この記事に送られたバッジ
投稿者
