論理と確率のミックスルール、意外と相性よい説!!

本日のプレゼンターは$\cdots$!?

こんにちは！ みゆ🌹ฅ^•ω•^ฅです。本日私が持ってきました説はコチラ。

「論理学と確率論のミックスルール、意外と相性よい説」

論理学といえば、与えられた命題が二種類の論理値のうちの「真」なのか「偽」なのかを判定する「二値論理」をイメージされる方も多いかと思います。一方で、確率論といえばサイコロを１回振って狙った目を出せるかとか、麻雀で九蓮宝燈を天和しちゃうとかの可能性を数値化するってイメージですよね。

この両者、学問カテゴリ上は異なる分野ですが、私の直感的になんとなく相性バッチリな気がしておりまして、せっかくなのでドラゴンボールの合体技のようにフュージョンさせて確率論理というＺ戦士になっていただこうかなと思い立ったというのが経緯です。

$\cdots$何いってるのか自分でもよく分かんなくなってきましたが、実は論理学には三種類以上の論理値を扱う「多値論理」って分野があるんですよ。例えばポーランドの論理学者ヤン・ウカシェヴィチさんは1920年に論理値を三種類にした三値論理というのを提案しておりまして、さらに1930年には無限値論理にまで発展させているんだそうです。

で、私の考える「確率論理」というのは、

$$\quad\frac{真となる場合の数}{起こりうるすべての場合の数}$$

という $0$ から $1$ の範囲の数値、つまり真となる確率（確度）をそのまま論理値としてブール代数的に扱ってしまおうという発想です。この場合、論理値は無限に存在しますので無限値論理ですね。もしかしたら先行研究が既にあるかもしれませんが、それを調べるより自由研究する方が$e$倍楽しいので、さっそく知的創造しながら「説」を検証していきたいと思います♪♪

確率論理演算

否定 (NOT)

確度 $P$ の事象における不確実度（不確かさ）です。

$\lnot P=1-P$
NOT

論理積 (AND)

確度 $P$ の事象と確度 $Q$ の事象が両方とも真である確度です。

$P\land Q=P\cdot Q$
AND

排他的論理和 (XOR)

確度 $P$ の事象と確度 $Q$ の事象のいずれか一方のみが真である角度です。

\begin{align}P\veebar Q&=(P-P\cdot Q)+(Q-P\cdot Q)\\&=P+Q-2(P\cdot Q)\end{align}
XOR

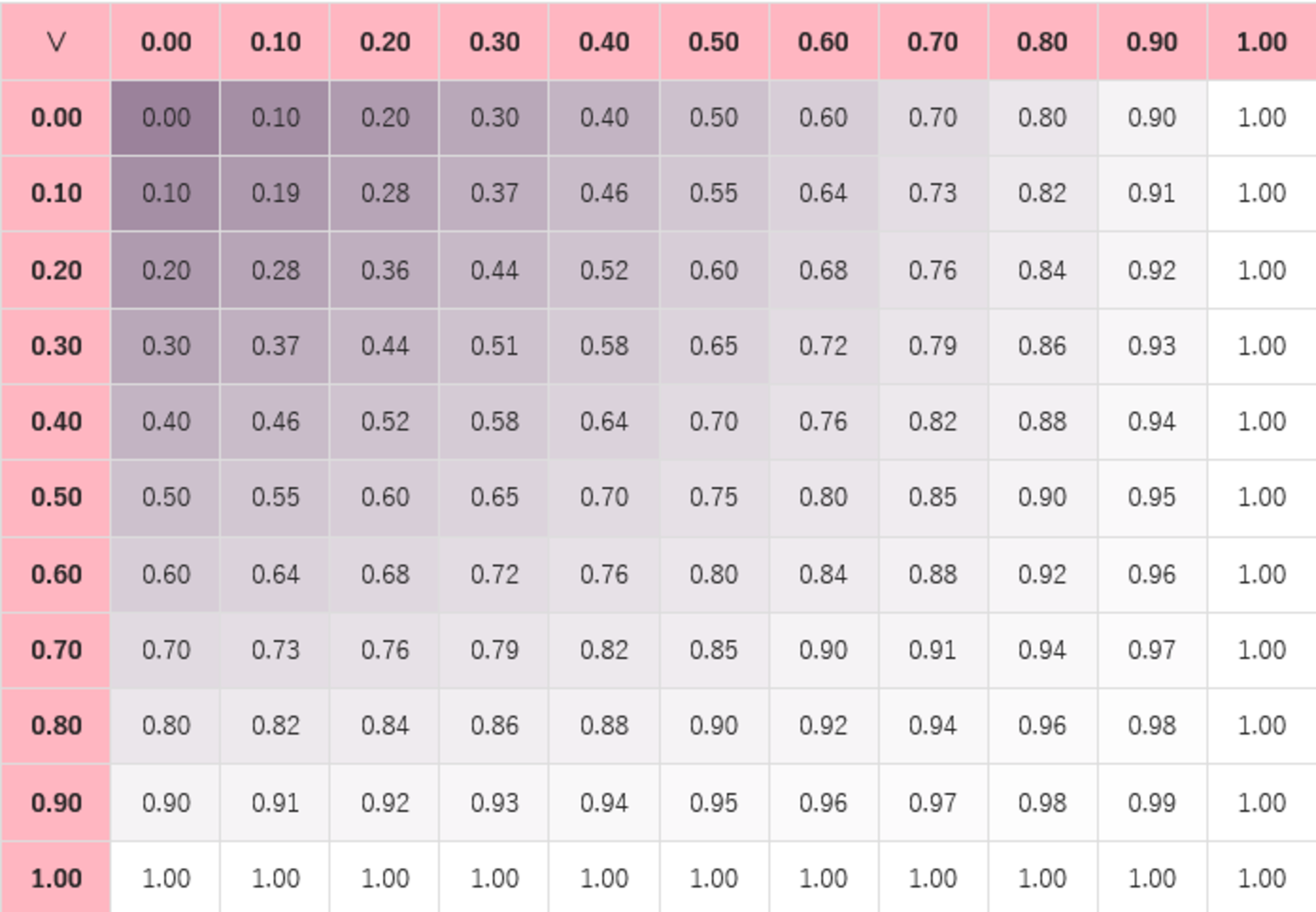
論理和 (OR)

確度 $P$ の事象と確度 $Q$ の事象のいずれか一方あるいは両方ともに真である角度です。

\begin{align}P\lor Q&=(P-P\cdot Q)+(Q-P\cdot Q)+(P\cdot Q)\\&=P+Q-(P\cdot Q)\end{align}
OR

論理包含 (IMP)

確度 $P$ で発生する問題事象に対して確度 $Q$ で回避できる対策をとった場合、結果として問題事象が発生しない確度です。或いは、確度 $P$ で発生する条件事象に対して確度 $Q$ で実現可能な約束をした場合に違約とならない確度です。
※$P$ と $Q$ は互いに独立しており、互いの結果に影響を受けて値が変動することはない点に注意！

\begin{align}P\Rightarrow Q&=(1-P)+(P\cdot Q)\\&=(1-P)+Q-(1-P)\cdot Q\\&=\lnot P\lor Q\end{align}
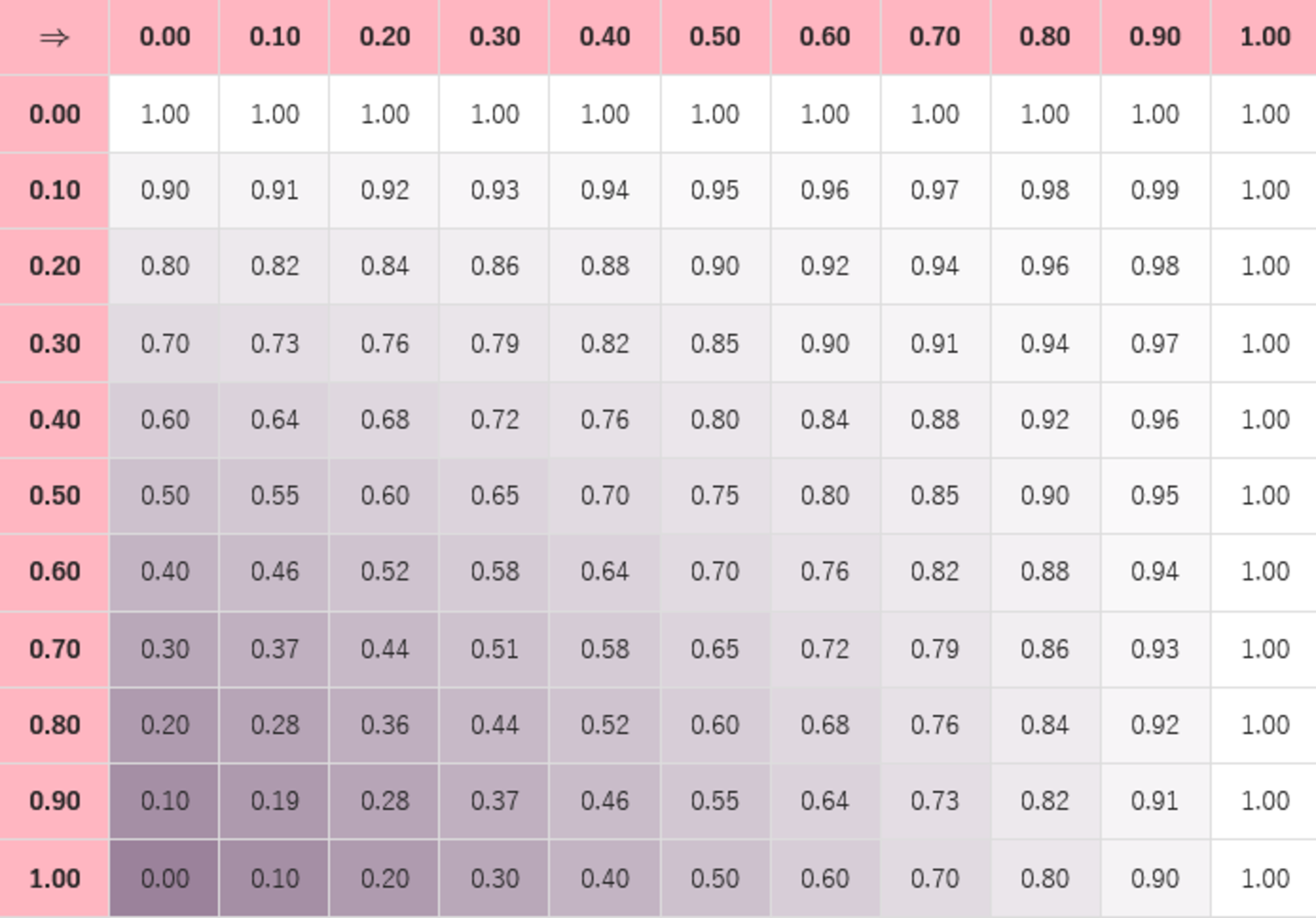IMP

確率論理における各種法則

二値論理でよく知られている法則が、確率論理ではどうなってしまうのか検証してみました。

交換則

常に成立します。

$\begin{align}P\land Q=Q\land P\\P\lor Q=Q\lor P\end{align}$

結合則

常に成立します。

$\begin{align}P\land(Q\land R)=(P\land Q)\land R\\P\lor(Q\lor R)=(P\lor Q)\lor R\end{align}$

ド・モルガンの法則

常に成立します。

$\begin{align}\lnot(P\land Q)=\lnot P\lor\lnot Q\\\lnot(P\lor Q)=\lnot P\land\lnot Q\end{align}$

排中律・無矛盾律

$P$ が $0$ か $1$ の場合にのみ確実に真となります。確度 $P$ の事象が真であるか、
または真でなかった場合にリトライしてもやはり真ではない確度と解釈できます。

$\begin{align}P\lor\lnot P&=P+(1-P)-P\cdot(1-P)\\&=1-P\cdot(1-P)\\&=\lnot(P\land\lnot P)\end{align}$

冪等則

$P$ が $0$ か $1$ の場合にのみ $P$ となります。

$\begin{align}P\land P&=P\cdot P\\&=P-P\cdot(1-P)\end{align}$

$\begin{align}P\lor P&=P+P-P\cdot P\\&=P+(1-P)\cdot P\end{align}$

論理積の吸収則

$P$ が $0$ か $1$ の場合か、$Q$ が $1$ の場合にのみ $P$ となります。

$\begin{align}P\land(P\lor Q)&=P\cdot(P+Q-P\cdot Q)\\&=P-P\cdot(1-P)\cdot(1-Q)\end{align}$

論理和の吸収則

$P$ が $0$ か $1$ の場合か、$Q$ が $0$ の場合にのみ $P$ となります。

$\begin{align}P\lor(P\land Q)&=P+(P\cdot Q)-P\cdot(P\cdot Q)\\&=P+P\cdot(1-P)\cdot Q\end{align}$

論理積の分配則

$P$ が $0$ か $1$ の場合か、$Q$ か $R$ が $0$ の場合にのみ成立します。

$\begin{align}P\land(Q\lor R)=(P\land Q)\lor(P\land R)-P\cdot(1-P)\cdot(Q\land R)\end{align}$

論理和の分配則

$P$ が $0$ か $1$ の場合か、$Q$ と $R$ が $0$ の場合にのみ成立します。

$\begin{align}P\lor(Q\land R)=(P\lor Q)\land(P\lor R)+P\cdot(1-P)\cdot(Q\lor R)\end{align}$

作用差異

確度 $P$ の事象に対して確度 $Q$ の事象を用いて何らかの作用（演算）を行った場合、元の確度 $P$ からどの程度の確度差があるかを示しています。

$\begin{align}P\land Q=P-P\cdot(1-Q)\\P\lor Q=P+(1-P)\cdot Q\end{align}$

実用編

確率論理の特徴は、論理値がそのまま確度すなわち確率として導出されるという点です。

例として、通常の二値論理における論理包含「$P\Rightarrow Q$」について考えてみましょう。

$Q$ が偽であれば $P\Rightarrow Q$ の取りうる値は $P$ の値に左右されますよね。

具体的には、$P$ が偽となる確率が $\frac12$ ならば $P\Rightarrow Q$ が真となる確率も当然 $\frac12$ と言えるわけです。このことをもう少し踏み込んで確率論理で考えてみますと、$Q=0$ においては
$$P\Rightarrow0=1-P$$
であると言うことができます。

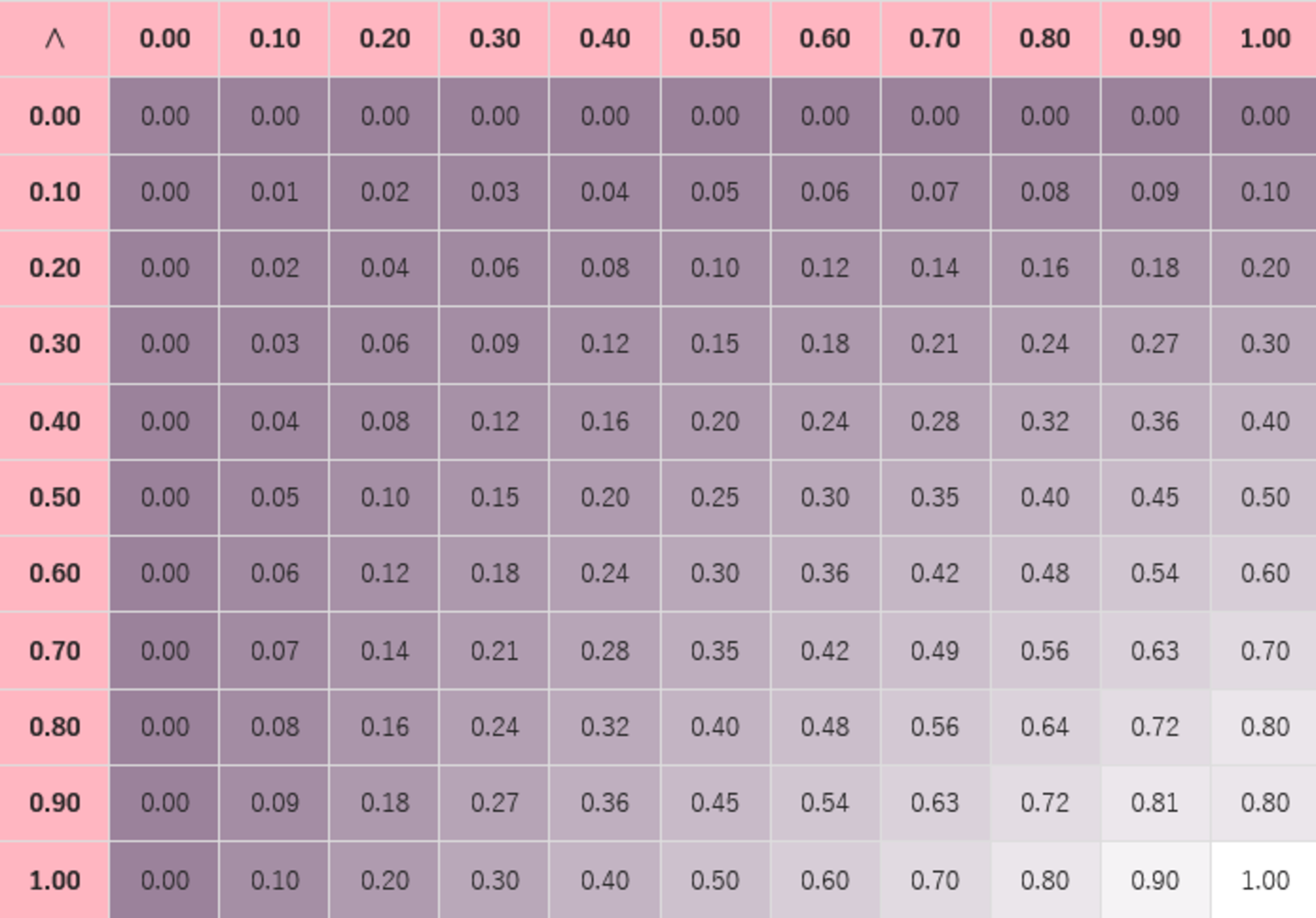
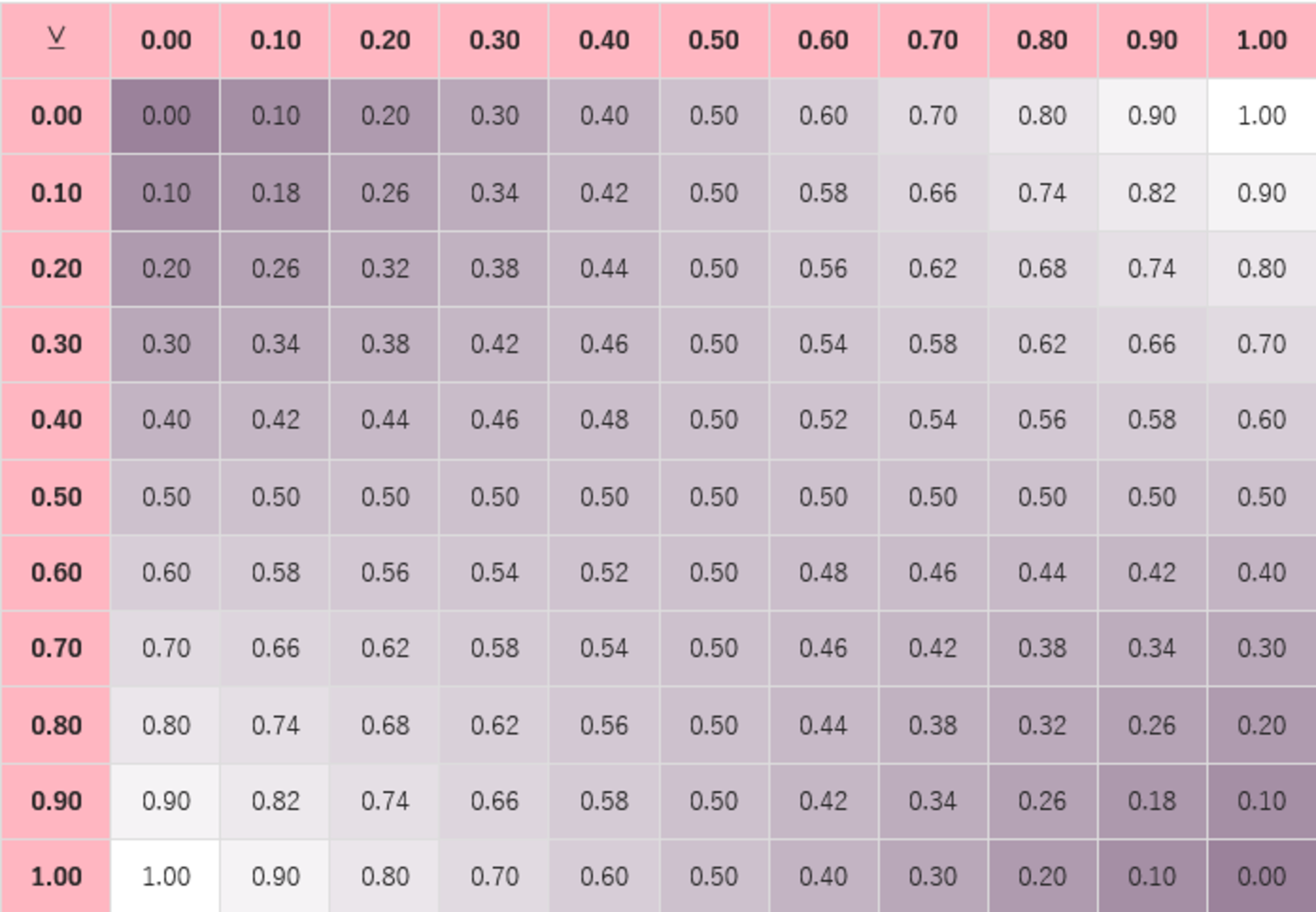
では、$P=\frac12$、$Q=\frac12$ である場合はどうなるでしょうか？ これは、上の表の全４通りの組み合わせのうち真であるケースは何通りかという問題に等価ですので、全４通り中３通りということで確度は $\frac34$ なわけです。確率論理的には
$$\textstyle\frac12\Rightarrow\frac12=\frac34$$
と表せることを意味します。

もっと複雑なケースではどうでしょう。同様に数え上げていけばよいことは言うまでもありませんが、そんな手間のかかることをしなくても確率論理演算を応用すればカンタンに計算できてしまいます。先程の $P=Q=\frac12$ のケースであれば

$\begin{align}P\Rightarrow Q&=(1-P)+P\cdot Q\\&=(1-0.5)+0.5\times0.5=0.75\end{align}$

と瞬殺ですね。

では、実際にありそうな演習問題を試してみましょう。

まず、「傘を差せずに雨に濡れる」という被害が発生しない確度を考えます。これは「雨が降る」という問題が発生しないか、あるいは問題に対する対応策「傘を指す」を実践できない確率ということになりますよね。傘を指せる確度は $(1-0.1)=0.9$ ですから確率論理演算を用いて

ということで、答えは $4$％ です。

検証結果

確率論理演算も各種法則もバッチリ整合性が取れているようで、これはもう

「説、立証」

まだまだ研究の余地はありますが、当初の直感通りの融合に成功しました☆彡
いつもお読みいただいている読者の皆様に心より感謝申し上げますm(_ _)m

最後に、ちょっぴりオマケを書き残しておきますね。

☆★☆ オマケの考察 ☆★☆

通常の二値論理における排他的論理和の特徴として、
$$\quad\begin{align}P\veebar真\equiv\lnot P\end{align}$$
というものがありますよね。

コンピュータ計算では、任意のビット列の特定ビットを反転させる目的で使用されることが多く、レガシーな処理系ではこれを用いて疑似スプライト機能を実現したり、メモリ上にある同サイズのデータをスタックを介さずにスワップ（入れ替え）させたり・・・と何かと役に立つ演算です。

反転させるたびに $1$ との排他的論理和をとりまくることになるわけですが、$0$ との排他的論理和をとっても値は一切変化はしません。では、$0\lt Q\lt1$ の範囲で排他的論理和を取り続けたら論理値はどこに向かうでしょう。

この知的好奇心を満たすため、次のように考察して検証をしてみました。

$$\begin{align}P\veebar Q&=P+Q-2PQ\\&=P(1-2Q)+Q\end{align}$$

であることから、初項 $P_0$ として

$$\begin{align}P_1&=P_0(1-2Q)+Q\\P_n&=P_0(1-2Q)^n+Q\cdot\sum_{k=0}^{n-1}(1-2Q)^{k}\\\lim_{n\to\infty}P_n&=P_0\lim_{n\to\infty}(1-2Q)^n+Q\cdot\lim_{n\to\infty}\sum_{k=0}^{n-1}(1-2Q)^{k}\end{align}$$

$0\lt Q\lt1$ という条件より、$|1-2Q|\lt1$ と限定できますので

$$\begin{align}\lim_{n\to\infty}P_n=P_0\cdot0+\frac{Q}{1-(1-2Q)}=\frac{1}{2}\end{align}$$

なんと、任意の $P$ に対して $0\lt Q\lt1$ の $Q$ でひたすら排他的論理和をとり続けると、$P$ の値に関わらず $0.5$ へと収束することが分かりました。これってつまり、たとえ $Q=\displaystyle\lim_{n\to\infty}\left(1-\frac{1}{n}\right)$ と $1$ に限りなく近づけたとしても、ゲンミツに $Q=1$ ではない限り $0.5$ へと収束してしまうってことですよね。

なんだか、$\begin{cases}\displaystyle\lim_{n\to\infty}\textstyle1^n=1\\\displaystyle\lim_{n\to\infty}\textstyle\left(1-\frac{1}{n}\right)^n=\frac{1}{e}\end{cases}$ に通ずる神秘を感じませんか？