文献あり

わたしの好きな数学の〇〇

636

はじめに

たまに好きな定理とか公式とかを聞かれませんか？思い出すために毎度過去にしたTwitter($\mathbb{X}$)の投稿をさかのぼることにならないように, ここへまとめておくことにしました.
しかもTwitter($\mathbb{X}$)などのプロフィールにはこの記事へのリンクを貼ればいいということになりますからね！

好きな数

いちおう「数学をやっている人間」の端くれではあるので, 「好きな"数"はなあに？」と聞かれたら複素数含めありとあらゆる数から選びます.
では数学界で人気な円周率$\pi$かというと, それもそれでありきたりなのでつまんないなと思ってしまうのがわたしというひとです. ただしもちろん計算の答えとして$\pi$が登場したら嬉しいですよ.

わたしの好きな数はレムニスケート周率$\varpi$です。

$$\varpi=\frac{\Gamma\left(\frac{1}{4}\right)^2}{2\sqrt{2\pi}}=2.6220575542\cdots$$

上記の11桁は覚えています. 一方の円周率$\pi$は35桁($3.1415926535897932384626433832795028$)覚えているので悔しいです.
まだ記録更新してません(2023/10/31時点).

いちおう言っておくと$\Gamma(z)$はガンマ関数という関数です.

少し掘り下げます.
どちらも「〇〇周率」ですが, そこ以外にもちゃんと似た側面があります. 両方の値の積分表示にはそれぞれこのような表示があります:

$$\pi=2\int_0^1\frac{dx}{\sqrt{1-x^2}}$$
$$\varpi=2\int_0^1\frac{dx}{\sqrt{1-x^4}}$$

そっくりですよね. どちらも広義積分ですが, 円周率のほうは高校数学の知識で計算を理解できます.
一方, $x$の指数を$2$から$4$に変えただけでその顔は豹変し, 初等関数で答えが出ない積分になってしまいます.
たしかに, 上記でレムニスケート周率はガンマ関数で表されていましたよね.

次に, 「レムニスケート周率」というぐらいですから当然「レムニスケート」という図形が存在します. 方程式は,
$$ r^2=a^2\cos(2\theta)$$
または
$$(x^2+y^2)^2-2a^2(x^2-y^2)=0$$
となり, グラフはこのようになっています:

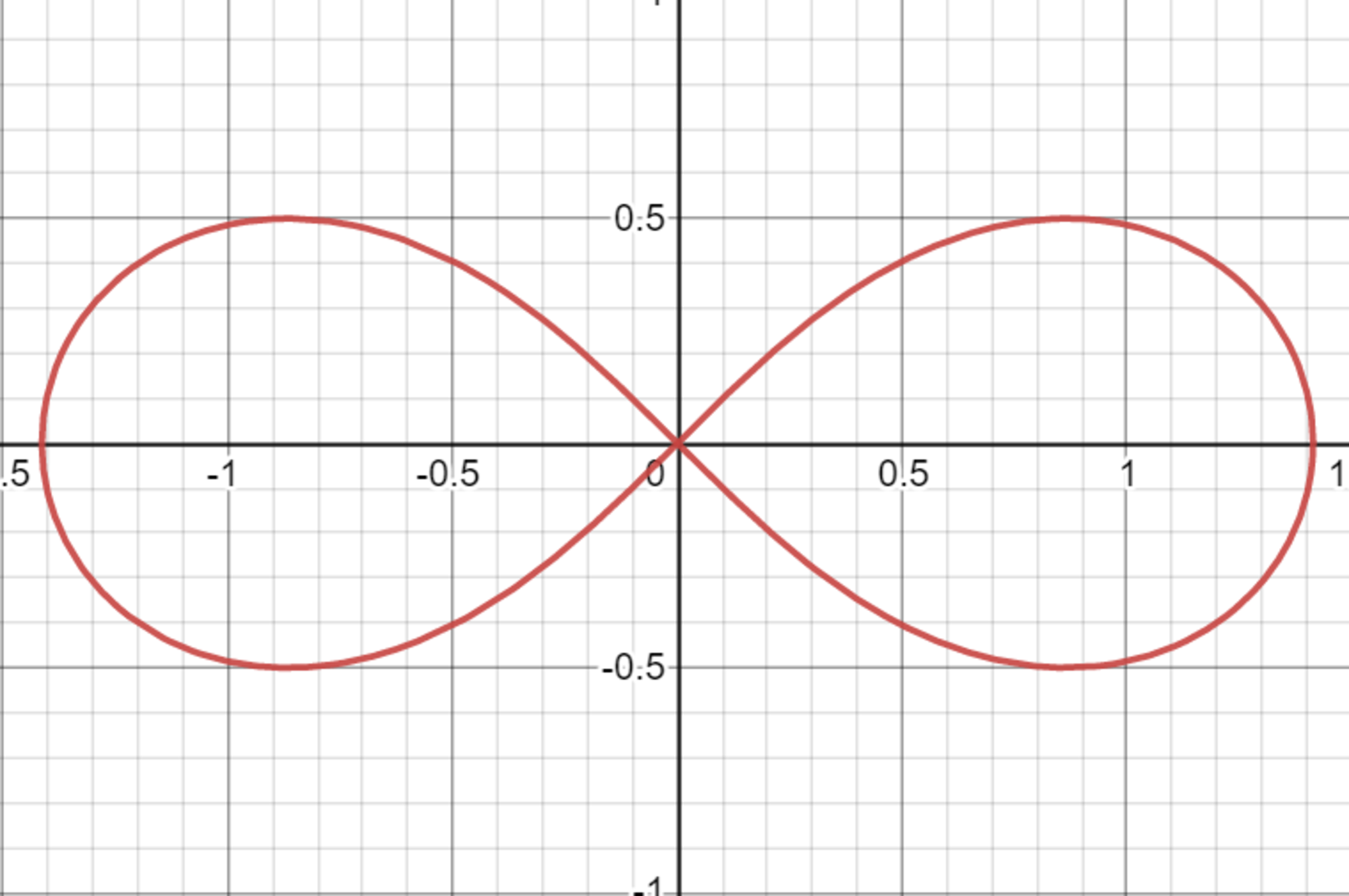レムニスケートのグラフ

ちなみに囲まれている部分の面積は$2a^2$で, $a=1$のとき周の長さが$\varpi$となります.

最後にもう一つ.「$\varpi$」は$\pi$の異体字で, 「ファイ」に$\phi$と$\varphi$があるのと同じです. $\LaTeX(\TeX)$では「\varpi」で出せます.

好きな式とその値

これは, 見た目の初見殺し感と美しさを兼ね備えているところが好きな式です.

$$\lim_{n\to\infty}\frac{!n}{n!}=e^{-1}$$

$!n$というのはモンモール数というものであり, $n$個の要素の完全順列の総数です. 式での表現は次のようになります:

$$ !n=n!\sum_{k=0}^n\frac{(-1)^k}{k!}\qquad(n\geq 0)$$

この表示と, $e^x$のマクローリン展開より, 簡単に先ほどの極限が求まりますね.

好きな問題

● 斬新な$\sum$の使い方

中学生のころ, 先取りをしていて長い間全く分からなかった問題です.

(1)
$$\lim_{n\to\infty}\sum_{k=2n+1}^{3n}\frac{1}{k}$$
(2)
$$\lim_{n\to\infty}\sum_{k=0}^{3n-1}\frac{1}{2n+k}$$

こんなヘンな$\sum$の使い方, 是非とも習得したい！と思った出会いから, 先生に質問して解き方が分かるまで数年間ずっと気になり続けた謎だったので, わかったときはとても嬉しかったのを覚えています.

解答・解説

(1)
そのままでは全く分からないので, $k$へ実際に代入して考えます. ここで忘れてはいけないのは, $k$は$1$ずつ増えるということですね.
「$k$が$2n+1$から$1$ずつ増えていって, 最終的に$3n$になればいい」ので

$\displaystyle\sum_{k=2n+1}^{3n}\frac{1}{k}=\frac{1}{2n+1}+\frac{1}{2n+2}+\cdots+\frac{1}{2n+n}$

こういうことです。つまり

$\displaystyle =\sum_{k=1}^n\frac{1}{2n+k}$

こう書き直すことができますね.
そしたらあとは$\displaystyle\frac{1}{n}$をくくりだして区分求積ですね. 答えは$\displaystyle\ln\frac{3}{2}$です.
(2)
次も同じようにできます. しかも(1)の後半に出てきた形と似ていますね.

$\displaystyle\sum_{k=0}^{3n-1}\frac{1}{2n+k}=\frac{1}{2n}+\frac{1}{2n+1}+\cdots+\frac{1}{3n}+\frac{1}{3n+1}+\cdots+\frac{1}{5n-1}$

ただ, 完全に同じ考え方をする問題を二つ並べることはないので, こちらはひと工夫いるようになっています.
いくつかのカタマリに分けられそうなのがわかるでしょうか？ $k=0$がスタートのときは$n-1$で終われば都合がいいというところから,

$\displaystyle =\sum_{k=0}^{n-1}\frac{1}{2n+k}+\sum_{k=0}^{n-1}\frac{1}{3n+k}+\sum_{k=0}^{n-1}\frac{1}{4n+k}$

となって, あとは区分求積です. 答えは$\displaystyle\ln\frac{5}{2}$になります.

この問題は$\sum$の意味を改めて考えさせる問題でしたね. 初めて見た当時, わたしは公式しか頭になかったので, 展開して方法を見出すという発想はありませんでした.

● 美しくてカッコイイ整数問題

わたしは何かと整数系の問題は無条件にカッコイイと思っている傾向があるみたいです. わかりませんか？

次を満たす自然数の組$x,\ y,\ z$をすべて求めよ.
$$\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1\qquad(x\leq y\leq z)$$

解答・解説

$\displaystyle x\leq y\leq z\ \Longleftrightarrow\ \frac{1}{x}\geq\frac{1}{y}\geq\frac{1}{z}$

だから,

$\displaystyle 1=\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\leq\frac{1}{x}+\frac{1}{x}+\frac{1}{x}=\frac{3}{x}\ \Longleftrightarrow\ x\leq 3$

ここまでの過程もすごい好きです. これ考えたひと天才, って感じです.
(1) $x=1$のとき

$\displaystyle\frac{1}{1}+\frac{1}{y}+\frac{1}{z}=1\ \Longleftrightarrow\ y+z=0$

$y,\ z$は自然数なので, これを満たす$y,\ z$は存在しません.
(2) $x=2$のとき

$\displaystyle\frac{1}{2}+\frac{1}{y}+\frac{1}{z}=1\ \Longleftrightarrow\ yz-2y-2z=0$
$\ \Longleftrightarrow\ (y-2)(z-2)=4$

不定方程式を解くと,
$(y,z)=(3,6),\ (4,4)$. ※ $y\leq z$に注意
(3) $x=3$のとき

$\displaystyle\frac{1}{3}+\frac{1}{y}+\frac{1}{z}=1\ \Longleftrightarrow\ 2yz-3y-3z=0$
$\Longleftrightarrow\ (2y-3)(2z-3)=9$

同じく不定方程式で,
$(y,z)=(3,3)$.
よって, (1)～(3)より$(x,y,z)=(2,3,6),\ (2,4,4),\ (3,3,3)$が答えとなります.

□

● 超難問な整数(有理数)問題

これらがすべて平方数($\in\mathbb{Q}$)となるような正の有理数の組$x,y,z$をひとつ求めよ.
$$ x^2\pm(x+y+z)$$
$$ y^2\pm(x+y+z)$$
$$ z^2\pm(x+y+z)$$

「平方数($\in\mathbb{Q}$)」に気を付けてください. だいたい自然数のものを指すことが多いですが, 今回は例えば$\displaystyle\frac{4}{9}=\left(\frac{2}{3}\right)^2$も平方数だと言えるということです.
あとこれは歴史中でも有名な超難問です.

解答・解説

解答は引用させてください......

　直角３角形（直角をはさむ２辺が$a$と$b$, 斜辺が$c$）では, $c^2=a^2+b^2$
　ゆえに, $c^2\pm 2ab=(a\pm b)^2$
　そこで, 面積が等しい３つの３角形（下図）を用います（なぜそうなるかはすぐにわかります）。

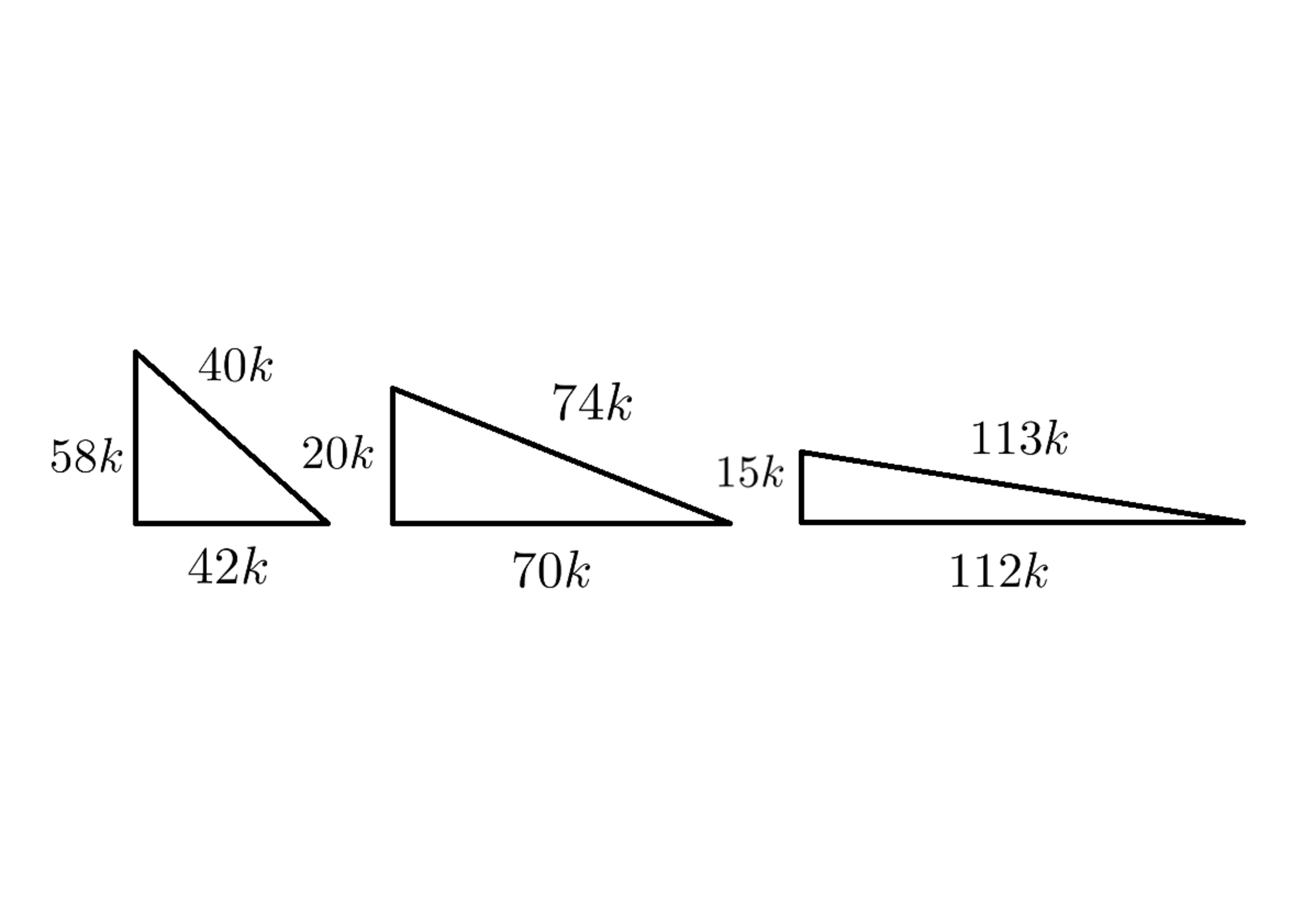面積が等しい三つの三角形

$$(58k)^2\pm \underline{2\cdot 42\cdot 40}k^2=(42\pm 40)^2k^2$$
$$(74k)^2\pm \underline{2\cdot 70\cdot 24}k^2=(70\pm 24)^2k^2$$
$$(113k)^2\pm \underline{2\cdot 112\cdot 15}k^2=(112\pm 15)^2k^2$$
アンダーライン部分はどれも$3360$（面積が等しい３角形を使ったので当然）
　$x+y+z=3360k^2,x=58k,y=74k,z=113k$とおけば題意は満たされる。
　これらより,
$$ 3360k^2=58k+74k+113k=245k$$
$$\therefore\quad k=\frac{7}{96}$$
したがって, $\displaystyle(x,y,z)=\left(\frac{203}{48},\frac{259}{48},\frac{791}{96}\right)$

(以上が[1])

この問題は, 一見関係ない分野のもの(今回は三角形)を用いて解くという突飛なところが大好きです.

● 整数の難問・再び

1990 IMO 問3

$\displaystyle\frac{2^n+1}{n^2}$が整数となるような$1$より大きい整数$n$を全て求めよ.

知る人ぞ知る「マスターデーモン」と呼ばれている問題です.
この問題の回答は長いので割愛します.「マスターデーモン」で調べればすぐに出ると思います.

これの何が好きかというと, 単純な表情をしてその裏の顔は圧倒的な難易度を誇るという系譜の問題が単に好きだからです. まさに数学のおもしろいところですよね.
フェルマーの最終定理のような, もっと"大きな問題"はそういうのばかりでは？というのはたしかにそうなんですが, これぐらいの"スケール"がいいんだと思います(伝われ).

好きな公式

$$\sec^2x+\csc^2x=\sec^2x\csc^2x$$

この式は自力で見つけたので愛着があります. 当初は計算ミスを疑いましたね笑.
念のため言っておくと, $\displaystyle\sec x=\frac{1}{\cos x}, \csc x=\frac{1}{\sin x}$です.

証明

工夫もなにもないですが.
\begin{align*} \text{(左辺)}&=\frac{1}{\cos^2 x}+\frac{1}{\sin^2 x}\\ &=\frac{\sin^2 x+\cos^2 x}{\sin^2 x\cos^2 x}\\ &=\frac{1}{\sin^2 x}\cdot\frac{1}{\cos^2 x}\\ &=\text{(右辺)} \end{align*}

□

好きな定理

二年生の夢 (Sophomore's Dream)

$$\int_0^1\frac{1}{x^x}dx=\sum_{n=1}^\infty\frac{1}{n^n}$$
$$\int_0^1x^xdx=-\sum_{n=1}^\infty(-n)^{-n}$$

証明

$\displaystyle x^{-x}=\textrm{exp}(-x\ln x)=\sum_{n=0}^\infty\frac{(-x\ln x)^n}{n!}=\sum_{n=0}^\infty\frac{(-x)^n\ln^nx}{n!}$

両辺を$0$から$1$まで積分します. $\sum$と$\int$の交換に注意します.

$\displaystyle\int_0^1x^{-x}dx=\int_0^1\sum_{n=0}^\infty\frac{(-x)^n\ln^nx}{n!}dx$
$\displaystyle\int_0^1\frac{1}{x^x}dx=\sum_{n=0}^\infty\frac{(-1)^n}{n!}\int_0^1x^n\ln^nx\,dx$

右辺の積分は$\ln x=-t$と置換すると,

$\displaystyle(\textrm{右辺})=\sum_{n=0}^\infty\frac{(-1)^{2n}}{n!}\int_0^\infty t^ne^{-(n+1)t}dt$

$\displaystyle t\longmapsto\frac{t}{n+1}$とすれば,

$\displaystyle=\sum_{n=0}^\infty\frac{1}{n!}\frac{1}{(n+1)^n}\int_0^\infty t^{n}e^{-t}\frac{dt}{n+1}$
$\displaystyle=\sum_{n=0}^\infty\frac{1}{n!}\frac{1}{(n+1)^{n+1}}\int_0^\infty t^{(n+1)-1}e^{-t}dt$

残った積分はガンマ関数なので,

$\displaystyle=\sum_{n=0}^\infty\frac{1}{n!}\frac{\Gamma(n+1)}{(n+1)^{n+1}}=\sum_{n=0}^\infty\frac{1}{(n+1)^{n+1}}=\sum_{n=1}^\infty\frac{1}{n^n}$

よって$\displaystyle\int_0^1\frac{1}{x^x}dx=\sum_{n=1}^\infty\frac{1}{n^n}$.
もう一つも同様に示すことができます.

好きな証明

これは非常に天才的ですばらしい証明だと思っていて, いろんなひとにこの証明の話をしたことがあります.

調和級数の発散

$$\sum_{n=1}^\infty\frac{1}{n}=\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots=\infty$$

\begin{align*} \textrm{(左辺)}&=\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}+\cdots\\ &>\frac{1}{1}+\frac{1}{2}+\frac{1}{4}+\frac{1}{4}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\cdots\\ &=1+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\cdots\\ &=\infty \end{align*}
追い出しの原理より, 左辺は発散します.

□