「真っすぐになれ」と言われ続けてイライラした件について

「もっと真っすぐになれ」

それは、僕が中学生だった頃、野球部でキャッチボールをしているときに言われました。

アップで2人1組でキャッチボールをするのですが、このとき2人は平行になるという暗黙のルールがありました。

いや、理由はわかります。

隣同士ぶつかったら危ないですもんね。

わかりますけども。

謎に厳しいんですよ。

ちょっとずれただけで「真っすぐになれ」と相方から言われるんです。

しかも、僕は自身がずれてるということがわからないんですよ。

だって2点あれば直線ができるから、ずれるもなにもないじゃないですか。

確かに僕はへそ曲がりかもしれないですけども。

空間上に点が2つあれば直線ができる

※点を2つ置くと直線ができるのは$\mathbb{R}^n$上でも言えるのですが、今は平面を考えます。

平面上に点を2つ置くと、直線ができます。

2点をそれぞれ$A:(x_{1}, y_{1}), B:(x_{2}, y_{2})$とすると、直線の方程式は以下のように表せます。

$$(y - y_{1}) = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}(x - x_{1})　(x_{1}≠x_{2})$$

例えば、$x = x_{1}, y = y_{1}$を代入すると、両辺が$0$になり、等式が成り立ちます。

また、$x = x_{2}, y = y_{2}$を代入しても、等式が成り立ちます。

さらに、傾きは$\frac{y_{2} - y_{1}}{x_{2} - x_{1}}$で表せます。

なので、上記の直線の方程式で表せます。

もちろん平面上の直線の方程式$y = ax + b$に、$x = x_{1},y = y_{1}$を代入したものと
$x = x_{2},y = y_{2}$を代入したものの連立方程式を解く方法でもよいです。

何に対して真っすぐなの？

上記の通り、2点あれば直線ができることがわかりました。

2人がどの位置でキャッチボールしても、本人たちにとっては真っすぐと言えるでしょう。

しかし、それでも彼は「真っすぐになれ」と言ってきます。

すると、彼は「別の基準となる直線に対して真っすぐになれ」という意味で言っている可能性があります。

日本語って難しい。

当時、キャッチボールは本塁方向と三塁方向に分かれて行われていました。
（野球を知らない人はわかりにくくてごめんなさい。）

例えば、「本塁と三塁を結ぶ直線と平行になれ」という表現だと理解できたかもしれません。

いや、理解できても実際にできるかどうかは別です。

なぜなら、人間である以上、多少ずれることは仕方ないからです。

隣の人とぶつからなかったらよくないですか？

遠投もしてたのですが、コントロール悪かったらどうしてもずれますよね？

なぜ真っすぐにこだわるんでしょうか？

真っすぐにするにしても人を動かすんじゃなくて自分が動いたらどうですか？

未だに謎です。

いよいよ「性格的に真っすぐになれ」という意味の可能性が・・・

相方の視点から考える

相方の視点になって考えてみました。

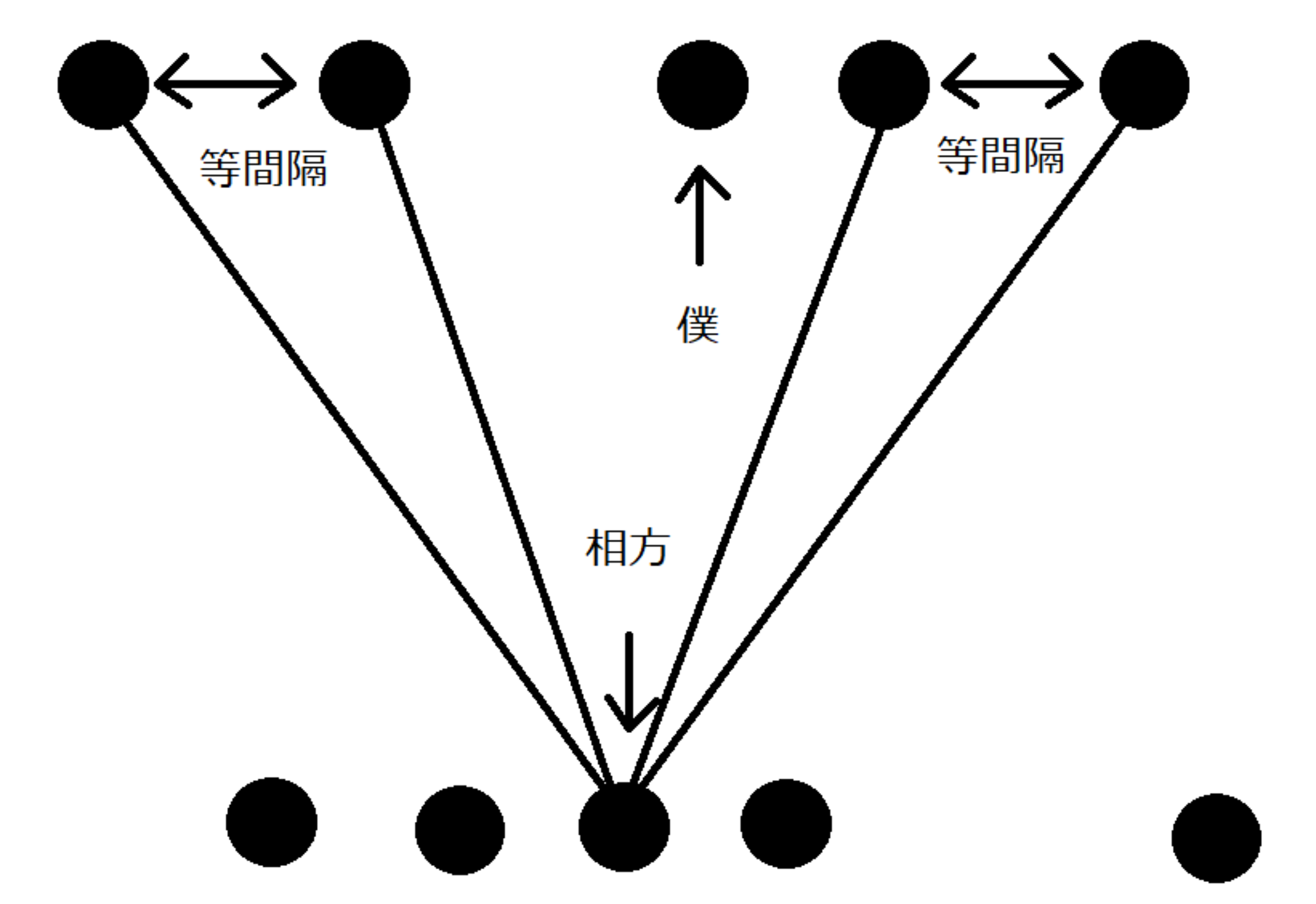これは真っすぐ？

他のメンバーが等間隔で並んでいるのに、僕だけが等間隔でなければ、
相方から見ると確かに「真っすぐでない」ように見えるかもしれません。

自分が動くのではなく、相手を動かして真っすぐにするという意図も分かります。

しかし、この問題での適切な指示は「他のメンバーと等間隔になれ」です。

「真っすぐになれ」では解決しないと思います。

あと、やっぱりコントロールが悪かったらずれます。

まとめ

$$・2点あれば直線ができる。$$
$$・2点を結ぶ直線が「真っすぐ」でない場合、別の基準となる直線が存在する可能性がある。$$
$$・状況を客観視して指示は適切に。$$
$$・ずれてもいいじゃないか　だってにんげんだもの$$
$$・隣の人とぶつからずにキャッチボールができれば、それでいい$$

ちなみに大人になってから、別の人から「もっと素直になれ」と言われたことがあります。

いやいや、素直になるのと人の言うことを鵜呑みにするのとは違うから（笑）