【論理ガール】人生は全て数学で説明できる

先日、数学関連の本を読んだので紹介です。

小説なのですが、「人生は全て数学で説明できる」というテーマで書かれています。

読み終わって思ったのですが、僕と考え方が非常に似ている。

いや、本当に。

これ、僕の記事の方向性と似ている。

勘違いしないでよね！これに影響されて記事を書いてるわけじゃないんだからね！

記事を書いてる途中でこの本を発見しただけなんだからね！

とまあ、僕の話はどうでもいいので、本で出てきた数学の考え方の紹介です！

「人間関係は多いほどいい」は嘘

話の途中で、主人公である論理ガールが、人間関係が多いことが自慢の人に向かってこのように説明しています。

書き方は色々ありますが、全部同じ意味です。
（作中ではシグマが使われていました。ベクトルは僕のオリジナルです。）
$$H=A1・x1+A2・x2+A3・x3+・・・$$
$$　= \sum_{i=0}^{n}A_{i}x_{i}$$
$$　= \begin{pmatrix} A_{1} & A_{2} & ... & A_{n} \end{pmatrix} \begin{pmatrix} x_{1} \\ x_{2} \\ ... \\ x_{n} \\ \end{pmatrix} $$

Hは大きいほど人間関係が充実しているとします。

影響度は、その人が自分にどのくらい影響があるかを表します。
例えば、身近にいる家族や友人はこの度数が大きく、ただの会社の同僚や上司は低い、という風にです。

悪影響を与える人間と過ごす時間が長くなれば、人間関係度数がマイナスになるので、悪影響を与える人間と過ごす時間は短い方がいいですよね。

逆に、いい影響を与える人間と過ごす時間が長いと充実しています。

さらに、時間は限られています。

また、これは小説にはないですが、ダンパー数といって、人間がお互いを認識できる人数は150人くらいと言われています。

ロビン・ダンパー博士が霊長類の大脳のサイズと群れのサイズを測定し、人間に適応したところ150人が限界じゃね？という見解らしいです。

SNSが発展しているとはいえ、濃い関係になりたい人を選んだ方がいいと思います。

友達の少ない僕は「150人は多いだろ！」って思っちゃいますけど、それはおいといて。

まとめると、自分の寿命と、過ごす人数は限られているので、友達は多ければ多いほどよいわけではないということですね。

円の直径から円の面積を求める

円の面積を直感的に捉えるとこうなります。

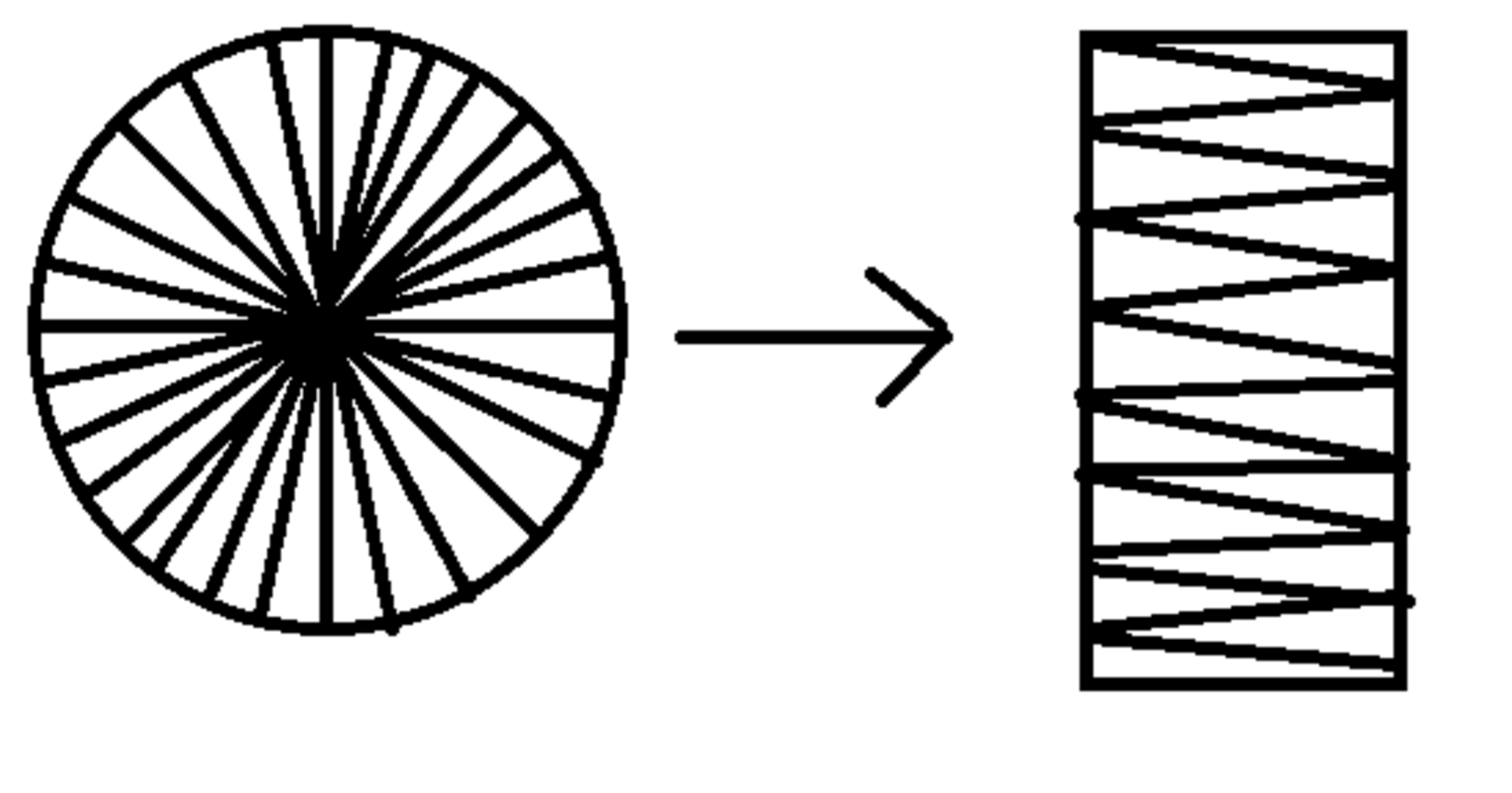円を切ってくっつける

円の半径を$r$とおくと、長方形の面積は

$$横×縦 = r × \frac{直径}{2}$$

直径を$2πr$ということがわかっていれば

$$r × \frac{2πr}{2} = πr^{2}$$

確かに円の面積と一致します。

この説明なら小学生にもわかる気がします。

等差数列、等比数列の考え方

等差数列、等比数列の説明もありました。
例えば

$$1+2+3+...+10=?$$

この程度なら暗算で出ると思いますが、数が大きくなった場合に対応できなくなります。

なので、工夫する必要があります。

例えば

$$1+2+3+...+100=?$$

これは、$100$と$1$で$101$ができます。

これを利用して$S_{n}=1+2+3+...+100$とすると

$$2S_{n}=(1+2+3+...+100) + (100+...+3+2+1)$$
$$= 101+101+...+101=101×100=10100$$
$$S_{n}=5050$$

これなら小学生でも解けますよね。ガウスじゃなくても。

初項$a_{1}$公差$d$の等差数列の和$S_{n}$は

$$2S_{n}= \lbrace a_{1}+(a_{1}+d)+(a_{1}+2d)+...+(a_{1}+(n-1)d) \rbrace$$
$$　　 + \lbrace (a_{1}+(n-1)d)+...+(a_{1}+2d)+(a_{1}+d)+a_{1} \rbrace$$
$$=2na_{1}+n(n-1)d$$
$$S_{n}=na_{1} + \frac{n(n-1)}{2}d$$

ということがわかります。

また、初項$a_{0}$公比$r$の等比数列は

$$S_{n} = a_{0} + r・a_{0} + r^{2}・a_{0}+...+r^{n}・a_{0}$$

これに$r$をかけてずらします。

$$rS_{n} =　　 r・a_{0} + r^{2}・a_{0}+...+r^{n}・a_{0} + r^{n+1}・a_{0}$$

差をとると

$$(1-r)S_{n} = a_{0} - r^{n+1}a_{0} = (1-r^{n+1})a_{0}$$
$$S_{n}= \frac{(1-r^{n+1})}{1-r}a_{0}$$

これが等比数列の公式です。

公式じゃなくて考え方を覚えてください。

まとめ

他にもいろいろな考えを数学で考えるということをしているのですが、続きは書籍を読んでみて下さい。

数学初心者にもスッと読めると思います。