難角問題の新手法(連立法)

　こんにちは、simasimaです。
　今回は難角問題を半分くらい倒せる新たな手法、連立法を思いついたので紹介しようと思います。

手法

　手法はいたってシンプルです。(私の前に誰か思いついてそう...)

1. 与えられている角を $x,y,...$ という風に文字で置く。すると答えの角は実数 $p,q,r...$を用いて $px+qy+r$ のように表される。(事が多い。)
2. 問題の与えられた角以外の条件を満たすような極端な図を書き、$x,y,...$ と答えの角を求める。すると$ap+bq+r=c$ といった形の式が立つ。
3. 2を繰り返すと、$p,q,r...$ についての連立方程式が作れるので、これを解いて、$p,q,r,...$を求める。
4. 与えられている角を $px+qy+r$ に代入するとそれが答え。(の事が多い。)

　この方法は与えられている角度が全て $12$ や $20$ の倍数の時は使えない事が多いですが、逆にそれ以外の時はかなり使えます。

実際に使ってみよう

　今回はJMO2023予選の問10を解いていきます。JMO予選は答えのみなので本番でもこの手法が使えますね。

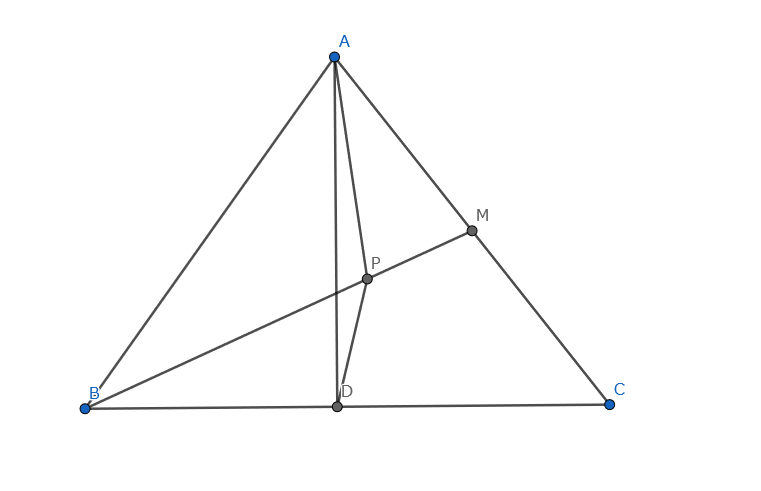
与えられている角がある程度汚いので、連立法が使えそうです。
$\angle BAP=x^{\circ }$$\angle PDB=y^{\circ }$とおきます。
$\angle BAC$は、$x,y$の値によらず、実数$p,q,r$を用いて$(px+qy+r)^{\circ }$の形で表せます。(多分)
$p,q,r$の値を求めに行きましょう。

まず、三角形$ABC$を勝手に正三角形にしてみます。
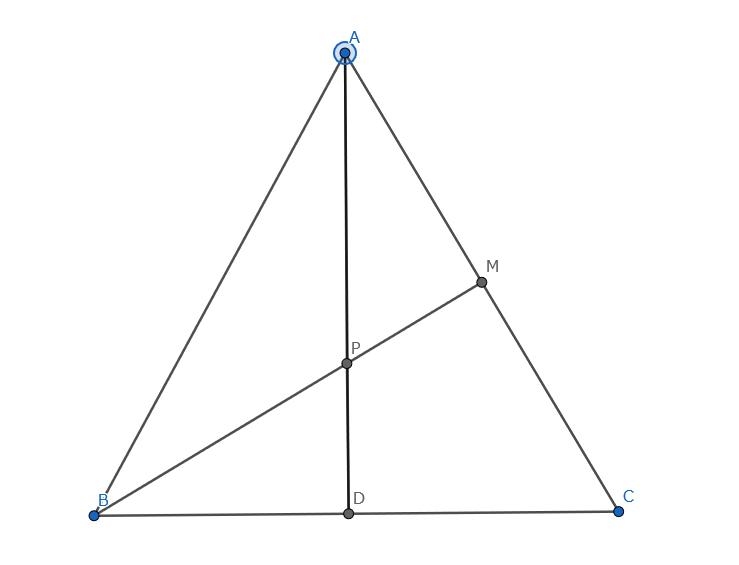作図適当なの許して
この時$BM$が垂線になり、いろいろ扱いやすくなりました。
この時、$\angle BAP=30^{\circ }$$\angle PDB=90^{\circ }$$\angle BAC=60^{\circ }$なので、次の式が成り立ちます。

$AB=BC$ の場合をもう一つ考えてみましょう。$\angle ABC=40^{\circ }$とします。

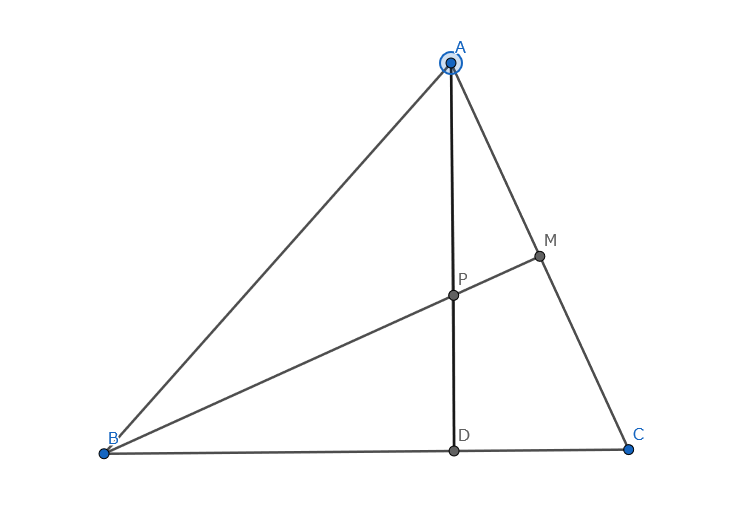
この時、$\angle BAP=50^{\circ }$$\angle PDB=90^{\circ }$$\angle BAC=70^{\circ }$なので、次の式が成り立ちます。

$AB=BC$ の場合をこれ以上考えても$90q+r$の部分が分からないので別の図を考えます。
$P$をいい位置に持って行くために三角形$BAM$を直角二等辺三角形にしてみます。

この時、$4$点$A,P,B,D$が明らかに共円です。
この時、$\angle BAP=45^{\circ }$$\angle PDB=135^{\circ }$$\angle BAC=90^{\circ }$なので、次の式が成り立ちます。

さて、$3$つの式が立ったので$p,q,r$を求めてみましょう。

$p=\frac{1}{2},q=\frac{1}{2},r=0$と求まりました。
後は問題の数値を入れるだけです。$\frac{1}{2}\times 41^{\circ }+\frac{1}{2}\times 115^{\circ }+0=78^{\circ }$
これは正解の値です。
なんとJMO予選の10番を本質部分に何も触れずに解くことが出来てしまいました。

応用

この問題では与えられた角度が$41^{\circ },115^{\circ }$と、どちらも汚い値でしたが、他の問題で、例えば与えられた角度が$60^{\circ },115^{\circ }$だったらどうすれば良いでしょうか。この場合は$60^{\circ }$は残して、$115^{\circ }$を文字で置くと多分上手くいきます。また、が$57^{\circ },63^{\circ }$だったらどうでしょうか。これは、$57^{\circ }+63^{\circ }=120^{\circ }$が見えるので、$x,120-x$という風に置けば良いです。

この手法はこの問題以外にも沢山の問題で通用することをすでに確認しています。この記事が伸びたら他の問題を解いてみる応用編を書くかもしれないので、書いて欲しいと思った人はこの記事に高評価とかもろもろをお願いします。なんなら、連立法を使ってこの問題解いてみた！みたいな記事を私以外の人間が書いてくれると嬉しいです。(他力本願)