錐の体積で使う「1/3」の意味、わかりますか？

小学校で習うこと

小学校の時点では、実際に直方体と正四角錘、円柱と円錐、三角柱と三角錐などの容器に水を使って
「ほら、四角錘から直方体に水を入れると1/3だよー」と見せられると思います。
（平成10年くらいの学習指導要領の内容ですが、僕の教科書ではそうなってました。）

しかし、よくよく考えると「1/3ってどこから出るんだ？」と思いました。
今回は、この1/3がどこから出てくるのかを紹介します。

円錐の体積

結論から言うと、積分を使います。
（積分を理解している前提で話します。）

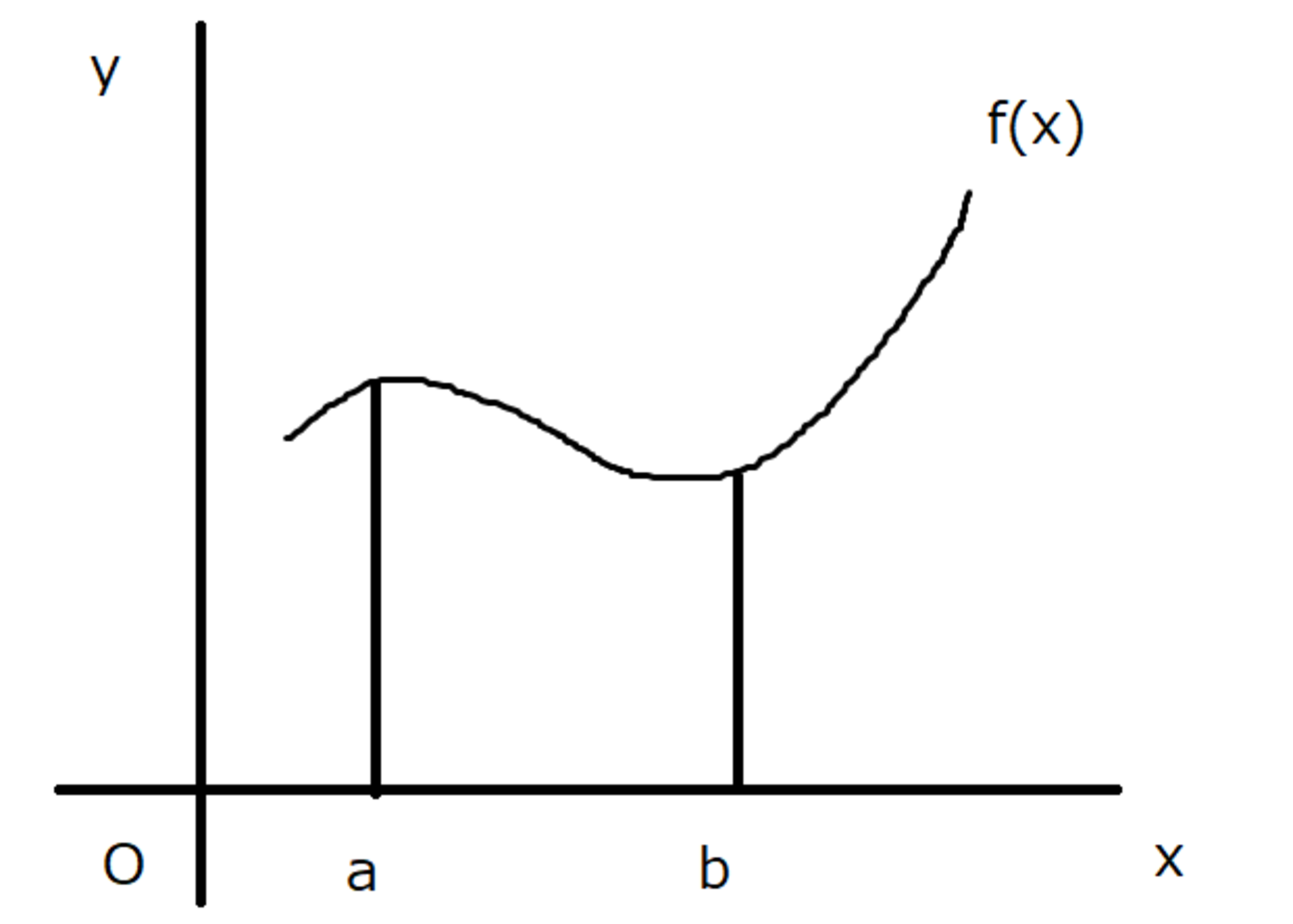回転体の体積

例えば、上記の図において、$[a,b]$での$f(x)$の回転体の体積は分かると思います。

半径$f(x)$の円が、$[a,b]$を連続的に移動していくというイメージです。

円の面積は$半径^2×π$なので、半径を$f(x)$とすると、円の面積は$πf(x)^2$となります。

これが$[a,b]$で連続的に移動します。

ここで、錐の場合はこうなります。

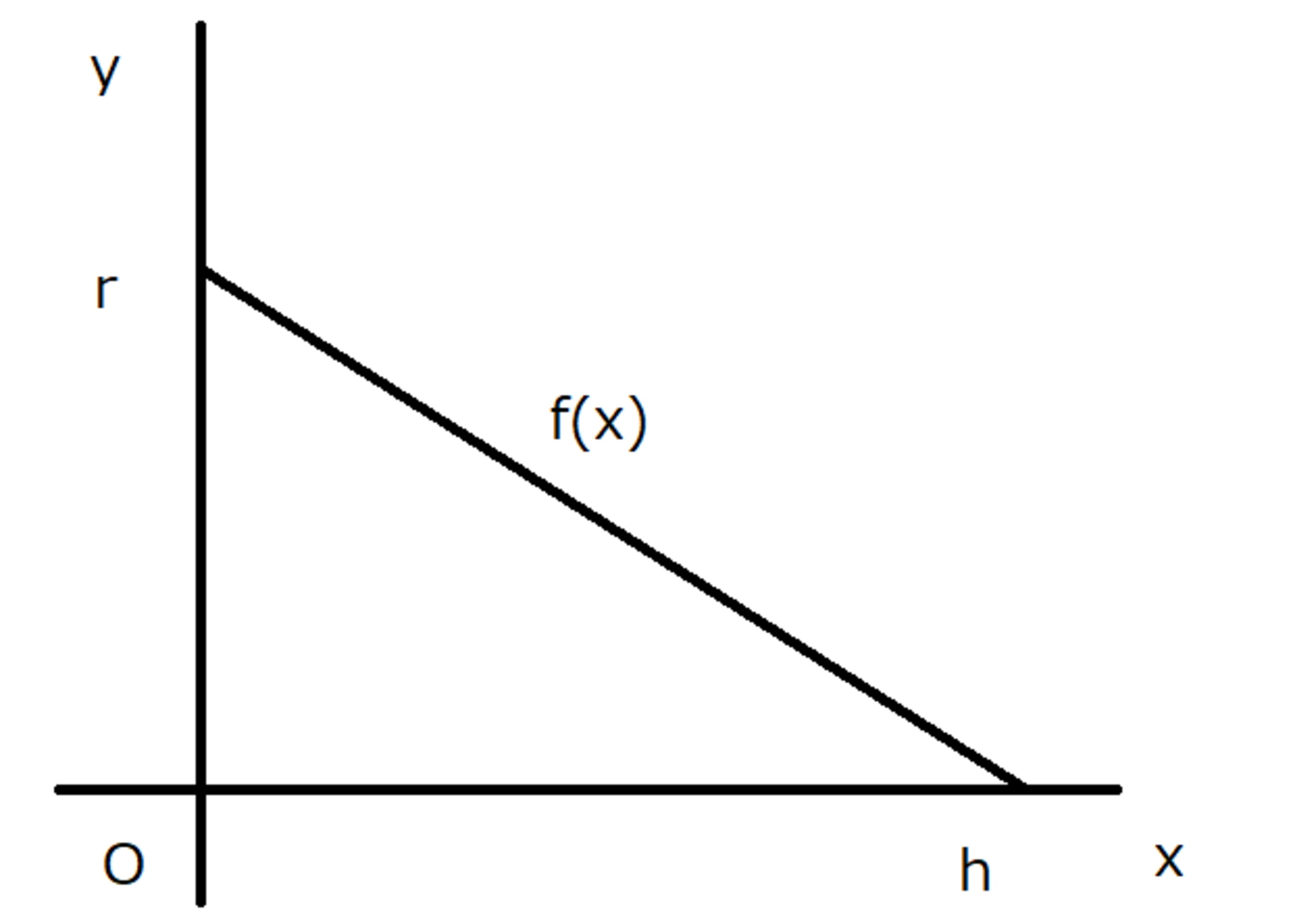錐の積分

底辺をr、高さをhとします。

このとき、$f(x)= -\frac{r}{h}x + r$となります。

よって

円錐の体積 =
$$ \int_{a}^{b} πf(x)^2 dx$$
$$= π \int_{0}^{h}(-\frac{r}{h}x + r)^2 dx$$

$t=-\frac{r}{h}x + r$とすると
$$\frac{dt}{dx} = -\frac{r}{h}$$
$$dx = -\frac{h}{r}dt$$
$$[0,h]→[r,0]$$

円錐の体積 =
$$π \int_{r}^{0}-\frac{h}{r}t^2dt$$
$$= -π\frac{h}{r} \int_{r}^{0}t^2dt$$
$$= -π\frac{h}{r} [\frac{1}{3}t^3]_r^0$$
$$= -π\frac{h}{r} (- \frac{1}{3}r^3)$$
$$= \frac{1}{3}πr^2h$$

ということで、めでたく$\frac{1}{3}$が出てきました。

しかし、これは円錐の場合です。

四角錘、三角錐でも使えるようにするにはどうすればよいかを考えます。

四角錘、三角錐など、あらゆる錐の場合

まず、底面積$S(x)$に対し、$x \in [0,h]$を考えます。

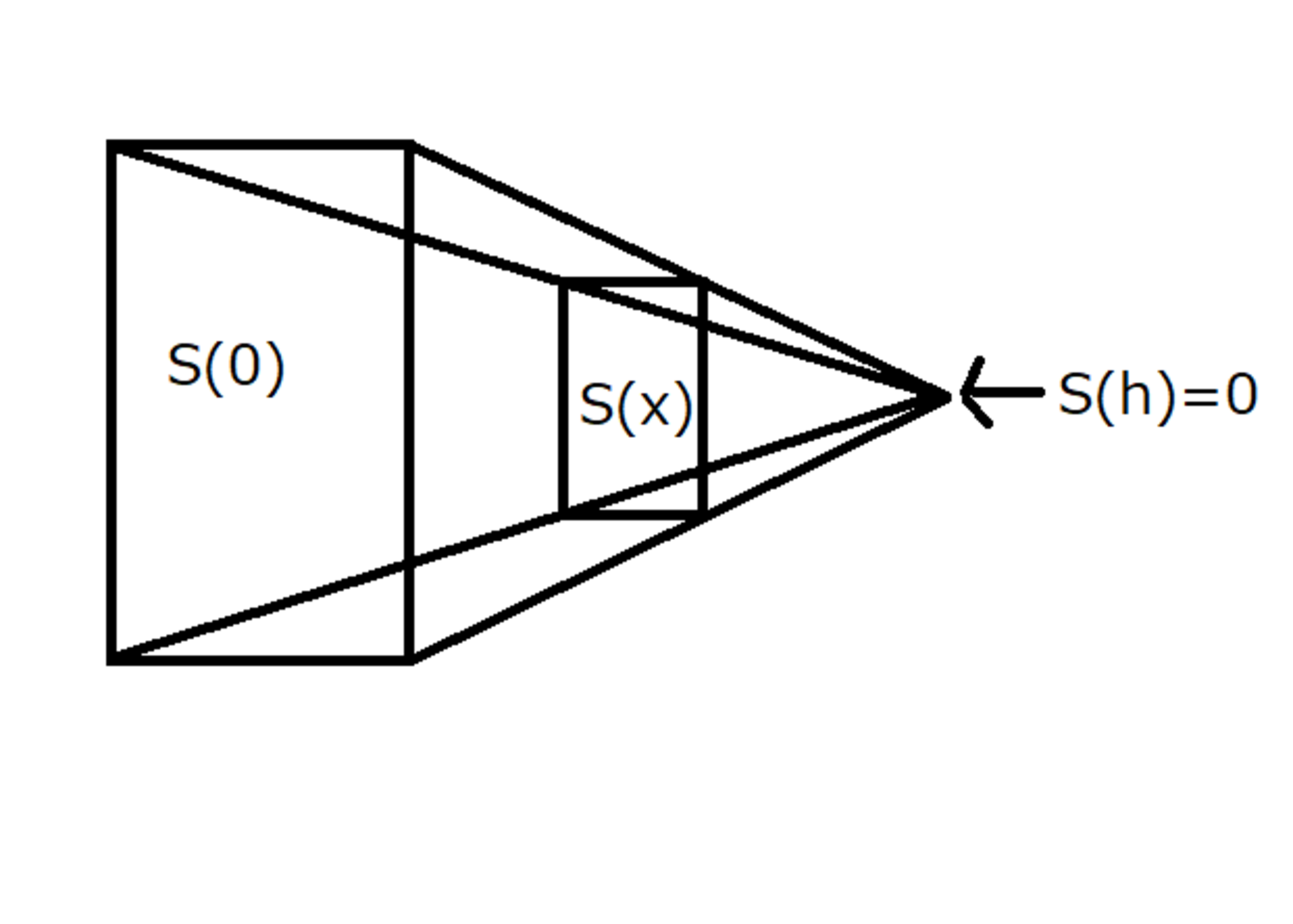底面積S(x)

錐の側面は直線でできているので、$S(x)$は一次関数です。

よって、$S(x) = ax+b$とかけます。

また、$S(h) = 0$なので、$a=-\frac{b}{h}$

つまり、$S(x) = -\frac{b}{h}x+b$

$t = S(x)$とすると
$$\frac{dt}{dx} = S(x)' = -\frac{b}{h}$$
$$dx = -\frac{h}{b}dt$$
$$[0,h]→[b,0]$$

よって、

錐の体積

$$= \int_{0}^{h} S(x) dx$$
$$= \int_{b}^{0} -\frac{h}{b}tdt$$
$$= -\frac{h}{b}\int_{b}^{0} tdt$$
$$= -\frac{h}{b}[\frac{1}{2}t^2]_b^0$$
$$= \frac{1}{2}bh$$

あれ？

どこを間違えたんだ・・・？

多分ここですね →　錐の側面は直線でできているので、$S(x)$は一次関数です。

$S(x)$を二次関数としましょう。

$S(x)=0$となるのは、$x=h$のときだけなので
$$S(x)=a(x-h)^2$$

$t=x-h$とすると
$$\frac{dt}{dx} = 1$$
$$dx = dt$$
$$[0,h]→[-h,0]$$

よって

錐の体積（今度こそ）

$$= \int_{0}^{h} S(x) dx$$
$$= \int_{0}^{h} a(x-h)^2 dx$$
$$= a\int_{-h}^{0} t^2 dt$$
$$= a[\frac{1}{3}t^3]_{-h}^{0}$$
$$= \frac{1}{3}ah^3$$

底面積をSとすると$S(0)=ah^2=S$

$$a=\frac{S}{h^2}$$

$$すなわち$$

$$錐の体積 = \frac{1}{3}Sh$$

やったあ！

なぜ間違えたか

最初に間違えた$\frac{1}{2}bh$が表しているのは、「底面積×高さ÷2」で、立体を半分に切った形をしています。

どうしてこうなるかというと、錐にするには面を縮小しなければならないのですが、辺しか縮小していなかったのです。

図で表すとこうです。

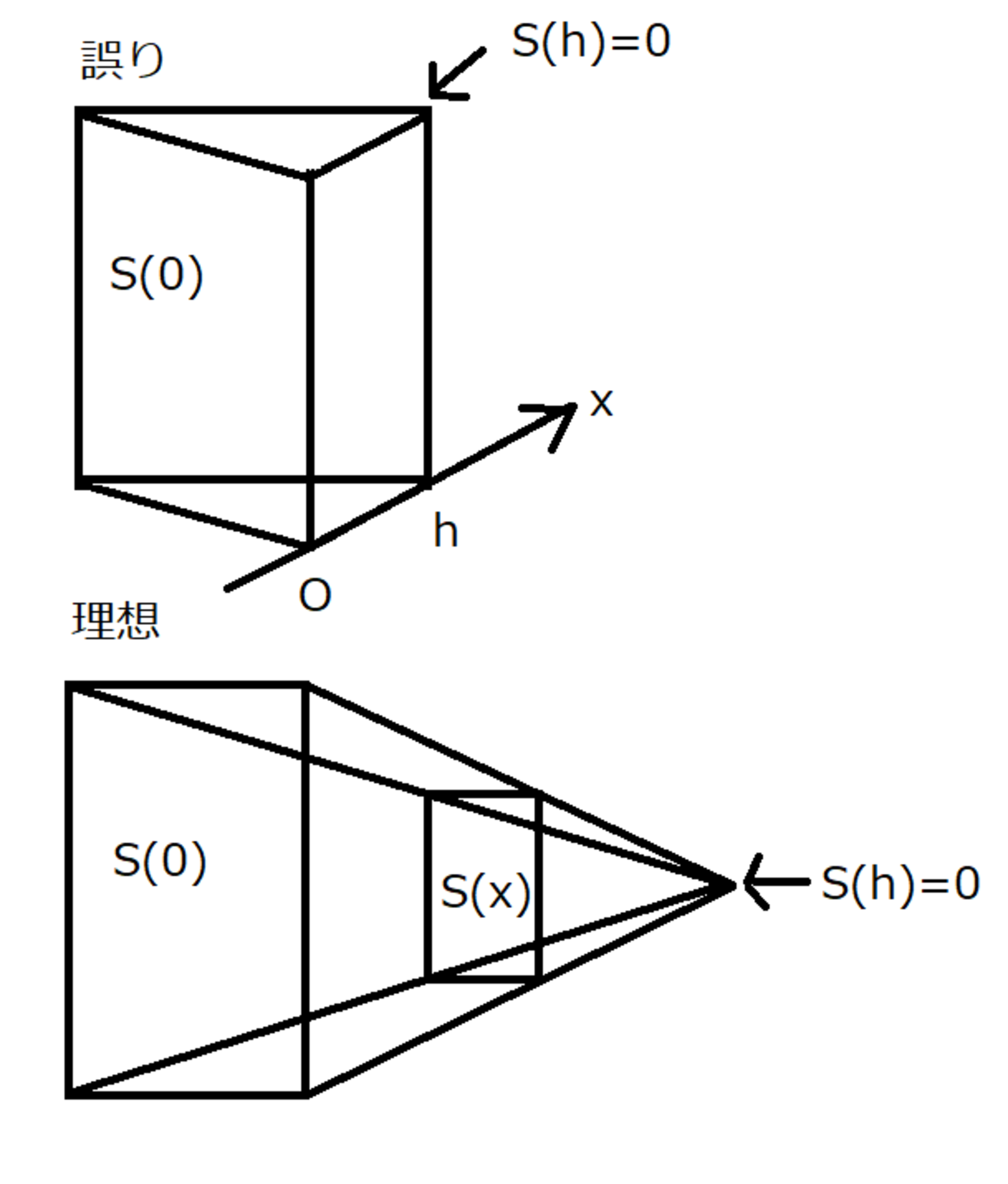柱と錐

$S(x)$を一次関数にしてしまうと、上の図のようになります。

$y$座標しか減少していません。

本来は、下の図のように、減少しなければなりません。

$y$座標と$z座標$が減少しています。

一辺を$n$倍すると、面積は$n^2$倍になります。

なので、$S(x)$は二次関数です。

まとめ

$$・錐の\frac{1}{3}は積分によるもの$$
$$・錐の底面積は、頂点に向かって二次関数的に減少する$$