チコちゃんが叱られる！？〜「円周率がずっと続くのはなぜ？」における決定的誤謬〜

2021年7月2日放送の「チコちゃんに叱られる！」(NHK総合)にて「円周率がずっと続くのはなぜ？」という疑問が投げかけられました．そして，番組内でのチコちゃんの回答は

「円の長さを正確に測るのは，本当に無理だから」

というものでした．これをめぐり，SNSを中心に数学界隈から批判が集まっています．本記事では，チコちゃんの回答のどこに誤解があるのか，はじめにその急所を突きます．追って，実際に放送された議論の欠陥も指摘することにしましょう．

さて，では一番の問題点はなんなのでしょうか．それはズバリ，

数学定数と物理定数の違いを理解していないこと

に尽きると考えています．数学定数とは基本的に実数や複素数の要素であって，今回の話題である円周率$\pi$をはじめ黄金数$\phi(=\frac{1+\sqrt{5}}{2})$や自然対数の底$e$などがあります．一方で物理定数とは物理量であって，真空中の光速$c$や万有引力定数$G$，ボーア半径$a_0$などがあります．

まず物理定数というのは物理的な実験で計測される量であり，当然ながら装置の精度によって誤差が生じます．真空中の光速は速さや長さの基準として使うために定義値として人為的に誤差なく定められていますが，これも数学的に定義される後述の数学定数とは根本的に異なるものです．一般に真の値は誰にもわからないものだということです．勝手に我々が定数だと思っているだけで，そもそも一定の値をとるのかも不明です．チコちゃんがした説明は，こちらの概念に立脚したものだと言えるでしょう．

対する数学定数は，数学的に定義され，一意的に存在が保証されている数です．例えば$\sqrt{2}$は「$2$乗すると$2$となる正の実数」という定義があるわけで，中間値の定理から実数の要素としてただ一つ存在することが示せます．確かに，$N$があるとてつもなく大きな自然数だとすると，小数第$N$位がなんであるか，人類の誰も計算してみたことはないでしょう．しかし，この場合は物理定数のそれとは全く異質なものであることに注意しなくてはなりません．皆さんもやろうと思えば紙上の計算で$\sqrt{2}$の小数第$10$位に並ぶ数字を確信をもって求めることができるのです．

ここで円周率の定義を振り返ってみましょう．円とは平面上で定点からの距離が一定の点の集合のことでした．全ての円は相似ですから，直径の長さに円周の長さは比例します．この比例定数のことを円周率とよんでいます．また，円周をはじめとする曲線の長さは積分の言葉で厳密には定義されるので，定積分を用いて

$$\pi=4\int_{0}^{1}\sqrt{1-x^2}dx$$

などと定義しても構いません．循環論法には注意が必要ですが，他にも同値な定義はたくさん考えられます．いずれにしても，数学的に定義された数学定数であることは明らかです．したがってチコちゃんの「正確に測るのは無理」というのは不適切だということです．これには諸説ないです．

ここで放送中の議論を振り返ります．大まかには，円に内接する正多角形と外接する正多角形の周長で両側から円周の長さを評価すると円周率の近似値が求まるが正多角形の頂点の個数を増やしていっても永遠に評価は終わらないというものでした．円周率はその値を有限な十進法表示でバシッと与えることができないのは事実です．しかしそれは，測定が終わらないからではなく，無理数だからです．だいたい，円周長の評価に用いている正多角形の周長だってそのほとんどが有限な十進法表示をもたないではないですか．

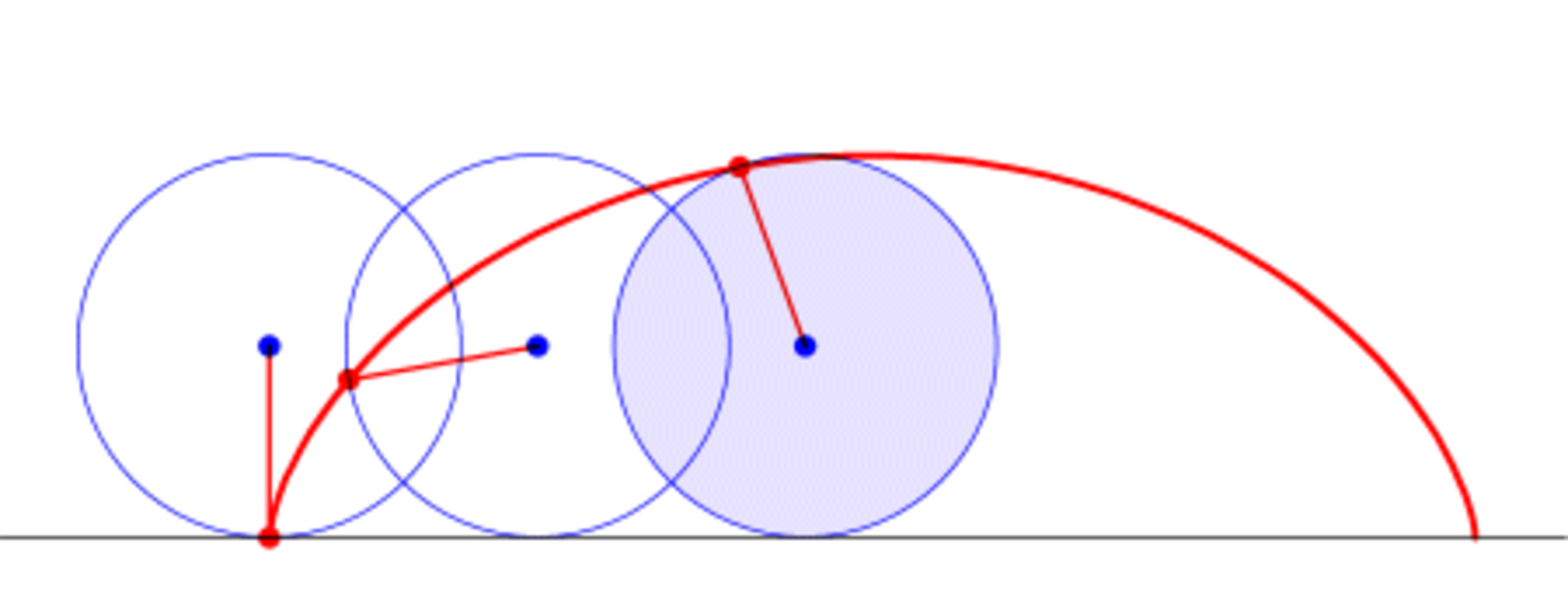
そのような評価が終わらなくても，真の値がすっきりした数になることもあります．サイクロイドを例として挙げましょう．ある定直線上を円が滑らずに転がるとき，その円周上の一点が描く軌跡をサイクロイドといいます．特に円がちょうど一周したとき円周上の一点が動くのは以下のようなサイクロイド曲線の一部となりますが，この長さは円の半径を$1$としたときちょうど$8$になることが知られています．折れ線で近似する方法では測定が終わりませんが，数学では極限計算が行えますから，真の値を得ることができます．数学のことを「有効数字$\infty$桁の自然科学」と呼んだら専門家からは叱られてしまうかもしれませんが，筆者はそうした印象を持っています．

そして，肝心の円周率が無理数であることを証明するのは微積分を用いずには困難です．正直に言って題材選びがよくなかったと言わざるを得ません．証明ではなく説明をするにしても，無限大について正しい感覚がなければ理解できないと思います．現実的には「$\sqrt{2}$がずっと続くのはなぜ？」くらいに留めておかないと適切な内容にはならないでしょう．

急ピッチで書きあげましたが，数学に興味を持った皆さんの真摯な心に届きますように．