【角度不要説】ラジアンでよくない?
あなたは$1$周は$360°$ということをご存じかと思います。
なぜ360°という中途半端な数なのでしょうか?
(数学ガチ勢の方は美しいと思うかもしれませんが、一般の人目線で考えると中途半端だと思います。)
また、数学で円を扱う場合は、角度ではなく弧度(ラジアン)を使います。
じゃあ義務教育で習った角度はなんだったんだよ!ともなるわけです。
今回は、それらの疑問にお答えします。
ラジアンとは
簡単に言うと$1$周を$2π$としたときの、ある扇形の弧の大きさがラジアンとなります。
例えば、弧の長さが$1$の扇形の角度は$1$ラジアン、弧の長さが$\frac{π}{2}$の扇形の角度は$\frac{π}{2}$ラジアンとなります。
このラジアンで計算すると、計算が楽なのです。
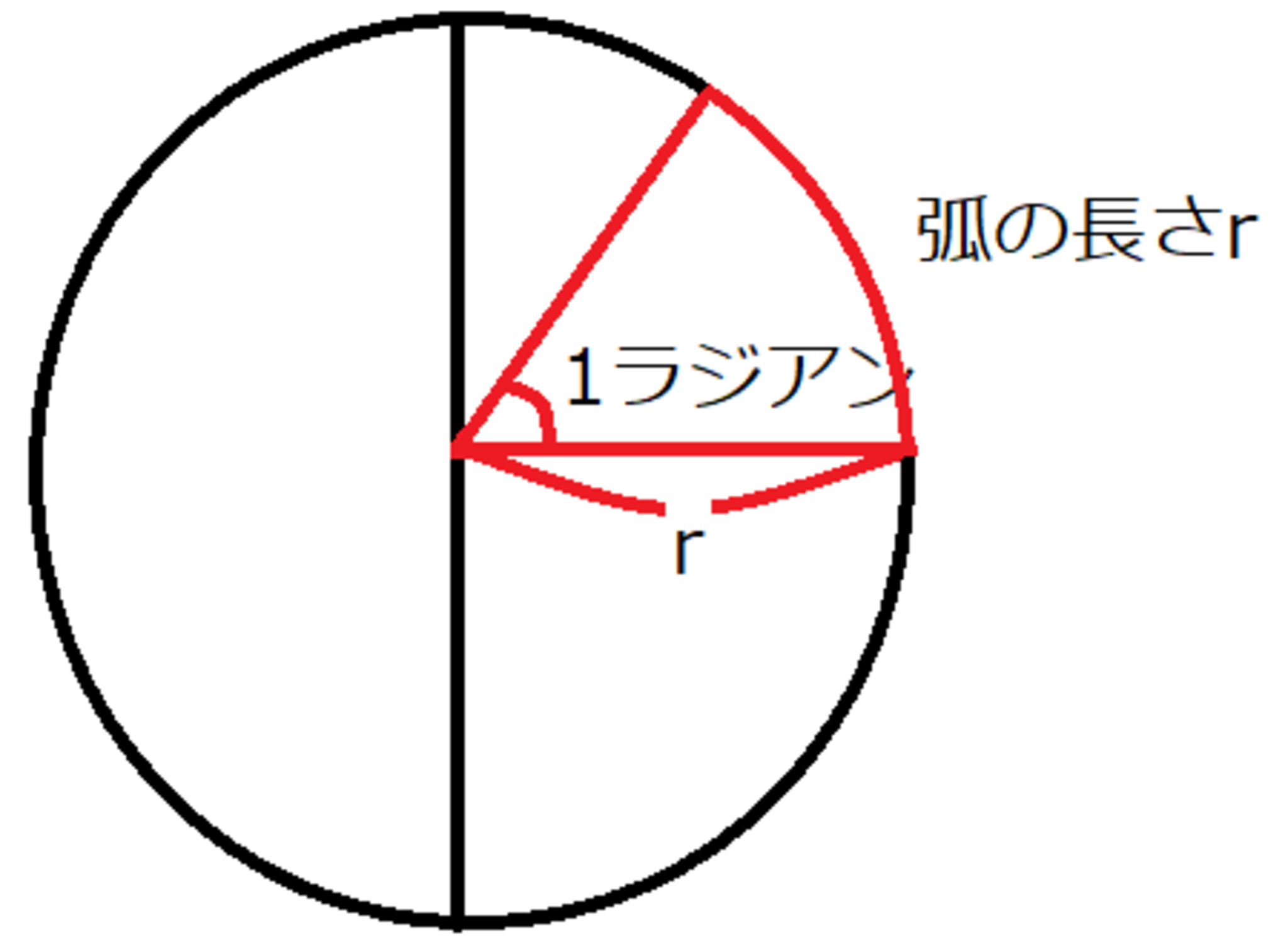 ラジアン
ラジアン
例えば、半径rの円を$45°$だけ切り取った扇形の弧の長さ、面積を求めるとしましょう。
角度で計算
$$弧の長さ = 直径 × π × \frac{角度}{360°}$$
$$ = 2πr × \frac{45°}{360°}$$
$$ = 2πr × \frac{1}{8}$$
$$ = \frac{π}{4}r$$
$$面積 = 半径 × 半径 × π × \frac{角度}{360°}$$
$$ = r × r × π × \frac{45°}{360°}$$
$$ = πr^2 × \frac{1}{8}$$
$$ = \frac{π}{8}r^2$$
ラジアンで計算
$45°$は$\frac{1}{8}$周なので、弧度に直すと$2π × \frac{1}{8} = \frac{π}{4}$ラジアンです。
$$弧の長さ = 半径 × ラジアン$$
$$ = r × \frac{π}{4}$$
$$ = \frac{π}{4}r$$
$$面積 = 半径 × 半径 × ラジアン$$
$$ = r × r × \frac{π}{8}$$
$$ = \frac{π}{8}r^2$$
角度の場合は、いちいち$360$で割る必要がありますが、最初からラジアンが分かっている場合は、$360$で割る必要はないので、計算の負担が少ないです。
面積の求め方の別解(余談)
ちなみに弧の長さが分かっていれば、$「\frac{弧の長さ}{2}×半径」$でも求まります。
これは、扇形を細かく分割し、うまく組み合わせて
$縦×横= \frac{弧の長さ}{2}×半径$の長方形にするわけです。
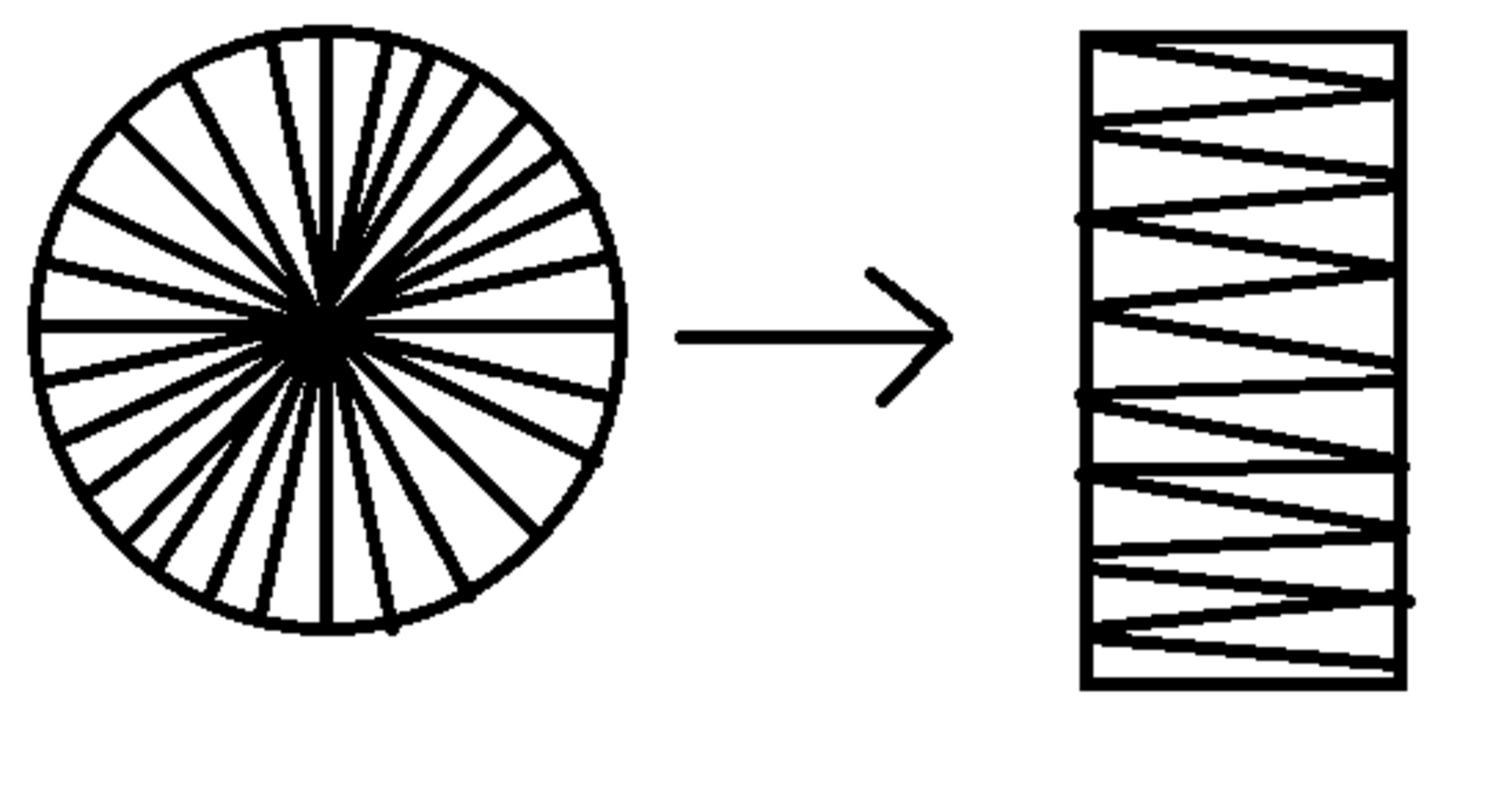 円の面積を求める場合のイメージ
円の面積を求める場合のイメージ
また、扇形を$n$等分し、底辺=$\frac{弧の長さ}{n}$、高さ=$半径$の小さい三角形が$n$個あるとみなせば、
$(底辺×高さ÷2)×n = (\frac{弧の長さ}{n} × 半径 ÷ 2) × n$
$= 弧の長さ × 半径 ÷ 2$
となり、弧の長さを底辺、半径を高さとする三角形とみなせるわけです。
長方形パターンと三角形パターンは、お好みでどうぞ。
角度の存在意義
「じゃあ角度は廃止したらよくない?」という方は、ちょっと待ってください。
数学ではラジアンは大きな意味を持ちますが、天文学や地理などではラジアンよりも角度の方が便利です。
そもそも角度と言うのは、最初は実生活で使っていたのですよ。
古代エジプトなんかを想像すると分かりやすいかもしれません。
まだピラミッドを作っている時代で、ピタゴラス、アルキメデスなどの数学者が登場する頃よりも前で、数学はあまり発展していない時代です。
すると、その人たちにとって身近な数学というのは天体を利用した暦となるわけです。
例えば、星を使った暦の計算です。
$1年 = 365日$です。
また、$1年$というのは、地球から見える星が、$1$周して元の位置に戻るまでの時間です。
さらに$365$よりも、$360$の方が約数が多く、分割がしやすいので
$1周 = 360°$となるわけです。
$360 = 2^3 × 3^2 × 5$なので、$4×3×2 = 24$個となります。
$360$の約数
$1,2,3,4,5,6,8,9,10,12,15,18,20,24,30,36,40,45,60,72,90,120,180,360$
地球も球体で、$1$周が$360°$であるため、緯度、経度にも度数法が使われています。
もし緯度、経度が弧度で「東経$\frac{64}{135}π$!」とか言われてもピンときませんもんね。
ちなみに偶然ですが、日本を$東経135°、$北緯45°とすると、
弧度はそれぞれ$\frac{3}{4}π,\frac{1}{4}π$というきりのいい数字になります。
(ただし、北緯$45°$は択捉島で、最北端となります。)
軍隊で使うのはラジアン
こちらはミルという単位が使われており、語源はミリラジアンです。
丁度$1$km先にある$1$mの物体を見る角度が$1$ミルです。
これは、角度$θ$が小さい場合に$sinθ ≒ θ$という特徴を利用しています。
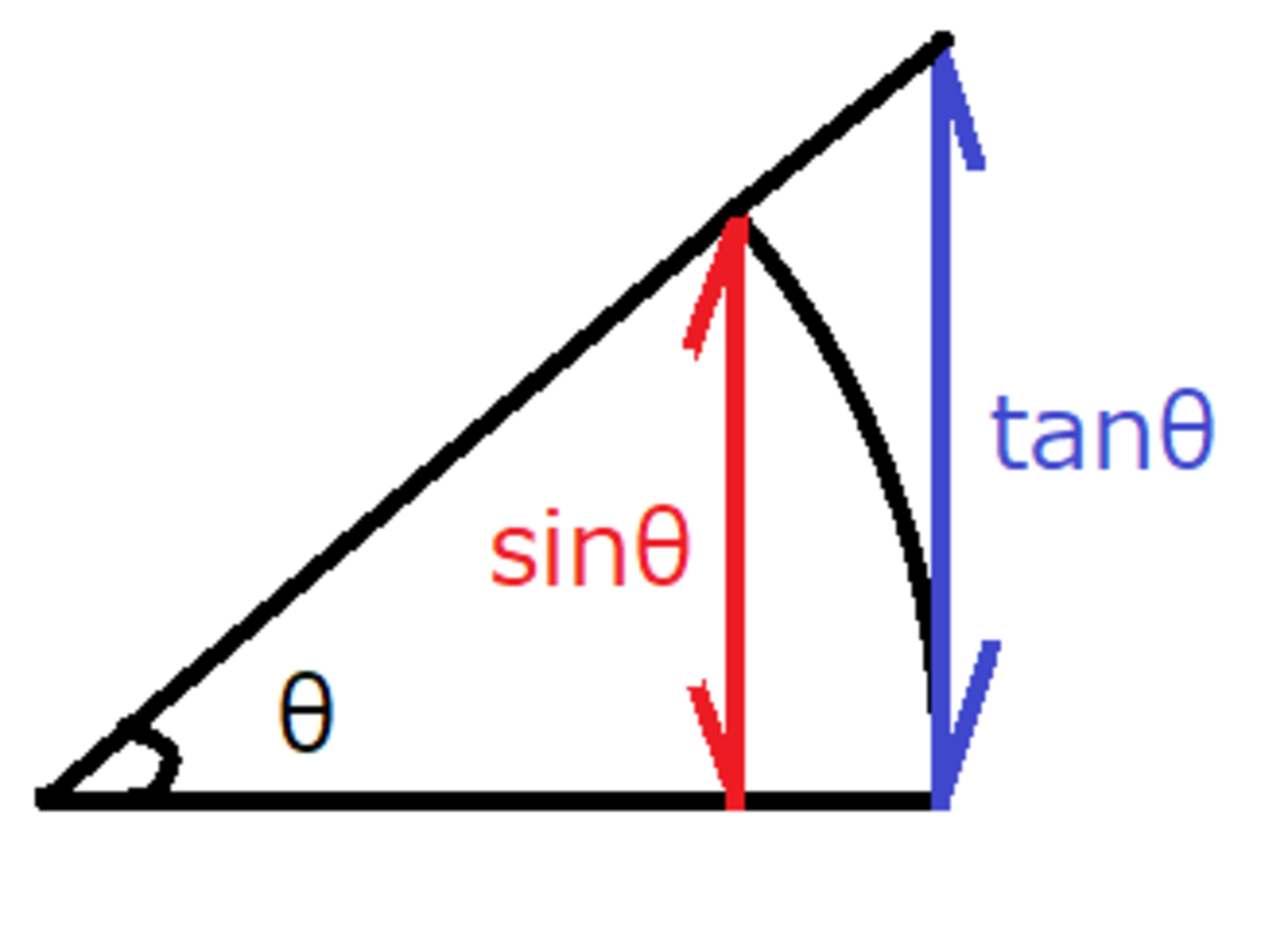 sinθ ≒ θ
sinθ ≒ θ
半径$1$の単位円に対し、角度$θ$の扇形を描きます。
弧の長さは$θ$なので、図から$sinθ < θ < tanθ$となります。
$sinθ < θ$より、両辺$θ$で割ると
$\frac{sinθ}{θ} < 1 -①$
$θ < tanθ$より、両辺$\frac{cosθ}{θ}$をかけると
$cosθ < \frac{sinθ}{θ} -② (∵tanθ = \frac{sinθ}{cosθ})$
①、②から
$cosθ < \frac{sinθ}{θ} < 1$
$ \lim_{θ \to 0} cosθ = 1$なので
$ \lim_{θ \to 0} \frac{sinθ}{θ} = 1$
ここで、弧の半径を$1km$とすると、$sinθ = 0.001km$のとき$θ ≒ sinθ = 0.001$となり、$1km$先の人を銃でしとめるのに都合がいい角度だと考えられます。
ちなみに、よく坂道で使われる単位で、千分率パーミルにもミルという単語がついています。
高さと距離が$\frac{1}{1000}$となる角度が$1$パーミルですね。
不採用となったグラード
調べたら面白かったので紹介します。
ある地域ではグラードという単位が使われていたそうです。
北を$0$グラード、時計回りに値が大きくなっていきます。
$1$周$400$グラードとし、例えば現在の向きが$131$グラードとしたら、左を向くと$31$グラード、右を向くと$231$グラードと、$100$の位を変えるだけでよいという単位が作られたそうです。
ただ、この単位はローカルすぎますし、$400$よりも$360$の方が約数が多いので、採用されなかったそうです。
まとめ
・ラジアンは計算しやすい
・角度は実生活、特に地理、天文の分野などで役に立つ
・不要な単位は採用されない
雑談
不要な単位で思い出したのですが、畳とか合とかポンドとかヤードとかも数学では不要だと思ったのですが、実生活では役に立っているそうです。
例えば、$3合 = 1ポンド$で、$1$人の$1$日分の食事量となるそうです。
また、起きて半畳寝て一畳というように、人の大きさが畳で表されたり、感覚が掴みやすいようです。
ただ、人を基準にした単位は指標にはなると思いますが、正確さに欠けるとは思うので、感覚と正確さのどちらを優先させるかで使い分けたらよいと思います。
とはいえ、今寸とか尺とか使う人いるのか?
一寸法師とか尺八とかシャクトリムシくらいだよな。
