【公式を覚えない数学】みはじ

あらすじ

「みはじ(きはじ)」とは、道のり(距離)、速さ、時間をまとめた総称、あるいはそれらを求める計算方法のことである。

既に根絶されたと考えられるが、今もなお目撃情報が相次いでいるという。

「みはじ」を植え付けられた子供たちは大人になった後にまで影響が及び、次第に体を蝕んでいくという。

そして、「みはじ」に汚染された大人はまた子供たちに「みはじ」の大切さを伝え、子供たちは「みはじ」に汚染されるという。

数学者たちはこの悪循環をいち早く察知し、解決に臨んでいるが、この危険性を誰も理解してくれないという。

「みはじ」の悪いところ

以上が茶番でした。

最初の『「みはじ(きはじ)」とは・・・』の文以外全部嘘です。

「～という」の部分は誰が言っているのかとのことですが、全部僕が言い張ってるだけなので安心してください。

「みはじ」は以下のような算出方法です。

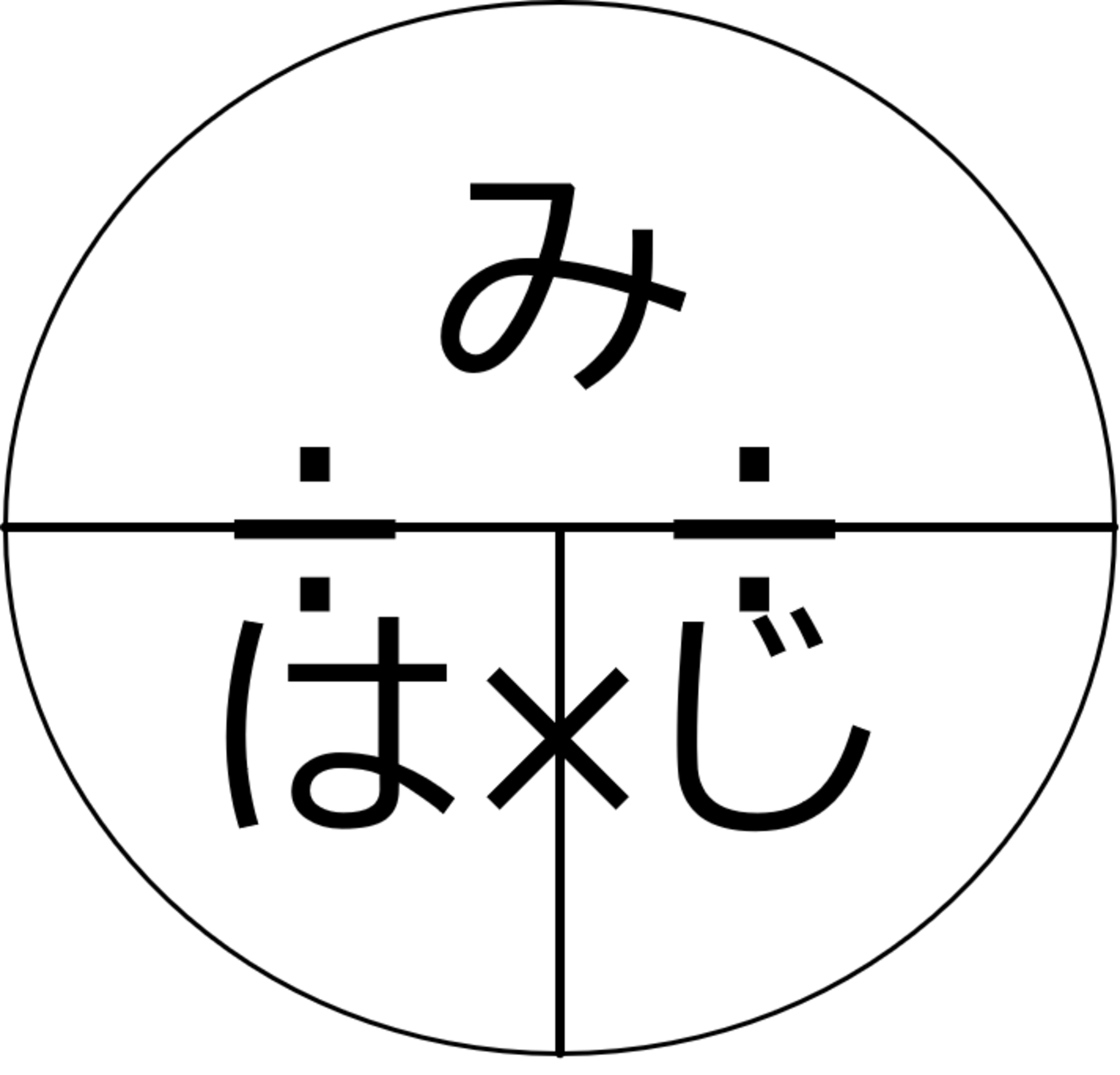みはじ

1. まず円を描き、Tを描きます。
2. 「み」をTの上に置き、「は」を左下(右下)、「じ」を右下(左下)に置けば図は完成です。
3. 後は求めるものを隠せば、計算式が思い出せるわけです。
   例えば、「み」を隠すと、「は」×「じ」つまり「速さ」×「時間」で求まります。
   「は」を隠すと、「み」を分子、「じ」を分母に見立てて、「道のり」÷「時間」で出てくるわけです。

しかし、この図を見るたびにこう思います。

「えーマジみはじ！？キモーイ！」

「みはじが許されるのは小学生までだよね」

以下、理由と対策を挙げます。

公式は作るもの

「みはじ」は一見便利な公式に見えますが、こう言う人が時々います。

「あれ？速さってどうやって求めるんだっけ？」

全然覚えられてねーじゃねーか！

それもそのはずです。

あの図だけでは、道のり、速さ、時間の関係の本質は見えないからです。

「公式は覚えるもの」と考えると当然忘れます。

そもそも公式を忘れるということ自体おかしな話です。

なぜかというと公式は作れるからです。

何言ってんだこいつと言われるかもしれませんが、「みはじ」を例に公式を作っていきましょう。

長さの定義

まず、長さを定義しましょう。

2021年現在では1mは以下のように定義されています。

この$299792458$という数字がどこからきたのか謎ですけども。

これが長さの定義です。

時間の定義

次に、時間を定義します。

2021年現在では1s（s:second、秒）は以下のように定義されています。

すみません、物理のことはよくわからないのですが。

調べてみると、セシウム原子に高周波を当てて、構造が変わるまでが1秒とか、セシウムが電磁波を出しており、その間隔の何億分の1が1秒とかありましたが、本当が何かがわかりませんでした。

とにかく、人類が地球を飛び出したとしても、光とセシウムがあれば時間と長さが分かるわけです。

長さを地球の本初子午線を基準に考えていた時期もあったのですが、これだと地球外には適用できないですよね。

宇宙のどこにいても長さと時間は測れるようにしようという試みが読み取れます。

速さ

さて、ここで速さの定義です。

長さと時間は光の速さとセシウムを基準に考えていました。

では速さは何を基準に考えていたか、と思ってるかと思いますが

速さには基準など存在しません。

例えば

そうです。

速さだけは仲間外れなのです。

想像してください。

あなたが今持っている物は、どんな長さでも測れる物差しと、どんな時間でも測れる時計です。

この2つの物差しで速さも分かるわけです。

速さがあらかじめ分かっている問題もありますが、それは距離、時間は忘れたけど、速さを測ってみたらこうだったという解釈ができます。

もしくは、自動車って大体速さこれくらいだよねとか自転車って大体速さこれくらいだよねという推測の元で成り立っています。

速さを測るスピードガンも距離と時間から速さを算出しているはずです。

長さ、時間、速さの概念から解く

長さ、時間、速さの概念が分かれば問題は解けるはずです。

道のりを求める場合

速さの定義は「単位時間あたりどのくらい距離進むか」ということでした。

例えば、$5m/s$なら、$1$秒で$5m$なので、$2$秒で$10m$、$3$秒で$15m$進みます。

つまり、$(道のり) = (速さ) × (時間)$

です。

速さを求める場合

速さの定義「単位時間あたりどのくらい距離進むか」からわかります。

例えば、$5m$進むのに$10秒$かかったのであれば、$1秒(1分、1時間)$でどのくらい進んだかが速さなので

$5(m) ÷ 10(s) = 0.5(m/s)$

です。

また、先ほど道のりを求めた時をイメージしてもよいです。

$(道のり) = (速さ) × (時間)$

今回知りたいのは速さなので、割り算さえできれば

$(速さ) = (道のり) ÷ (時間)$

ということはわかるでしょう。

時間を求める場合

速さで割る、というイメージがつきづらいので

$(道のり) = (速さ) × (時間)$

から

$(時間) = (道のり) ÷ (速さ)$

を出すのがよいかと思います。

単位で覚える

そんなの学生には難しい！という方のためにもう一つ方法があります。

単位で覚えましょう。

そもそも、速さの単位$m/s$というのは

$$m/s = \frac{m}{s} = \frac{道のり}{速さ}$$

からなっています。

ここからでも公式は割り出せますよね。

$$(道のり) = m = s × \frac{m}{s} = (時間)×(速さ)$$

$$(時間) = s = m × \frac{s}{m} = m ÷ \frac{m}{s} = \frac{(道のり)}{(速さ)}$$

この単位による公式の作り方は、距離、時間、速さ以外でも使えます。

$$(圧力) = Pa = N/m^2 = N/m^2 = \frac{力}{面積}$$

$$(加速度) = m/s^2 = (m/s)/s = \frac{(速さ)}{(時間)}$$

$$(年収) = 円/年$$

$$(人口密度) = 人/km^2 = \frac{(人)}{(面積)}$$

まとめ

・公式は作るもの
・長さ、時間は光とセシウムがあれば測ることができ、速さは長さと時間が分かれば作れる
・道のり、速さ、時間の概念から考える
・難しければ単位から覚える

余談

等速の場合では$「(道のり)=(速さ)×(時間)」$と、比例でよいのですが、加速度を含めると積分を使って道のりを算出したりします。

積分を使う方法は割愛させていただきます。