三角グラフとヴィヴィアーニの定理
本稿では,3要素の構成比を表現できる三角グラフについて簡単に触れたのち,それが持つ幾何学的性質を主張するヴィヴィアーニの定理およびその拡張版を証明する.
三角グラフ
三角グラフとは,3つの要素で構成されるデータについて,それらの占める割合を表す際に用いられるグラフである.3要素の構成比は,正三角形内部のある点から各辺におろした垂線の長さで表現される.
下記の三角グラフは,国語の学習時間全体に対して現代文,古文,漢文が占める割合を表したものである.この図からは,学習時間が古文,現代文,漢文の順に長いことが読み取れる.
 三角グラフの例
三角グラフの例
ところで,3要素の占める割合をこのように表すことは適切だろうか.その答えを与えるのがヴィヴィアーニの定理である.
ヴィヴィアーニの定理
ヴィヴィアーニの定理(Viviani's theorem)は,正三角形に関する初等幾何学の定理である.定理の主張は大変興味深いが,面積に注目すれば証明は単純明快である.
正三角形の内部の点から各辺に下ろした垂線の長さの和は,点の位置によらず一定である.
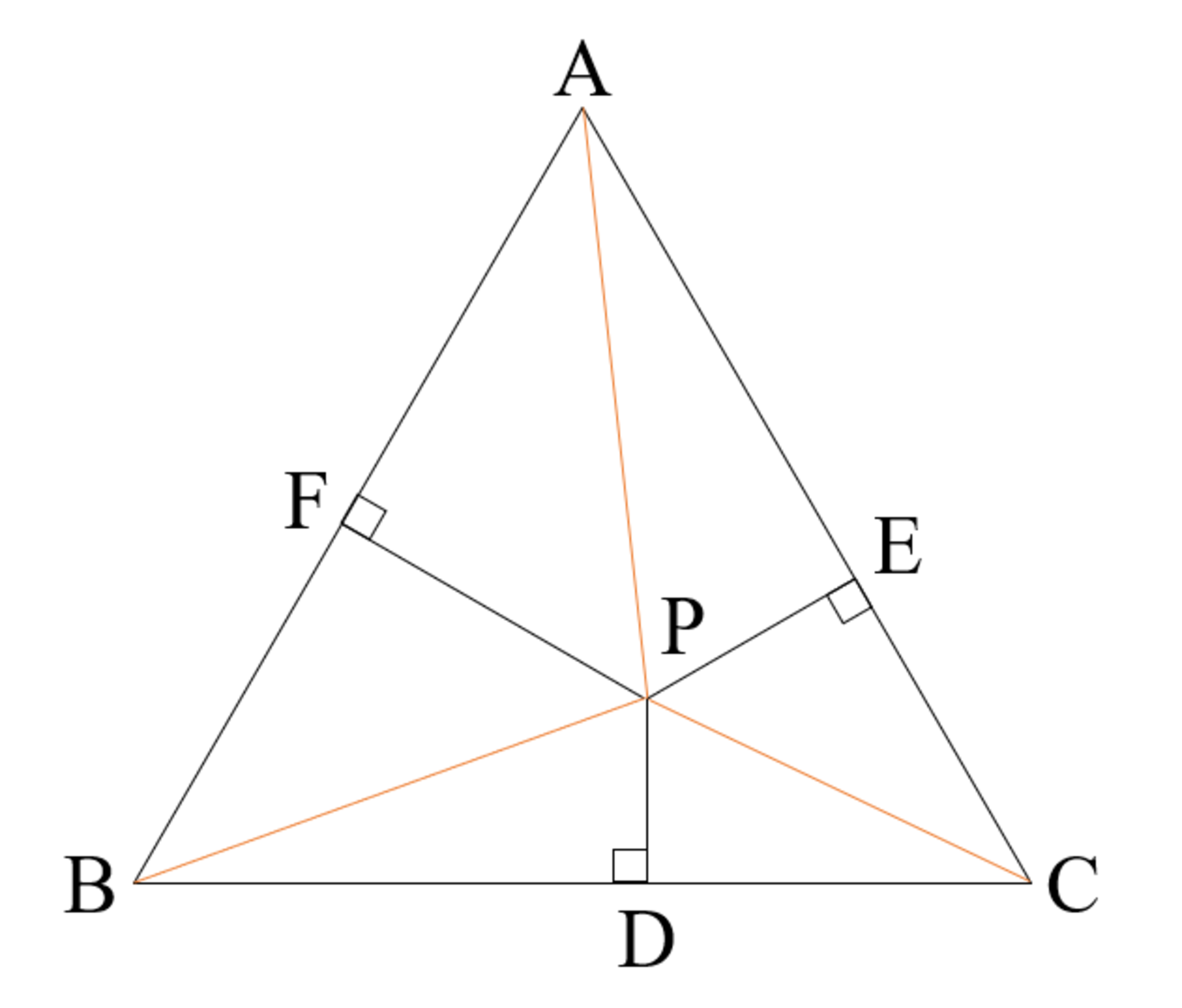
正三角形$\mathrm{ABC}$の内部の点を$\mathrm{P}$とし,点$\mathrm{P}$から辺$\mathrm{BC}, \mathrm{CA}, \mathrm{AB}$に下ろした垂線と各辺との交点をそれぞれ$\mathrm{D}, \mathrm{E}, \mathrm{F}$とする.
 正三角形と3垂線
正三角形と3垂線
定理を証明するには,$\mathrm{PD}+\mathrm{PE}+\mathrm{PF}$が$\mathrm{P}$によらない定数であることを示せばよい.
 正三角形を分割する3つの三角形に注目する
正三角形を分割する3つの三角形に注目する
正三角形$\mathrm{ABC}$および$\triangle\mathrm{PBC}, \triangle\mathrm{PCA}, \triangle\mathrm{PAB}$の面積に注目すると
$$
\begin{align}
\triangle\mathrm{ABC}
&=\triangle\mathrm{PBC}+\triangle\mathrm{PCA}+\triangle\mathrm{PAB} \\
&=\frac{1}{2}\cdot\mathrm{BC}\cdot\mathrm{PD}+\frac{1}{2}\cdot\mathrm{CA}\cdot\mathrm{PE}+\frac{1}{2}\cdot\mathrm{AB}\cdot\mathrm{PF} \\
&=\frac{1}{2}\cdot\mathrm{AB}\cdot\mathrm{PD}+\frac{1}{2}\cdot\mathrm{AB}\cdot\mathrm{PE}+\frac{1}{2}\cdot\mathrm{AB}\cdot\mathrm{PF}(\because\mathrm{AB}=\mathrm{BC}=\mathrm{CA})\\
&=\frac{1}{2}\cdot\mathrm{AB}\cdot(\mathrm{PD}+\mathrm{PE}+\mathrm{PF})
\end{align}
$$
より
$$
\mathrm{PD}+\mathrm{PE}+\mathrm{PF}=2\frac{\triangle\mathrm{ABC}}{\mathrm{AB}}
$$
となる.従って,$\mathrm{PD}+\mathrm{PE}+\mathrm{PF}$は$\mathrm{P}$によらないから,定理は示された.
証明より,$\mathrm{PD}+\mathrm{PE}+\mathrm{PF}$の値は正三角形の高さに等しくなることがわかる.
ヴィヴィアーニの定理より,三角グラフに描かれた3つの線分の長さの和は,内部の点の位置によらず常に一定である.この事実は,3要素の構成比を三角グラフによって表すことが妥当であることを保証している.
ヴィヴィアーニの定理の拡張
鋭い読者ならば,ヴィヴィアーニの定理の証明を読んで「これって三角形じゃなくても成り立つのでは?」と思うかもしれない.実際その通りであり,ヴィヴィアーニの定理は正$n$角形に拡張できる.この証明は,よくある数学書なら演習問題にされるだろうし,筆者的にもその方が読者のためになると思うが,念のため証明を載せておく.証明の方針は,正三角形の場合と全く同じである.
正$n$角形($n\geq3$)の内部の点から各辺に下ろした垂線の長さの和は,点の位置によらず一定である.
正$n$角形$\mathrm{A}_1\mathrm{A}_2\cdots\mathrm{A}_n$の内部の点を$\mathrm{P}$とし,点$\mathrm{P}$から辺$\mathrm{A}_1\mathrm{A}_2, \mathrm{A}_2\mathrm{A}_3, \cdots, \mathrm{A}_{n-1}\mathrm{A}_n, \mathrm{A}_n\mathrm{A}_1$に下ろした垂線と各辺との交点をそれぞれ$\mathrm{B}_1, \mathrm{B}_2, \cdots, \mathrm{B}_{n-1}, \mathrm{B}_n$とする.定理を証明するには,$\mathrm{PB}_1+\mathrm{PB}_2+\cdots+\mathrm{PB}_n$が$\mathrm{P}$によらない定数であることを示せばよい.
正$n$角形$\mathrm{A}_1\mathrm{A}_2\cdots\mathrm{A}_n$の面積を$S$とすると,
$$
\begin{align}
S
&=\sum_{k=1}^n\triangle\mathrm{PA}_k\mathrm{A}_{k+1}(\mathrm{A}_{n+1}=\mathrm{A}_1とする) \\
&=\sum_{k=1}^n\frac{1}{2}\cdot\mathrm{A}_k\mathrm{A}_{k+1}\cdot\mathrm{PB}_k \\
&=\sum_{k=1}^n\frac{1}{2}\cdot\mathrm{A}_1\mathrm{A}_2\cdot\mathrm{PB}_k(\because\mathrm{A}_1\mathrm{A}_2=\mathrm{A}_2\mathrm{A}_3=\cdots=\mathrm{A}_n\mathrm{A}_1)\\
&=\frac{1}{2}\cdot\mathrm{A}_1\mathrm{A}_2\cdot\sum_{k=1}^n\mathrm{PB}_k
\end{align}
$$
より
$$
\mathrm{PB}_1+\mathrm{PB}_2+\cdots+\mathrm{PB}_n=2\frac{S}{\mathrm{A}_1\mathrm{A}_2}
$$
となる.従って,$\mathrm{PB}_1+\mathrm{PB}_2+\cdots+\mathrm{PB}_n$は$\mathrm{P}$によらないから,定理は示された.
$n=4$のとき,上記の定理は自明である(図を描いてみよ).
