Carnotの定理を証明してみた
始めに
こんにちは、ちぇんです。
今日は初等幾何のちょっとマイナーな定理、Carnotの定理を自分のtex打ちの練習も兼ねて私なりに証明してみたいと思います。まずはその主張を見てみます。
鋭角三角形$ABC$において外接円の半径を$R$.内接円の半径を$r$とすれば下図において以下が成り立つ
$OE+OF+OG=R+r$
(ただし$E.F.G$は各辺の中点)
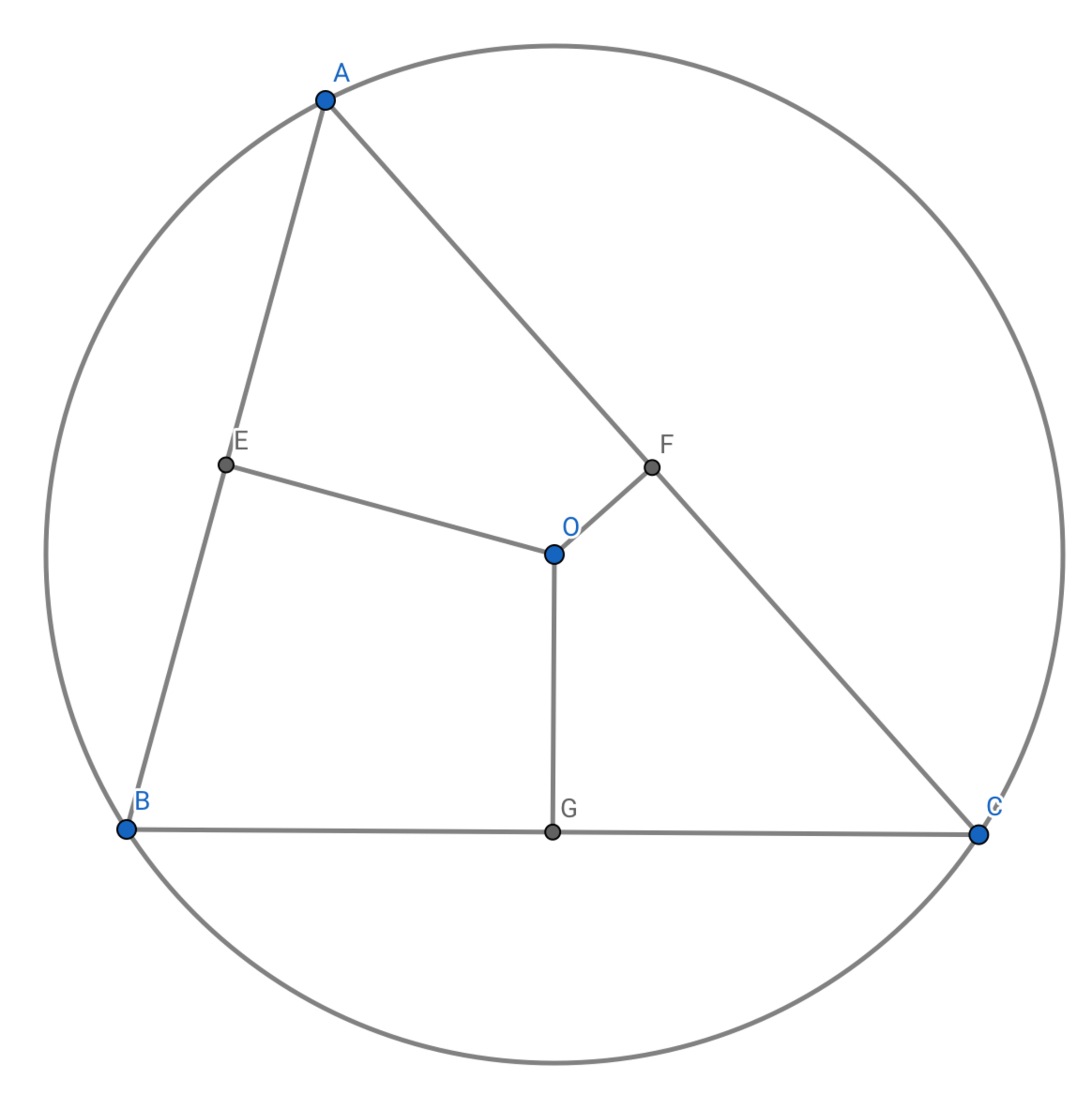 下図
下図
うーん、なかなか美しい。外心から下ろした垂線$3$つの和が外接円、内接円双方の和に等しいのはなかなか想像がつかず、面白いですよね。そんなこの定理を証明してみましょう。そこまで難しいものではないです。必要な前提知識はトレミーの定理のみなので、初等幾何があまり得意でない方も十分読めると思います。
定理の証明
ここでは式変形の便宜上$AF=b,OF=O_b,CG=a,OG=O_a,AE=c,OE=O_c$
とします。
このとき$4$点$AOEF,BOEG,COFG$はそれぞれ共円です。(対角の和がそれぞれ$180^\circ$になっているためです。図2を参照)よってここに先程話したトレミーの定理を適用すれば、
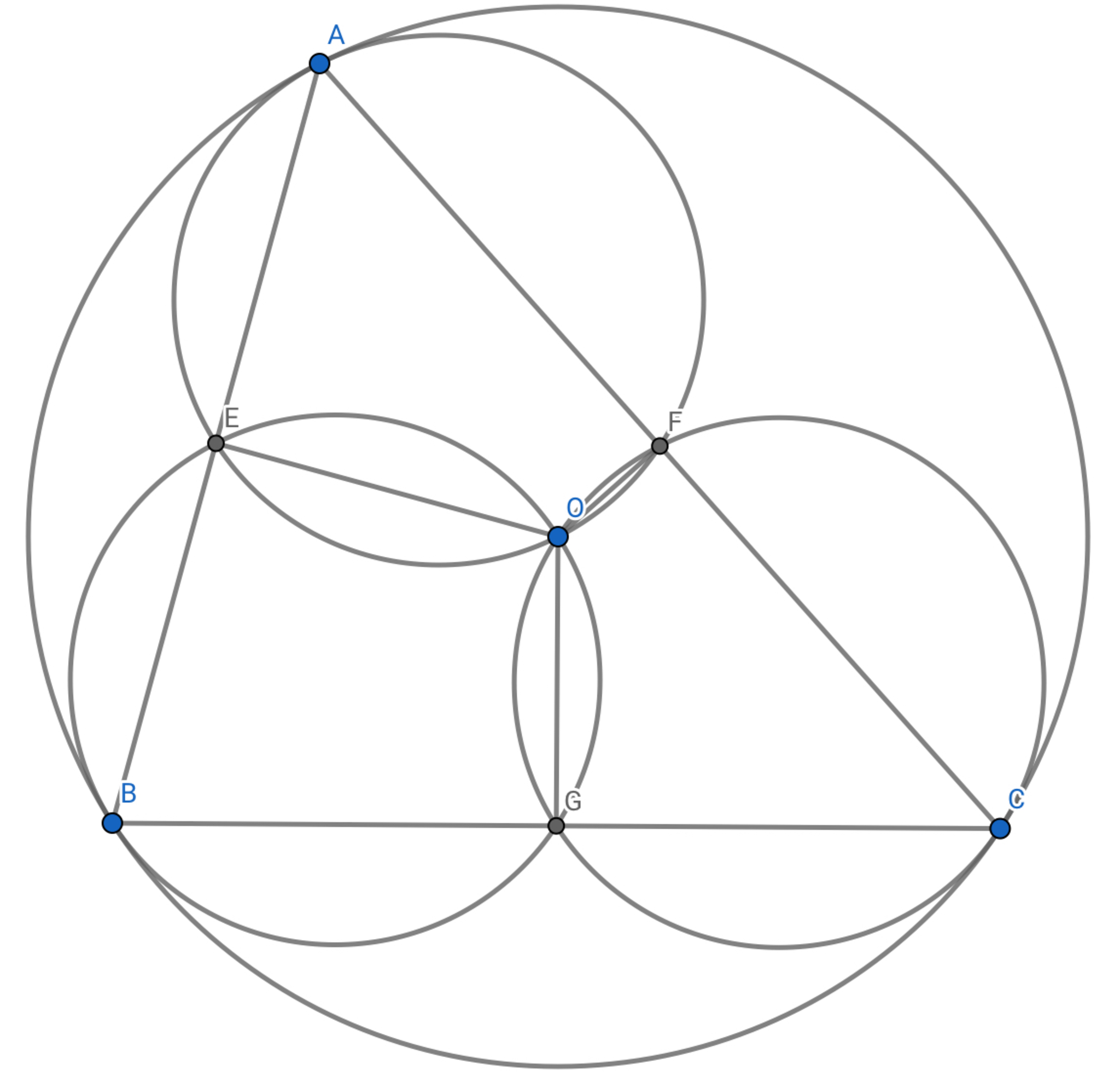 図2
図2
$O_ab+O_ba=Rc,O_cb+O_bc=Ra,O_ca+O_ac=Rb$
の$3$式が導けます。これらを全て足し合わせることで
$O_a(b+c)+O_b(a+c)+O_c(a+b)=R(a+b+c)$
が従います。
またこの三角形の面積を$S$とすれば、内接円の半径$r$について、$\dfrac{1}{2}(2a+2b+2c)r=S$となります。$(2a=BC,2b=AC,2c=AB)$
加えて三角形$ABC$を外心で三分割して考えれば、$O_aa+O_bb+O_cc=S$も言えます。以上で証明に必要な式は全て出揃いました。後は式変形するのみです。
そうすると
$O_a(b+c)+O_b(a+c)+O_c(a+b)+O_aa+O_bb+O_cc$
$=(O_a+O_b+O_c)(a+b+c)$
$=R(a+b+c)+r(a+b+c)$
$=(R+r)(a+b+c)$
このようになり、後は$2$行目と$4$行目の式を$a+b+c$で割れば題意を得ます!
終わりに
如何でしたでしょうか。この定理はwikipediaに証明が無いし、ネットで見つけた証明をそのまま書くのもつまらないので私が考えた証明を書きました。実はこの定理、鈍角三角形に対しても拡張ができます。ただしその場合は符号付き距離など細かい議論が必要とされるので今回は鋭角三角形のときのみの証明としました。またこれからもゆる〜く初等幾何の話をしていければと思ってます。ここまでお読みいただきありがとうございました。
