Kiepert双曲線を用いたLesterの定理の証明
今回は比較的最近(1997)にLester Juneによって提示,証明されたLesterの定理を多少寄り道しながらですが,証明しようと思います.ぜひ最後までお読みください.以下,常体.
導入
$Lester$の定理の前に予備知識として次の定理を証明する.
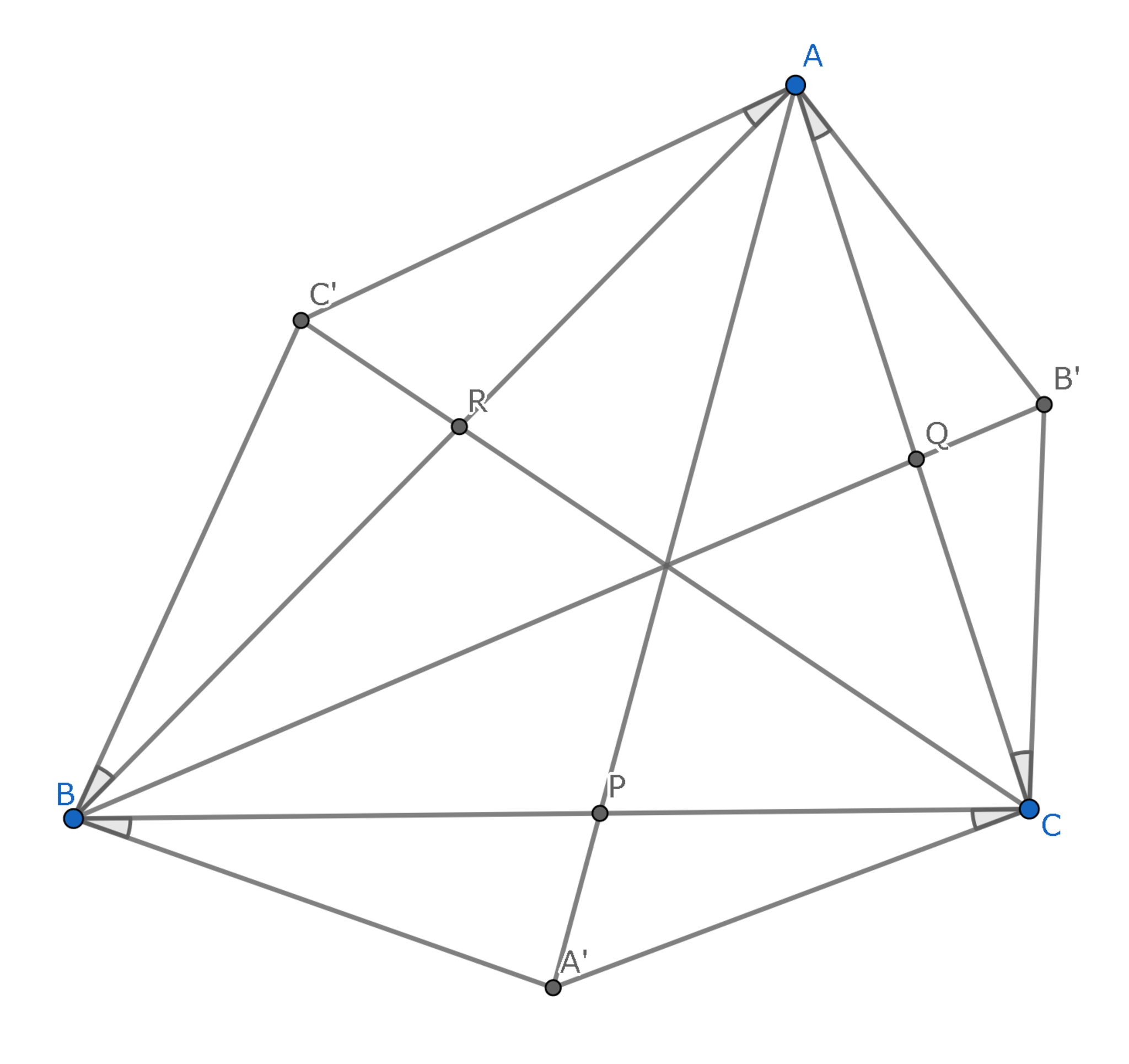
三角形$ABC$があり,点$A^{\prime},B^{\prime},C^{\prime}$が,三角形$A'BC,AB'C,ABC'$が底角が等しい三角形であるとき,3直線$AA',BB',CC'$は一点で交わる.
ただし,それぞれの二等辺三角形の底辺は$BC,CA,AB$とし,底角の向きは三角形$ABC$の外側を正とする.
等しい底角を$\theta$とする.直線$AA'$と直線$BC$の交点を$P$とすると
$BP:CP=|ABA'|:|ACA'|=AB\cdot BA'\cdot \sin\angle ABA':AC\cdot CA'\cdot \sin\angle ACA=AB\sin(B+\theta):AC\sin(C+\theta)$
同様に$BB'$と$CA$の交点,$CC'$と$AB$の交点をそれぞれ$Q,R$とすると
$CQ:AQ=BC\sin(C+\theta):BA\sin(A+\theta),AR:BR=CA\sin(A+\theta):CB\sin(B+\theta)$が成り立つので
$BP\cdot CQ\cdot AR=CP\cdot AQ\cdot BR$である.
よってチェバの定理の逆より示された.
 命題1 図
命題1 図
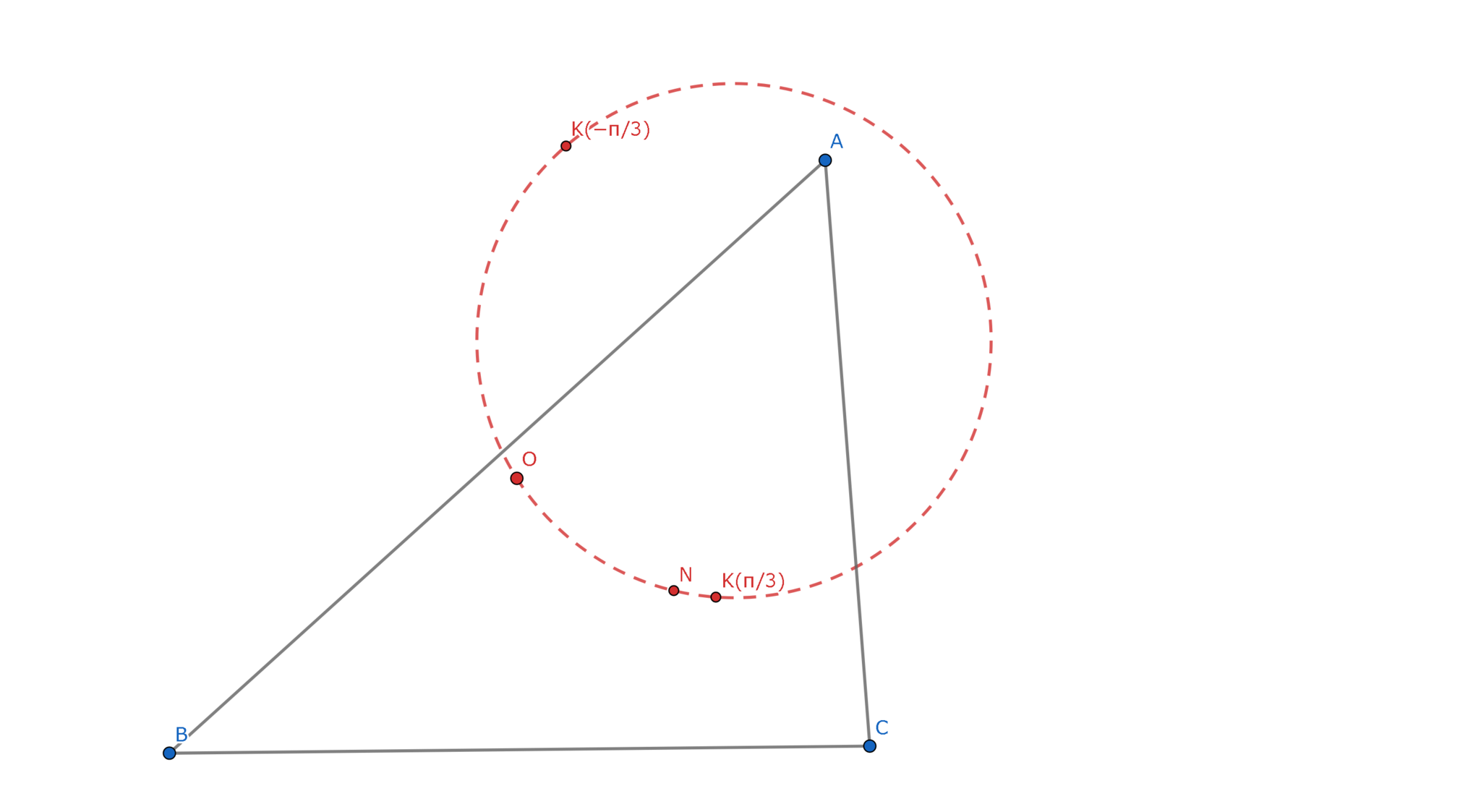
定理1において底角を$\theta$$(-\frac{\pi}{2}\lt\theta\lt\frac{\pi}{2})$としたとき3直線の交点を$K(\theta)$と定義する.
$K(0^{\circ})=G$(重心),$K(-A)=A,\lim_{\theta\to\frac{\pi}{2}}K(\theta)=H$(垂心)
念のため次の語句も導入する.
三角形$ABC$において3辺の中点を通る円を三角形$ABC$の九点円と定義する.
ようやく$Lester$の定理のお出ましである.
任意の不等辺三角形$ABC$について外心,九点円の中心,$\displaystyle K(\frac{\pi}{3}),K(-\frac{\pi}{3})$は同一円周上にある.
 Lesterの定理
Lesterの定理
以下,必要な諸命題を示していく.
A
三角形$ABC$の外心,重心,九点円の中心,垂心をそれぞれ$O,G,N,H$とするとこの4点はこの順に同一直線上にあり,$OG:GN:NH=2:1:3$である.
三角形$ABC$の外接円の半径を$R$,辺$BC$の中点を$M$とする.
$OM=R\cos A$
$AH=AC\cdot\sin(90^{\circ}-A)\cdot\sin^{-1}(180^{\circ}-B)=2R\cos A$
より$OM:AH=1:2$であり,また,$OM/\!/AH$なので$OH,AM$の交点は線分$AM$を$2:1$に内分するが,これは重心$G$に一致する.
よって$G$は線分$OH$上にあり,$OG:GH=2:1$が成り立つ.
また,$N$の定義より,三角形$ABC$の3つの中点を結ぶ三角形を三角形$ABC$に移す移動によって$N$は$O$に移る.
すなわち$G$を中心とする$-1/2$倍の相似移動によって$N$は$O$に移るので,$G$は線分$ON$上にあり,$OG:GN=2:1$が成り立つ.
以上より示された.
B
まずは$\displaystyle K(\frac{\pi}{3}),K(-\frac{\pi}{3})$についてより扱いやすい定義を述べる.
異なる2点$I,J$を,三角形$BCI,BCJ$が正三角形になるようにとる.ただし,直線$BC$に関して$A,I$は同じ側にある.
三角形$BCJ$の外接円,三角形$BCI$の外接円と直線$AJ,AI$が再びそれぞれ交わる点は$K(\frac{\pi}{3}),K(-\frac{\pi}{3})$である.
ほぼ同様に議論できるため$K(\frac{\pi}{3})$についてのみ証明する。
三角形$ABC$の外側に三角形$ACK$が正三角形になるように点$S$をとる.$K(\frac{\pi}{3})$は線分$AJ,BS$の交点である.
このとき三角形$BCS$は三角形$ACJ$を$\frac{\pi}{3}$だけ回転させたものだから$\angle BK(\frac{\pi}{3})J=\frac{\pi}{3}$である.
よって円周角の定理の逆より$K(\frac{\pi}{3})$三角形$BCJ$の外接円上にあるのでこれで示された.
補題4で改めた定義を用いて次の命題を示す.
三角形$ABC$について重心と垂心の中点を$X$としたとき,$\displaystyle K(\frac{\pi}{3}),K(-\frac{\pi}{3}),X$は同一直線上にある.
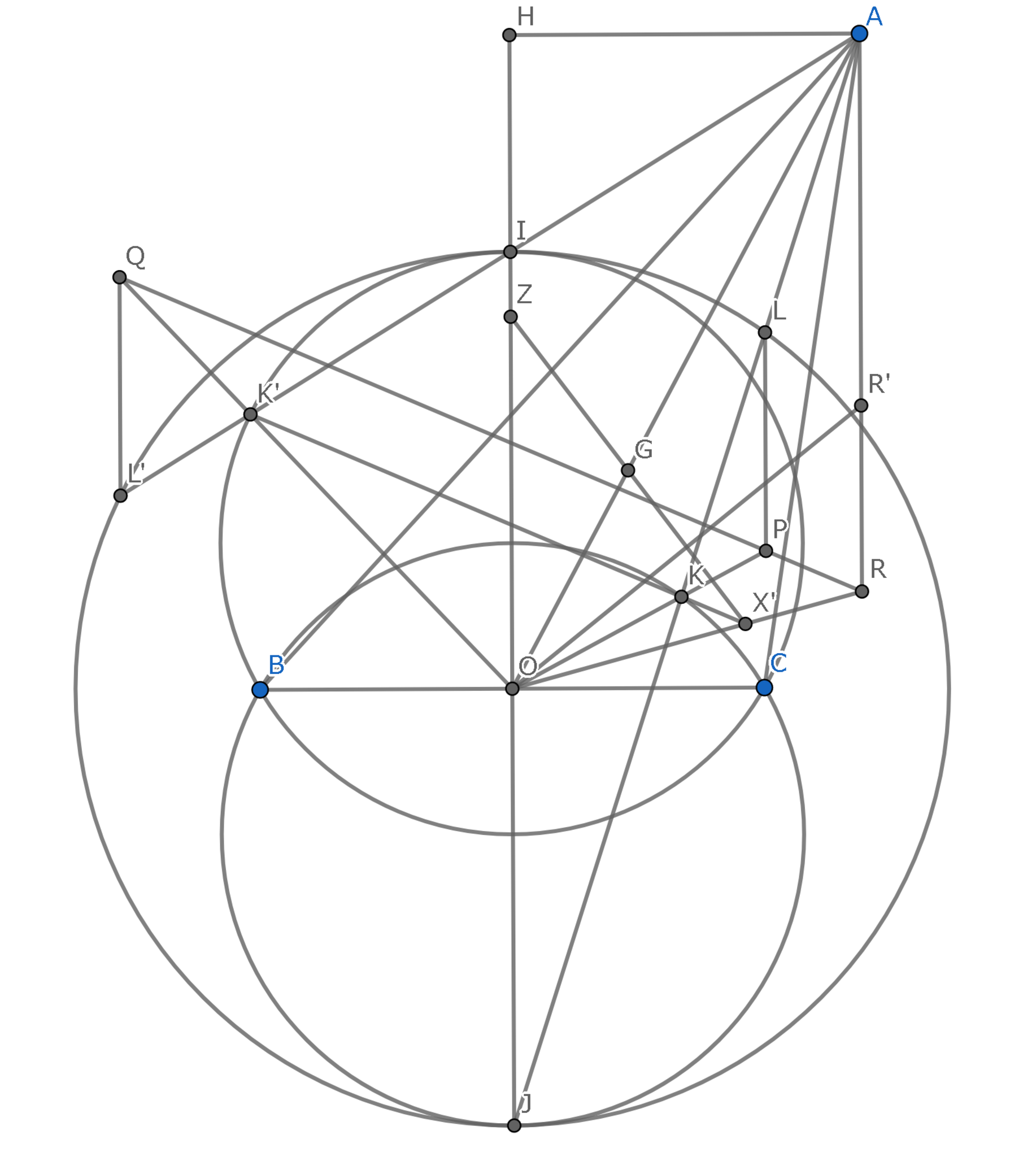
補題4における点$I,J$の定義を用いる.また,便宜上$K(\frac{\pi}{3})$を$K$,$K(-\frac{\pi}{3})$を$K'$と表記する.辺$BC$の中点を$O$とする.
命題3より$X$は,重心$G$に関して外心と対称な点である.線分$AG$の中点を通り線分$BC$に垂直な直線と直線$KK'$の交点を$X'$とし,$G$に関して$X'$と対称な点$Z$が三角形$ABC$の外心であることを示せばよい.
線分$IJ$を直径とする円を$\omega$として半径を$r$とする.
示すべきは$OZ^2+\frac{r^2}{3}=ZA^2$である.
直線$AJ,AI$と$\omega$が再び交わる点をそれぞれ$L,L'$とする.前出の2円と$\omega$の半径比を考えると$JK:KL=IK':K'L'=2:1$である.
したがって$O$を中心とする倍率$3/2$の拡大移動によって$K,K',X'$が移る点をそれぞれ$P,Q,R$とすると$PL=QL'=r/2$であり,$PL,QL,AR/\!/IJ$である.
線分$AR$を$2:1$に内分する点を$R'$とすれば$OZ=AR',ZA=OR'$なので
示すべきは$AR'^2+\frac{r^2}{3}=OR'^2$である.
点$A$から直線$IJ$へ下ろした垂線の足を$H$とすると$OR'^2=(OH-AR')^2+AH^2=OA'^2-2OH\cdot AR'+AR'^2$なので示すべき式は
$OA^2-2OH\cdot AR'=\frac{r^2}{3}$となる.
さらに中線定理を用いて変形すれば結局
$AI^2+AJ^2-4OH\cdot AR'=\frac{8}{3}r^2$ を示せばよい.
 命題5 図1
命題5 図1
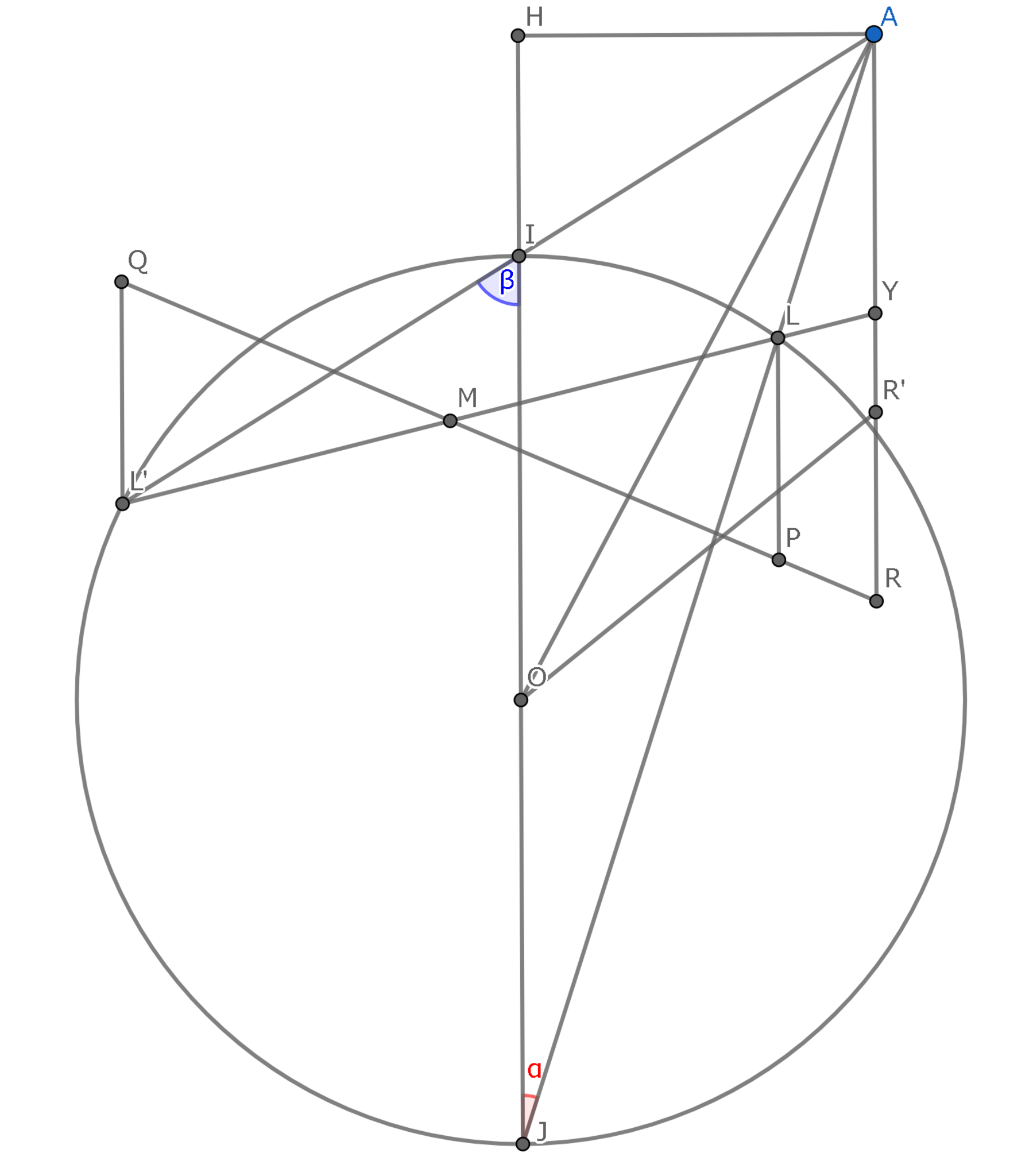
線分$LL'$の中点を$M$とすると,$M$は直線$PQ$上にある.
また,直線$LL',AR$の交点を$Y$とする.
以下,$\angle LJI=\alpha,\angle L'IJ=\beta$とする.$\beta>\alpha$として一般性を失わない.
$AI,AJ,OH,AR'$を$\alpha,\beta,r$のみで表す.
$\displaystyle AI=IJ\cdot\frac{\sin(\pi-\alpha)}{\sin(\beta-\alpha)}=2r\cdot\frac{\sin\alpha}{\sin(\beta-\alpha)}$ 同様に$\displaystyle AJ=2r\cdot\frac{\sin\beta}{\sin(\beta-\alpha)}$
$\displaystyle 2OH=IH+JH=AI\cos\beta+AJ\cos\alpha=2r\cdot\frac{\sin(\alpha+\beta)}{\sin(\beta-\alpha)}$
$\displaystyle AY=AL\cdot\frac{\sin\beta}{\sin(\alpha+\beta)}=AI\cdot\cos(\beta-\alpha)\cdot\frac{\sin\beta}{\sin(\alpha+\beta)}=2r\cdot\frac{\sin\alpha\cdot\sin\beta\cdot\cos(\beta-\alpha)}{\sin(\alpha+\beta)\cdot\sin(\beta-\alpha)}$
$\displaystyle YR=\frac{r}{2}\cdot\frac{MY}{ML}=\frac{r}{2}\cdot\frac{LY+L'Y}{LL'}=\frac{r}{2}\cdot\frac{AL\cdot\frac{\sin\alpha}{\sin(\alpha+\beta)}+AL'\cdot\frac{\sin\beta}{\sin(\alpha+\beta)}}{2r\cdot\sin(\frac{\pi}{2}-\beta+\alpha)}=\frac{r}{2}\cdot\frac{\sin^2\alpha+\sin^2\beta}{\sin(\alpha+\beta)\cdot\sin(\beta-\alpha)}$
したがって$\displaystyle AR'=\frac{2}{3}(AY+TR)=\frac{r}{3}\cdot\frac{\sin^2\alpha+\sin^2\beta+4\sin\alpha\cdot\sin\beta\cdot\cos(\beta-\alpha)}{\sin(\alpha+\beta)\cdot\sin(\beta-\alpha)}$
以上より$AI^2+AJ^2-4OH\cdot AR'=\frac{8}{3}r^2$
$\displaystyle\Longleftrightarrow 4\cdot\frac{\sin^2\alpha+\sin^2\beta}{\sin^2(\beta-\alpha)}-\frac{4}{3}\cdot\frac{\sin^2\alpha+\sin^2\beta+4\sin\alpha\cdot\sin\beta\cdot\cos(\beta-\alpha)}{\sin^2(\beta-\alpha)}=\frac{8}{3}$
$\displaystyle\Longleftrightarrow 3(\sin^2\alpha+\sin^2\beta)-(\sin^2\alpha+\sin^2\beta+4\sin\alpha\cdot\sin\beta\cdot\cos(\beta-\alpha))=2\sin^2(\beta-\alpha)$
これが成り立つことは加法定理および$\sin^2\theta+\cos^2\theta=1$を用いて容易に示される.
以上より所望の式が得られる.
 命題5 図2
命題5 図2
結局計算に頼りましたが割ときれいに収まったので良しとします.
C
この記事では次の有名な事実を用いる.証明は重心座標を用いるが,計算が煩雑で,行列の知識も用いるためこの記事よりも長くなってしまう.なのでこの命題に関してのみ証明を省略させてもらう.
三角形$ABC$について$K(\theta)$の軌跡は直角双曲線である.
この双曲線は$Kiepert$双曲線と呼ばれる.この定理により次がわかる.
頂点$A,B,C$,重心,垂心,$\displaystyle K(\frac{\pi}{3}),K(-\frac{\pi}{3})$は一つの直角双曲線上に乗る.
D
中心が$O$の直角双曲線$\Upsilon$上に4点$A,B,X,Y$があり,$A,B$は異なる枝上にあり,かつ$X,Y$は直線$AB$に関して反対側にあるとする.$\angle AXB=\angle AYB$であるとき,線分$XY$の中点は$O$に一致する.
この証明において角度はすべて有向角とするので示すべきは$\angle AXB+\angle AYB=0^{\circ}$である.
$\Upsilon:Re(z)Im(z)=1,A(a+a^{-1}i),B(b+b^{-1}i),X(x+x^{-1}i),Y(y+y^{-1}i)(b< y<0< x< a)$として一般性を失わない.
$\displaystyle\angle AXB=\arg\frac{(x+x^{-1}i)-(b+b^{-1}i)}{(x+x^{-1}i)-(a+a^{-1}i)}=\arg\frac{a(x-b)(bx-i)}{b(x-a)(ax-i)}=\arg\frac{bx-i}{ax-i}$
同様に$\displaystyle\angle AXB=\arg\frac{by-i}{ay-i}$なので,
$\angle AXB+\angle AYB=0^{\circ}\Longleftrightarrow\displaystyle\frac{(bx−i)(by−i)}{(ax−i)(ay−i)}\in\mathbb{R}$
ここで$\displaystyle\frac{(bx−i)(by−i)}{(ax−i)(ay−i)}=\frac{((a^2xy-1)+a(x+y)i)((b^2xy-1)-b(x+y)i)}{(a^2x^2+1)(a^2y^2+1)}$
分子の虚部を計算すると$(x+y)(b-a)(abxy+1)$であるので,
$\angle AXB+\angle AYB=0^{\circ}\Longleftrightarrow x+y=0$または$abxy=-1$
$b< y<0< x< a$より$x+y=0$がわかるので$X,Y$は点$0$に関して対称.よって示された.
 命題7 図
命題7 図
$A,K(-\frac{\pi}{3})$が直線$BC$に関して反対側にあるとしても対称性を失わず,このとき$\angle BK(\frac{\pi}{3})C=\angle BK(-\frac{\pi}{3})C=\frac{2\pi}{3}$なので系6.1および命題7より次の事実が従う.
線分$\displaystyle K(\frac{\pi}{3})K(-\frac{\pi}{3})$の中点は$Kiepert$双曲線の中心に一致する.
E
中心が$O$の直角双曲線$\Upsilon$の同じ枝上に2点$AB$をとり,線分$AB$の中点を$M$とする.直線$OM$と$\Upsilon$の交点を$P,Q$とすると,$MA^2=MP\cdot MQ$が成り立つ.
$\Upsilon:xy=4$とする.対称性より,$P$の$x$座標は正であるとしてよい.
$A(2a,2a^{-1}),B(2b,2b^{-1})(a,b>0)$とおくと,$M(a+b,a^{-1}+b^{-1})$であるので,
$OM:(a+b)y=(a^{-1}+b^{-1})x$である.この式と$\Upsilon:xy=4$を連立して解いて,
$P(2\sqrt{ab},2\sqrt{a^{-1}b^{-1}}),Q(2\sqrt{ab},2\sqrt{a^{-1}b^{-1}})$を得る.$PO=QO$より
右辺$=MO^2-OP^2=(a+b)^2+(a^{-1}+b^{-1})^2-4ab-4a^{-1}b^{-1}=(a-b)^2+(a^{-1}-b^{-1})^2=$左辺
よって示された.
 命題8 図
命題8 図
命題5における$X$の定義および命題5,系7.1,命題8により次がわかる.
三角形$ABC$の重心を$G$とすると$\displaystyle XG^2=XK(\frac{\pi}{3})\cdot XK(-\frac{\pi}{3})$
必要な道具は以上である.
$Lester$円の存在証明
任意の不等辺三角形$ABC$について外心,九点円の中心,$\displaystyle K(\frac{\pi}{3}),K(-\frac{\pi}{3})$は同一円周上にある.
外心,九点円の中心,重心をそれぞれ$O,N,G,H$とする.命題3よりこの4点は一直線上にあり,$OG:GN:NH=2:1:3$である.この直線と直線$\displaystyle K(\frac{\pi}{3})K(-\frac{\pi}{3})$の交点を$X$とすると命題5より$X$は線分$GH$の中点なので$OG:GN:NX=2:1:1$である.
したがって$XN\cdot XO=XG^2$が成り立つ.
また,系8.1より$\displaystyle XG^2=XK(\frac{\pi}{3})\cdot XK(-\frac{\pi}{3})$なので先ほどの式と合わせて
$\displaystyle XK(\frac{\pi}{3})\cdot XK(-\frac{\pi}{3})=XN\cdot XO$が成り立つ.
以上より方べきの定理の逆から,4点$\displaystyle O,N,K(\frac{\pi}{3}),K(-\frac{\pi}{3})$は同一円周上にある.Q.E.D.
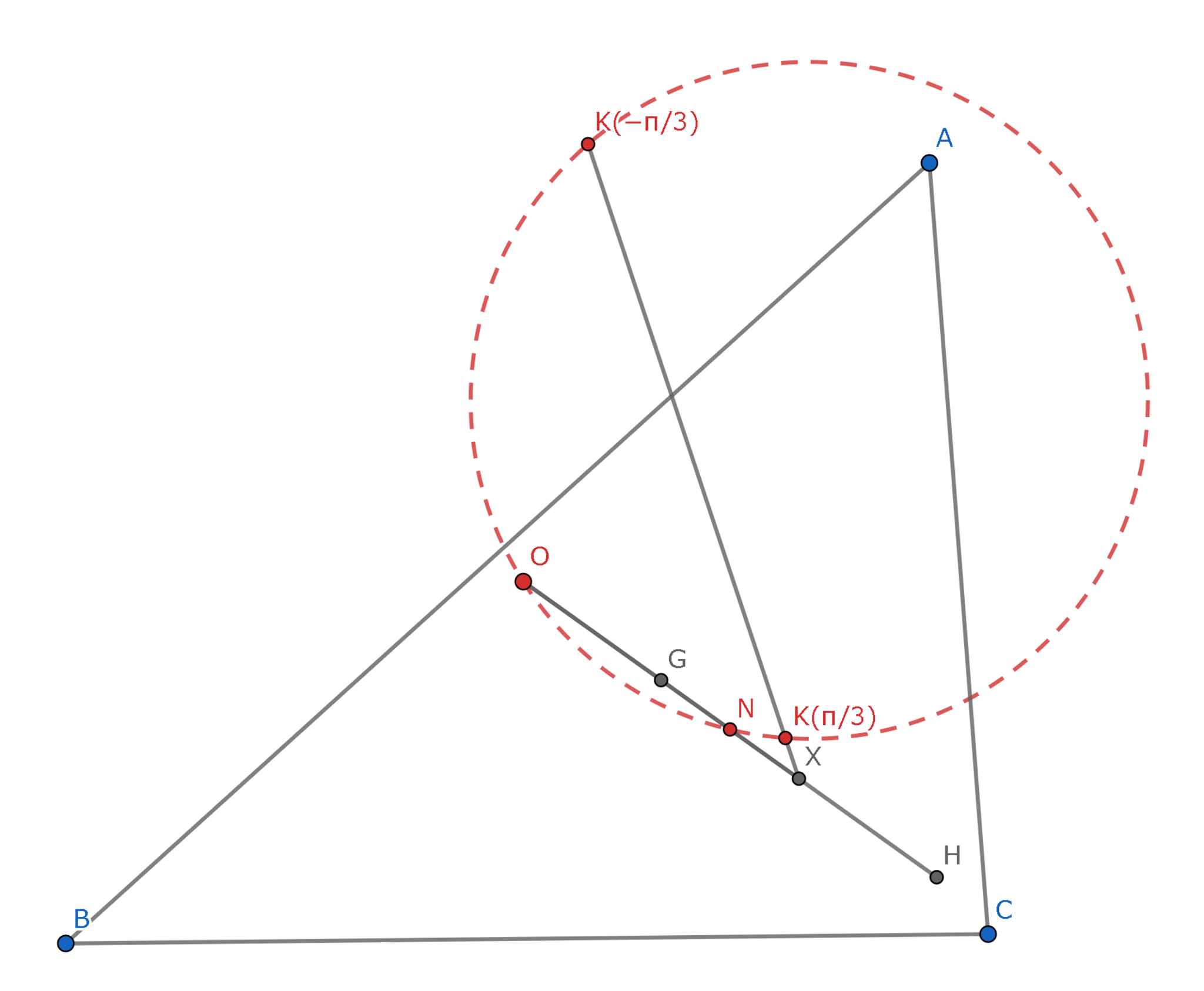 定理9 図
定理9 図
終わりに
いかがだったでしょうか,初等幾何,三角比,直交座標,複素数平面など様々な証明手法でそろえた命題を用いて$Lester$の定理が導けました.いつか定理6にも立ち向かえる数学力をつけたいです.
最後まで読んでいただきありがとうございました.
