【公式を覚えない数学】二次方程式の解
「公式を忘れたから解けない」と思っていませんか？
数学は公式を忘れても、工夫すれば解けるようになっています。
それが、数学がまるで暗記科目かのように言われるので残念でたまりません。
確かに受験など、スピードが求められる場面では公式を覚えた方がよいのですが、忘れたら絶対解けない、ということはありません。
例えば、今回紹介する二次方程式の解は、基礎知識さえあれば簡単に公式を作ることができます。
二次方程式の解の公式を作るために必要な知識
二次方程式の解の公式を作るには、最低限以下の知識が必要です。
$$1.方程式の性質$$
両辺に同じ数を足してもかけても方程式は成り立ちます。
両辺に同じ数を引いても方程式は成り立ちますが、マイナスを足す場合と同じです。
また、両辺に同じ数を割っても方程式は成り立ちますが、分数をかける場合と同じです。
しかも、割り算の場合は0で割ることができないという制限があります。
よって、両辺の同じ数の足し算、かけ算で方程式が成り立つ、とだけ覚えても問題ないです。
$$1-1.両辺に同じ数を足しても方程式は成り立つ$$
極端な話、1=1の両辺に2を足せば3=3になり、方程式は成り立ちます。
移行はこの性質を前提にしているのですが、なかなか覚えてもらえないのが残念です。
$$例：x - 3 = 6$$
$$⇔ x - 3 + 3 = 6 + 3$$
$$⇔ x = 9$$
$$例：2x = x + 6$$
$$⇔ 2x + (-x) = x + 6 + (-x)$$
$$⇔ x = 6$$
$$1-2.両辺に同じ数をかけても方程式は成り立つ$$
極端な話、1=1の両辺に2をかければ2=2になり、方程式は成り立ちます。
$$例：\frac{x}{3}= 6$$
$$⇔ \frac{x}{3} × 3 = 6 × 3$$
$$⇔ x = 18$$
$$例：2x = 6$$
$$⇔ 2x × \frac{1}{2} = 6 × \frac{1}{2}$$
$$⇔ x = 3$$
$$2.式の展開$$
$$(x+α)(x+β)=x^2+(α+β)x+αβ$$
特に$α=β$のとき
$$(x+α)^2=x^2+2αx+α^2$$
では、これで公式を作っていきます。
二次方程式の公式の作り方
$$ax^2 + bx + c = 0 (a≠0)$$
$$⇔x^2 + \frac{b}{a}x + \frac{c}{a} = 0 (∵a≠0、1-2.両辺に\frac{1}{a}をかける)$$
ここで、$(x+α)^2$を利用します。
$α$をどう設定したら$x$が$()$に収まるかを逆算すると
$α=\frac{b}{2a}$とするとうまくいくことがわかります。
$$(x+\frac{b}{2a})^2 = x^2 + \frac{b}{a}x + (\frac{b}{2a})^2 (2.式の展開)$$
$$x^2 + \frac{b}{a}x = (x + \frac{b}{2a})^2 - (\frac{b}{2a})^2 (*)(∵1-1.両辺- (\frac{b}{2a})^2を足す)$$
よって
$$x^2 + \frac{b}{a}x + \frac{c}{a} = 0$$
$$⇔(x+\frac{b}{2a})^2 - (\frac{b}{2a})^2 + \frac{c}{a} = 0$$
$$⇔(x+\frac{b}{2a})^2 = (\frac{b}{2a})^2 - \frac{c}{a} (∵1-1.両辺(\frac{b}{2a})^2 - \frac{c}{a}を足す)$$
$$⇔(x+\frac{b}{2a})^2 = \frac{b^2}{4a^2} - \frac{4ac}{4a^2}$$
$$⇔(x+\frac{b}{2a})^2 = \frac{b^2-4ac}{4a^2}$$
$$⇔x+\frac{b}{2a} = ±\sqrt \frac{b^2-4ac}{4a^2}$$
$$⇔x = ± \frac{\sqrt{b^2-4ac}}{2a} - \frac{b}{2a} (∵1-1.両辺-\frac{b}{2a}を足す)$$
$$⇔x = \frac{-b± \sqrt{b^2-4ac}}{2a}$$
というわけでめでたく二次方程式の解の公式$x = \frac{-b± \sqrt{b^2-4ac}}{2a}$が出てきました。
このように、公式を忘れても知識を応用すれば公式は作ることができます。
スピードは落ちますが、解けないよりはよいでしょう。
平方完成、二次関数
ちょうど平方完成が出てきたので、二次関数の話もしようと思います。
上記の(*)の部分を平方完成と言います。
方程式の解を求めるだけではなく、二次方程式の解析にも使います。
$$x^2 + \frac{b}{a}x = (x + \frac{b}{2a})^2 - (\frac{b}{2a})^2 (*)$$
例えば、二次関数$f(x)= ax^2 + bx + c（a≠0）$があった時に平方完成を使うと以下のようになります。
$$f(x) = a(x^2 + \frac{b}{a}x + \frac{c}{a})$$
$$= a \lbrace (x + \frac{b}{2a})^2 - (\frac{b}{2a})^2 + \frac{c}{a}\rbrace ((*)から)$$
$$= a \lbrace (x + \frac{b}{2a})^2 - \frac{b^2}{4a^2} + \frac{c}{a}\rbrace$$
$$= a(x + \frac{b}{2a})^2 - \frac{b^2}{4a} + c$$
このように、$(x+α)^2$の部分と定数部分に分かれると思いますが、これが重要です。
例えば、$(x-2)^2$のグラフがどうなるかを考えてみます。
| $x$ | $-2$ | $-1$ | $0$ | $1$ | $2$ | $3$ | $4$ |
|---|---|---|---|---|---|---|---|
| $x^2$ | $4$ | $1$ | $0$ | $1$ | $4$ | $9$ | $16$ |
| $(x-2)^2$ | $16$ | $9$ | $4$ | $1$ | $0$ | $1$ | $4$ |
このように、右に2つずつずれていくことが分かります。
次は、$x^2+4$のグラフがどうなるかを考えてみます。
| $x$ | $-2$ | $-1$ | $0$ | $1$ | $2$ | $3$ | $4$ |
|---|---|---|---|---|---|---|---|
| $x^2$ | $4$ | $1$ | $0$ | $1$ | $4$ | $9$ | $16$ |
| $x^2 + 4$ | $8$ | $5$ | $4$ | $5$ | $8$ | $13$ | $20$ |
このように、値が4増えていることが分かります。
よって、これら2つをまとめると以下のようになります。
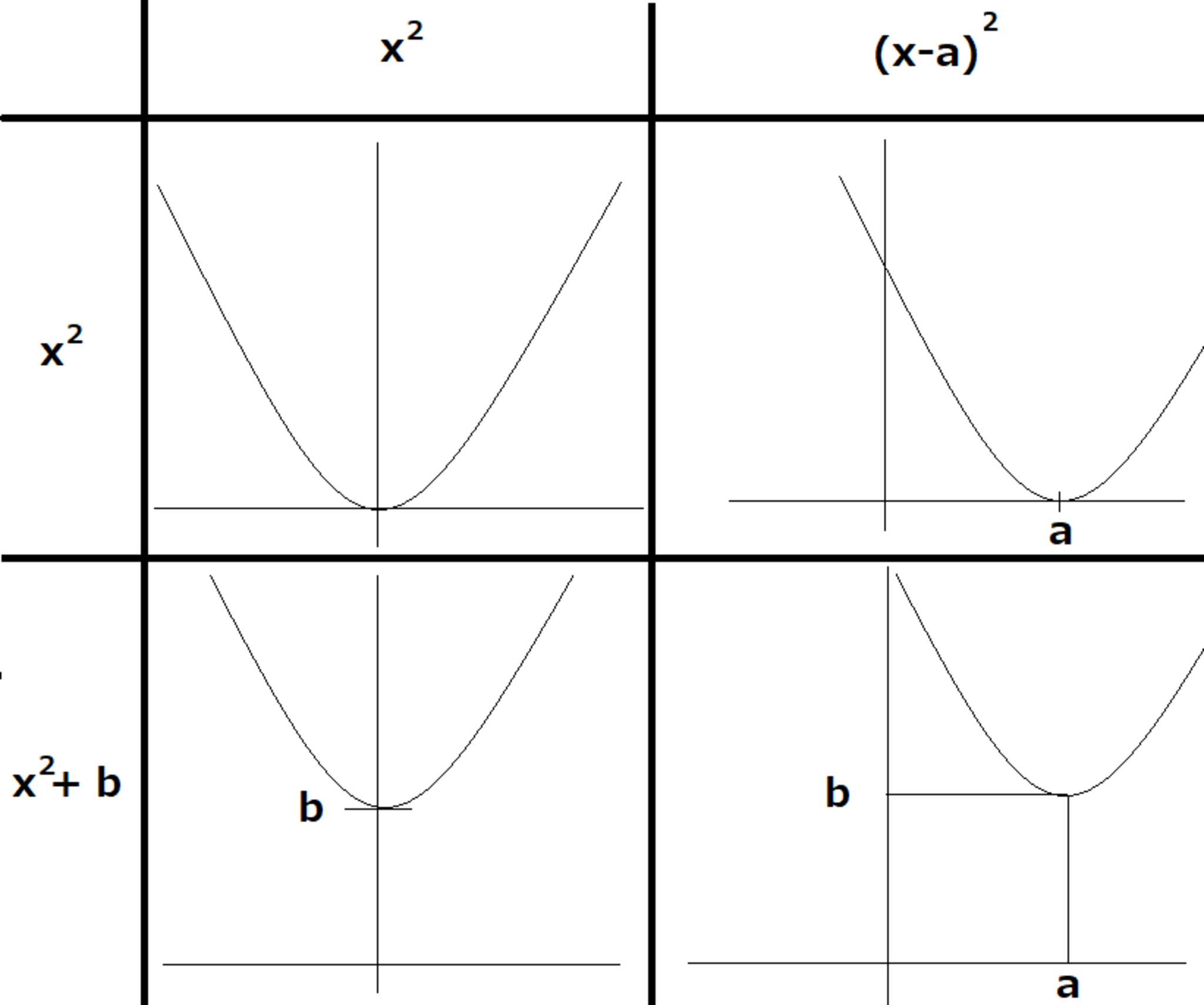二次関数のグラフ
どれも$x^2$を平行移動したものになります。
特に、図の右下の$(a,b)$を頂点と言ったりします。
図の場合、$x^2$の係数が$0$より大きいので下に凸ですが、$0$より小さい場合は上に凸となります。
二次関数の応用(力学)
例えば、物を投げた時の軌道は放物線となります。
この放物線の描く軌道を予測できれば、ある意味予言者になれます。
地球の重力加速度を$9.8(m/s^2)$としたとき、高さ$h(m)$地点から$30°$上に初速$v_0(m/s)$で物を投げた時の$t(s)$経過したときの物体の位置は（空気抵抗は無視する）
$$x(横の位置) = (v_{0}cos30°)t = \frac{\sqrt 3}{2}v_{0}t$$
$$y(縦の位置) = -\frac{1}{2}9.8t^2 + (v_{0}sin30°)t + h$$
$$= -\frac{49}{10}t^2 + \frac{1}{2}v_{0}t + h$$
$t = \frac{2}{\sqrt 3v_0}x$より
$$y = -\frac{49}{10}t^2 + \frac{1}{2}v_{0}t + h$$
$$= -\frac{49}{10}・\frac{4}{3v_{0}^2}x^2 + \frac{1}{2}v_{0}・\frac{2}{\sqrt 3v_0}x + h$$
$$= -\frac{98}{15}x^2 + \frac{\sqrt 3}{3}x + h$$
これは二次関数です。
細かい分析は時間がかかるので割愛します。
これがわかれば、どの軌道で物体が移動するか、どの位置に物体が落下するかまでが分かります。
他にも二次関数の使い道は色々ありますが、一例の紹介でした。
物理計算は以下を参照
【高校物理】道のり、時間、速度、加速度の関係の覚え方
https://youtu.be/3K5Lnzh18Kc
