カタラン数の一般項を簡単に求める

カタラン数の一般項の(おそらく最も簡単な)求め方を発見した。

目次

1. カタラン数とは
2. 普通の格子の経路の代数的な求め方
3. カタラン数の求め方

カタラン数とは

さまざまな定義があるが、今回はこれを定義としておく。

例えば、下図より$c_3=5$である
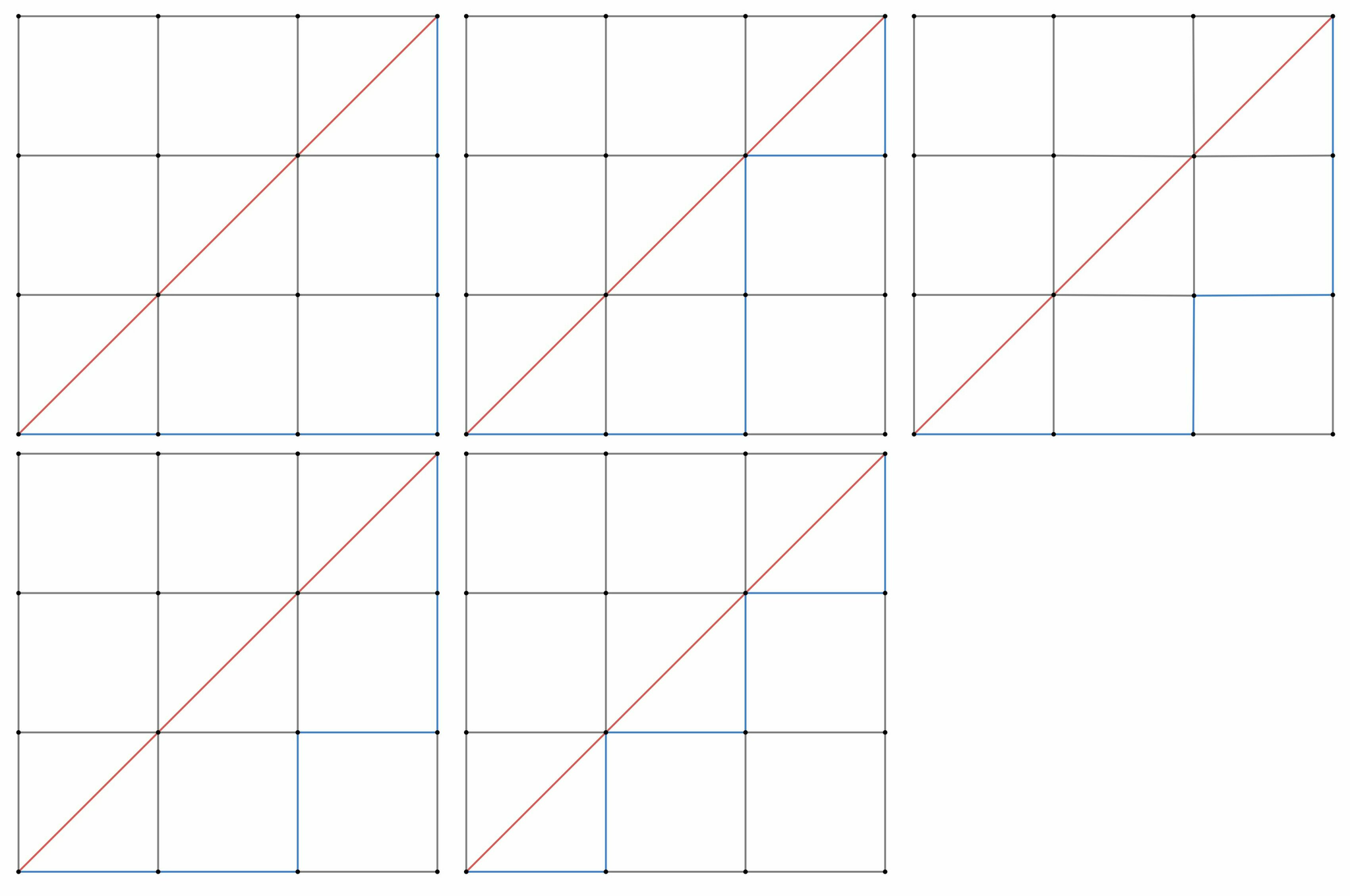カタラン数の例

普通の格子の経路の代数的な求め方

カタラン数でない、普通の経路の場合、以下のように数字を各点に書いて求めることができる。
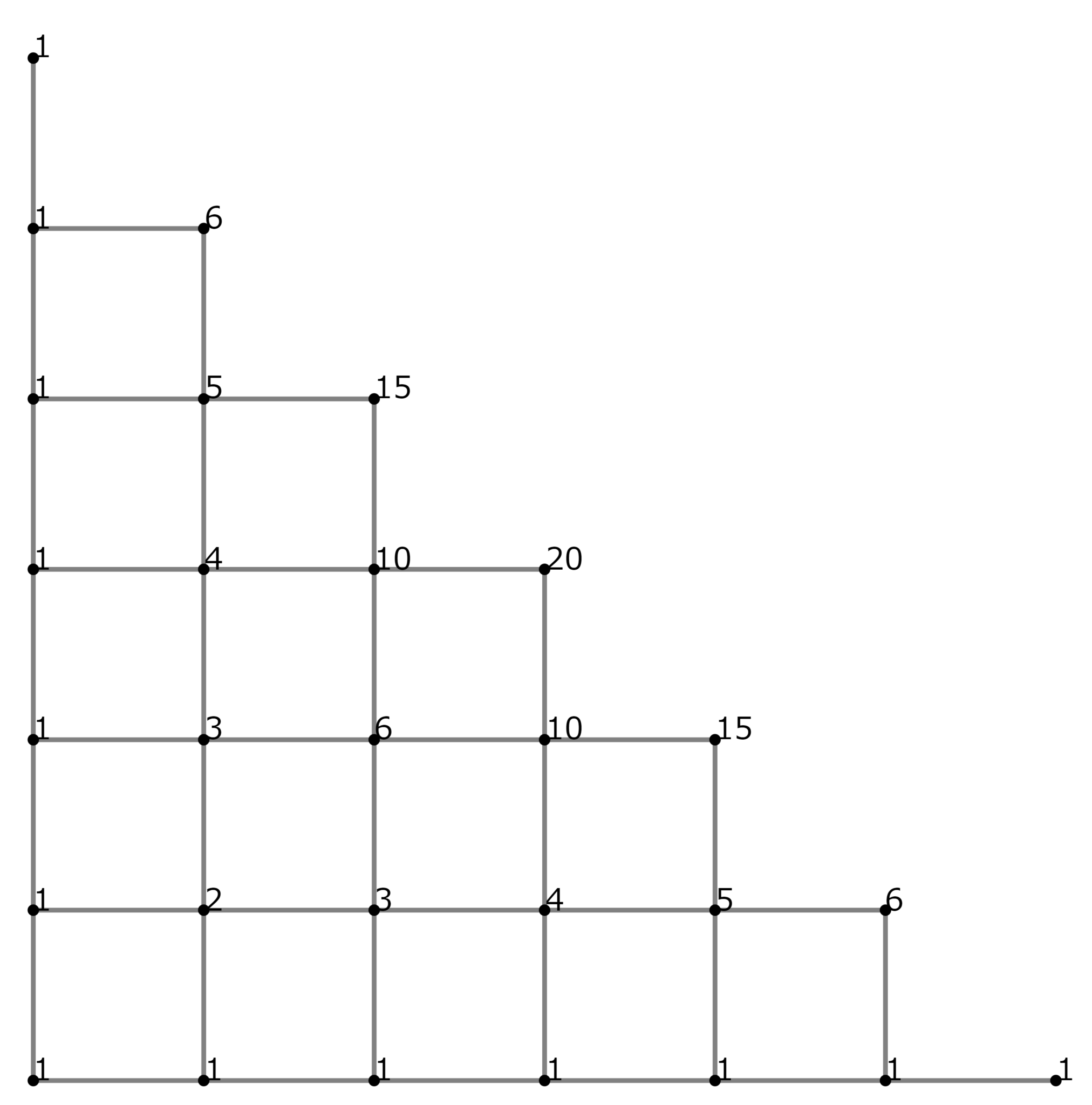普通の格子の経路

ここで、上へ進むときはそのまま($1$をかける)、右へ進むときは$x$をかけるとする。
そうして斜め右肩下がりを一組としてみると、
$1$
$1+x$
$1+2x+x^2$
のように初項$1$、公比$1+x$の等比数列となる。
ここから、格子の最短経路の総数が二項係数になると分かる。

カタラン数の求め方

ここで、下図のように、$1$と$-1$から始める。

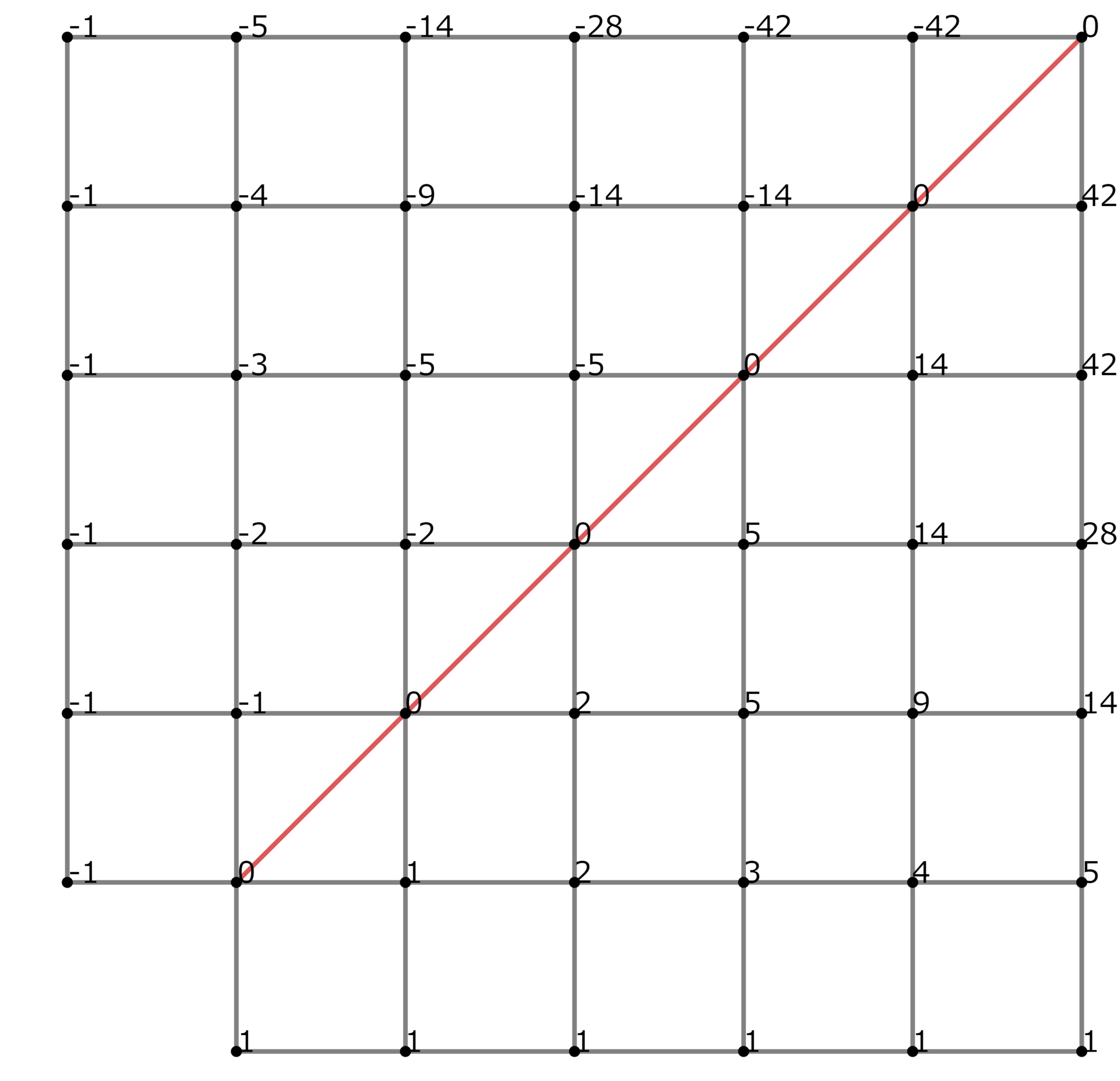カタラン数の求め方

すると、対角線上でちょうど打ち消しあい、線の真下にはカタラン数が並ぶ。
これを同じように斜め右肩下がりを一組としてみると
初項$-1+x$、公比$1+x$の等比数列となる。
つまり第$n$項が$(-1+x)(1+x)^{n-1}$である。

カタラン数$c_n$は第$2n+1$項の$x^{n+1}$の係数、つまり$(-1+x)(1+x)^{2n}$の$x^{n+1}$の係数であるから、
$$ \begin{align*} c_n &= {}_{2n}C_{n}-{}_{2n}C_{n+1}\\ &= \frac{(2n)!}{n!n!}-\frac{(2n)!}{(n+1)!(n-1)!}\\ &= \frac{(2n)!}{n!(n+1)!}(n+1-n)\\ &= \frac{(2n)!}{n!(n+1)!}\\ &= \frac{1}{n+1}{}_{2n}C_{n} \end{align*} $$

したがって、
$$ c_n = \frac{1}{n+1}{}_{2n}C_{n} $$