傾きを共有して切片が異なるデータ列の線形回帰

こんな感じに傾きが同じ複数のデータ列があるときに，傾き$a$と切片たち$b_i$を最小二乗法で解析的に求めたいという問題です．

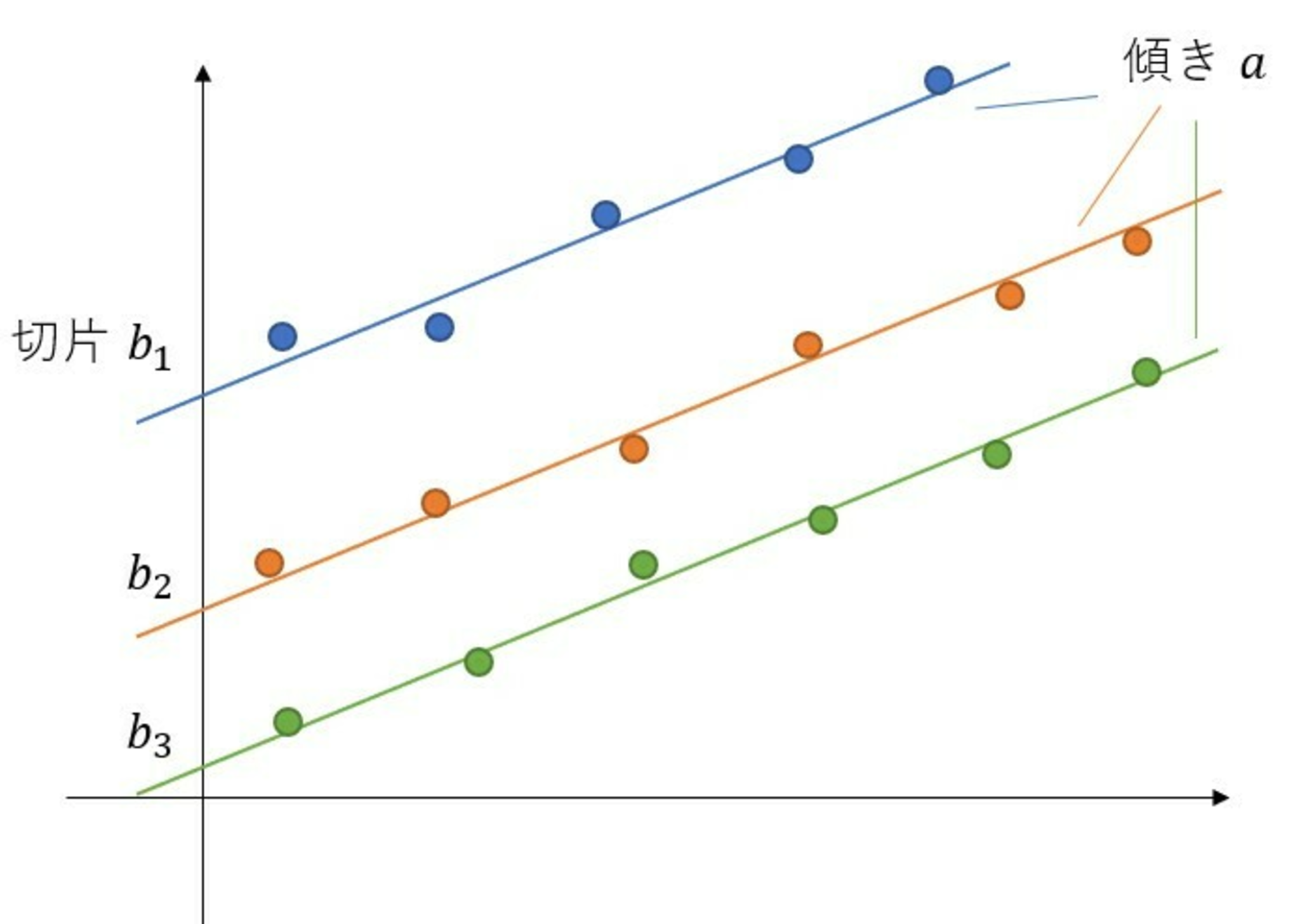データ

研究で必要になって計算したのですがいろいろ計算をミスって手こずったので，せっかくなので残しておこうと思います．
ニッチなシチュエーションですが，アレニウスプロットのように両対数をとって傾きからべきを求めるような解析なんかには使えるかもしれません．

普通の最小二乗法

まず計算の参考にするため，「普通の」最小二乗法の計算を追ってみます．
こちらの計算は[1]の記事を参考にさせていただきました．

最小二乗法による線形回帰は，データが直線
$$ y=ax+b $$
従っているところにノイズが乗っていると考えて，このノイズを最小化する$a, b$を求める問題です．
各データ点を$(x_i,y_i)\;(i=1,\dots,N)$として式で表すと
$$ \underset{a,\ b} {\mathrm{minimize}} \sum_{i=1}^N (y_i-ax_i-b)^2 $$
ここで「ノイズの大きさ」を「差の絶対値」などではなく「差の2乗」で表すのは正規分布の最尤推定との関連と，後述するように微分できた方が計算が簡単であるという都合によるものです．

さて，最小化すべき関数$f(a,b)=\sum_{i=1}^N (y_i-ax_i-b)^2$は係数が1の2次関数を足し合わせたものなので下に凸です．
すなわち最小点は極小点と一致するため$a$と$b$で微分して0になる点が，求めたい$a,\ b$であることが分かります．

よって，$a,\ b$は，連立方程式
$$ \pdiff{f(a,b)}{a} = \sum_i 2x_i(ax_i+b-y_i)=0 \tag{1} $$
$$ \pdiff{f(a,b)}{b} = \sum_i 2(ax_i+b-y_i)=0 \tag{2} $$
を解くと，(2)式を変形して，
$$ a\sum_i x_i + Nb - \sum_i y_i=0 $$
$$ b = \frac1N\sum_i y_i - a\frac1N\sum_i x_i $$

ここで，$\frac1N\sum_{i=1}^N \bullet_i$は$i$についての平均なので$\mean{\bullet}$と表記することにして，
$$ b = \mean{y} - a \mean{x} $$
となります．これを(1)式に代入して整理すると，
$$ \sum_i \p{a x_i^2 + b x_i - x_i y_i}=0 $$
$$ a\frac1N\sum_i\p{x^2}+\p{\mean{y}-a\mean{x}}\cdot\frac1N\sum_i x-\frac1N\sum_i\p{xy}=0 $$
$$ a\mean{x^2}+\p{\mean{y}-a\mean{x}}\cdot\mean{x}-\mean{xy}=0 $$
$$ a\p{\mean{x^2}-\mean{x}^2}-\p{\mean{xy}-\mean{x}\mean{y}}=0 $$
$$ a = \frac{\mean{xy}-\mean{x}\mean{y}}{\mean{x^2}-\mean{x}^2} $$
$$ \therefore\; b = \frac{\mean{x^2}\mean{y}-\mean{x}\mean{xy}}{\mean{x^2}-\mean{x}^2} $$
このようにして，$a,b$の値を求められました．

ちなみに，誤差の大きさは正規分布の最尤推定問題を解くことで$\sigma^2=\mean{\p{ax+b-y}^2}$が得られます．

傾きを共有して切片が異なるデータ

冒頭の図1のように，$k$番目の直線が$y=ax+b_k$，$k=1,\dots,M$のように傾き$a$は共通，切片$b_k$は$k$によって異なるという場合の最小二乗法を考えます．
$k$番目の直線の$i$番目のデータを$(x_{k,i}, y_{k,i})$とすると，この問題は
$$ \underset{a,\ b_1,\dots,b_M} {\mathrm{minimize}} \sum_{k=1}^M \sum_{i=1}^N (y_{k,i}-ax_{k,i}-b_k)^2 $$
と定式化できます．
シグマが増えてややこしくなりましたが，最小化すべき関数$g(a,b_1,\dots,b_M)=\sum_{k} \sum_{i} (y_{k,i}-ax_{k,i}-b_k)^2$は複数の$k$にまたがるような積の項はないため偏微分は簡単で，
$$ \pdiff{g(a,b_1,\dots,b_M)}{a} = \sum_k\sum_i 2x_{k,i}(ax_{k,i}+b_k-y_{k,i})=0 \tag{3} $$
$$ \pdiff{g(a,b_1,\dots,b_M)}{b_k} = \sum_i 2(ax_{k,i}+b_k-y_{k,i})=0\;\;(k=1,\dots,M) \tag{4} $$
の$M+1$連立方程式となります．

(4)式は各$k$について(2)式と同様に解けて，
$$ b_k = \mean{y_k} - a \mean{x_k} $$
です．
これを(3)式に代入し整理すると，
$$ \sum_k \sum_i \p{ax_{k,i}^2+b_kx_{k,i}-x_{k,i}y_{k,i}}=0 $$
$$ \sum_k \p{a\mean{x_k^2}+\p{\mean{y_k} - a \mean{x_k}}\cdot\mean{x_k}-\mean{x_k y_k}}=0 $$
$$ a\sum_k\p{\mean{x_k^2}-\mean{x_k}^2}-\sum_k\p{\mean{x_k y_k}-\mean{x_k}\mean{y_k}}=0 $$
$$ a = \frac{\sum_k\p{\mean{x_k y_k}-\mean{x_k}\mean{y_k}}}{\sum_k\p{\mean{x_k^2}-\mean{x_k}^2}} $$

$k$についての平均$\frac1M\sum_{k=1}^M\bullet_k$を$\B{\bullet}$と表すことにすれば，
$$ a = \frac{\B{\mean{x_k y_k}-\mean{x_k}\mean{y_k}}}{\B{\mean{x_k^2}-\mean{x_k}^2}} $$
となります．

$k$ごとに線形回帰をおこなって$a$をもとめて平均をとる，という方法だと
$$ a' = \B{\frac{{\mean{x_k y_k}-\mean{x_k}\mean{y_k}}}{{\mean{x_k^2}-\mean{x_k}^2}}} $$
となるので少し式が違いますね．

結論：

この場合も，同様に正規分布の最尤推定により$\sigma^2=\B{\mean{\p{ax+b-y}^2}}$が得られます．

Python での計算

文字式ばかりだとピンとこないので，実際に数値計算も行ってみます．
$a=1.5, b_1=0.5, b_2=2.1, b_3=4.3$とし，適当に定めた$x$から$y=ax+b$に$\sigma^2=0.5$のガウスノイズを加えてデータとします．

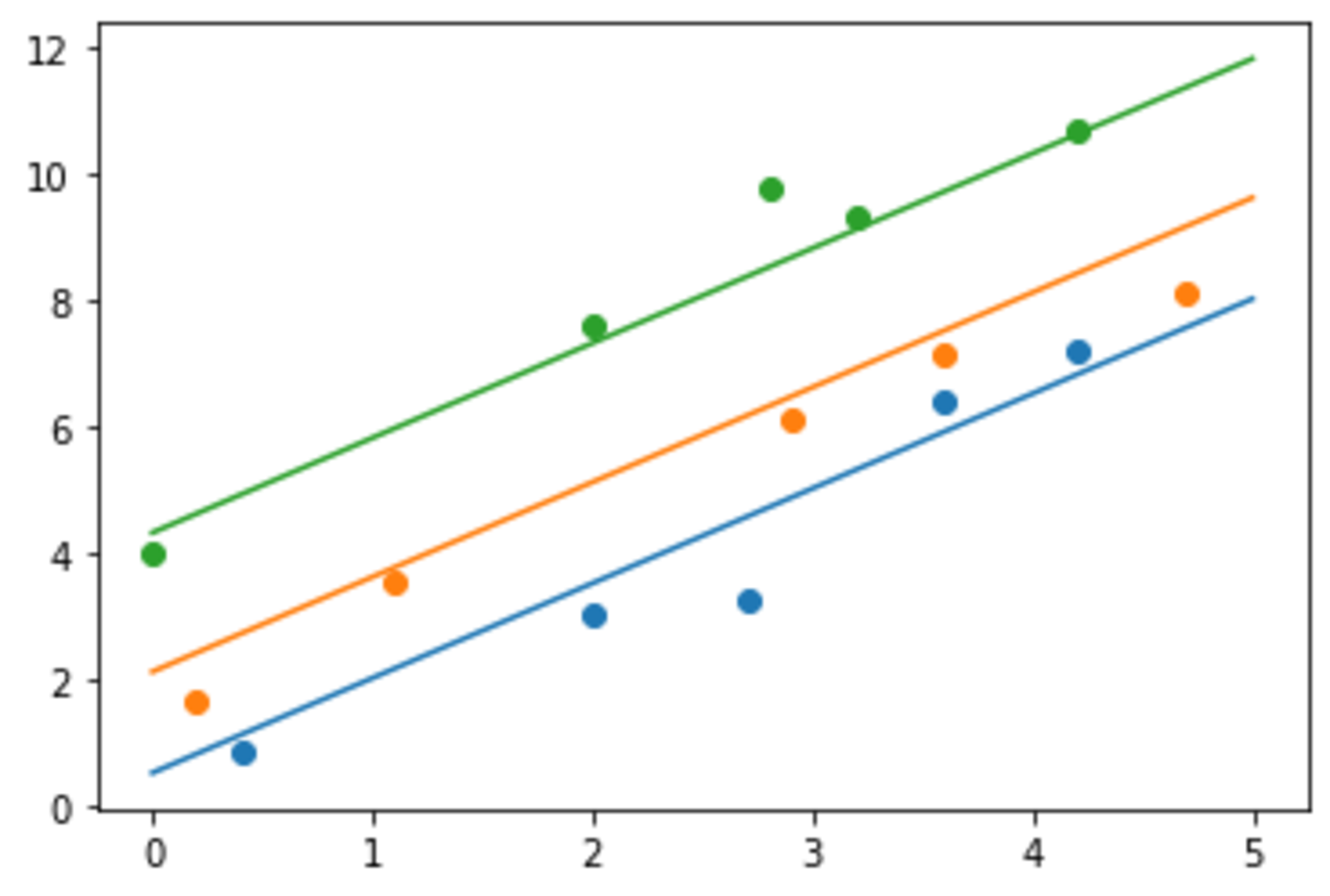プロット

      import numpy as np
np.random.seed(42)

a = 1.5
b1 = 0.5
b2 = 2.1
b3 = 4.3
s = 0.5

x1 = [0.4, 2.0, 2.7, 3.6, 4.2]
x2 = [0.2, 1.1, 2.9, 3.6, 4.7]
x3 = [0.0, 2.0, 2.8, 3.2, 4.2]

y1 = [a*x+b1+np.random.normal(0,s) for x in x1]
y2 = [a*x+b2+np.random.normal(0,s) for x in x2]
y3 = [a*x+b3+np.random.normal(0,s) for x in x3]

X = np.array([x1,x2,x3])
Y = np.array([y1,y2,y3])
    

$x, y$の列をスタックしたものをX,Yとすると，大きさ$M\times N$の行列となります．
単に+，*で演算すると成分ごとの演算となり，$\mean\bullet$,$\B\bullet$は第2成分，第1成分についての平均なので.mean(axis=1),.mean()(注：0-indexed)で得られるため，$a, (b_k)$の推定値は以下のようにそれぞれ1行を求められます．

      a_hat = ((X*Y).mean(axis=1)-X.mean(axis=1)*Y.mean(axis=1)).mean() / ((X**2).mean(axis=1) - X.mean(axis=1)**2).mean()
# => 1.574510913222147
b_hat = Y.mean(axis=1) - a_hat*X.mean(axis=1)
# => array([0.07364212, 1.35999338, 4.42261194])
    

点が少ないのでブレがありますが，一応それらしい値が得られました．

ところでこの解析は，モデルとして階層的なものを最尤推定で求めているため，パラメータ推定として不適切です．
現に，「それっぽい値が出ている」ということしかわからず，推定値がどれくらいの分散を持っているのかすら求められていませんね．
本当はパラメータの分布をベイズ推定で求め，詳しく解析する必要があります．
が，計算が大変なのでそれはまた別の機会に……