エンタメ解説

零数列による級数の加速

級数,加速級数,零数列

あいさつ

んちゃ！

零集合
Euler-Maclaurin展開
零数列の構成
Stirlingの公式
応用1
超幾何関数に関する公式
応用2
最後に

表記

$N_{0} : = {0} \cup N$
$Z e r o ({a_{n}}_{n \in N_{0}}) : = {{w_{n}}_{n \in N_{0}} \subset C | \sum_{n \in N_{0}} w_{n} a_{n} = 0}$
$lim_{N \to \infty} S_{N} ({a_{n}}_{n \in N_{0}}) = S ({a_{n}}_{n \in N_{0}})$

零集合

数列 ${a_{n}}_{n \in N_{0}} \subset C$ に対して定まる以下の様な数列の集合を零集合と呼ぶ。またその元を零数列と呼ぶ。
$Z e r o ({a_{n}}_{n \in N_{0}}) : = {{w_{n}}_{n \in N_{0}} \subset C | \sum_{n \in N_{0}} w_{n} a_{n} = 0}$

零集合 $Z e r o ({a_{n}}_{n \in N_{0}})$ に次の様な和、スカラー積を導入すると零集合はベクトル空間を成す。
$\begin{array}{r} {\begin{cases} 和： \forall {w_{n}}_{n \in N_{0}}, {\overset{―}{w}}_{n \in N_{0}} \in Z e r o ({a_{n}}_{n \in N_{0}}) : {w_{n}}_{n \in N_{0}} + {\overset{―}{w}}_{n \in N_{0}} = {w_{n} + {\overset{―}{w}}_{n}}_{n \in N_{0}} \\ スカラー積： \forall c \in C : \forall {w_{n}}_{n \in N_{0}} \in Z e r o ({a_{n}}_{n \in N_{0}}) : c {w_{n}}_{n \in N_{0}} = {c w_{n}}_{n \in N_{0}} \end{cases} \end{array}$

[0]和、スカラー倍は閉じている。
$\begin{array}{rcl} \forall {w_{n}}_{n \in N_{0}}, {\overset{―}{w}}_{n \in N_{0}} \in Z e r o ({a_{n}}_{n \in N_{0}}) : \sum_{n = 0}^{\infty} (w_{n} + {\overset{―}{w}}_{n}) a_{n} & = & \sum_{n = 0}^{\infty} w_{n} a_{n} + \sum_{n = 0}^{\infty} {\overset{―}{w}}_{n} a_{n} \\ = & 0 + 0 \\ = & 0 \end{array}$
また
$\begin{array}{rcl} \forall c \in C : \forall {w_{n}}_{n \in N_{0}} \in Z e r o ({a_{n}}_{n \in N_{0}}) : \sum_{n = 0}^{\infty} (c w_{n}) a_{n} & = & c \sum_{n = 0}^{\infty} w_{n} a_{n} \\ = & c 0 \\ = & 0 \end{array}$
[1]結合法則
$\begin{array}{rcl} \forall {w_{n}}_{n \in N_{0}}, {\overset{―}{w}}_{n \in N_{0}}, {\overset{―}{\overset{―}{w}}}_{n \in N_{0}} \in Z e r o ({a_{n}}_{n \in N_{0}}) : \sum_{n = 0}^{\infty} (w_{n} + ({\overset{―}{w}}_{n} + {\overset{―}{\overset{―}{w}}}_{n})) a_{n} & = & \sum_{n = 0}^{\infty} ((w_{n} + {\overset{―}{w}}_{n}) + {\overset{―}{\overset{―}{w}}}_{n}) a_{n} \end{array}$
[2]単位元： ${0} \in Z e r o ({a_{n}}_{n \in N_{0}})$
$\begin{array}{rcl} \forall {w_{n}}_{n \in N_{0}} \in Z e r o ({a_{n}}_{n \in N_{0}}) : \sum_{n = 0}^{\infty} (w_{n} + 0) a_{n} & = & \sum_{n = 0}^{\infty} (0 + w_{n}) a_{n} \\ = & \sum_{n = 0}^{\infty} w_{n} a_{n} \end{array}$
[3]逆元： ${- w_{n}}_{n \in N_{0}} \in Z e r o ({a_{n}}_{n \in N_{0}})$
$\begin{array}{rcl} \forall {w_{n}}_{n \in N_{0}} \in Z e r o ({a_{n}}_{n \in N_{0}}) : \sum_{n = 0}^{\infty} (w_{n} + (- w_{n})) a_{n} & = & \sum_{n = 0}^{\infty} (- w_{n} + w_{n}) a_{n} \\ = & \sum_{n = 0}^{\infty} 0 a_{n} \\ = & 0 \end{array}$
[4]可換性
$\begin{array}{rcl} \forall {w_{n}}_{n \in N_{0}}, {\overset{―}{w}}_{n \in N_{0}} \in Z e r o ({a_{n}}_{n \in N_{0}}) : \sum_{n = 0}^{\infty} (w_{n} + {\overset{―}{w}}_{n}) a_{n} & = & \sum_{n = 0}^{\infty} ({\overset{―}{w}}_{n} + w_{n}) a_{n} \end{array}$
[5]ベクトルに関する分配法則
$\begin{array}{r} \forall c \in C : \forall {w_{n}}_{n \in N_{0}}, {\overset{―}{w}}_{n \in N_{0}} \in Z e r o ({a_{n}}_{n \in N_{0}}) : \sum_{n = 0}^{\infty} (c (w_{n} + {\overset{―}{w}}_{n})) a_{n} = \sum_{n = 0}^{\infty} (c w_{n} + c {\overset{―}{w}}_{n}) a_{n} \end{array}$
[6]スカラーに関する分配法則
$\begin{array}{r} \forall c, d \in C : \forall {w_{n}}_{n \in N_{0}} \in Z e r o ({a_{n}}_{n \in N_{0}}) : \sum_{n = 0}^{\infty} ((c + d) w_{n}) a_{n} = \sum_{n = 0}^{\infty} (c w_{n} + d w_{n}) a_{n} \end{array}$
[7]スカラー積に関する結合法則
$\forall c, d \in C : \forall {w_{n}}_{n \in N_{0}} \in Z e r o ({a_{n}}_{n \in N_{0}}) : \sum_{n = 0}^{\infty} ((c d) w_{n}) a_{n} = \sum_{n = 0}^{\infty} (c (d w_{n})) a_{n}$
[8]スカラー積の単位元： $1 \in C$
$\begin{array}{r} \forall {w_{n}}_{n \in N_{0}} \in Z e r o ({a_{n}}_{n \in N_{0}}) : \sum_{n = 0}^{\infty} (1 w_{n}) a_{n} = \sum_{n = 0}^{\infty} w_{n} a_{n} \end{array}$

数列 ${a_{n}}_{n \in N_{0}} \subset C$ に対して定まる総和 $S ({a_{n}}_{n \in N_{0}}) : = \sum_{n = 0}^{\infty} a_{n}$ は下記の性質を持つ。
$\forall {w_{n}}_{n \in N_{0}} \in Z e r o ({a_{n}}_{n \in N_{0}}) : S ({a_{n}}_{n \in N_{0}}) = \sum_{n = 0}^{\infty} (1 + w_{n}) a_{n}$

そのまま計算するだけ。
$\begin{array}{rcl} \sum_{n = 0}^{\infty} (1 + w_{n}) a_{n} & = & \sum_{n = 0}^{\infty} a_{n} + \sum_{n = 0}^{\infty} w_{n} a_{n} \\ = & S ({a_{n}}_{n \in N_{0}}) + 0 \\ = & S ({a_{n}}_{n \in N_{0}}) \end{array}$

D

次の加速度を持つ零数列

数列 ${a_{n}}_{n \in N_{0}}$ に対して定まる総和 $S_{N} ({a_{n}}_{n \in N_{0}}) : = \sum_{n = 0}^{N - 1} a_{n}$ に対して次の性質を満たす数列 ${w_{n}}_{n \in N_{0}} \in Z e r o ({a_{n}}_{n \in N_{0}})$ を $D$ 次の加速度を持つ零数列と呼ぶ。
$\exists A \in R_{+} s . t . | S_{N} ({a_{n}}_{n \in N_{0}}) - \sum_{n = 0}^{N - 1} w_{n} a_{n} - S ({a_{n}}_{n \in N_{0}}) | < \frac{A}{N^{D}}$

漸近表示

数列 ${a_{n}}_{n \in N_{0}}$ に対して定まる総和 $S_{N} ({a_{n}}_{n \in N_{0}}) : = \sum_{n = 0}^{N - 1} a_{n}$ に対して定まる次の性質を満たす $N$ に関する多項式が存在する時、 $D$ 次の漸近表示と呼ぶ。
$\exists A_{0}, A_{1}, . . ., A_{D - 1} s . t . S_{N} ({a_{n}}_{n \in N_{0}}) = S ({a_{n}}_{n \in N_{0}}) + \sum_{n = 0}^{D - 1} A_{n} N^{n} + O (N^{D})$

Euler-Maclaurin展開

Euler-Maclaulinの和公式導出

やりたい事: $S_{m n} = \sum_{k = m}^{n} f (k)$ を積分で近似したい。

Euler-Maclaurinの公式

[1]まずはとりあえず、総和と積分の差分でも計算してみましょう。

\begin{array}{rcl} ϵ_{m n} & = & S_{m n} - f (n) - \int_{m}^{n} f (x) d x \\ = & \sum_{k = m}^{n - 1} f (k) - \sum_{k = m}^{n - 1} \int_{k}^{k + 1} f (x) d x \\ = & \sum_{k = m}^{n - 1} {f (k) - \int_{0}^{1} f (x + k) d x} \end{array}

[2]区間

[0, 1]

で定義された微分可能な関数

ψ (x)

を考えて次の条件が成り立つ場合を考えてみる。

\begin{array}{rcl} \int_{0}^{1} ψ (x) f^{^{'}} (x + k) d x & = & ψ (1) f (k + 1) - ψ (0) f (k) - \int_{0}^{1} ψ^{^{'}} (x) f (x + k) d x (- ψ (0) = ψ (1) = \frac{1}{2}, ψ^{^{'}} (x) = 1 \Rightarrow ψ (x) = x - \frac{1}{2}) \\ = & \frac{1}{2} {f (k) + f (k + 1)} - \int_{0}^{1} f (x + k) d x \end{array}

この事を用いると。望遠鏡和を使う事で下記の式を得る。

\begin{array}{r} {\begin{cases} ψ (x) = x - \frac{1}{2} \\ - \frac{f (n) - f (m)}{2} + \sum_{k = m}^{n - 1} \int_{0}^{1} ψ (x) f^{^{'}} (x + k) d x = S_{m n} - f (n) - \int_{m}^{n} f (x) d x \end{cases} \end{array}

[3]次に以下の様な記号を定めてみよう。

\begin{array}{r} {\begin{cases} R_{m n}^{N} = \sum_{k = m}^{n - 1} \int_{0}^{1} B_{N} (x) f^{(N)} (x + k) (N = 1, 2, . . .) \\ B_{N}^{^{'}} (x) = B_{N - 1} (x) (N = 2, 3, . . .) \\ B_{N} (0) = B_{N} (1) = b_{N - 1} (N = 2, 3, . . .) \\ B_{1} (x) = ψ (x) \end{cases} \end{array}

R_{m n}^{(N - 1)}, R_{m n}^{N}

との間に成り立つ関係式

\begin{array}{rcl} R_{m n}^{N} & = & \sum_{k = m}^{n - 1} \int_{0}^{1} B_{N} (x) f^{(N)} (x + k) \\ = & \sum_{k = m}^{n - 1} [B_{N} (x) f^{(N - 1)} (x + k)]_{0}^{1} - \int_{0}^{1} B_{N}^{^{'}} (x) f^{(N - 1)} (x) d x \\ = & b_{N - 1} {f^{(N - 1)} (n) - f^{(N - 1)} (m)} - \int_{0}^{1} B_{N - 1} (x) f^{(N - 1)} (x) d x \\ = & b_{N - 1} {f^{(N - 1)} (n) - f^{(N - 1)} (m)} - R_{m n}^{(N - 1)} \\ = & b_{N - 1} {f^{(N - 1)} (n) - f^{(N - 1)} (m)} - b_{N - 2} {f^{(N - 2)} (n) - f^{(N - 2)} (m)} + \dots + (- 1)^{N - 2} b_{1} {f^{(1)} (n) - f^{(1)} (m)} + (- 1)^{N - 1} R_{m n}^{1} \end{array}

以上の計算から

\begin{array}{rcl} R_{m n}^{1} & = & (- 1)^{N} b_{N - 1} {f^{(N - 1)} (n) - f^{(N - 1)} (m)} + (- 1)^{N - 1} b_{N - 2} {f^{(N - 2)} (n) - f^{(N - 2)} (m)} + \dots + b_{1} {f^{(1)} (n) - f^{(1)} (m)} + (- 1)^{N - 1} R_{m n}^{N} \\ = & \sum_{k = 1}^{N - 1} (- 1)^{k + 1} b_{k} {f^{k} (n) - f^{(k)} (m)} + (- 1)^{N - 1} R_{m n}^{N} \end{array}

B_{N} (x)

を具体的に求める。
(i)まず次のような母関数

f (x, y) = 1 + \sum_{N = 1}^{\infty} B_{N} (x) y^{N}

を定める。
(ii)両辺を

x

で偏微分する。

\begin{array}{rcl} \frac{\partial}{\partial x} f (x, y) & = & \sum_{N = 1}^{\infty} B_{N}^{^{'}} (x) y^{N} \\ = & y {1 + \sum_{N = 2}^{\infty} B_{N - 1} (x) y^{N - 1}} \\ = & y {1 + \sum_{N = 1}^{\infty} B_{N} (x) y^{n}} \\ = & y f (x, y) \end{array}

この計算から、ある

y

に関する関数を用いて以下の結果を得る。

\begin{array}{r} f (x, y) = g (y) e^{y x} \end{array}

(iii)さらに

\begin{array}{r} {\begin{cases} f (0, y) = 1 - \frac{1}{2} y + \sum_{N = 2}^{\infty} b_{N - 1} y^{N} \\ f (1, y) = 1 + \frac{1}{2} y + \sum_{N = 2}^{\infty} b_{N - 1} y^{N} \end{cases} \end{array}

を用いると次式が得られる。

g (y) + \frac{1}{2} y = g (y) e^{y} - \frac{1}{2} y

この式を用いる事で下記の式を得る。

g (y) = \frac{y}{e^{y} - 1}

(iv)以上の結果をまとめる事で

f (x, y) = \frac{y e^{x y}}{e^{y} - 1}

(v)また以上の計算により

{b_{N}}

の母関数は下記の様に書ける事が分かる。

f (1, y) = \frac{y}{1 - e^{- y}} = 1 + \frac{1}{2} y + \sum_{N = 2}^{\infty} b_{N - 1} y^{N}

[4]

{b_{N}}

の満たす漸化式を求める。

\begin{array}{rcl} y & = & (1 + \frac{1}{2} y + \sum_{N = 2}^{\infty} b_{N - 1} y^{N}) (1 - e^{- y}) \\ = & (\sum_{M = 1}^{\infty} \frac{(- 1)^{M}}{M!} y^{M}) (1 + \frac{1}{2} y + \sum_{N = 2}^{\infty} b_{N - 1} y^{N}) (1 + \frac{1}{2} y + \sum_{N = 2}^{\infty} b_{N - 1} y^{N} = \sum_{N = 0}^{\infty} c_{N} y^{N}) \\ = & \sum_{M = 1}^{\infty} \sum_{N = 0}^{\infty} \frac{(- 1)^{M - 1}}{M!} c_{N} y^{M + N} (M + N = L) \\ = & \sum_{L = 1}^{\infty} \sum_{M = 1}^{L} \frac{(- 1)^{M - 1}}{M!} c_{L - M} y^{L} \end{array}

係数比較により下記の漸化式を得る。

\begin{array}{rcl} \sum_{M = 1}^{N} \frac{(- 1)^{M - 1}}{M!} c_{N - M} & = & \frac{(- 1)^{N - 1}}{N!} + \frac{(- 1)^{N - 2}}{2 (N - 1)!} + \sum_{M = 1}^{N - 2} \frac{(- 1)^{M - 1}}{M!} b_{N - M - 1} \\ = & \sum_{M = 1}^{N - 2} \frac{(- 1)^{N - M}}{{N - (M + 1)}!} b_{M} + \frac{(- 1)^{N - 2}}{2 (N - 1)!} + \frac{(- 1)^{N - 1}}{N!} \\ = & 0 \end{array}

[5]

b_{2 n} \dots = 0 (n \in N)

を確認する。

\begin{array}{rcl} f (1, y) - \frac{1}{2} y & = & y \frac{1 + e^{- y}}{2 (1 - e^{- y})} \\ = & y \frac{\cosh \frac{y}{2}}{\sinh \frac{y}{2}} \end{array}

この関数は遇関数なので

y^{2 n + 1}

の係数は

0

なので[5]の結果が得られる。

[6]

b_{1}, b_{3}, b_{5}

を試しに計算してみよう。
(i)

b_{1} (N = 3)

について

\begin{array}{rcl} b_{1} - \frac{1}{4} + \frac{1}{6} & = & b_{1} - \frac{1}{2} (\frac{1}{2} - \frac{1}{3}) \\ = & b_{1} - \frac{1}{12} \\ = & 0 \Rightarrow b_{1} = \frac{1}{12} \end{array}

(ii)

b_{3} (N = 5)

について

\begin{array}{rcl} b_{3} + \frac{1}{6} b_{1} - \frac{1}{48} + \frac{1}{120} & = & b_{3} + \frac{1}{12} (\frac{1}{6} - \frac{1}{4} + \frac{1}{10}) \\ = & b_{3} + \frac{1}{12} (- \frac{1}{12} + \frac{1}{10}) \\ = & b_{3} + \frac{1}{24} (- \frac{1}{6} + \frac{1}{5}) \\ = & b_{3} + \frac{1}{24} \frac{1}{30} \\ = & b_{3} + \frac{1}{720} \\ = & 0 \Rightarrow b_{3} = - \frac{1}{720} \end{array}

(iii)

b_{5} (N = 7)

について

\begin{array}{rcl} b_{5} + \frac{1}{6} b_{3} + \frac{1}{120} b_{1} - \frac{1}{1440} + \frac{1}{5040} & = & b_{5} - \frac{1}{4320} + \frac{1}{1440} - \frac{1}{1440} + \frac{1}{5040} \\ = & b_{5} - \frac{1}{4320} + \frac{1}{5040} \\ = & b_{5} + \frac{1}{720} (- \frac{1}{6} + \frac{1}{7}) \\ = & b_{5} - \frac{1}{720 \cdot 42} \\ = & b_{5} - \frac{1}{30240} \\ = & 0 \Rightarrow b_{5} = \frac{1}{30240} \end{array}

を得る。

[6]上記をまとめると

\sum_{k = m}^{n} f (k) = \int_{m}^{n} f (x) d x + \frac{f (m) + f (n)}{2} + \frac{f^{(1)} (n) - f^{(1)} (m)}{12} - \frac{f^{(3)} (n) - f^{(3)} (m)}{720} + \frac{f^{(5)} (n) - f^{(5)} (m)}{30240} + R_{m n}^{7}

零数列の構成

零数列の構成法

[1]数列

{a_{n}}_{n \in N_{0}}

に対して定まる総和

S_{N} ({a_{n}}_{n \in N_{0}})

のEuler-Maclaurin展開を求める。

S_{N} ({a_{n}}_{n \in N_{0}}) = S ({a_{n}}_{n \in N_{0}}) + \sum_{n = 1}^{D - 1} \frac{A_{n}}{N^{n}} + O (\frac{1}{N^{D}})

[2]二重級数

{f_{n m}}_{n, m \in N_{0}}

から以下の様な数列

{w_{n}}_{n \in N_{0}}

を構成する。

w_{n} = \sum_{m = 0}^{D - 2} f_{n, m} B_{m}

[3]次に、

\sum_{n = 0}^{N - 1} w_{n} a_{n} = δ + \sum_{n = 1}^{D - 1} \frac{A_{n}}{N^{n}} + O (\frac{1}{N^{D}})

を満たすように漸近展開を行う。
[4]最終的に

a_{n} \neq 0

を満たす最小の

n_{0}

を求めて

w_{n_{0}} \leftarrow w_{n_{0}} - \frac{δ}{a_{n_{0}}}

とすれば

{w_{n}}_{n \in N_{0}}

は

D

次の加速度を持つ零数列になる。

Stirlingの公式

Wallisの公式

$π = lim_{n \to \infty} \frac{2^{2 n} (n!)^{4}}{n {(2 n)!}^{2}}$

[0] $I_{n} : = \int_{0}^{\frac{π}{2}} \sin^{n} x d x$ とおく。
[1]すると $I_{n}$ は $n$ に関して単調減少。なぜなら、 $\forall x \in (0, 1) : \sin x \in (0, 1)$ なので $\forall n \in N_{0} : \forall x \in (0, 1) : 0 < \sin^{n + 1} x < \sin^{n} x$ 。
ゆえに、 $0 < I_{n + 1} < I_{n}$
[2]下記の様に計算ができる
$\begin{array}{rcl} I_{n} & = & \int_{0}^{\frac{π}{2}} \sin^{n} x d x \\ = & - \sin^{n - 1} x \cos x |_{0}^{\frac{π}{2}} + (n - 1) \int_{0}^{\frac{π}{2}} \sin^{n - 2} x \cos^{2} x d x \\ = & (n - 1) I_{n - 2} - (n - 1) I_{n} \end{array}$
$I_{n} = \frac{n - 1}{n} I_{n - 2}$
[3][2]を用いると以下の結果を得る。
$\begin{array}{r} {\begin{cases} I_{2 n} = \frac{2 n - 1}{2 n} \frac{2 n - 3}{2 n - 2} \dots \frac{1}{2} \frac{π}{2} = \frac{(2 n)!}{2^{2 n} (n!)^{2}} \frac{π}{2} \\ I_{2 n + 1} = \frac{2 n}{2 n + 1} \frac{2 n - 2}{2 n - 1} \dots \frac{2}{3} = \frac{2^{2 n} (n!)^{2}}{(2 n + 1)!} \end{cases} \end{array}$
[4][1]より $I_{2 n + 1} < I_{2 n} < I_{2 n - 1}$ とする。すると下記の様に計算できる。
$\begin{array}{r} 1 < \frac{I_{2 n}}{I_{2 n - 1}} = n {\frac{(2 n)!}{2^{2 n} (n!)^{2}}}^{2} π < \frac{1}{1 + \frac{1}{2 n}} \end{array}$
[5]
$π = lim_{n \to \infty} \frac{2^{2 n} (n!)^{4}}{n {(2 n)!}^{2}}$

Stirlingの公式

$N! ≃ \frac{\sqrt{2 π N} N^{N}}{e^{N}} + e^{O (\frac{1}{N})}$

[1]Euler-Maclaurin展開より下記の様に計算できる。
$\begin{array}{rcl} \log N! & = & \sum_{n = 0}^{N - 1} \log (n + 1) \\ = & \int_{0}^{N - 1} \log (x + 1) d x + \frac{\log N}{2} + \frac{\frac{1}{N} - 1}{12} + \dots \\ = & \log C + N \log N - N + \frac{\log N}{2} + O (\frac{1}{N}) \\ = & \log (C N^{N + \frac{1}{2}} e^{- N}) + O (\frac{1}{N}) \end{array}$
[2]上記の計算により
$C = lim_{n \to \infty} \frac{N! e^{N}}{N^{N + \frac{1}{2}}}$
[3]定数 $C$ についてはWallisの公式より下記の様に計算できる。
$\begin{array}{rcl} \sqrt{π} & = & lim_{n \to \infty} \frac{2^{2 n} (n!)^{2}}{n^{\frac{1}{2}} {(2 n)!}} \\ = & \frac{1}{\sqrt{2}} lim_{n \to \infty} \frac{n! e^{n}}{n^{n + \frac{1}{2}}} \frac{n! e^{n}}{n^{n + \frac{1}{2}}} \frac{(2 n)^{2 n + \frac{1}{2}}}{(2 n)!} \\ = & \frac{C}{\sqrt{2}} \end{array}$
[4]ゆえに $C = \sqrt{2 π}$ が得られるので、最終的に以下の式が証明された。
$N! = \frac{\sqrt{2 π N} N^{N}}{e^{N}} + e^{O (\frac{1}{N})}$

中央二項係数に関するStirlingの公式

$(\begin{matrix} 2 n \\ n \end{matrix}) ≃ \frac{4^{n}}{\sqrt{π n}}$

$\begin{array}{rcl} (\begin{array}{c} 2 n \\ n \end{array}) & = & \frac{(2 n)!}{n! n!} \\ = & \frac{\sqrt{4 π n} (2 n)^{2 n}}{e^{2 n}} \frac{e^{n}}{\sqrt{2 π n} n^{n}} \frac{e^{n}}{\sqrt{2 π n} n^{n}} \\ = & \frac{4^{n}}{\sqrt{π n}} \end{array}$

応用1

[1]まず以下の様に二重数列を置いてみます。
$\begin{array}{r} f_{n m} = 256^{n} \frac{A_{m} (n + 1)^{m}}{(n + 1)^{4} {(\begin{array}{c} 2 (n + 1) \\ n + 1 \end{array})}^{4}} \end{array}$
[2]
$\begin{array}{rcl} w_{n} & = & 256^{n + 1} \frac{A_{2} (n + 1)^{2} + A_{1} (n + 1) + A_{0}}{(n + 1)^{4} {(\begin{array}{c} 2 (n + 1) \\ n + 1 \end{array})}^{4}} \end{array}$
[3]Stirlingの公式を用いると十分大きな $N$ に対して下記の様に書ける。
$\begin{array}{rcl} \sum_{n = 0}^{N - 1} \frac{w_{n}}{(n + 1)^{2}} & = & \sum_{n = 0}^{N - 1} 256^{n + 1} \frac{A_{2} (n + 1)^{2} + A_{1} (n + 1) + A_{0}}{(n + 1)^{6} {(\begin{array}{c} 2 (n + 1) \\ n + 1 \end{array})}^{4}} \\ ≃ & \sum_{n = 0}^{N - 1} 256^{n + 1} \frac{A_{2} (n + 1)^{2} + A_{1} (n + 1) + A_{0}}{(n + 1)^{6} (\frac{4^{n + 1}}{\sqrt{π (n + 1)}})^{4}} \\ = & π^{2} \sum_{n = 0}^{N - 1} \frac{A_{2} (n + 1)^{2} + A_{1} (n + 1) + A_{0}}{(n + 1)^{4}} \\ = & A_{2} π^{2} \sum_{n = 0}^{N - 1} \frac{1}{(n + 1)^{2}} + A_{1} π^{2} \sum_{n = 0}^{N - 1} \frac{1}{(n + 1)^{3}} + A_{0} π^{2} \sum_{n = 0}^{N - 1} \frac{1}{(n + 1)^{4}} \end{array}$
[4]そこで、以下の様に記号を定める $f_{k} (x) = \frac{1}{(x + 1)^{4 - k}}$
$\begin{array}{r} f^{(n)} (x) = (- 1)^{n} \frac{(4 - k)_{n}}{(x + 1)^{4 - k + n}} \end{array}$
ゆえに
$\begin{array}{r} \sum_{n = 0}^{N - 1} \frac{1}{(n + 1)^{4 - k}} = ζ (4 - k) - \frac{1}{(3 - k) N^{3 - k}} + \frac{1}{2 N^{4 - k}} - \frac{4 - k}{12 N^{5 - k}} + O (\frac{1}{N^{7 - k}}) (k = 0, 1, 2) \end{array}$
[5][3][4]より次の様に計算できる。
$\begin{array}{rcl} \sum_{n = 0}^{N - 1} \frac{w_{n}}{(n + 1)^{2}} & = & A_{2} π^{2} ζ (2) + A_{1} π^{2} ζ (3) + A_{0} π^{2} ζ (4) \\ - & \frac{A_{2} π^{2}}{N} \\ + & (\frac{A_{2} π^{2}}{2} - \frac{A_{1} π^{2}}{2}) \frac{1}{N^{2}} + O (\frac{1}{N^{3}}) \end{array}$
[6][5]より
$\begin{array}{r} {\begin{cases} A_{2} = \frac{1}{π^{2}} \\ A_{1} = 0 \\ A_{0} = - \frac{ζ (2)}{π^{2} ζ (4)} \end{cases} \end{array}$
ゆえに $4$ 次の加速度を持つ数列は下記の様に書ける。
$\sum_{n = 0}^{\infty} 256^{n + 1} \frac{π^{2} (n + 1)^{2} - 15}{π^{4} (n + 1)^{6} {(\begin{matrix} 2 (n + 1) \\ n + 1 \end{matrix})}^{4}} = δ = - 0.243004 \dots$
👆 $\sum_{n = 0}^{N - 1} 256^{n + 1} \frac{π^{2} (n + 1)^{2} - 15}{π^{4} (n + 1)^{6} {(\begin{matrix} 2 (n + 1) \\ n + 1 \end{matrix})}^{4}} + 1 / N - \frac{1}{2 N^{2}} = δ + O (\frac{1}{N^{3}})$ により計算しています。
この問題を完全に解くには上記級数の真の値を求めないといけません。
$\begin{array}{r} {\begin{cases} w_{0} = \frac{16 π^{2} - 240}{π^{4}} - δ \\ w_{n} = 256^{n + 1} \frac{π^{2} (n + 1)^{2} - 15}{π^{4} (n + 1)^{4} {(\begin{array}{c} 2 (n + 1) \\ n + 1 \end{array})}^{4}} \end{cases} \end{array}$

$\begin{array}{r} \exists δ \in R s . t . 1 - \frac{16 π^{2} - 240}{π^{4}} + δ + \sum_{n = 2}^{N} {1 - 256^{n} \frac{π^{2} n^{2} - 15}{π^{4} n^{4} {(\begin{array}{c} 2 n \\ n \end{array})}^{4}}} \frac{1}{n^{2}} = ζ (2) + O (\frac{1}{N^{3}}) \end{array}$
因みに $δ$ は次の様に書ける。
$δ : = \sum_{n = 1}^{\infty} 256^{n} \frac{π^{2} n^{2} - 15}{π^{4} n^{6} {(\begin{matrix} 2 n \\ n \end{matrix})}^{4}}$

超幾何関数に関する公式

中央二項係数の逆数のべきを含む和による級数ってかっこいいですよね？
この様な級数をガンマ関数や対数関数などを使ってビシッと答えれてたらキターンって感じです！
ではその様な計算が出来るよう公式を作成しましょう。

下記の様な $p, q \in N_{0} (p \leq q)$ によって定まる級数 $S (p, q) : = \sum_{n = 1}^{\infty} \frac{1}{n^{p} {(\begin{matrix} 2 n \\ n \end{matrix})}^{q}}$ は超幾何関数により次の様に書ける。
$S (p, q) = \frac{1}{2^{q}}_{q + 1} F_{q} ({1}^{p + 1}, {2}^{q - p}; {\frac{3}{2}}^{q}; \frac{1}{4^{q}})$

[1] $t_{n} : = \frac{1}{n^{p} {(\begin{matrix} 2 n \\ n \end{matrix})}^{q}}$ とおく。
[2] $t_{n}$ は超幾何項。
$\begin{array}{rcl} \frac{t_{n + 1}}{t_{n}} & = & \frac{n^{p} {(\begin{array}{c} 2 n \\ n \end{array})}^{q}}{(n + 1)^{p} {(\begin{array}{c} 2 n + 2 \\ n + 1 \end{array})}^{q}} \\ = & \frac{n^{p} (n + 1)^{2 q}}{(n + 1)^{p} (2 n + 2)^{q} (2 n + 1)^{q}} \\ = & \frac{n^{p} (n + 1)^{q - p}}{2^{q} (2 n + 1)^{q}} \\ = & \frac{n^{p} (n + 1)^{q - p}}{2^{2 q + 1} (n + \frac{1}{2})^{q}} \end{array}$
[3]ゆえに
$\begin{array}{rcl} t_{n} & = & \frac{(n - 1)^{p} n^{q - p}}{2^{2 q + 1} (n - \frac{1}{2})^{q}} t_{n - 1} \\ = & \frac{(1)_{n - 1}^{p} (2)_{n - 1}^{q - p}}{2^{2 q (n - 1)} (\frac{3}{2})_{n - 1}^{q}} t_{1} \\ = & \frac{(1)_{n - 1}^{p} (2)_{n - 1}^{q - p}}{2^{q (2 n - 1)} (\frac{3}{2})_{n - 1}^{q}} \end{array}$
[4]以上の事を代入すると
$\begin{array}{rcl} S (p, q) & = & \sum_{n = 1}^{\infty} t_{n} \\ = & \sum_{n = 0}^{\infty} \frac{(1)_{n}^{p} (2)_{n}^{q - p}}{2^{q (2 n + 1)} (\frac{3}{2})_{n}^{q}} \\ = & \frac{1}{2^{q}} \sum_{n = 0}^{\infty} \frac{(1)_{n}^{p + 1} (2)_{n}^{q - p}}{(\frac{3}{2})_{n}^{q}} \frac{1}{n! 4^{q n}} \\ = & \frac{1}{2^{q}}_{q + 1} F_{q} ({1}^{p + 1}, {2}^{q - p}; {\frac{3}{2}}^{q}; \frac{1}{4^{q}}) \end{array}$

$\begin{array}{r} \forall n \in N_{0} : \forall a \in C : {\begin{cases} (a)_{2 n} = 2^{2 n} (\frac{a}{2})_{n} (\frac{a + 1}{2})_{n} \\ (a)_{2 n + 1} = 2^{2 n} a (\frac{a + 1}{2})_{n} (\frac{a}{2} + 1)_{n} \end{cases} \end{array}$

実際に計算すればよい。
$\begin{array}{rcl} (a)_{2 n} & = & a (a + 1) (a + 2) \dots (a + 2 n - 2) (a + 2 n - 1) \\ = & a (a + 2) (a + 4) \dots (a + 2 n - 2) (a + 1) (a + 3) \dots (a + 2 n - 1) \\ = & 2^{2 n} \frac{a}{2} (\frac{a}{2} + 1) (\frac{a}{2} + 2) \dots (\frac{a}{2} + n - 1) (\frac{a}{2} + \frac{1}{2}) (\frac{a}{2} + \frac{1}{2} + 1) \dots (\frac{a}{2} + \frac{1}{2} + n - 1) \\ = & 2^{2 n} (\frac{a}{2})_{n} (\frac{a + 1}{2})_{n} \end{array}$
$\begin{array}{r} (a)_{2 n + 1} = 2^{2 n} a (\frac{a + 1}{2})_{n} (\frac{a}{2} + 1)_{n} \end{array}$

$\begin{array}{r} \forall n \in N_{0} : \forall a \in C : {\begin{cases} (a)_{3 n} = 3^{3 n} (\frac{a}{3})_{n} (\frac{a + 1}{3})_{n} (\frac{a + 2}{3})_{n} \\ (a)_{3 n + 1} = 3^{n} a (\frac{a + 1}{3})_{n} (\frac{a + 2}{3})_{n} (\frac{a}{3} + 1)_{n} \\ (a)_{3 n + 2} = 3^{n} a (a + 1) (\frac{a + 2}{3})_{n} (\frac{a}{3} + 1)_{n} (\frac{a + 1}{3} + 1)_{n} \end{cases} \end{array}$

これも実際に計算すればいい。
$\begin{array}{rcl} (a)_{3 n} & = & a (a + 3) (a + 6) \dots (a + 3 n - 3) (a + 1) (a + 4) \dots (a + 3 n - 2) (a + 2) (a + 5) \dots (a + 3 n - 1) \\ = & 3^{3 n} \frac{a}{3} (\frac{a}{3} + 1) (\frac{a}{3} + 2) \dots (\frac{a}{3} + n - 1) \frac{a + 1}{3} (\frac{a + 1}{3} + 1) \dots (\frac{a + 1}{n} + n - 1) \frac{a + 2}{3} (\frac{a + 2}{3} + 1) \dots (\frac{a + 2}{3} + n - 1) \\ = & 3^{3 n} (\frac{a}{3})_{n} (\frac{a + 1}{3})_{n} (\frac{a + 2}{3})_{n} \end{array}$
$\begin{array}{r} (a)_{3 n + 1} = 3^{n} a (\frac{a + 1}{3})_{n} (\frac{a + 2}{3})_{n} (\frac{a}{3} + 1)_{n} \end{array}$
$\begin{array}{r} (a)_{3 n + 2} = 3^{n} a (a + 1) (\frac{a + 2}{3})_{n} (\frac{a}{3} + 1)_{n} (\frac{a + 1}{3} + 1)_{n} \end{array}$

$\begin{array}{r} {\begin{cases} _{p} F_{q} (a_{1}, a_{2}, . . ., a_{p}; b_{1}, b_{2}, . . ., b_{q}; z) +_{p} F_{q} (a_{1}, a_{2}, . . ., a_{p}; b_{1}, b_{2}, . . ., b_{q}; - z) = 2_{2 p} F_{2 q + 1} (\frac{a_{1}}{2}, \frac{a_{1} + 1}{2}, \frac{a_{2}}{2}, \frac{a_{2} + 1}{2}, . . ., \frac{a_{p}}{2}, \frac{a_{p} + 1}{2}; \frac{b_{1}}{2}, \frac{b_{1} + 1}{2}, \frac{b_{2}}{2}, \frac{b_{2} + 1}{2}, . . ., \frac{b_{q}}{2}, \frac{b_{q} + 1}{2}, \frac{1}{2}; (2^{p - q - 1} z)^{2}) \\ _{p} F_{q} (a_{1}, a_{2}, . . ., a_{p}; b_{1}, b_{2}, . . ., b_{q}; z) -_{p} F_{q} (a_{1}, a_{2}, . . ., a_{p}; b_{1}, b_{2}, . . ., b_{q}; - z) = 2 \frac{a_{1} a_{2} \dots a_{p}}{b_{1} b_{2} \dots b_{q}} z_{2 p} F_{2 q + 1} (\frac{a_{1} + 1}{2}, \frac{a_{1} + 2}{2}, \frac{a_{2} + 1}{2}, \frac{a_{2} + 2}{2}, . . ., \frac{a_{p} + 1}{2}, \frac{a_{p} + 2}{2}; \frac{b_{1} + 1}{2}, \frac{b_{1} + 2}{2}, \frac{b_{2} + 1}{2}, \frac{b_{2} + 2}{2}, . . ., \frac{b_{q} + 1}{2}, \frac{b_{q} + 2}{2}, \frac{3}{2}; (2^{p - q - 1} z)^{2}) \end{cases} \end{array}$

[1]
$\begin{array}{rcl} _{p} F_{q + 1} (a_{1}, a_{2}, . . ., a_{p}; b_{1}, b_{2}, . . ., b_{q}; z) +_{p} F_{q} (a_{1}, a_{2}, . . ., a_{p}; b_{1}, b_{2}, . . ., b_{q}; - z) & = & 2 \sum_{n = 0}^{\infty} \frac{(a_{1})_{2 n} (a_{2})_{2 n} \dots (a_{p})_{2 n}}{(b_{1})_{2 n} (b_{2})_{2 n} \dots (b_{q})_{2 n}} \frac{z^{2 n}}{(2 n)!} \\ = & 2 \sum_{n = 0}^{\infty} 2^{2 (p - q)} \frac{(\frac{a_{1}}{2})_{n} (\frac{a_{1} + 1}{2})_{n} (\frac{a_{2}}{2})_{n} (\frac{a_{2} + 1}{2})_{n} \dots (\frac{a_{p}}{2})_{n} (\frac{a_{p} + 1}{2})_{n}}{(\frac{b_{1}}{2})_{n} (\frac{b_{1} + 1}{2})_{n} (\frac{b_{2}}{2})_{n} (\frac{a_{b} + 1}{2})_{n} \dots (\frac{b_{q}}{2})_{n} (\frac{b_{q} + 1}{2})_{n}} \frac{z^{2 n}}{2^{2 n} (\frac{1}{2})_{n} n!} \\ = & 2_{2 p} F_{2 q + 1} (\frac{a_{1}}{2}, \frac{a_{1} + 1}{2}, \frac{a_{2}}{2}, \frac{a_{2} + 1}{2}, . . ., \frac{a_{p}}{2}, \frac{a_{p} + 1}{2}; \frac{b_{1}}{2}, \frac{b_{1} + 1}{2}, \frac{b_{2}}{2}, \frac{b_{2} + 1}{2}, . . ., \frac{b_{q}}{2}, \frac{b_{q} + 1}{2}, \frac{1}{2}; (2^{p - q - 1} z)^{2}) \end{array}$
[2]
$\begin{array}{rcl} _{p} F_{q} (a_{1}, a_{2}, . . ., a_{p}; b_{1}, b_{2}, . . ., b_{q}; z) -_{p} F_{q} (a_{1}, a_{2}, . . ., a_{p}; b_{1}, b_{2}, . . ., b_{q}; - z) & = & 2 \sum_{n = 0}^{\infty} \frac{(a_{1})_{2 n + 1} (a_{2})_{2 n + 1} \dots (a_{p})_{2 n + 1}}{(b_{1})_{2 n + 1} (b_{2})_{2 n + 1} \dots (b_{q})_{2 n + 1}} \frac{z^{2 n + 1}}{(2 n + 1)!} \\ = & 2 z \sum_{n = 0}^{\infty} \frac{(a_{1})_{2 n + 1} (a_{2})_{2 n + 1} \dots (a_{p})_{2 n + 1}}{(b_{1})_{2 n + 1} (b_{2})_{2 n + 1} \dots (b_{q})_{2 n + 1}} \frac{z^{2 n}}{2^{2 n} (\frac{3}{2})_{n} n!} \\ = & 2 z \sum_{n = 0}^{\infty} 2^{2 (p - q) n} \frac{a_{1} a_{2} \dots a_{p} (\frac{a_{1} + 1}{2})_{n} (\frac{a_{1}}{2} + 1)_{n} (\frac{a_{2} + 1}{2})_{n} (\frac{a_{2}}{2} + 1)_{n} \dots (\frac{a_{p} + 1}{2})_{n} (\frac{a_{p}}{2} + 1)_{n}}{b_{1} b_{2} \dots b_{q} (\frac{b_{1} + 1}{2})_{n} (\frac{b_{1}}{2} + 1)_{n} (\frac{b_{2} + 1}{2})_{n} (\frac{b_{2}}{2} + 1)_{n} \dots (\frac{b_{q} + 1}{2})_{n} (\frac{b_{q}}{2} + 1)_{n} (\frac{3}{2})_{n}} \frac{1}{n!} (\frac{z}{2})^{2 n} \\ = & 2 \frac{a_{1} a_{2} \dots a_{p}}{b_{1} b_{2} \dots b_{q}} z \sum_{n = 0}^{\infty} \frac{(\frac{a_{1} + 1}{2})_{n} (\frac{a_{1}}{2} + 1)_{n} (\frac{a_{2} + 1}{2})_{n} (\frac{a_{2}}{2} + 1)_{n} \dots (\frac{a_{p} + 1}{2})_{n} (\frac{a_{p}}{2} + 1)_{n}}{(\frac{b_{1} + 1}{2})_{n} (\frac{b_{1}}{2} + 1)_{n} (\frac{b_{2} + 1}{2})_{n} (\frac{b_{2}}{2} + 1)_{n} \dots (\frac{b_{q} + 1}{2})_{n} (\frac{b_{q}}{2} + 1)_{n} (\frac{3}{2})_{n}} \frac{1}{n!} (2^{p - q - 1} z)^{2 n} \\ = & 2 \frac{a_{1} a_{2} \dots a_{p}}{b_{1} b_{2} \dots b_{q}} z_{2 p} F_{2 q + 1} (\frac{a_{1} + 1}{2}, \frac{a_{1} + 2}{2}, \frac{a_{2} + 1}{2}, \frac{a_{2} + 2}{2}, . . ., \frac{a_{p} + 1}{2}, \frac{a_{p} + 2}{2}; \frac{b_{1} + 1}{2}, \frac{b_{1} + 2}{2}, \frac{b_{2} + 1}{2}, \frac{b_{2} + 2}{2}, . . ., \frac{b_{q} + 1}{2}, \frac{b_{q} + 2}{2}, \frac{3}{2}; (2^{p - q - 1} z)^{2}) \end{array}$

楕一種円積分

$\forall k \in [0, 1] : K (k) : = \int_{0}^{\frac{π}{2}} \frac{d θ}{\sqrt{1 - k^{2} \sin^{2} θ}}$

$K (k) = \frac{π}{2}_{2} F_{1} (\frac{1}{2}, \frac{1}{2}; 1; k^{2})$

[1] $f (x) = \frac{1}{\sqrt{1 - x}}$ とおくと $f^{(n)} (x) = \frac{(\frac{1}{2})_{n}}{(1 - x)^{\frac{2 n + 1}{2}}}$ なので
$f (x) = \sum_{n = 0}^{\infty} \frac{(\frac{1}{2})_{n}}{n!} x^{n}$
[2]ゆえにこれを用いると
$\begin{array}{rcl} K (k) & = & \int_{0}^{\frac{π}{2}} \sum_{n = 0}^{\infty} \frac{(\frac{1}{2})_{n}}{n!} k^{2 n} \sin^{2 n} θ d θ \\ = & \sum_{n = 0}^{\infty} \frac{(\frac{1}{2})_{n}}{n!} k^{2 n} \int_{0}^{\frac{π}{2}} \sin^{2 n} θ d θ \\ = & \sum_{n = 0}^{\infty} \frac{(\frac{1}{2})_{n}}{n!} k^{2 n} \frac{(\frac{1}{2})_{n}}{n!} \frac{π}{2} \\ = & \frac{π}{2}_{2} F_{1} (\frac{1}{2}, \frac{1}{2}; 1; k^{2}) \end{array}$

$\begin{array}{r} {\begin{cases} K (k) + K (i k) = π_{4} F_{3} (\frac{1}{4}, \frac{1}{4}, \frac{3}{4}, \frac{3}{4}; \frac{1}{2}, 1, \frac{1}{2}; k^{4}) \\ K (k) - K (i k) = \frac{π}{4} k^{2}_{4} F_{3} (\frac{3}{4}, \frac{3}{4}, \frac{5}{4}, \frac{5}{4}; 1, \frac{3}{2} \frac{3}{2}; k^{4}) \end{cases} \end{array}$

$K (\frac{1}{\sqrt{2}}) = \frac{Γ (\frac{1}{4})^{2}}{4 \sqrt{π}}$

$\begin{array}{rcl} K (\frac{1}{\sqrt{2}}) & = & \int_{0}^{\frac{π}{2}} \frac{d θ}{\sqrt{1 - \frac{1}{2} \sin^{2} θ}} \\ = & \sqrt{2} \int_{0}^{\frac{π}{2}} \frac{d θ}{\sqrt{2 - \sin^{2} θ}} (\sin θ = x) \\ = & \sqrt{2} \int_{0}^{1} \frac{d x}{\sqrt{(1 - x^{2}) (2 - x^{2})}} (x^{2} = y) \\ = & \frac{1}{\sqrt{2}} \int_{0}^{1} \frac{d y}{\sqrt{y (1 - y) (2 - y)}} (1 - y = z) \\ = & \frac{1}{\sqrt{2}} \int_{0}^{1} \frac{d z}{\sqrt{z (1 - z) (1 + z)}} \\ = & \frac{1}{\sqrt{2}} \int_{0}^{1} \frac{d z}{\sqrt{z (1 - z^{2})}} \\ = & \frac{1}{2 \sqrt{2}} \int_{0}^{1} \frac{d w}{w^{\frac{3}{4}} (1 - w)^{\frac{1}{2}}} \\ = & \frac{1}{2 \sqrt{2}} B (\frac{1}{4}, \frac{1}{2}) \\ = & \frac{Γ (\frac{1}{4}) Γ (\frac{1}{2})}{2 \sqrt{2} Γ (\frac{3}{4})} \\ = & \frac{Γ (\frac{1}{4})^{2} \sqrt{π}}{2 \sqrt{2} Γ (\frac{1}{4}) Γ (1 - \frac{1}{4})} \\ = & \frac{Γ (\frac{1}{4})^{2}}{4 \sqrt{π}} \end{array}$

$K (i \frac{1}{\sqrt{2}}) = \frac{π}{\sqrt{6}}_{2} F_{1} (\frac{1}{2}, \frac{1}{2}; 1; \frac{1}{3})$

$\begin{array}{rcl} K (i \frac{1}{\sqrt{2}}) & = & \int_{0}^{\frac{π}{2}} \frac{d θ}{\sqrt{1 + \frac{1}{2} \sin^{2} θ}} \\ = & \sqrt{2} \int_{0}^{\frac{π}{2}} \frac{d θ}{\sqrt{2 + \sin^{2} θ}} (\sin θ = x) \\ = & \sqrt{2} \int_{0}^{1} \frac{d x}{\sqrt{(1 - x^{2}) (2 + x^{2})}} (x^{2} = y) \\ = & \frac{1}{\sqrt{2}} \int_{0}^{1} \frac{d y}{\sqrt{y (1 - y) (2 + y)}} (y = 1 - z) \\ = & \frac{1}{\sqrt{2}} \int_{0}^{1} \frac{d z}{\sqrt{z (1 - z) (3 - z)}} \\ = & \frac{1}{\sqrt{6}} \int_{0}^{1} z^{\frac{1}{2} - 1} (1 - z)^{\frac{1}{2} - 1} (1 - \frac{1}{3} z)^{- \frac{1}{2}} d z \\ = & \frac{1}{\sqrt{6}} \frac{Γ (\frac{1}{2}) Γ (\frac{1}{2})}{Γ (1)}_{2} F_{1} (\frac{1}{2}, \frac{1}{2}; 1; \frac{1}{3}) \\ = & \frac{π}{\sqrt{6}}_{2} F_{1} (\frac{1}{2}, \frac{1}{2}; 1; \frac{1}{3}) \end{array}$

$\begin{array}{r} {\begin{cases} _{4} F_{3} (\frac{1}{4}, \frac{1}{4}, \frac{3}{4}, \frac{3}{4}; \frac{1}{2}, 1, \frac{1}{2}; \frac{1}{4}) = \frac{Γ (\frac{1}{4})^{2}}{4 π \sqrt{π}} + \frac{1}{\sqrt{6}}_{2} F_{1} (\frac{1}{2}, \frac{1}{2}; 1; \frac{1}{3}) \\ _{4} F_{3} (\frac{3}{4}, \frac{3}{4}, \frac{5}{4}, \frac{5}{4}; 1, \frac{3}{2}, \frac{3}{2}; \frac{1}{4}) = \frac{2 Γ (\frac{1}{4})^{2}}{π \sqrt{π}} - 4 \sqrt{\frac{2}{3}}_{2} F_{1} (\frac{1}{2}, \frac{1}{2}; 1; \frac{1}{3}) \end{cases} \end{array}$

$- \log (1 - x) = x_{2} F_{1} (1, 1; 2; x)$

[1]
$\begin{array}{rcl} \frac{d^{n}}{d x^{n}} \log (1 - x) & = & - \frac{(n - 1)!}{(1 - x)^{n}} \end{array}$
[2]
$\begin{array}{rcl} - \log (1 - x) & = & \sum_{n = 1}^{\infty} \frac{1}{n} x^{n} \\ = & \sum_{n = 1}^{\infty} \frac{(n - 1)! (n - 1)!}{n!} \frac{x^{n}}{(n - 1)!} \\ = & x \sum_{n = 0}^{\infty} \frac{n! n!}{(n + 1)!} \frac{x^{n}}{n!} \\ = & x_{2} F_{1} (1, 1; 2; x) \end{array}$

$ψ (α, β, γ, z) = \int_{0}^{1} x^{α - 1} (1 - x)^{β - 1} (1 - z x)^{- γ} d x$ とすると以下の様に書ける。
$ψ (α, β, γ, z) = \frac{Γ (α) Γ (β)}{Γ (α + β)}_{2} F_{1} (α, γ; α + β; z)$

$\begin{array}{rcl} ψ (α, β, γ, z) & = & \int_{0}^{1} x^{α - 1} (1 - x)^{β - 1} (1 - z x)^{- γ} d x \\ = & \sum_{n = 0}^{\infty} \frac{(γ)_{n}}{n!} z^{n} \int_{0}^{1} x^{α + n - 1} (1 - x)^{β - 1} d x \\ = & \sum_{n = 0}^{\infty} \frac{(γ)_{n}}{n!} z^{n} \frac{Γ (α + n) Γ (β)}{Γ (α + β + n)} \\ = & \frac{Γ (α) Γ (β)}{Γ (α + β)} \sum_{n = 0}^{\infty} \frac{(α)_{n} (γ)_{n}}{(α + β)_{n}} \frac{z^{n}}{n!} \\ = & \frac{Γ (α) Γ (β)}{Γ (α + β)}_{2} F_{1} (α, γ; α + β; z) \end{array}$

$\forall n \in N_{0} : \forall N \in N : (\frac{1}{N})_{n} (\frac{2}{N})_{n} \dots (\frac{N - 1}{N})_{n} = \frac{(n N)!}{n! N^{n N}}$

$\begin{array}{rcl} (\frac{1}{N})_{n} (\frac{2}{N})_{n} \dots (\frac{N - 1}{N})_{n} & = & \frac{1}{N} \frac{2}{N} \dots \frac{N - 1}{N} \frac{N + 1}{N} \frac{N + 2}{N} \dots \frac{2 N - 1}{N} \dots \frac{(n - 1) N + 1}{N} \frac{(n - 1) N + 2}{N} \dots \frac{n N - 1}{N} \\ = & \frac{(n N)!}{n! N^{n N}} \end{array}$

$\begin{array}{r} \forall N \in N : \exists Q, R \in N_{0} (0 < R < N) s . t . (\frac{Q N + R}{N})_{n} (\frac{Q N + R + 1}{N})_{n} \dots (\frac{Q N + N - 1}{N})_{n} (\frac{(Q + 1) N + 1}{N})_{n} \dots (\frac{(Q + 1) N + R - 1}{N})_{n} = \frac{Q! {(Q + n) N + R - 1}!}{(Q + n)! (Q N + R - 1)! N^{n N}} \end{array}$

[1] $R = 1$ とした場合。
$\begin{array}{rcl} (\frac{Q N + 1}{N})_{n} (\frac{Q N + 2}{N})_{n} \dots (\frac{Q N + N - 1}{N})_{n} & = & \frac{Q N + 1}{N} \frac{Q N + 2}{N} \dots \frac{Q N + N - 1}{N} \frac{Q N + N + 1}{N} \frac{Q N + N + 2}{N} \dots \frac{Q N + N + N - 1}{N} \dots \frac{(Q + n - 1) N + 1}{N} \frac{(Q + n - 1) N + 2}{N} \dots \frac{(n + Q) N - 1}{N} \\ = & \frac{Q! {(Q + n) N}!}{(Q + n)! (Q N)! N^{n N}} \end{array}$
[2] $R \neq 1$ とした場合。
$\begin{array}{rcl} (\frac{Q N + R}{N})_{n} (\frac{Q N + R + 1}{N})_{n} \dots (\frac{Q N + N - 1}{N})_{n} (\frac{(Q + 1) N + 1}{N})_{n} \dots (\frac{(Q + 1) N + R - 1}{N})_{n} & = & \frac{Q N + R}{N} \frac{Q N + R + 1}{N} \dots \frac{Q N + N - 1}{N} \frac{(Q + 1) N + 1}{N} \frac{(Q + 1) N + 2}{N} \dots \frac{(Q + 1) N + R - 1}{N} \frac{(Q + 1) N + R}{N} \frac{(Q + 1) N + R + 1}{N} \dots \frac{(Q + 1) N + N - 1}{N} \frac{(Q + 2) N + 1}{N} \dots \frac{(Q + 2) N + R - 1}{N} \frac{(Q + n - 1) N + R}{N} \frac{(Q + n - 1) N + R + 1}{N} \dots \frac{(Q + n - 1) N + N - 1}{N} \frac{(Q + n) N + 1}{N} \dots \frac{(Q + n) N + R - 1}{N} \\ = & \frac{Q! {(Q + n) N + R - 1}!}{(Q + n)! (Q N + R - 1)! N^{n N}} \end{array}$

例

$(\frac{1}{2})_{n} = \frac{(2 n)!}{n! 2^{2 n}}$
$(\frac{3}{2})_{n} = \frac{{2 (n + 1)}!}{(n + 1)! n 2^{2 n}}$
$(\frac{1}{4})_{n} (\frac{2}{4})_{n} (\frac{3}{4})_{n} = \frac{(4 n)!}{n! 4^{4 n}}$
$(\frac{2}{4})_{n} (\frac{3}{4})_{n} (\frac{5}{4})_{n} = \frac{(4 n + 1)!}{n! 4^{4 n}}$

上記の式を用いると

\begin{array}{rcl} \frac{(\frac{1}{4})_{n} (\frac{1}{4})_{n} (\frac{3}{4})_{n} (\frac{3}{4})_{n}}{(\frac{1}{2})_{n} (\frac{1}{2})_{n}} & = & \frac{{(4 n)!}^{2}}{(n!)^{2} 4^{8 n}} \frac{(n!)^{4} 2^{8 n}}{{(2 n)!}^{4}} \\ = & \frac{{(4 n)!}^{2} (n!)^{2}}{4^{4 n} {(2 n)!}^{4}} \\ = & \frac{{(4 n)!}^{2} (n!)^{2}}{4^{4 n} {(2 n)!}^{4}} \\ = & \frac{{(4 n)!}^{2} (n!)^{2}}{{(2 n)!}^{4}} \frac{1}{256^{n}} \end{array}

ゆえに、

\begin{array}{rcl} _{4} F_{3} (\frac{1}{4}, \frac{1}{4}, \frac{3}{4}, \frac{3}{4}; \frac{1}{2}, 1, \frac{1}{2}; \frac{1}{4}) & = & \sum_{n = 0}^{\infty} \frac{{(4 n)!}^{2}}{{(2 n)!}^{4}} \frac{1}{1024^{n}} \\ = & \frac{Γ (\frac{1}{4})^{2}}{4 π \sqrt{π}} + \frac{1}{\sqrt{6}} \sum_{n = 0}^{\infty} \frac{{(2 n)!}^{2}}{2^{4 n} (n!)^{3}} \frac{1}{3^{n}} \\ = & \frac{Γ (\frac{1}{4})^{2}}{4 π \sqrt{π}} + \frac{1}{\sqrt{6}} \sum_{n = 0}^{\infty} \frac{{(2 n)!}^{2}}{(n!)^{3}} \frac{1}{48^{n}} \end{array}

同様に

\begin{array}{rcl} \frac{(\frac{3}{4})_{n} (\frac{3}{4})_{n} (\frac{5}{4})_{n} (\frac{5}{4})_{n}}{(\frac{3}{2})_{n} (\frac{3}{2})_{n}} & = & \frac{{(4 n + 1)!}^{2}}{(n!)^{2} 4^{8 n}} \frac{(n!)^{2} 2^{4 n}}{{(2 n)!}^{2}} \frac{{(n + 1)!}^{2} n 2^{4 n}}{[{2 (n + 1)}!]^{2}} \\ = & \frac{(4 n + 1)^{2} {(4 n)!}^{2} (n!)^{2} n}{4^{4 n + 1} (2 n + 1)^{2} {(2 n)!}^{4}} \end{array}

\begin{array}{rcl} _{4} F_{3} (\frac{3}{4}, \frac{3}{4}, \frac{5}{4}, \frac{5}{4}; 1, \frac{3}{2}, \frac{3}{2}; \frac{1}{4}) & = & \frac{1}{4} \sum_{n = 0}^{\infty} \frac{(4 n + 1)^{2} {(4 n)!}^{2} n}{(2 n + 1)^{2} {(2 n)!}^{4}} \frac{1}{1024^{n}} \\ = & \frac{2 Γ (\frac{1}{4})^{2}}{π \sqrt{π}} - 4 \sqrt{\frac{2}{3}} \sum_{n = 0}^{\infty} \frac{{(2 n)!}^{2}}{(n!)^{3}} \frac{1}{48^{n}} \end{array}

応用2

Watsonの補題

積分可能な関数 $f : R_{+} \to C$ が次の性質を満たすとする。
(1) $\exists a > 0 s . t . | f (t) | = O (e^{a t})$
(2) $f (t) ≃ \sum_{m = 0}^{\infty} c_{m} t^{a_{m}}$ ただし、 ${a_{m}}_{m \in N_{0}}$ は単調増加な数列
この時、次の積分： $I_{n} = \int_{0}^{\infty} e^{- n t} f (t) d t$ を定めると、次の様に書ける。
$I_{n} ≃ \sum_{m = 0}^{\infty} c_{m} \frac{Γ (a_{m} + 1)}{n^{a_{m} + 1}}$

(1)の条件により、 $| a | < n$ の様にとる。すると
$\exists C \in R_{+} s . t . | f (t) | \leq C e^{a t} < C e^{n t}$
ゆえに
$\begin{array}{rcl} | \int_{0}^{\infty} f (x) e^{- n x} d x | & \leq & \int_{0}^{\infty} | f (x) | e^{- n x} d x \\ < & C \int_{0}^{\infty} e^{a x} e^{- n x} d x \\ = & C \int_{0}^{\infty} e^{- (n - a) x} d x \\ = & \frac{C}{n - a} < + \infty \end{array}$
絶対収束する。
次にその様な自然数 $n$ を取ります。
$\begin{array}{rcl} I_{n} & = & \int_{0}^{\infty} f (x) e^{- n x} d x \\ ≃ & \int_{0}^{\infty} \sum_{m = 0}^{\infty} c_{m} x^{a_{m}} e^{- n x} d x (n x = y) \\ = & \sum_{m = 0}^{\infty} \frac{c_{m}}{n^{a_{m + 1}}} \int_{0}^{\infty} x^{a_{m + 1 - 1}} e^{- x} d x \\ = & \sum_{m = 0}^{\infty} c_{m} \frac{Γ (a_{m} + 1)}{n^{a_{m + 1}}} \end{array}$

Abelの総和公式1

数列 ${a_{n}}_{n \in N}, {b_{n}}_{n \in N}$ に対して次の様な式が成り立つ。
$\begin{array}{r} {\begin{cases} A_{n} : = \sum_{m = 1}^{n} a_{m} \\ \sum_{n = 1}^{N} a_{n} b_{n} = A_{N} b_{N} + \sum_{n = 1}^{N - 1} A_{n} (b_{n} - b_{n + 1}) \end{cases} \end{array}$

下の図を参照すればよい。

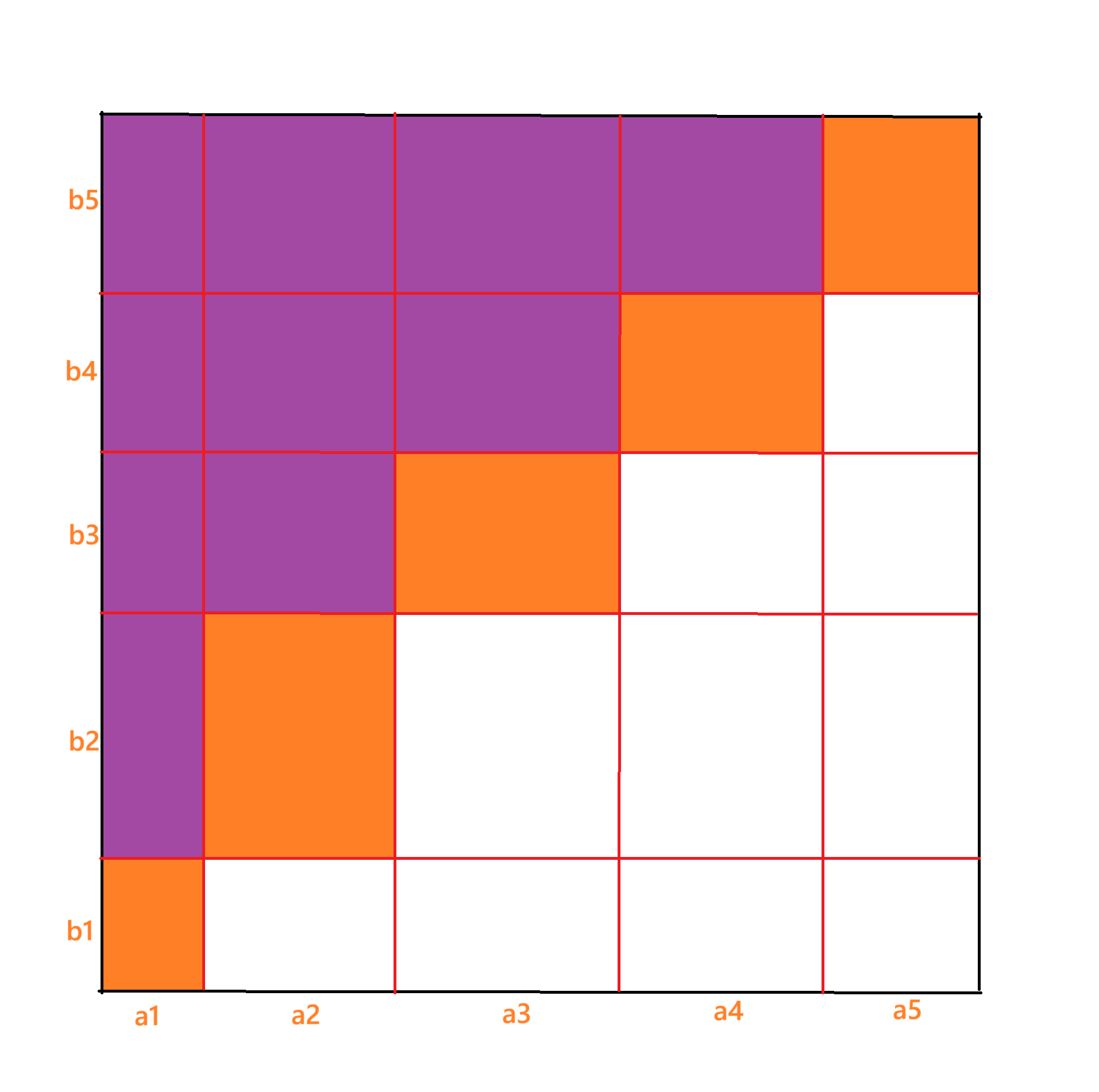Abelの総和法

Abelの総和公式2

数列 ${a_{n}}_{n \in N}$ と微分可能な関数 $f \in C^{1} (0, x)$ に対して以下の式が成り立つ。
$\begin{array}{r} {\begin{cases} A (x) : = \sum_{0 \leq n \leq ⌊ x ⌋} a_{n} \\ \sum_{0 \leq n \leq x} a_{n} f (n) = A (⌊ x ⌋) f (⌊ x ⌋) - \int_{0}^{⌊ x ⌋} A (y) f^{^{'}} (y) d y \end{cases} \end{array}$

[1]右辺の積分について少し考察すれば分かる。
$\begin{array}{rcl} \int_{0}^{⌊ x ⌋} A (y) f^{^{'}} (y) d y & = & \sum_{k = 1}^{⌊ x ⌋} \int_{k - 1}^{k} A (y) f^{^{'}} (y) d y \\ = & \sum_{k = 1}^{⌊ x ⌋} lim_{ϵ \to 0 + 0} \int_{k - 1}^{k - ϵ} A (y) f^{^{'}} (y) d y \\ = & \sum_{k = 1}^{⌊ x ⌋} A (k - 1) lim_{ϵ \to 0 + 0} \int_{k - 1}^{k - ϵ} f^{^{'}} (y) d y \\ = & \sum_{k = 1}^{⌊ x ⌋} A (k - 1) lim_{ϵ \to 0 + 0} {f (k - ϵ) - f (k - 1)} \\ = & \sum_{k = 1}^{⌊ x ⌋} A (k - 1) {f (k) - f (k - 1)} \end{array}$
[2] $f (k) = b_{k}$ とおくと、Abelの総和と一致する事が分かるので証明終了。

積分可能な関数 $f : R_{+} \to C$ が次の性質を満たすとする。
$\exists a > 0 s . t . | f (t) | = O (e^{a t})$
すると次の様な積分変換を定義することが出来る。
$\forall a < R e (s) : L [f] (s) = \int_{0}^{\infty} f (x) e^{- s x} d x$
すると次の積分変換により元に戻る。
$L^{- 1} [F] (x) = \frac{1}{2 π i} \int_{c - i \infty}^{c + i \infty} F (s) e^{s x} d s$

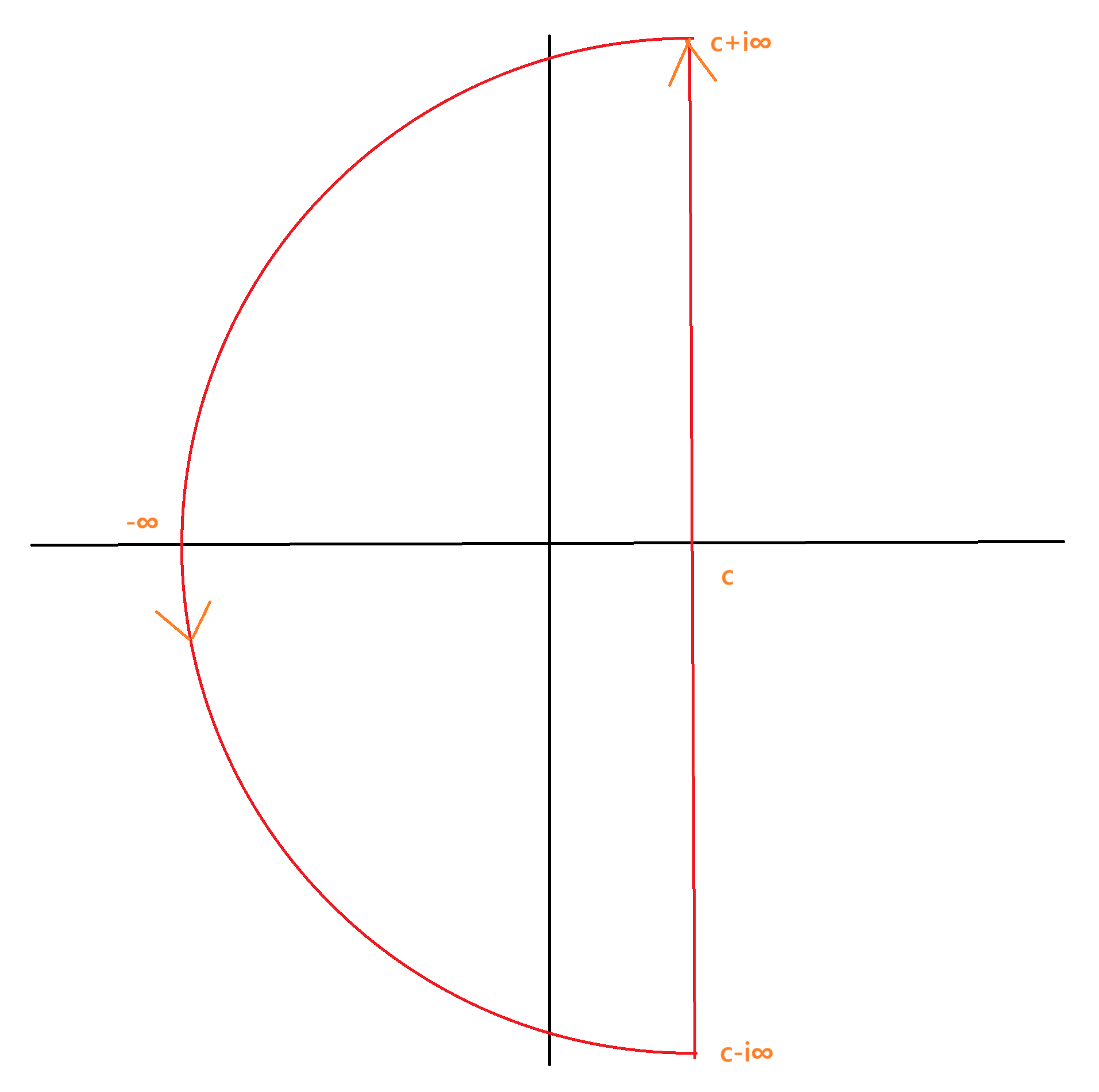逆Laplace変換

解析的表示 $f (z) = \sum_{n = 0}^{\infty} a_{n} z^{n}$ が存在する場合のみ示す。
[1]仮定より、Laplace変換は常に定義出来なおかつ、それは絶対収束しますので次の様な計算が出来る。
$\begin{array}{rcl} L [f] (s) & = & \int_{0}^{\infty} f (z) e^{- s z} d z \\ = & \int_{0}^{\infty} \sum_{n = 0}^{\infty} a_{n} z^{n} e^{- s z} d z \\ = & \sum_{n = 0}^{\infty} a_{n} \int_{0}^{\infty} z^{n} e^{- s z} d z \\ = & \sum_{n = 0}^{\infty} \frac{a_{n} n!}{s^{n + 1}} \end{array}$
[2]この得られた級数について以下の計算を行います。
$\begin{array}{rcl} L^{- 1} [f] (z) & = & \frac{1}{2 π i} \int_{c - i \infty}^{c + i \infty} \sum_{n = 0}^{\infty} \frac{a_{n} n!}{s^{n + 1}} e^{s z} d s + \int_{Γ} \sum_{n = 0}^{\infty} \frac{a_{n} n!}{s^{n + 1}} e^{s z} d s \\ = & \sum_{n = 0}^{\infty} \frac{1}{2 π i} \int_{c - i \infty}^{c + i \infty} \frac{a_{n} n!}{s^{n + 1}} \sum_{m = 0}^{\infty} \frac{s^{m} z^{m}}{m!} d s \\ = & \sum_{m = 0}^{\infty} \sum_{n = 0}^{\infty} \frac{a_{n} n! z^{m}}{m!} \frac{1}{2 π i} \int_{c - i \infty}^{c + i \infty} \frac{1}{s^{n - m + 1}} d s \\ = & \sum_{m = 0}^{\infty} \sum_{n = 0}^{\infty} \frac{a_{n} n! z^{m}}{m!} δ_{n, m} \\ = & \sum_{n = 0}^{\infty} a_{n} z^{n} \\ = & f (z) \end{array}$

Perronの公式

数列 ${a_{n}}_{n \in N_{0}}$ により定まる二つの級数を考える。
$\begin{array}{r} {\begin{cases} f (s) : = \sum_{n = 1}^{\infty} \frac{a_{n}}{n^{s}} \\ A (x) : = \sum_{1 \leq n \leq ⌊ x ⌋} a_{n} \end{cases} \end{array}$
すると以下の式が成り立つ。
$A (\log x) = \frac{1}{2 π i} \int_{c - i \infty}^{c + i \infty} f (s) \frac{x^{s}}{s} d s$

[1]Abelの総和法により、任意の微分可能な関数 $φ \in C^{1} (1, x)$ に対して以下の式が成り立つ。
$\begin{array}{r} {\begin{cases} A (x) = \sum_{1 \leq n \leq ⌊ x ⌋} a_{n} \\ \sum_{1 \leq n \leq ⌊ x ⌋} a_{n} φ (n) = A (⌊ x ⌋) φ (⌊ x ⌋) - \int_{1}^{⌊ x ⌋} A (t) φ^{^{'}} (t) d t \end{cases} \end{array}$
[2] $φ (x) : = x^{- s}$ とおく。すると下記の様に書き直せる。
$\begin{array}{r} \sum_{1 \leq n \leq ⌊ x ⌋} \frac{a_{n}}{n^{s}} = \frac{A (⌊ x ⌋)}{⌊ x ⌋^{s}} + s \int_{1}^{⌊ x ⌋} \frac{A (t)}{t^{s + 1}} d t \end{array}$
[3] $x \to \infty$ とする。すると以下の式が成り立つ。
$\begin{array}{rcl} f (s) & = & s \int_{1}^{\infty} \frac{A (t)}{t^{s + 1}} d t (t = e^{τ}) \\ = & s \int_{0}^{\infty} A (τ) e^{- s τ} d τ \end{array}$
[4]ゆえに
$\frac{f (s)}{s} = \int_{0}^{\infty} A (τ) e^{- s τ} d τ \equiv L [A (τ)] (s)$
[5][4]の右辺はLaplace変換なのでLaplace変換の逆変換を行う事で
$A (x) = \frac{1}{2 π i} \int_{c - i \infty}^{c + i \infty} \frac{f (s)}{s} e^{s x} d s$
最後に $x = \log y$ の様に置き換えて
$A (\log y) = \frac{1}{2 π i} \int_{c - i \infty}^{c + i \infty} \frac{f (s)}{s} y^{s} d s$

応用1では適当に数列を選んで三次の加速度を持つ零数列を構成出来ましたが...
しかし、 $\sum_{n = 0}^{\infty} w_{n} a_{n}$ の値が不明であり実用に足らなかったです。
ですが、今なら超幾何関数に関する公式を幾つか考え、特に楕円積分の特殊値を求めました。これらの値は既に分かっているものですから、この様な数列の一次結合を用いて級数の加速を行う事が出来るかもしれません。
僕はその様な期待を胸に計算を進めてきたのですがここで残念なお知らせ。
少なくとも、今回求めた楕円関数の特殊値、 $l o g 2$ , $\sqrt{2}$ の一次結合により構成した $w_{n}$ では $3$ 次の加速度を持つ零数列を構成出来ないようです。
ただ、構成できない事を証明するのも案外有益なのではないかと思い一つ例をの載せます。
良かったらこの例にチャレンジしてみてください。

$f (x) = \frac{1}{(x + 1)^{2}}$ とおくと、 $\forall n \in N_{0} : f^{(n)} (x) = \frac{(- 1)^{n} (n + 1)!}{(x + 1)^{n + 2}}$ とするとEuler-Maclaurin展開により
$\sum_{n = 0}^{N - 1} \frac{1}{(n + 1)^{2}} = \frac{π^{2}}{6} - \frac{1}{N} + \frac{1}{2 N^{2}} + O (\frac{1}{N^{3}})$
と書けます。この事を用いて3次の加速度を持つ零数列 ${w_{n}}_{n \in N_{0}}$ を作りたいとします。
しかし、下記の数列の $C$ 係数の一次結合をどのようにとっても3次の加速度を持つ零数列を構成できない事を証明してください。
$\begin{array}{r} {\begin{cases} f_{n 0} = \frac{{{2 (n + 1)}!}^{2} (n + 1)^{2}}{{(n + 1)!}^{3} 32^{n + 1}} \\ f_{n 1} = (- 1)^{n} (n + 1) \\ f_{n 2} = \frac{(\begin{array}{c} 2 (n + 1) \\ n + 1 \end{array}) (n + 1)^{2}}{2^{2 (n + 1)} (n + 1)!} \frac{1}{2^{n + 1}} \end{cases} \end{array}$

[1]まず以下の様に適当な係数 $A, B, C$ を用いて下記の様な数列を作成する。
$w_{n} = A \frac{{{2 (n + 1)}!}^{2} (n + 1)^{2}}{{(n + 1)!}^{3} 32^{n + 1}} + B (- 1)^{n} (n + 1) + C \frac{(\begin{matrix} 2 (n + 1) \\ n + 1 \end{matrix}) (n + 1)^{2}}{2^{2 (n + 1)} (n + 1)!} \frac{1}{2^{n + 1}}$
[2]以下の式が成り立つ様 $A, B, C$ を定める。
$\begin{array}{r} {\begin{cases} \sum_{n = 0}^{N - 1} \frac{w_{n}}{(n + 1)^{2}} = δ - \frac{1}{N} + \frac{1}{2 N^{2}} + O (\frac{1}{N^{3}}) \\ \sum_{n = 0}^{\infty} \frac{w_{n}}{(n + 1)^{2}} = A \frac{Γ (\frac{1}{4})^{2}}{2 π \sqrt{π}} + B \log 2 + C \sqrt{2} \end{cases} \end{array}$
漸近表示を求める。
[3]
$\begin{array}{rcl} \frac{{(2 n)!}^{2}}{(n!)^{3} 32^{n}} & = & \frac{2 π (2 n)^{2 n + 1}}{e^{4 n}} \frac{e^{3 n}}{2 π \sqrt{2 π} n^{3 n + \frac{3}{2}} 32^{n}} \\ = & \frac{1}{e} \sqrt{\frac{2}{π}} \frac{2^{2 n}}{n^{n + \frac{1}{2}} 32^{n}} \\ = & \frac{1}{e} \sqrt{\frac{2}{π}} \frac{1}{n^{n + \frac{1}{2}} 8^{n}} \end{array}$
$\begin{array}{rcl} \frac{(\begin{array}{c} 2 n \\ n \end{array})}{2^{3 n} n!} & = & \frac{4^{n}}{2^{3 n} \sqrt{π n}} \frac{e^{n}}{\sqrt{2 π} n^{n + \frac{1}{2}}} \\ = & \frac{1}{π \sqrt{2}} \frac{e^{n}}{n^{n + 1} 2^{n}} \end{array}$
$\begin{array}{rcl} \sum_{n = 1}^{N} \frac{w_{n - 1}}{n^{2}} & ≃ & A \frac{1}{e} \sqrt{\frac{2}{π}} \sum_{n = 1}^{N} \frac{1}{n^{n + \frac{1}{2}} 8^{n}} + B \sum_{n = 1}^{N} \frac{(- 1)^{n - 1}}{n} + C \frac{1}{π \sqrt{2}} \sum_{n = 1}^{N} \frac{e^{n}}{n^{n + 1} 2^{n}} \end{array}$
[4]そこで以下の様な記号を定める。
$\begin{array}{r} {\begin{cases} f (p, q; x) : = \frac{1}{x^{x + p} q^{x}} \\ ψ (x) : = x (\log x + \log q) + p \log x \\ S (p, q; f) (N) : = \sum_{n = 1}^{N} f (p, q; n) \\ F (p, q; s) = \sum_{n = 1}^{\infty} \frac{f (p, q; n)}{n^{s}} \end{cases} \end{array}$
[5]Perronの公式を用いる。
$\begin{array}{rcl} S (p, q; f) (⌊ \log N ⌋) & = & \frac{1}{2 π i} \int_{c - i \infty}^{c + i \infty} F (p, q; s) \frac{N^{s}}{s} d s \end{array}$
$s = 0$ の留数について
$\frac{F (p, q; s) N^{s}}{s} = \frac{1}{s} F (p, q; s) e^{s \log N}$
$\begin{array}{r} {\begin{cases} F (p, q; s) = F (p, q; 0) + s F^{^{'}} (p, q; 0) + O (s^{2}) \\ e^{s \log N} = 1 + s \log N + O (s^{2}) \end{cases} \end{array}$
$\begin{array}{rcl} \frac{F (p, q; s) N^{s}}{s} & = & \frac{1}{s} {F (p, q; 0) + s F^{^{'}} (p, q; 0) + O (s^{2})} {1 + s \log N + O (s^{2})} \\ = & \frac{F (p, q; 0)}{s} + F (p, q; 0) \log N + F^{^{'}} (p, q; 0) + O (s) \end{array}$
以上の計算により
$\begin{array}{rcl} R e s_{s = 0} \frac{F (p, q; s) N^{s}}{s} & = & F (0) \\ = & \sum_{n = 1}^{\infty} f (p, q; n) \end{array}$
すなわち
$\forall R \in R_{+} : S (p, q, f) (⌊ \log N ⌋) = \sum_{n = 1}^{\infty} \frac{1}{n^{n + p} q^{n}} + O (N^{R})$
[6]つまり、与えられた数列 $f_{n 0}, f_{n 1}, f_{n 2}$ の $C$ 係数の一次結合をどのようにとっても3次の加速度を持つ零数列を構成できない事が証明できました。