3
高校数学解説
a・b=a1b1+a2b2の証明
96
0
$$$$
$θ$を$\overrightarrow{a}$と$\overrightarrow{b}$のなす角とすると
$\overrightarrow{a}・\overrightarrow{b} = |a||b|cosθ$
$\overrightarrow{a}=(a_1,a_2)$、$\overrightarrow{b}=(b_1,b_2)$
⇒$\overrightarrow{a}・\overrightarrow{b} = a_1b_1+a_2b_2$
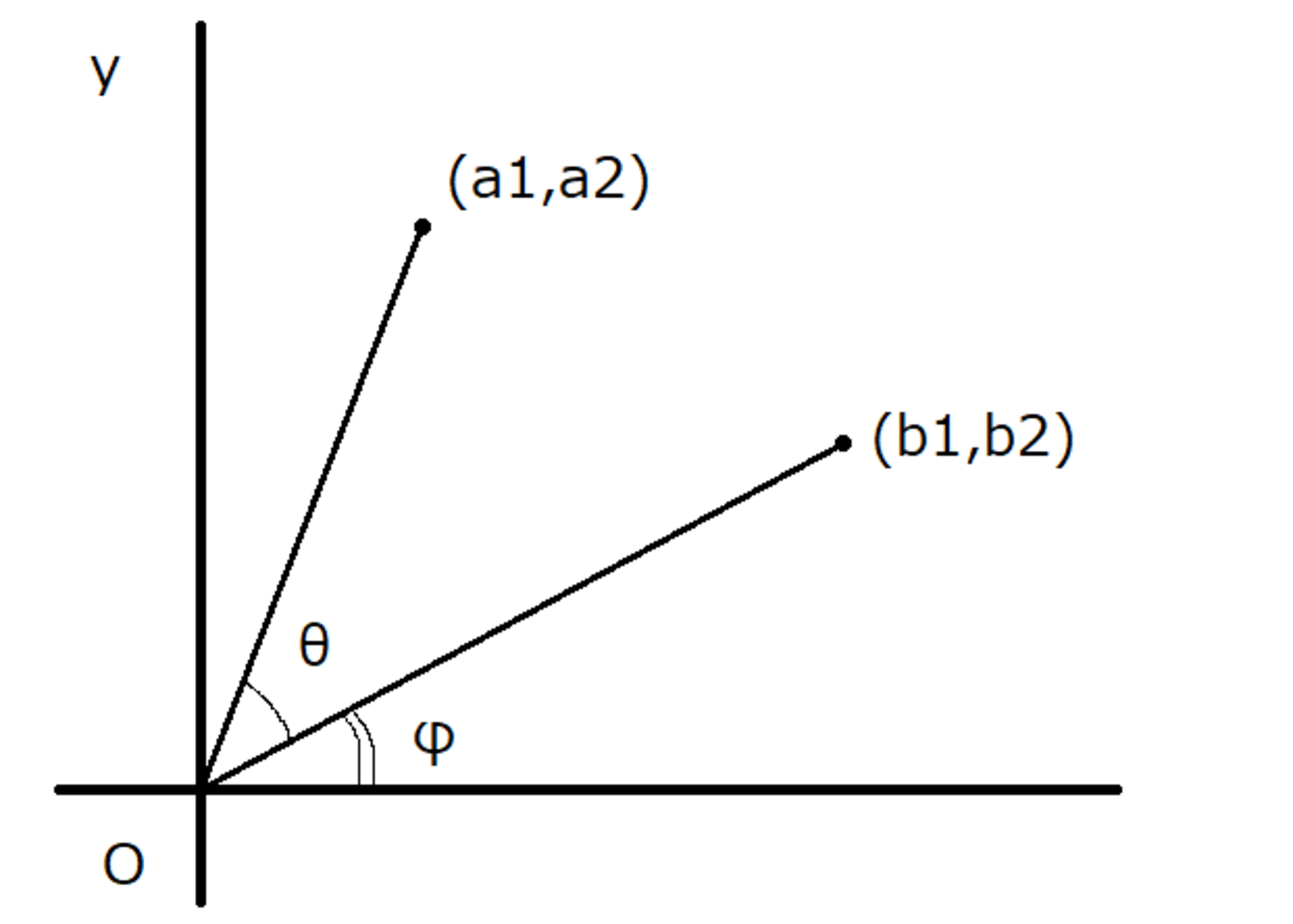a・b=a1b1+a2b2の証明
$$a_1b_1 + a_2b_2$$
$$=|a|cos(θ+φ)|b|cosφ + |a|sin(θ+φ)|b|sinφ$$
$$=|a||b| \lbrace cos(θ+φ)cosφ + sin(θ+φ)sinφ \rbrace$$
$$=|a||b|cos\lbrace (θ+φ) - φ \rbrace$$
$$=|a||b|cosθ$$
$$=a・b$$
投稿日：2021年10月20日
この記事を高評価した人
この記事を高評価した人
高評価したユーザはいません
この記事に送られたバッジ
この記事に送られたバッジ
バッジはありません。
投稿者
投稿者
コメント
コメント
他の人のコメント
コメントはありません。
読み込み中...
読み込み中