正五角形を並べてフィボナッチ数列を得る方法
はじめに
この記事では、Twitterで数学を愛する会さんが開催していた【フィボナッチ計算選手権】($n$番目のフィボナッチ数を計算する方法)に私が投稿した内容について解説したいと思います。
y=x/Φ
— ａｐｕ (@apu_yokai) October 31, 2021
のグラフ上を正の方向に点が移動するとき、x=整数の直線と、y=整数の直線と交差する順番に合わせて正五角形を上向きまたは下向きに図のように並べる。
並べた正五角形と接するように図のように五芒星を並べると、五芒星の足の間の正五角形の数としてフィボナッチ数が順番に現れる。⭐️ pic.twitter.com/wr2MuuYe4c
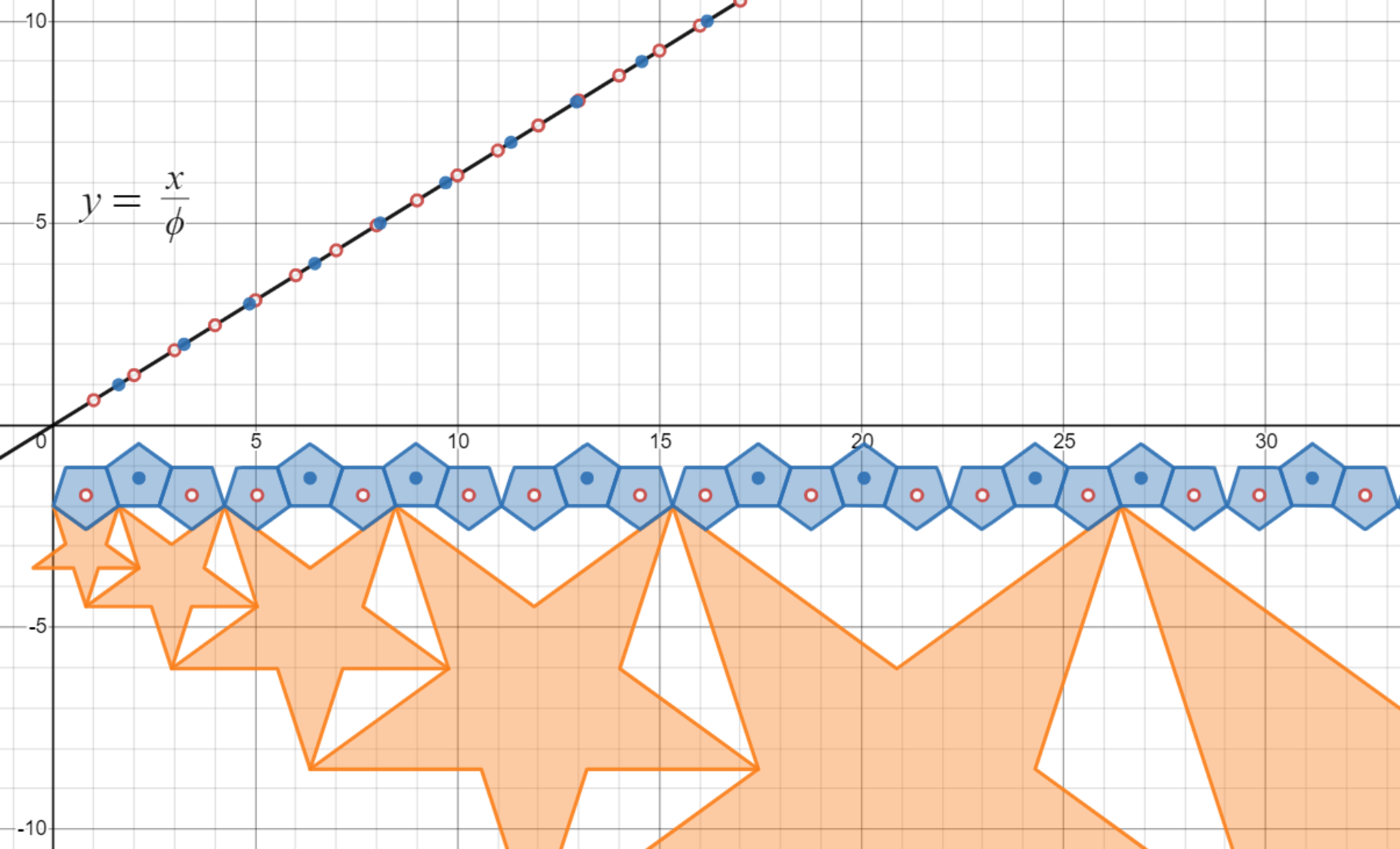五芒星の足の間の星の数は1,2,3,5,8,……となっている
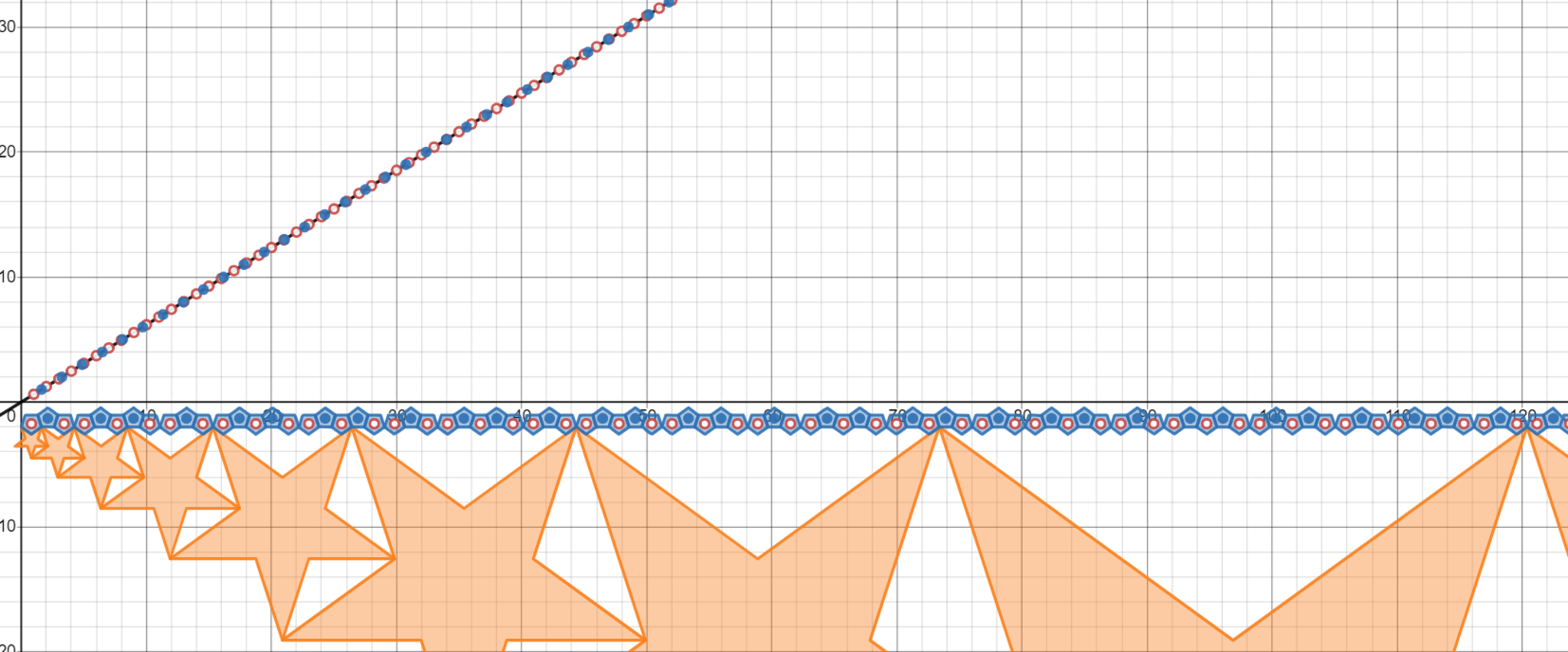どこまでいってもフィボナッチ数が順番に現れる
なお、$\varphi$ は黄金比(黄金数)を表す次の定数です。
$\varphi=\dfrac{1+\sqrt{5}}{2}$
また、$n$ 番目のフィボナッチ数を $F_n$ と表します。
フィボナッチ数の総和
突然ですが、フィボナッチ数の総和は次のように表すことができます。
${\displaystyle \sum_{k=1}^{n}F_n =F_{n+2}-1 }$
この式は後で使います。
なお、この式が成り立つことは、次のように考えればわかると思います。
$S(n):=1+1+2+3+5+8+\cdots+F_n$
$\begin{align} 1+S(n)&=\underbrace{1+1}+1+2+3+5+8+\cdots+F_n\\ &=\,\,\,\,\,\,\,\underbrace{2+1}+2+3+5+8+\cdots+F_n\\ &=\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underbrace{3+2}+3+5+8+13+\cdots+F_n\\ &=\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underbrace{5+3}+5+8+13+21+\cdots+F_n\\ &=\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underbrace{8+5}+8+13+21+34+\cdots+F_n\\ &\qquad \vdots\\ &=\underbrace{F_{n}+F_{n-1}}+F_{n}\\ &=F_{n+1}+F_{n}\\ &=F_{n+2} \end{align}$
${\displaystyle\therefore \sum_{k=1}^{n}F_n =F_{n+2}-1 }$
黄金比とフィボナッチ数の関係
黄金比とフィボナッチ数には深い関係があり、無数の関係式が知られています。この記事では、次の関係を使います。
次数下げで黄金比の累乗をフィボナッチ数で表現する
$\varphi$ は二次方程式 $x^2=x+1$ の大きい方の解でもあるため、
$\varphi^2=\varphi+1$
の関係があります。
この両辺に順に $\varphi$ を乗じることで、次の一連の式を得ます。
$\varphi^2=\varphi+1$
$\varphi^3=\varphi^2+\varphi$
$\varphi^4=\varphi^3+\varphi^2$
$\varphi^5=\varphi^4+\varphi^3$
$\vdots$
これらの式の右辺について、$\varphi^2=\varphi+1$ を使って次数を下げることができます。$1$ 次式にまで次数を下げるとこうなります。
$\varphi^2=\varphi+1$
$\varphi^3=2\varphi+1$
$\varphi^4=3\varphi+2$
$\varphi^5=5\varphi+3$
$\vdots$
$\varphi^n=F_n\cdot\varphi+F_{n-1}$
フィボナッチ数が出てきましたね。
この関係は後で使います。
$\varphi^n=\varphi F_n+F_{n-1}$
隣接するフィボナッチ数の比は黄金比で近似できる
また、二次方程式 $x^2=x+1$ のもう一つの解を $\overline{\varphi}$ とすると、$\overline{\varphi}$についても
$\overline{\varphi}^2=\overline{\varphi}+1$
の関係がありますから同じことができて、
$\overline{\varphi}^n=\overline{\varphi}F_n+F_{n-1}$
両辺に $\varphi$ を乗じると
$\overline{\varphi}^n \varphi=\overline{\varphi}\varphi F_n+\varphi F_{n-1}$
解と係数の関係より $\overline{\varphi}\varphi=-1$ であることを使って整理すると
$F_n=\varphi F_{n-1}+\overline{\varphi}^{n-1}$
$\overline{\varphi}=-0.618\cdots$ ですから、第 $2$ 項の $\overline{\varphi}^{n-1}$ は $n$ が大きいときはほとんどゼロになります。
したがって、$n$ が大きいときは次のように近似することができます。
&&&lem 隣接するフィボナッチ数の比は黄金比で近似できる
$F_n\sim \varphi F_{n-1}$
$y=x/\varphi$上を点が移動したときに通過する直線の数
次に、直線 $y=x/\varphi$上を原点から正の方向に点が移動したとき、"$x=$整数" の直線と、"$y=$整数" の直線をそれぞれ何本通過するかを考えたいと思います。
いちいち書くのは面倒なので、ここからは「"$x=$整数" の直線と、"$y=$整数" の直線」を全部まとめて「直線群」と書きます。
そのための準備として、ちょっと唐突かもしれませんが、$y=x/\varphi$上を移動する点が直線群をちょうどフィボナッチ数回通過するときの座標をみてみましょう。
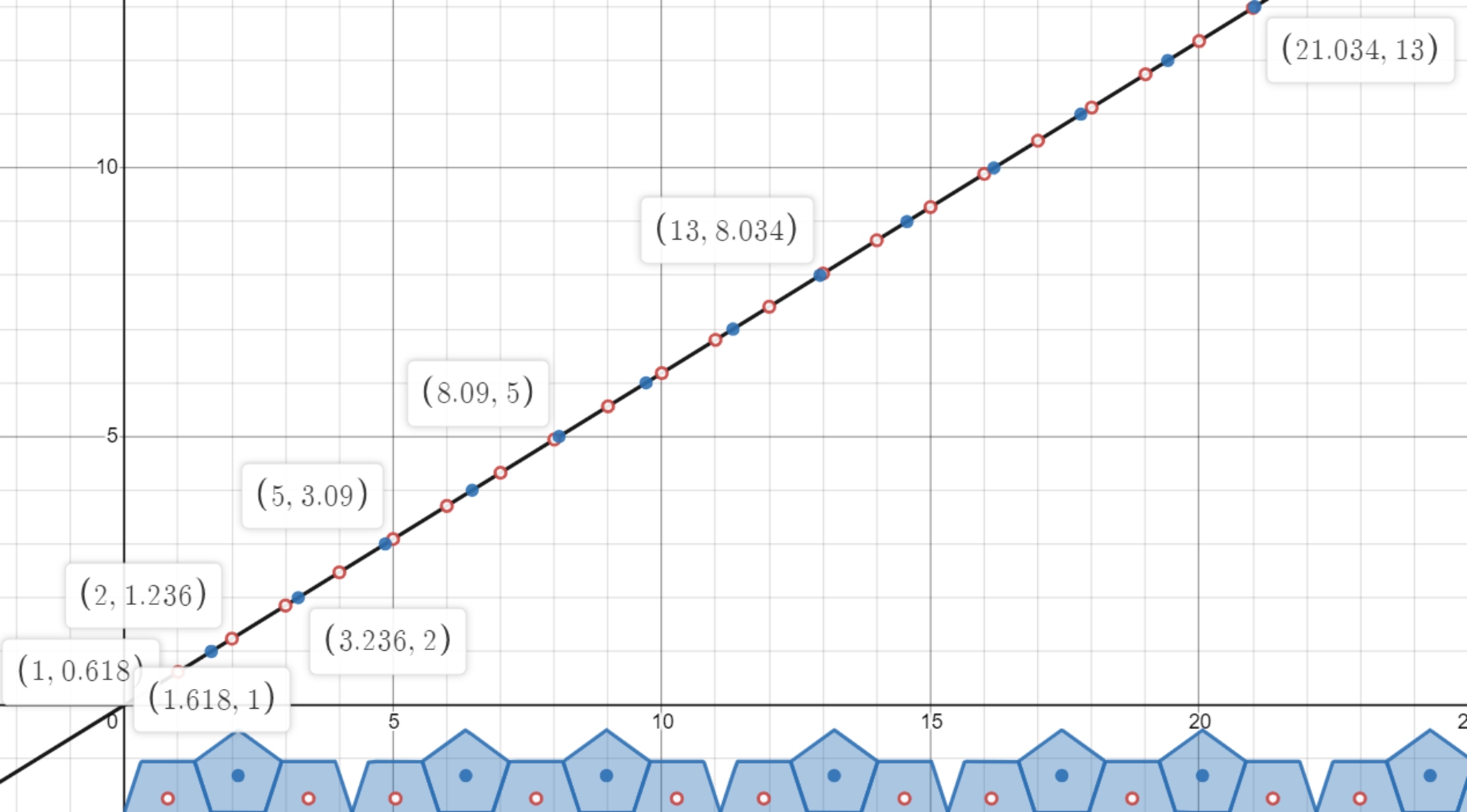交点の座標を調べる
| 回 | $x$ | $y$ |
|---|---|---|
| 1 | 1 | 0.618 |
| 2 | 1.618 | 1 |
| 3 | 2 | 1.236 |
| 5 | 3.236 | 2 |
| 8 | 5 | 3.09 |
| 13 | 8.09 | 5 |
| 21 | 13 | 8.034 |
※ 数値は近似値です
お気づきいただけましたでしょうか。
$x$座標、$y$座標ともにフィボナッチ数に近づいて行っていますね。
このことは、フィボナッチ数と黄金比の $F_{n+1}\sim \varphi F_n$ の関係から理解することができます。
つまり、$x$ 座標が $F_n$ のときの $y$ 座標は $\dfrac{F_n}{\varphi}\sim F_{n-1}$ となることから、直線 $y=x/\varphi$ は点 $\left(F_n,F_{n-1}\right)$ のすぐ近くを通ります。
すぐ近くを通るときは、"$x=$整数" の直線と "$y=$整数" の直線を短い間隔で通りますが、そのとき、"$x=$整数" の直線は $F_{n}$ 回目、"$y=$整数" の直線は $F_{n-1}$ 回目の通過になります。
このとき、直線群との通過回数の総数は $F_{n}+F_{n-1}=F_{n+1}$ 回になります。
【再掲】交点の座標を調べる
数式で表す
直線 $y=x/\varphi$上を原点から正の方向に点が移動していき、直線群を $n$ 回通過したときに、"$x=$整数" の直線をそれまでに通過した回数を $a(n)$ で、"$y=$整数" の直線をそれまでに通過した回数を $b(n)$ で表すことにします。
グラフを見て、通過する回数をカウントしてみるとこうなります。
| $n$ | $a(n)$ | $b(n)$ |
|---|---|---|
| 1 | 1 | 0 |
| 2 | 1 | 1 |
| 3 | 2 | 1 |
| 4 | 3 | 1 |
| 5 | 3 | 2 |
| 6 | 4 | 2 |
| 7 | 4 | 3 |
| 8 | 5 | 3 |
ここで、 "$x=$整数" の直線を $F_{n}$ 回、"$y=$整数" の直線を $F_{n-1}$ 回通過したときに直線群の通過の総回数が $F_{n+1}$ になることから、次の関係式が得られます。
$$ \begin{eqnarray} \left\{ \begin{array}{l} a(F_{n+1})=F_{n} \\ b(F_{n+1})=F_{n-1} \\ a(F_{n+1})+b(F_{n+1})=F_{n+1} \end{array} \right. \end{eqnarray} $$
となります。
見やすさのために添字を$1$つずらせば
$$ \begin{eqnarray} \left\{ \begin{array}{l} a(F_{n})=F_{n-1} \\ b(F_{n})=F_{n-2} \\ a(F_{n})+b(F_{n})=F_{n} \end{array} \right. \end{eqnarray} $$
となります。
また、最後の $2$回分の通過 ("$x=$整数" と"$y=$整数" を各$1$回ずつの通過) を引くと
&&&lem
$$
\begin{eqnarray}
\left\{
\begin{array}{l}
a(F_{n}-2)=F_{n-1}-1 \\
b(F_{n}-2)=F_{n-2}-1 \\
a(F_{n}-2)+b(F_{n}-2)=F_{n}-2
\end{array}
\right.
\end{eqnarray}
$$
という関係もありますね。
この関係式もあとで使います。
証明
これで準備がととのいました。
問題の図をもう一度見てみましょう。
【再掲】五芒星の足の間の星の数は1,2,3,5,8,……となっている
方針
正五角形の$1$辺の長さを $1$ とします。
図のように正五角形の列を左から $1,2,3,5,8,\ldots,F_k,\ldots$ 個ずつのまとまりで分けて、それぞれの左下の頂点から右下の頂点までの長さを $l(n)$ で表すことにします。
![この部分の長さを!FORMULA[93][1131688361][0]で表す](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20211103211725.jpg?alt=media)
この部分の長さを$l(n)$で表す
$1$辺の長さが $1$ の正五角形の対角線の長さは $\varphi$ になります(証明は省略しますが、正五角形内の相似な三角形を使えば容易に証明できます。)。
そうすると、$l(1)=\varphi$ であることがわかります。
そして隣り合う五芒星の相似比は $1:\varphi$ ですから、結局、次の式が成り立つことを示せばよいことになります。
$l(n)=\varphi^n$
証明
それではここから、$l(n)=\varphi^n$ であることを証明します。
まず、$l(n)$ の累計を $L(n)$ で表すことにします。式で表すと
${\displaystyle L(n)=\sum_{k=1}^{n}l(k)}$
$L(n)$ の対象となる正五角形の数は
${\displaystyle 1+2+3+5+8+\cdots+F_{n+1}=-1+\sum_{k=1}^{n+1}F_k=F_{n+3}-2}$
個あります。
したがって、 $L(n)$ は次のように表すことができます。
${\displaystyle \begin{align} L(n)&=\varphi\cdot a(F_{n+3}-2)+b(F_{n+3}-2)\\ &=\varphi\cdot (F_{n+2}-1)+(F_{n+1}-1)\\ \end{align}}$
この式と、と、先に示した黄金比とフィボナッチ数の関係式を使って $l(n)$ を計算するとこうなります。
$n\ge2$ のとき
${\displaystyle \begin{align} l(n)&=L(n)-L(n-1)\\ &=\left(\varphi\cdot (F_{n+2}-1)+(F_{n+1}-1)\right) -\left(\varphi\cdot (F_{n+1}-1)+(F_{n}-1)\right)\\ &=\varphi F_{n}+F_{n-1}\\ &=\varphi^n \end{align}}$
この式は $n=1$ の時も成り立つ。
したがって
$l(n)=\varphi^n$
まさにこれが証明すべきことでした! $\Box$
おわりに
今回のグラフ、よくみるといろいろなところにフィボナッチ数の漸化式のような関係が隠れていますので、探してみても楽しいと思います。
実は、今回の正五角形の配列は、今から３年少し前に、再帰的な敷き詰め方法を試行錯誤で探していた時に見つけたものでした。
うおお!
— ａｐｕ (@apu_yokai) August 23, 2018
作りたかったのはコレだ
辺の長さの比が黄金比の五芒星によるフィボナッチ・タイリング
完成してしまえばシンプルな法則で並べられるなあ。
黄金比とフィボナッチ数の相性は本当に素晴らしい! pic.twitter.com/1KFh2MkKMu
五芒星の再帰的敷き詰め
ところで、正五角形の列について、下向きの正五角形を $1$ 、上向きの正五角形を $0$ として並べるとこんな数列ができます。
$10110101101101011010110110101101\cdots$
この数列は RabBIT sequence と呼ばれているのですが、正五角形の配列を作った時はそのことを知らず、「こんな美しい配列には名前が付いているはずだ」と確信して検索して、実際にそれ(RabBIT sequence)を見つけることができたときは興奮しました。
なお、この配列は golden string 又は Fibonacci wordと呼ばれることもありますが、私はウサギとビットを組み合わせた RabBIT sequence という名前が気に入っています。
RabBIT sequence には面白い性質がいろいろありますので機会があればまたご紹介したいと思います。
参考文献
この記事を高評価した人
この記事に送られたバッジ
投稿者
