離散フーリエ変換で多角形の写像を分析する(GIF有)

はじめに
きっかけのツイート
実際にやってみる
$3$ 角形の場合
正 $\frac{N}{M}$ 角形の場合
正 $\frac{N}{M}$ 角形をアフィン変換した形の場合
対称性のない配置の場合はどうなる?
離散フーリエ変換で周期的な数列の一般項をサインカーブの和で表現する
頂点の座標を通過する関数を構成する
サインカーブの和を構成する
検算
$g_{k} (n)$ がサインカーブを描くことを確認する
対称性を使って必要な式の数を減らす
視覚化
$N$ 角形の $y$ 座標(又は $x$ 座標)は、 $⌊ \frac{N}{2} ⌋$ 個のサインカーブの和で表すことができる
$N$ 角形の $y$ 座標(又は $x$ 座標)は、正 $\frac{N}{M}$ 角形上を移動する点の座標の和で表すこともできる
多角形の頂点の位置ベクトルを移す写像
位置ベクトルを変換したあとの周波数ごとの振幅・位相の変化を調べる
振幅の変化を調べる
一般の $N$ 角形の場合
位相の変化を調べる
結論
おわりに
参考文献

高校数学解説

文献あり

離散フーリエ変換で多角形の写像を分析する(GIF有)

GIF,離散フーリエ変換,日曜数学会

766

はじめに

この記事は、2021年10月23日に開催された第 $22$ 回日曜数学会で私が発表した内容を記事にまとめたものです。

リンク: 日曜数学会

　離散フーリエ変換を使うと、任意の $N$ 角形の頂点の位置ベクトルを、 $⌊ \frac{N}{2} ⌋$ 個以下の(星型)正多角形の位置ベクトルの和として表すことができます。
そのことを応用して、任意の多角形にとある写像を続けた場合の収束先の図形を調べてみました。

星型正多角形の表記について

この記事では正 $N$ 角形の $M$ 個となりの頂点を順につないでできる星形多角形のことを分数を使って「正 $\frac{N}{M}$ 角形」と呼びます。

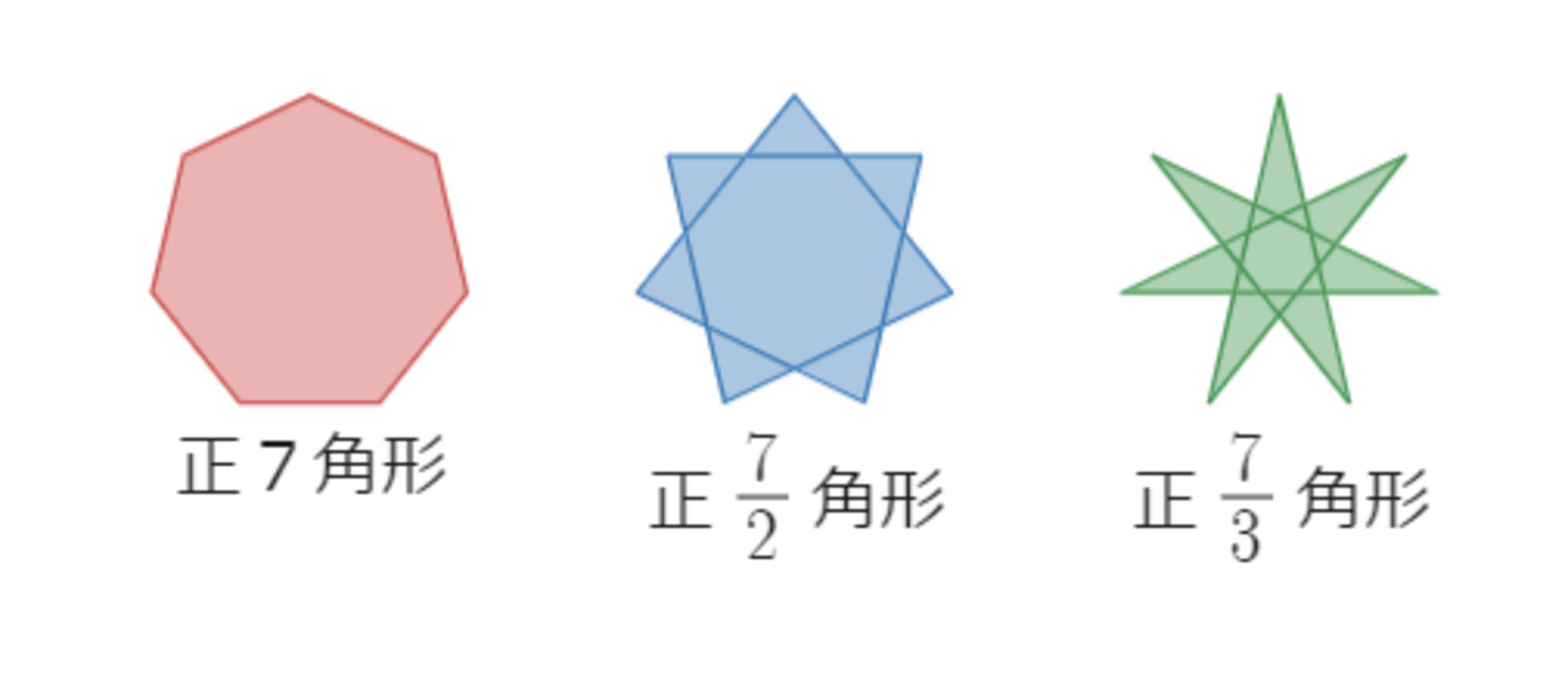正N/M角形

星型多角形の性質として、正 $\frac{N}{M}$ 角形の頂点を順になぞると、中心の周りを $M$ 周して元に戻ることを覚えておいてください。
別の言い方をすると、頂点を通過するごとに $\frac{M}{N}$ 回転しているとも言えます。

きっかけのツイート

そもそものきっかけは、Twitterでみかけた盛田みずすましさんのこちらのツイートでした。

この操作、繰り返すとどうなるでしょう？ pic.twitter.com/QFJvaJYl3i
— 盛田みずすまし (@nosiika) September 30, 2021

盛田みずすましさんのツイート

実際にやってみる

$3$ 角形の場合

適当に $3$ 角形を作ってこの変換をしてみると、 $2$ 回変換したところで $180$ 度回転し、 $4$ 回変換で元の形に戻ります。

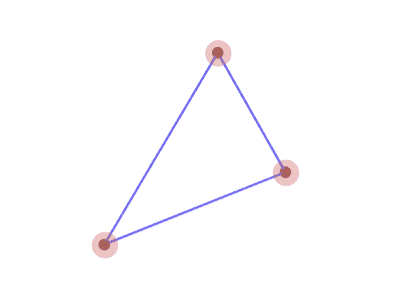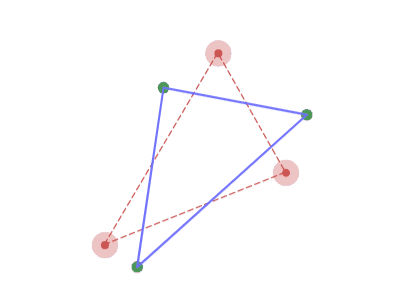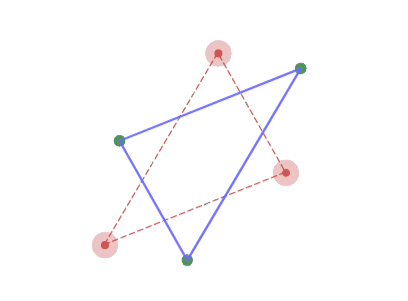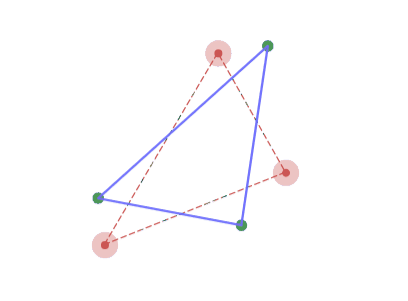3角形から始めると周期4でループする

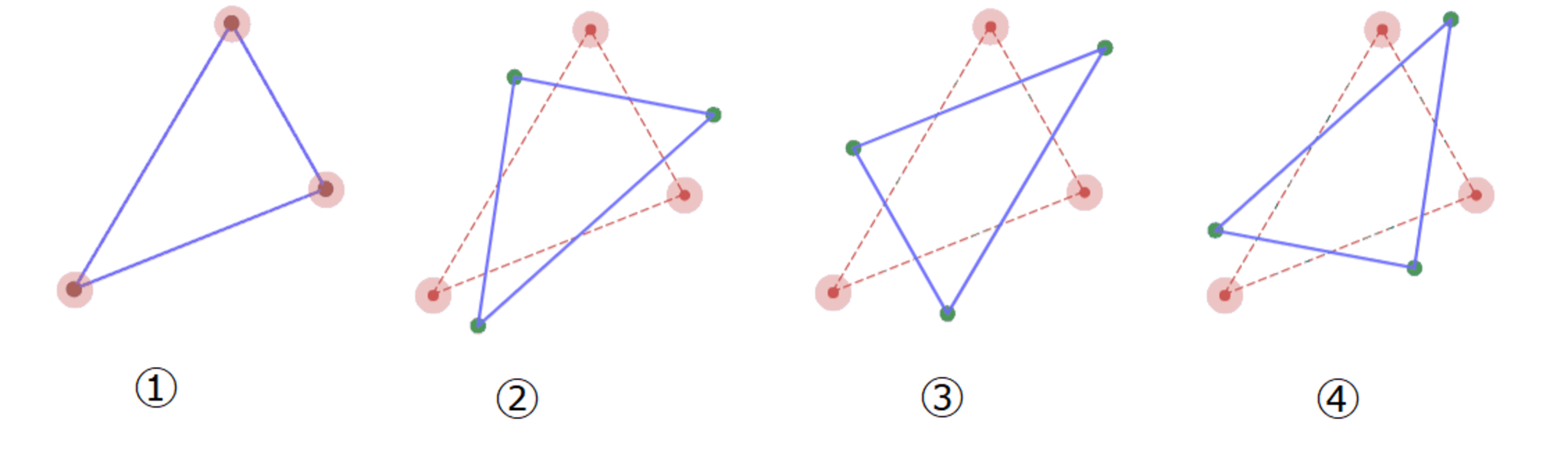①→②→③→④→①の順にループする

$3$ 角形の場合は $4$ 回でループしたということで、では $4$ 角形、 $5$ 角形、……の場合に同じ写像をしたらどんな風に変化するのか気になりますね。

正 $\frac{N}{M}$ 角形の場合

まずは、考えやすい、わかりやすい形から考えてみましょう。
正 $\frac{N}{M}$ 角形の場合で考えますと、対称性から、正 $\frac{N}{M}$ 角形の写像は正 $\frac{N}{M}$ 角形になるはずです。
実際にやってみると

正 !FORMULA[22][-397125431][0] 角形から始めたときも周期4でループする正 $\frac{N}{M}$ 角形から始めたときも周期4でループする

①→②→③→④→①の順にループする

となり、３角形の場合と同じように４回でループしました。
ただし、回転の方向は時計回りになる場合と反時計回りになる場合がありますね。

正 $\frac{N}{M}$ 角形をアフィン変換した形の場合

位置ベクトルの差で考える

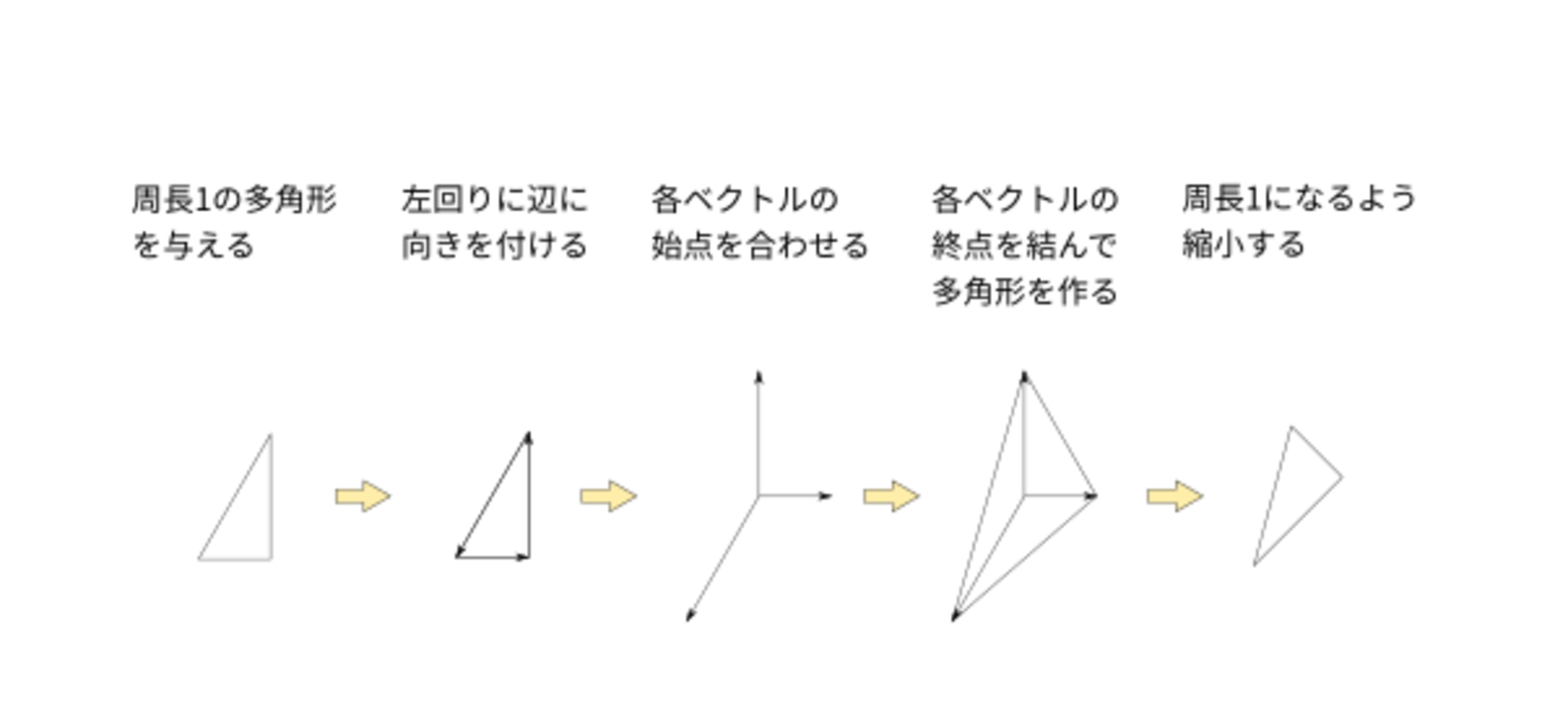
考えてみると、今回の写像は、元の頂点の位置ベクトルの差を新たな頂点の位置ベクトルとしてから全体を縮小する写像となっています。
写像の「形」だけに注目するならば、「全体を縮小する操作」を考える必要はありません。
そうすると、元の頂点の位置ベクトルの差を新たな頂点の位置ベクトルとする写像について考察すればよいことになります。

アフィン変換しても写像パターンは変わらない

さらに考えると、 $x$ 座標と $y$ 座標の計算は独立していますから、正 $\frac{N}{M}$ 角形をアフィン変換した形から始めても、アフィン変換する前の形の写像パターンと同じようにその写像パターンはループするはずです。

(※　アフィン変換……線型変換（回転、拡大縮小、剪断（せん断））と平行移動の組み合わせ)

実際にやってみると

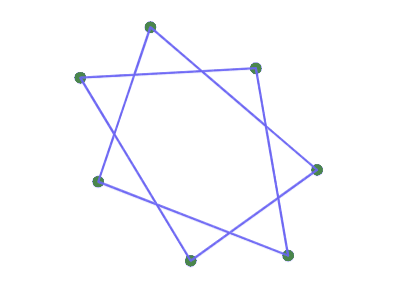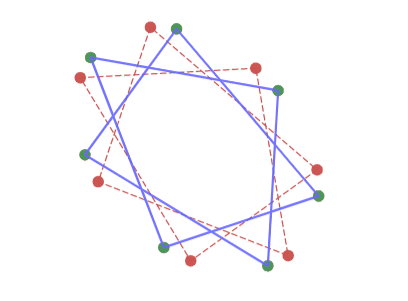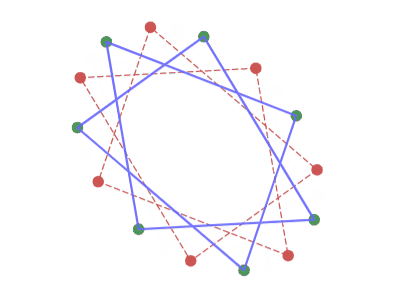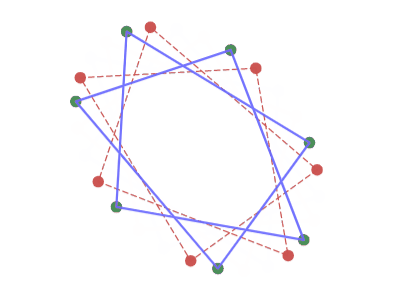アフィン変換しても変化の仕方は変わらない

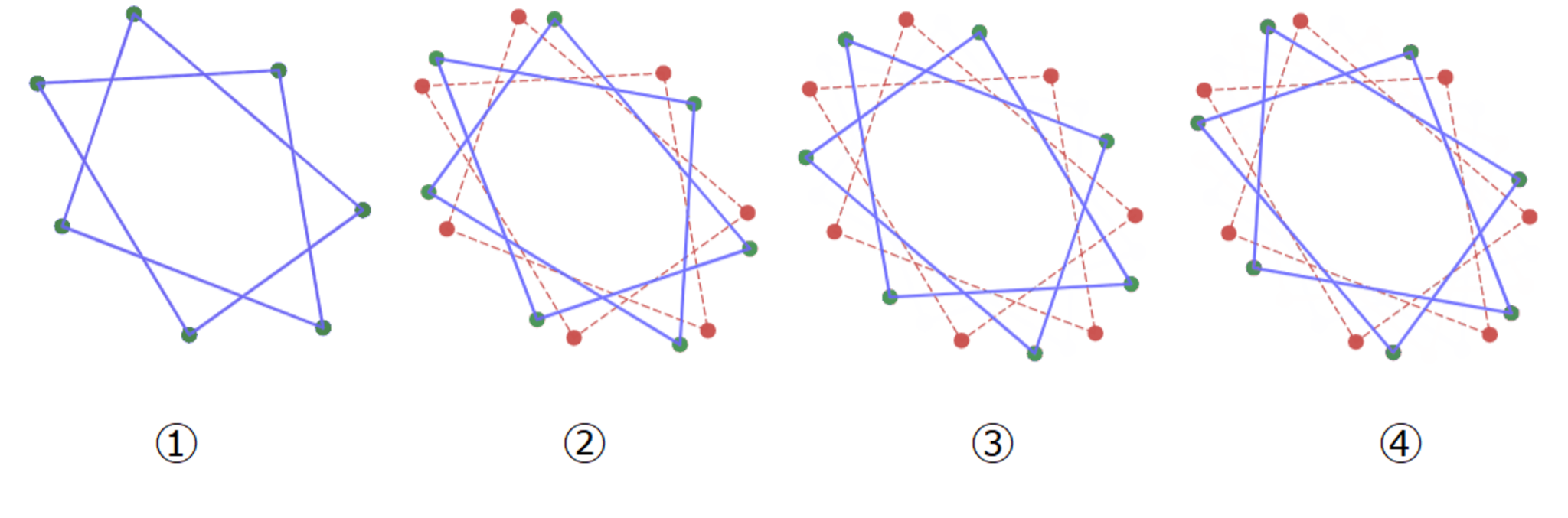①→②→③→④→①の順にループする

やはり４回でループしました。

対称性のない配置の場合はどうなる?

では、対称性のない、任意の配置から始めたら、どんな形に写像されるのでしょうか。
とりあえず、適当に点を配置して写像パターンを観察してみましょう。

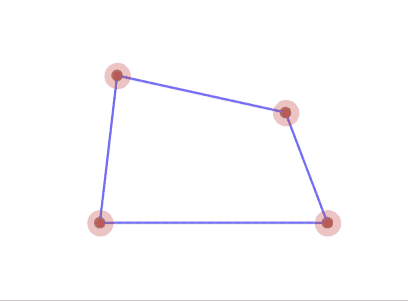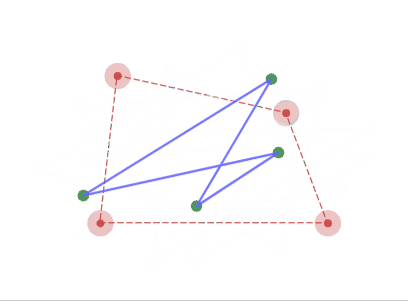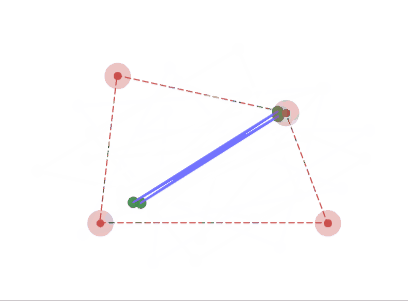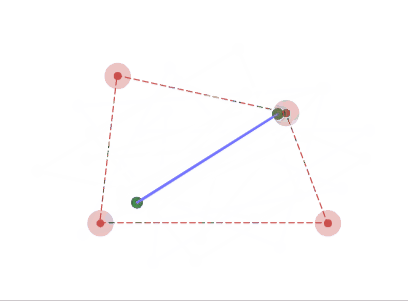4角形の場合、2点へと収束していく

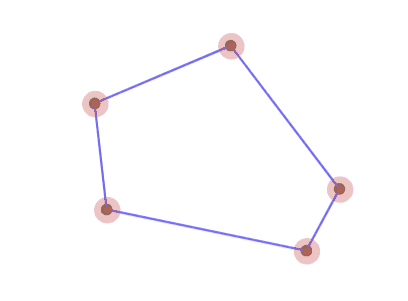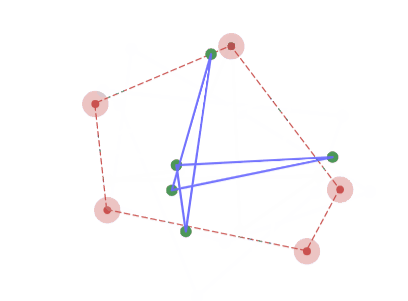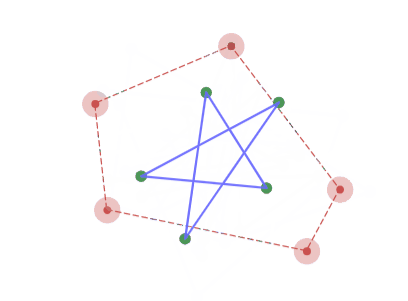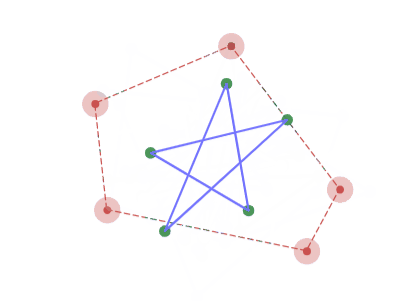5角形の場合、正5/2角形をアフィン変換した形へと収束していく

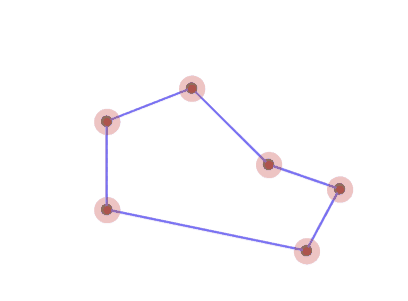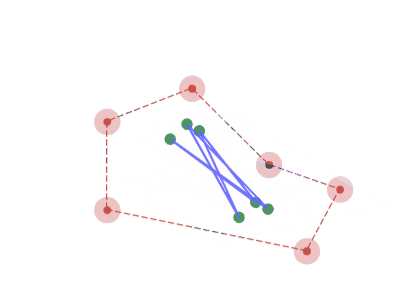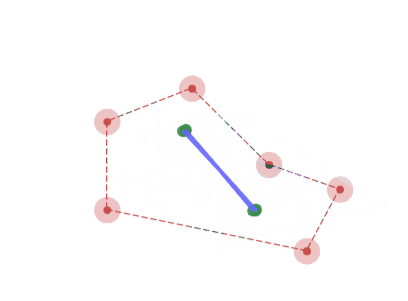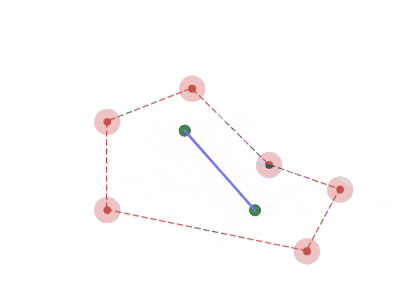6角形の場合、2点へと収束していく

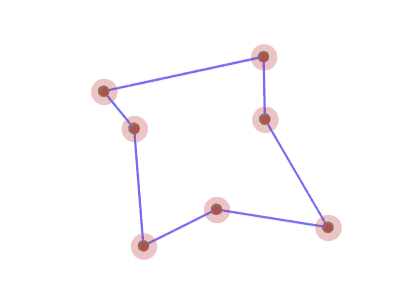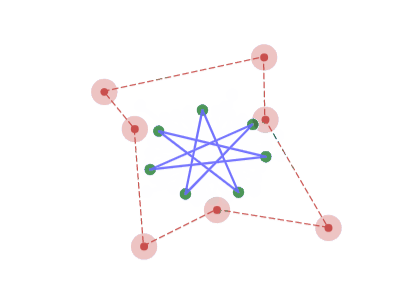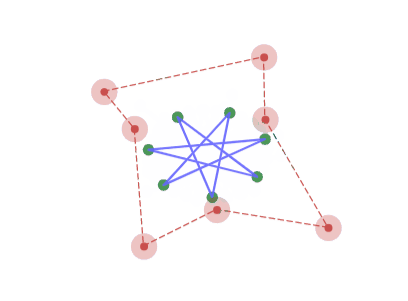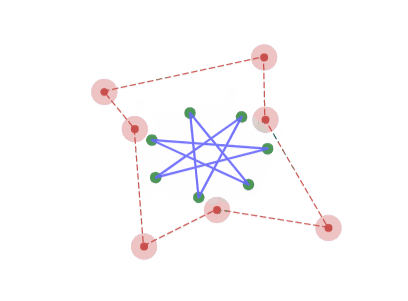7角形の場合、正7/3角形をアフィン変換した形に収束していく

任意の配置から始め、何度もこの写像を繰り返すと、最初のうちは複雑に変化しますが、やがて何らかの形に収束してループすることに気が付きます。

そして、星形多角形らしき形になってループするのは奇数角形のときだけで、偶数角形のときは２点へと収束していくことに気が付きます。

観察の結果、次のようなことが予想されます。

元の形と収束先の形についての予想

・正 $\frac{N}{M}$ 角形　→　正 $\frac{N}{M}$ 角形　(周期 $4$ でループ)

・正 $\frac{N}{M}$ 角形をアフィン変換した形　→　正 $\frac{N}{M}$ 角形をアフィン変換した形　(周期 $4$ でループ)

・どちらでもない偶数角形　→　 $2$ 点に収束

・どちらでもない奇数角形　→　最も鋭角な正 $\frac{N}{M}$ 角形をアフィン変換した形に収束

実は、これらの予想が正しいことが、離散フーリエ変換を使うとわかるんです!

では、ここからはそのことを説明したいと思います。

離散フーリエ変換で周期的な数列の一般項をサインカーブの和で表現する

Wikipediaでは、離散フーリエ変換について次のように説明しています。

離散フーリエ変換（りさんフーリエへんかん、英語: discrete Fourier transform、DFT）とは次式で定義される変換で、フーリエ変換に類似したものであり、信号処理などで離散化されたデジタル信号の周波数解析などによく使われる。また偏微分方程式や畳み込み積分の数値計算を効率的に行うためにも使われる。離散フーリエ変換は（計算機上で）高速フーリエ変換(FFT)を使って高速に計算することができる。(Wikipediaより)

なんだかよくわかりませんね。私にもよくわかりません。ただ、離散フーリエ変換を使うと次のようなことができることはわかっています。

離散フーリエ変換を使うと、 $N$ 個の点の $x$ 座標又は $y$ 座標を、「定数関数と $\frac{N}{2}$ 個以下の三角関数(サインカーブ)の和」で表すことができる！

そして、それを応用することにより先ほどの予想を証明できます。

頂点の座標を通過する関数を構成する

適当な $N$ 角形を作り、その $y$ 座標を

　　 $y_{0}, y_{1}, \dots, y_{N - 1}$

とおきます。次に、

　　 $f (j) = y_{j} (j \in {0, 1, 2, \dots, N - 1})$

を満たすような関数 $f (n)$ を考えます。

このような !FORMULA[44][1126147235][0] を構成したいこのような $f (n)$ を構成したい

離散フーリエ変換の考え方により、定数関数と $⌊ \frac{N}{2} ⌋$ 個以下のサインカーブの和でこのような $f (n)$ を構成することが可能です。

定数関数は平均値(重心とも解釈できます)を表します。
(以下の記事では定数関数についてはほとんど関係ないので適宜説明を省略します。)

　例えば頂点が $7$ 個の場合、周波数 $1$ ～ $3$ の $3$ つのサインカーブの和でこのような $𝑓 (𝑛)$ を構成できます。

次の図を見てください。

7つの座標の場合、3つのサインカーブの和で !FORMULA[52][1126147235][0] を構成することができる 7つの座標の場合、3つのサインカーブの和で $f (n)$ を構成することができる

図14で、黄色い線は周波数1、水色の線は周波数2、紫の線は周波数3のサインカーブで、それらの和が黒い点線となっています。
黒い点線が7つの点を通っていますね。
7つの $y$ 座標がどのような位置にあったとしても、このように $3$ つ以下のサインカーブの和でこの黒い点線のような関数を構成することができるのです!

ここで「周波数」とは、繰り返しの回数のことです。

　一般に、頂点数の半分以下のサインカーブの和でこのような関数を構成することができます。

サインカーブの和を構成する

それでは、これらのサインカーブはどのように構成すればいいのでしょうか。
具体的には離散フーリエ変換により次のようにして構成することができます。

$f (n) = \sum_{k = 0}^{N - 1} g_{k} (n)$

ただし
$g_{k} (n) = \frac{1}{N} \sum_{j = 0}^{N - 1} y_{j} \cos \frac{2 k π (n - j)}{N}$

上記の式を少し詳しく分析してみましょう。

$f (n)$ は、 $g_{0} (n)$ から $g_{N - 1} (n)$ までの $N$ 個の関数の和となっています。

実は、 $g_{0} (n)$ は定数関数であり、 $g_{1} (n)$ から $g_{N - 1} (n)$ までは、それぞれが周波数 $1$ ～ $N - 1$ のサインカーブを描く関数となっています。

つまり、たとえば $N = 7$ であれば、(定数関数と)周波数 $1$ ～ $6$ の $6$ つのサインカーブの和で $f (n)$ を構成できるというわけです。

……

ここで、「あれ？さっき、『頂点が $7$ 個の場合、周波数 $1$ ～ $3$ の $3$ つのサインカーブの和でこのような $𝑓 (𝑛)$ を構成できます。』って言ってなかったっけ?」と思われた方がいるかもしれません。

そのカラクリは後程説明しますので、まずは本当にこの式が $f (j) = y_{j}$ になるのか検算してみましょう。

検算

検算してみましょう。

$\begin{aligned} f (n) & = \sum_{k = 0}^{N - 1} (\frac{1}{N} \sum_{j = 0}^{N - 1} y_{j} \cos \frac{2 k π (n - j)}{N}) \\ = \frac{1}{N} \sum_{j = 0}^{N - 1} y_{j} \sum_{k = 0}^{N - 1} \cos \frac{2 k π (n - j)}{N} \end{aligned}$

ここで $| n - j | < N$ より

$\begin{aligned} \sum_{k = 0}^{N - 1} \cos \frac{2 k π (n - j)}{N} & = {\begin{cases} N & for n = j \\ 0 & for n \neq j \end{cases} \end{aligned}$

ですから、

$f (j) = y_{j}$

となることが確かめられました。

$g_{k} (n)$ がサインカーブを描くことを確認する

ここまで、天下りに「 $g_{k} (n)$ がサインカーブを描く」ことを前提とした説明をしてきましたが、「本当にサインカーブになるのかしら」と疑問に思われる方もいると思いますので、本当にサインカーブになることを確認したいと思います。

$g_{k} (n) = \frac{1}{N} \sum_{j = 0}^{N - 1} y_{j} \cos \frac{2 k π (n - j)}{N}$

$\cos$ はサインカーブを描くことは言うまでもないですが、 $g_{k} (n)$ は $N$ 個の $\cos$ の和、すなわちサインカーブの和となっています。

それぞれのサインカーブの振幅(波の大きさ)や位相(波の頂点の位置)はバラバラですが、周波数は同じになっています。

これらのサインカーブたちの和もまたサインカーブとなることは、簡単に証明できます。しかも、三角関数の公式を使わずに証明できます!　次の図を見てください。

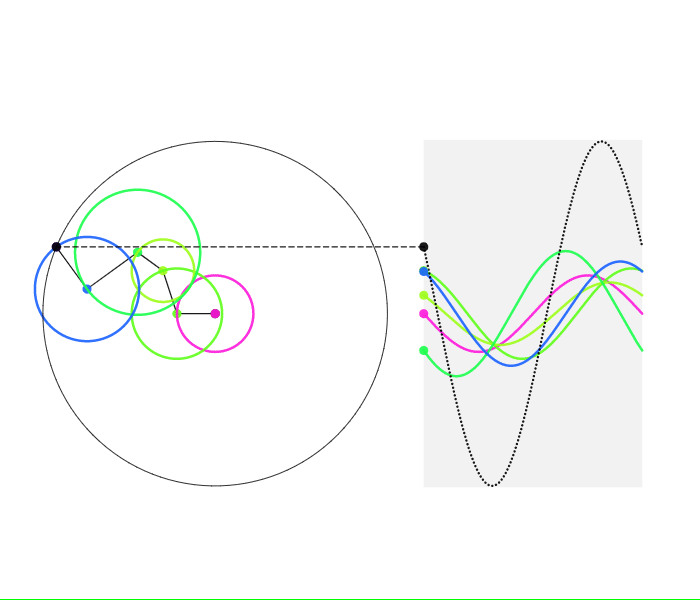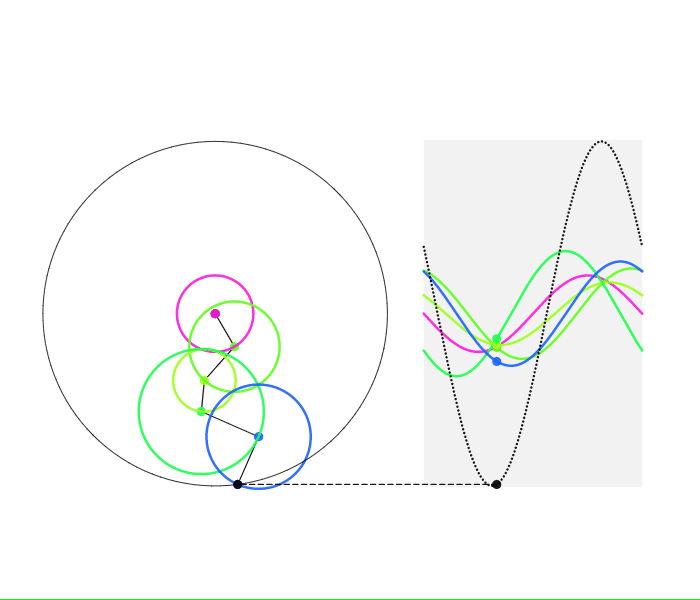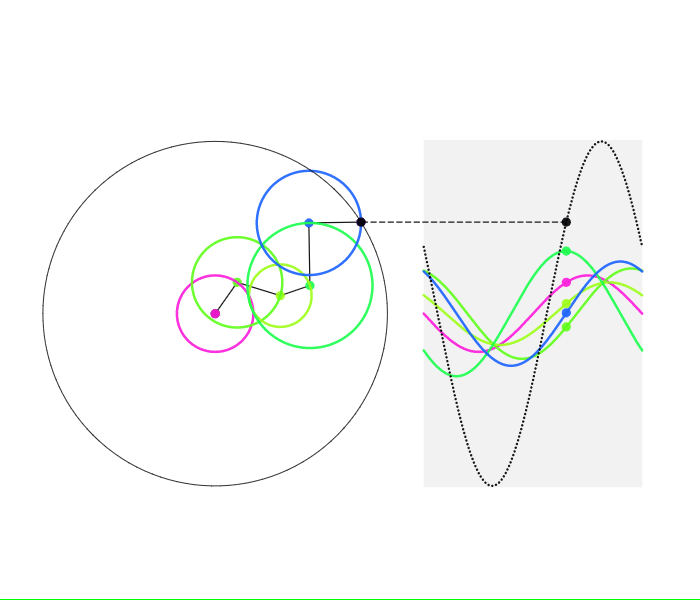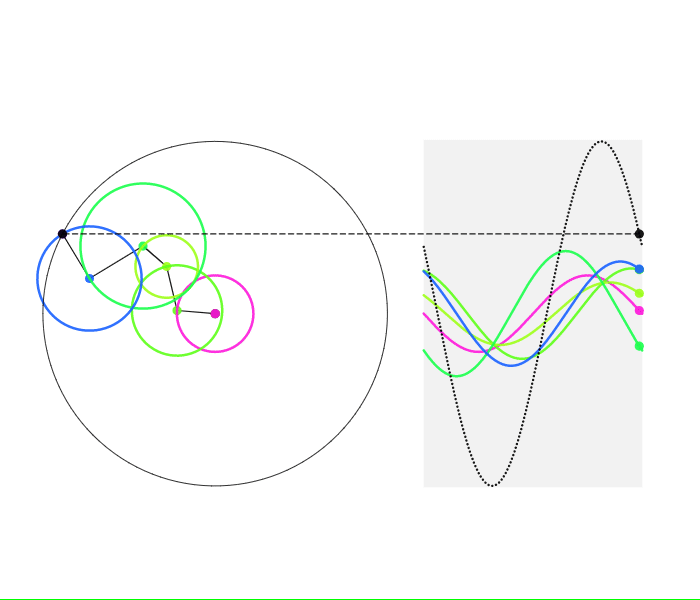周波数が同じサインカーブの和は１つのサインカーブとなる

この図を見れば、複数のサインカーブの周波数が同じならば、振幅や位相がずれていても、総和が１つのサインカーブとなることがお判りいただけることと思います。

対称性を使って必要な式の数を減らす

例えば $7$ 角形の場合、その頂点座標( $x$ か $y$ のどちらか)を $f (n)$ で表そうとした場合、ここまでの方法だと、 $1$ つの定数関数 $g_{0} (n)$ と、周波数 $1$ ～ $6$ のサインカーブの形になる $g_{1} (n) ～ g_{6} (n)$ の和で構成することができるのでした。

実は、周波数 $4$ ～ $6$ の式 $g_{4} (n) ～ g_{6} (n)$ は、それぞれ周波数 $3$ ～ $1$ の式 $g_{3} (n) ～ g_{1} (n)$ に置き換えても問題ありません。

&&&ex　 $7$ 角形の場合
$N = 7, n \in {0, 1, \dots, 6}$ のとき、

$g_{4} (n) = g_{3} (n)$
$g_{5} (n) = g_{2} (n)$
$g_{6} (n) = g_{1} (n)$

したがって、次のように式を簡単にすることができます。

&&&ex　 $7$ 角形の場合

$f (n) = g_{0} (n) + g_{1} (n) + g_{2} (n) + g_{3} (n) + g_{4} (n) + g_{5} (n) + g_{6} (n)$

又は

$f (n) = g_{0} (n) + 2 g_{1} (n) + 2 g_{2} (n) + 2 g_{3} (n)$

どちらの式を使っても
$f (j) = y_{j}$

グラフで確認してみましょう。
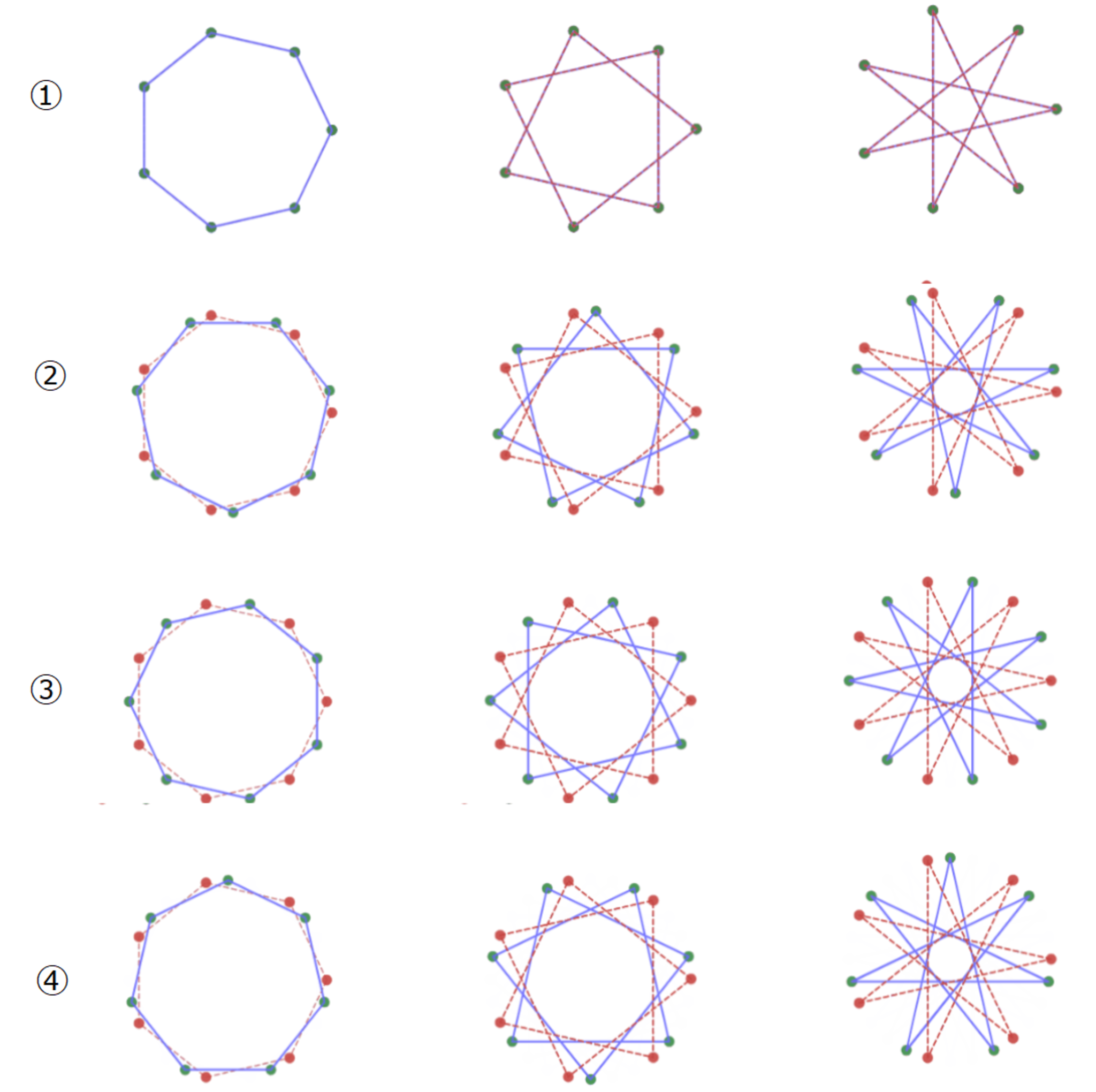
周波数 $1$ ～ $6$ のサインカーブの和で構成するとこんな感じにゴチャゴチャしていますが……

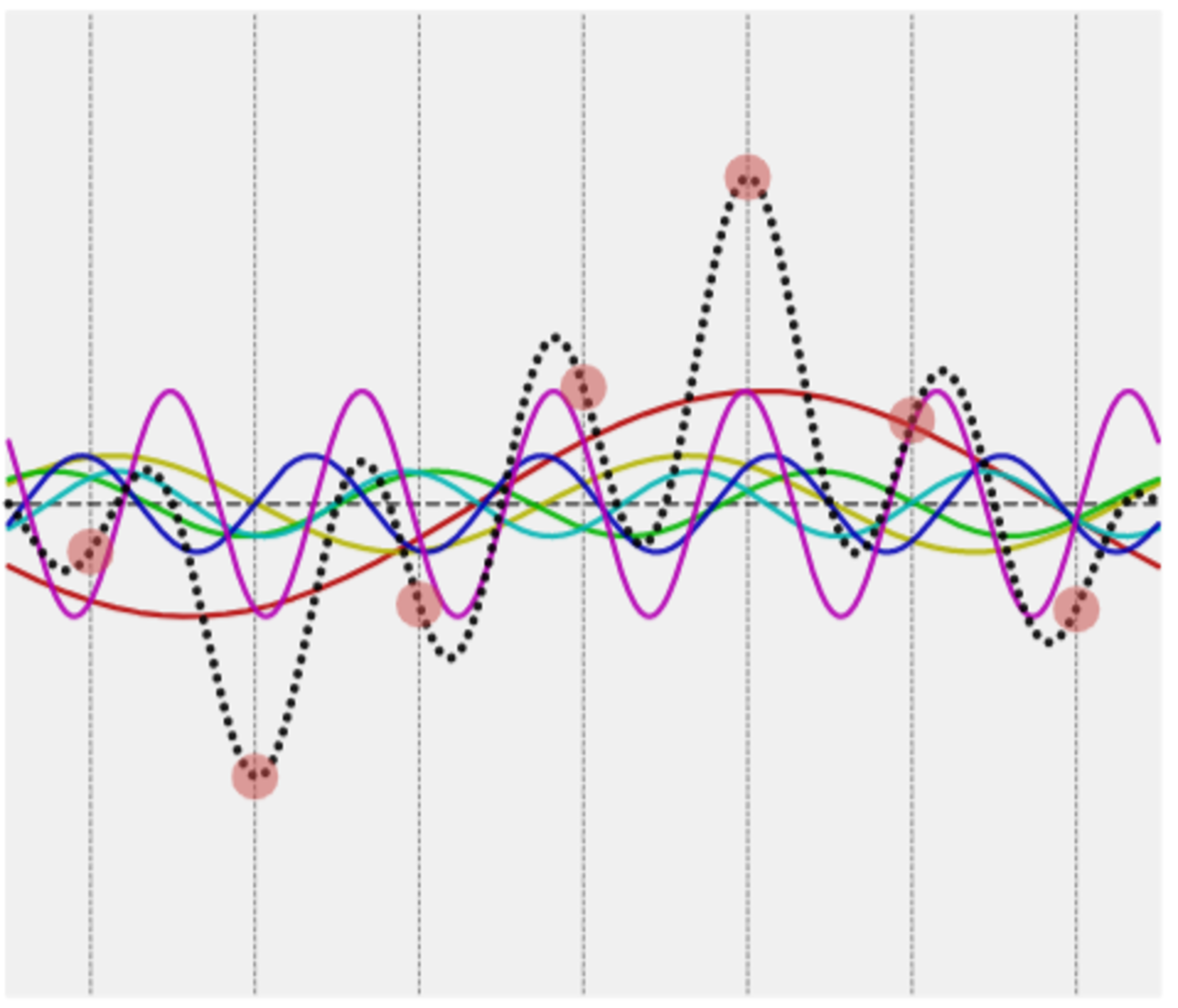7 頂点の場合、周波数 k と周波数(7-k)のサインカーブは同じ点を通っている

ちょっと見づらいかもしれませんが、周波数 $k$ と周波数 $(7 - k)$ のサインカーブは同じ点を通っていることを確認してみてください。

同じ点を通っているから、周波数 $(7 - k)$ のサインカーブは周波数 $k$ のサインカーブに置き換えることができるのです。
置き換えた周波数のサインカーブは、振幅が2倍になることになります。

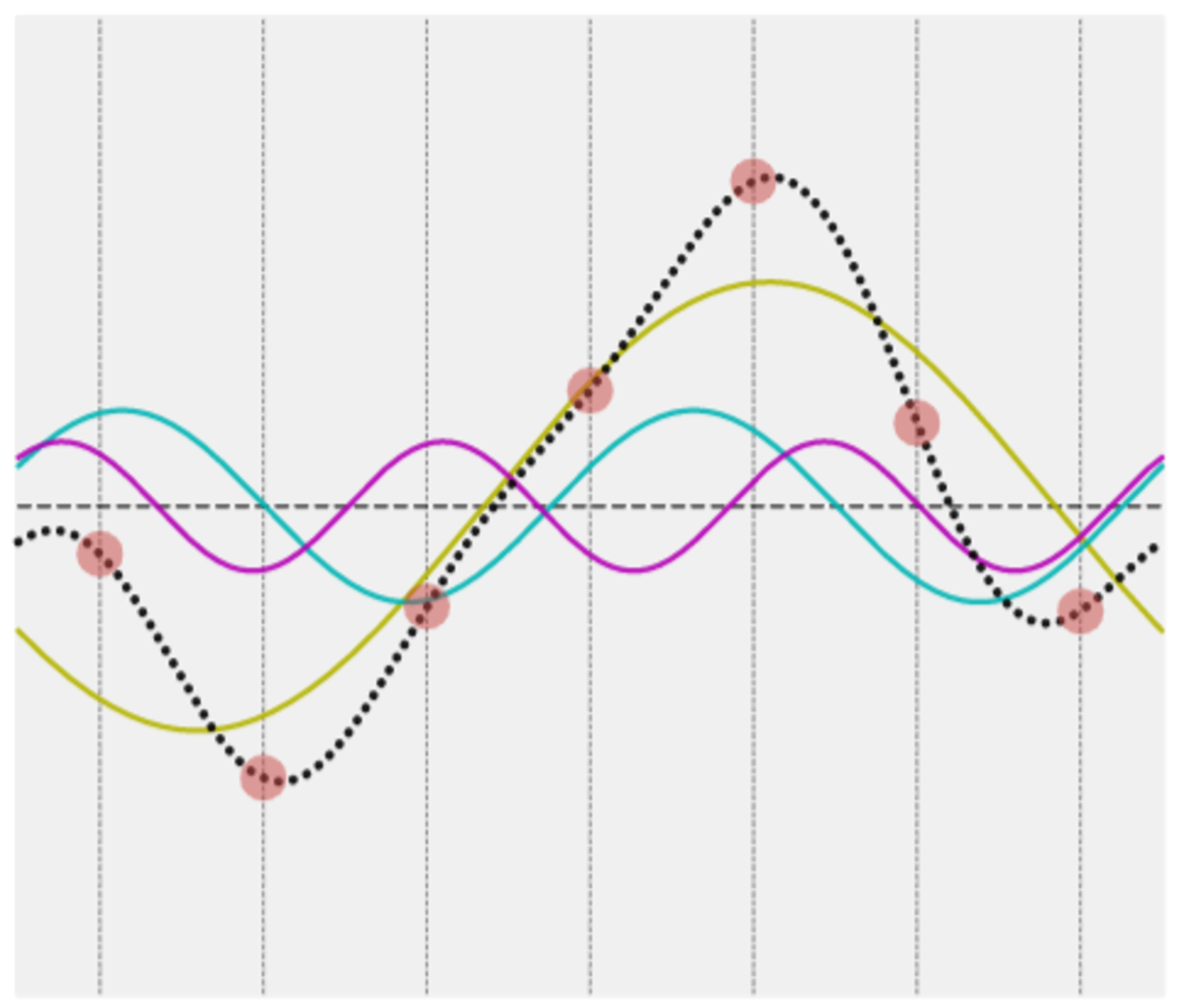したがって、周波数(7-k)を周波数kのサインカーブに置き換えることができる

周波数 $1$ ～ $3$ のサインカーブの和で構成するとシンプルになってカッコイイですね!

一般に、 $n \in {0, 1, \dots, N - 1}$ に対し、
$g_{k} (n) = g_{N - k} (n)$ が成り立つため、このようなことができます。

$\begin{aligned} g_{N - k} (n) & = \frac{1}{N} \sum_{j = 0}^{N - 1} y_{j} \cos \frac{2 (N - k) π (n - j)}{N} \\ = \frac{1}{N} \sum_{j = 0}^{N - 1} y_{j} \cos (2 π (n - j) - \frac{2 k π (n - j)}{N}) \\ = \frac{1}{N} \sum_{j = 0}^{N - 1} y_{j} \cos \frac{2 k π (n - j)}{N} \\ = g_{k} (n) \end{aligned}$

「周波数の高い成分を低い成分に置き換えることに何の意味があるの?」と思われるかもしれませんが、このあとの議論がしやすくなるので以降は置き換えた後の式で考えます。

(余談ですが、視覚化する際には、周波数の高い成分を少なくした方が圧倒的にスマートに見えるので重要なテクニックとなります。)

視覚化

$N$ 角形の $y$ 座標(又は $x$ 座標)は、 $⌊ \frac{N}{2} ⌋$ 個のサインカーブの和で表すことができる

$x$ 座標、 $y$ 座標をそれぞれサインカーブに分解すれば、次のように視覚化することができます。

x,y座標を回転する円周上の点の座標の和で表すことができる

このような視覚化をしている人はたまに見かけます。

$N$ 角形の $y$ 座標(又は $x$ 座標)は、正 $\frac{N}{M}$ 角形上を移動する点の座標の和で表すこともできる

今回、今から説明することをわかりやすくするために、先ほどの図をアレンジしてちょっと新しい視覚化を考えました。こんな感じです。

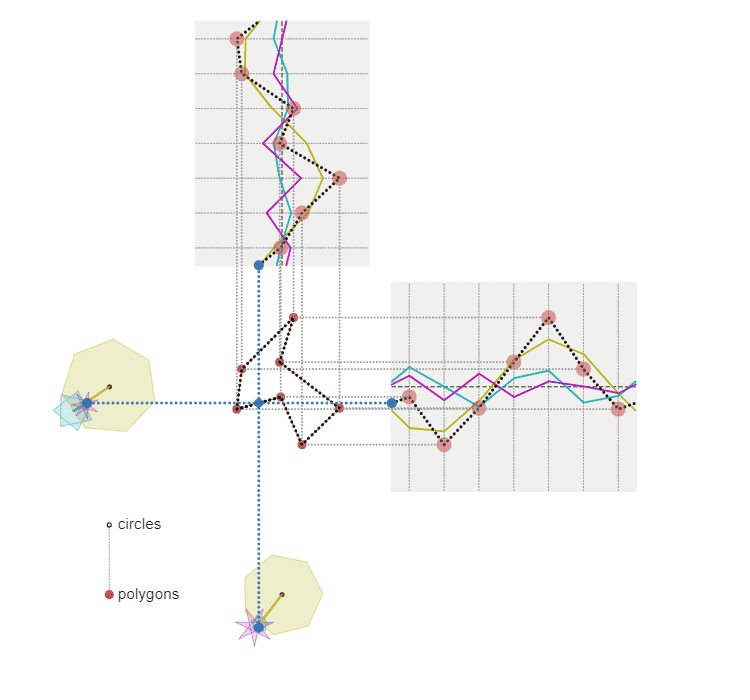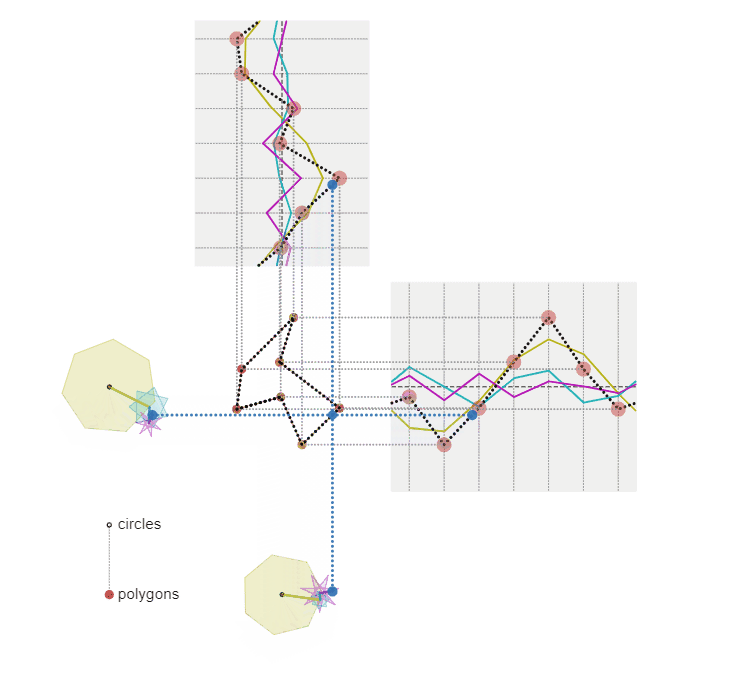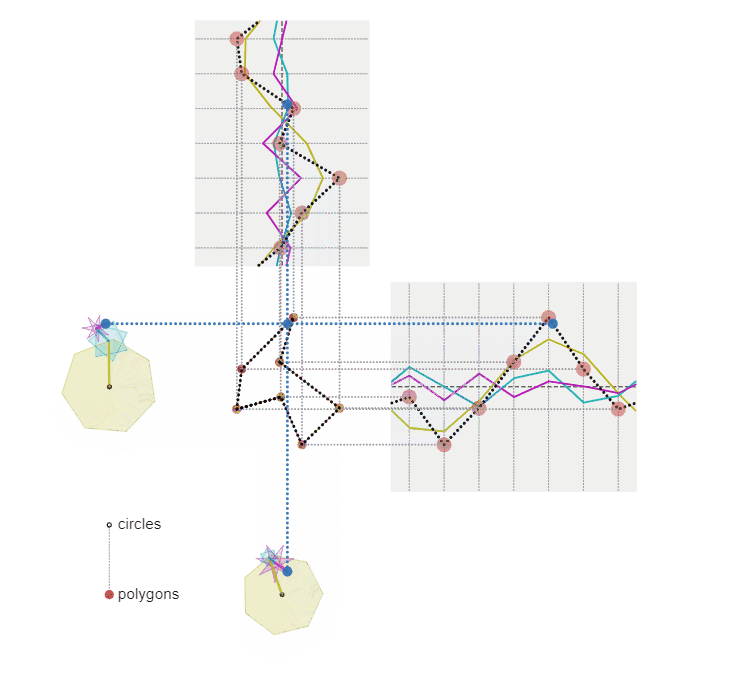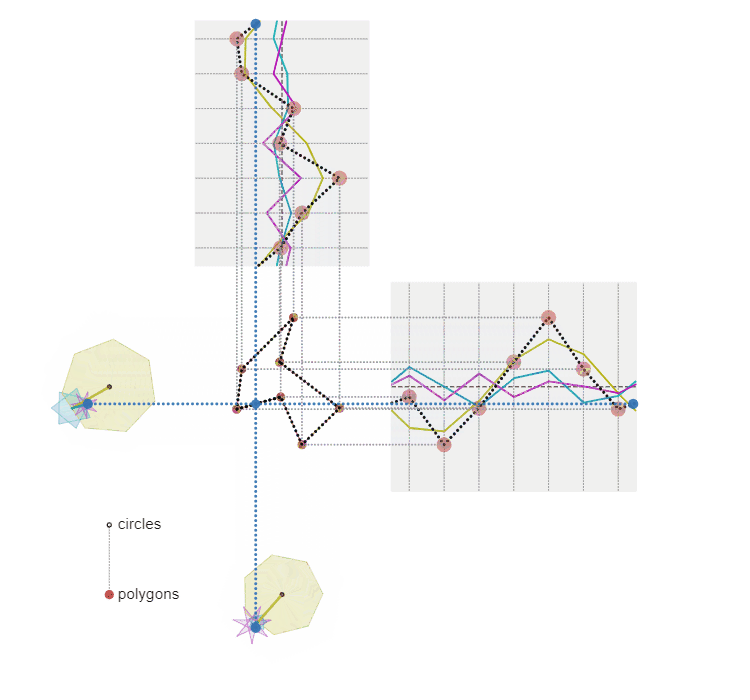x,y座標を正N/M角形上を移動する点の座標の和で表すこともできる

先ほどの図と見比べていただくと、それぞれの座標をつないでいたサインカーブを折れ線にしただけです。例えば頂点数 $7$ 、周波数 $3$ のサインカーブは、 $1$ 周期に $3$ 周する点の軌跡を $7$ 等分した位置を通過することから、正 $\frac{7}{3}$ 角形の頂点と考えることもできるので、このような視覚化が可能となるわけです。

多角形の頂点の位置ベクトルを移す写像

今回の写像で新たな多角形を作ると、新たな多角形の頂点の $y$ 座標は元の多角形の頂点の $y$ 座標の差ですから

$(y_{1} - y_{0}), (y_{2} - y_{1}), \dots, (y_{0} - y_{N - 1})$

となります。(縮小する操作は考えていないことに注意)

先ほどと同様に

　　 $f_{s} (0) = (y_{1} - y_{0}), f_{s} (1) = (y_{2} - y_{1}), \dots, f_{s} (N - 1) = (y_{0} - y_{N - 1})$

を満たすような関数 $f_{s} (n)$ を考え、サインカーブの和でこのような $f_{s} (n)$ を構成します。
なお、以下では表記を簡単にするために添字は $\mod N$ で考えてください。
三角関数の公式を使いながら変形していくと

$f_{s} (n) = \sum_{k = 0}^{N - 1} g_{s k} (n)$

$\begin{aligned} g_{s k} (n) & = \frac{1}{N} \sum_{j = 0}^{N - 1} (y_{j + 1} - y_{j}) \cos \frac{2 k π (n - j)}{N} \\ = \frac{1}{N} \sum_{j = 0}^{N - 1} y_{j + 1} \cos \frac{2 k π (n - j)}{N} - \frac{1}{N} \sum_{j = 0}^{N - 1} y_{j} \cos \frac{2 k π (n - j)}{N} \\ = \frac{1}{N} \sum_{j = 0}^{N - 1} y_{j} \cos (\frac{2 k π (n - j)}{N} + \frac{2 k π}{N}) - \frac{1}{N} \sum_{j = 0}^{N - 1} y_{j} \cos \frac{2 k π (n - j)}{N} \\ = \frac{1}{N} \sum_{j = 0}^{N - 1} y_{j} (\cos (\frac{2 k π (n - j)}{N} + \frac{2 k π}{N}) - \cos \frac{2 k π (n - j)}{N}) \\ = \frac{1}{N} \sum_{j = 0}^{N - 1} y_{j} (- 2 \sin (\frac{k π}{N}) \sin (\frac{2 k π (n - j)}{N} + \frac{k π}{N})) \\ = \frac{1}{N} \sum_{j = 0}^{N - 1} y_{j} 2 \sin (\frac{k π}{N}) \cos (\frac{2 k π (n - j)}{N} + \frac{k π}{N} + \frac{π}{2}) \end{aligned}$

という形にすることができます。
式の形から、それぞれの $g_{s k} (n)$ がどんな関数になるかを分析すると、

$k = 0$ のとき

$g_{s 0} (n) = 0$ なので新たな多角形の重心は原点になります。

$k \neq 0$ のとき

$g_{k} (n)$ と $g_{s k} (n)$ の式の形を見比べてみましょう。

$g_{k} (n) = \frac{1}{N} \sum_{j = 0}^{N - 1} y_{j} \cos \frac{2 k π (n - j)}{N}$

$g_{s k} (n) = \frac{1}{N} \sum_{j = 0}^{N - 1} y_{j} \underset{振幅に寄与}{\underset{⏟}{2 \sin \frac{k π}{N}}} \cos (\frac{2 k π (n - j)}{N} \underset{位相に寄与}{\underset{⏟}{+ \frac{k π}{N} + \frac{π}{2}}})$

$k \neq 0$ のとき、 $g_{s k} (n)$ は $g_{k} (n)$ の振幅を $2 \sin \frac{k π}{N}$ 倍にして、位相を
$(\frac{k π}{N} + \frac{π}{2})$ ずらしたものになっていることが分かります。

見やすくするために、 $k \neq 0$ のときの $g_{s k} (n)$ と $g_{k} (n)$ の位相のズレを $α_{k} (= \frac{1}{2} + \frac{N}{4 k})$ で表すと、次のような関係であることがわかります。

$g_{s k} (n) = \underset{振幅に寄与}{\underset{⏟}{2 \sin \frac{k π}{N}}} \cdot g_{k} (n \underset{位相に寄与}{\underset{⏟}{+ α_{k}}})$

位置ベクトルを変換したあとの周波数ごとの振幅・位相の変化を調べる

振幅の変化を調べる

一般の場合を考える前に、具体的な方がイメージしやすいと思いますので、 $7$ 角形の場合で考えてみましょう。
変換前の $7$ 角形の座標( $x$ 又は $y$ )を離散フーリエ変換の方法で表すと、周波数 $1$ ～ $3$ のサインカーブの和の形で表すことができたのでした。

変換後の $7$ 角形の座標( $x$ 又は $y$ )も、周波数 $1$ ～ $3$ のサインカーブの和の形で表すことができますが、位相がズレ、振幅は

周波数 $1$ のサインカーブの振幅は $2 \sin \frac{π}{7}$ 倍に、
周波数 $2$ のサインカーブの振幅は $2 \sin \frac{2 π}{7}$ 倍に、
周波数 $3$ のサインカーブの振幅は $2 \sin \frac{3 π}{7}$ 倍に、

それぞれ拡大又は縮小されることになります。

今回は、図形の形に注目していますので、比で考えればよく、もとの $7$ 角形の周波数 $1$ ～ $3$ のサインカーブの振幅の比を

$a_{1} : a_{2} : a_{3}$

とすると、写像の振幅の比は

$a_{1} \sin \frac{π}{7} : a_{2} \sin \frac{2 π}{7} : a_{3} \sin \frac{3 π}{7}$

へと変化することが分かります。

写像を繰り返し適用したあとの収束先

では、この写像を繰り返すと何がおきるでしょうか。 $t$ 回繰り返した後、周波数 $1$ ～ $3$ のサインカーブの振幅の比は

$a_{1} {(\sin \frac{π}{7})}^{t} : a_{2} {(\sin \frac{2 π}{7})}^{t} : a_{3} {(\sin \frac{3 π}{7})}^{t}$

へと変化します。

下図のように、 $\sin \frac{π}{7} < \sin \frac{2 π}{7} < \sin \frac{3 π}{7}$ ですから、図形の形だけに注目すると、写像を繰り返すごとに、相対的に周波数の高い成分だけが残ることになります。

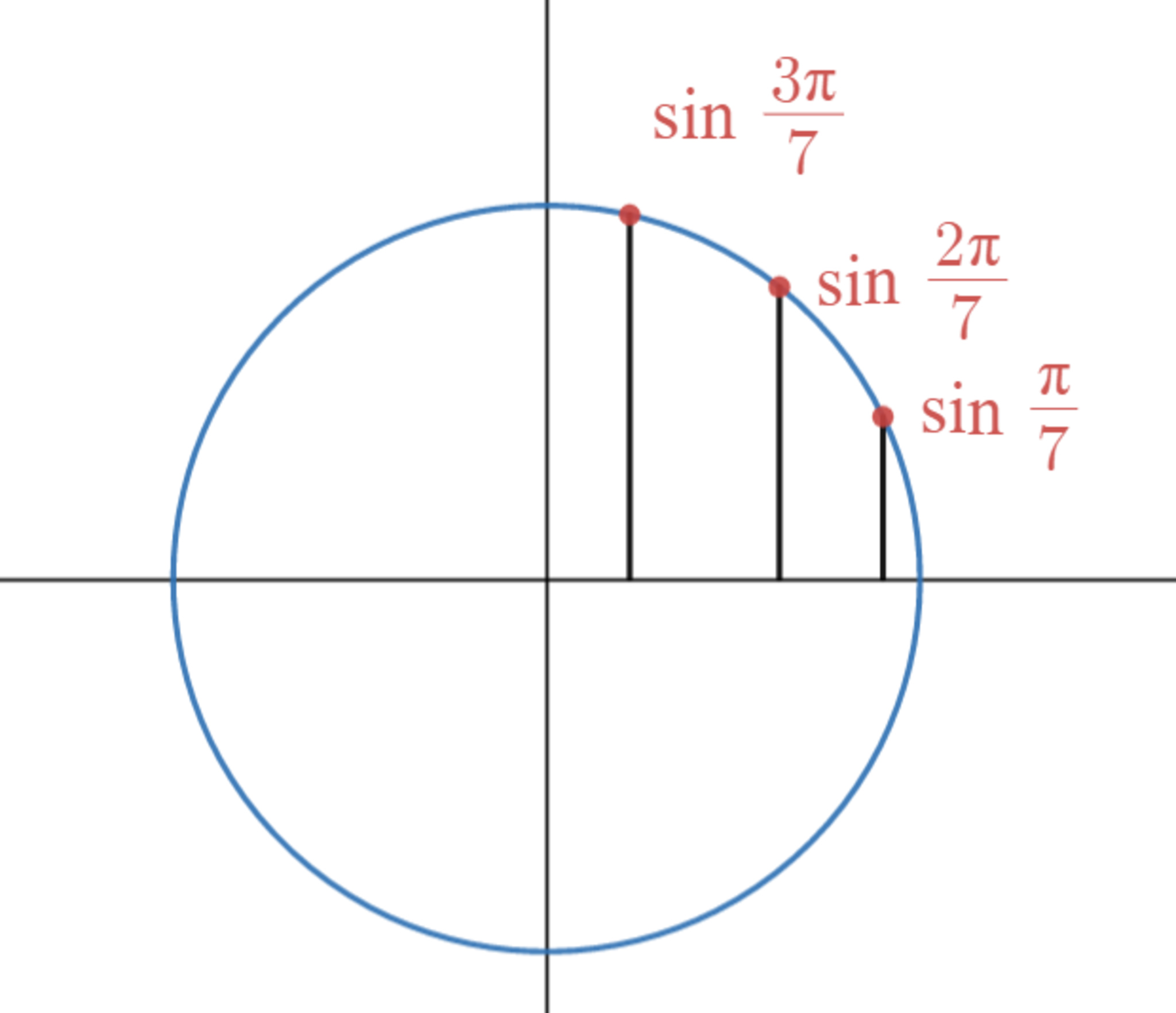大きさの比較

最終的には、周波数 $3$ の成分だけが残り、周波数 $2$ 以下は限りなく $0$ へ近づいていくことになります。

周波数の低い成分の振幅は !FORMULA[196][36120][0] に近づいていく周波数の低い成分の振幅は $0$ に近づいていく

例外について

ただし、例外があることに注意が必要です。
ここまでの議論は、もともとの $7$ 角形について「周波数 $3$ の成分が $0$ ではない」ことを前提としていました。もし、「周波数 $3$ の成分が $0$ である」ならば、 $0$ に何をかけても $0$ ですから、収束先の形にも周波数 $3$ の成分は含まれません。

このように、任意の $7$ 角形に写像を繰り返したとき、厳密には周波数 $3$ の成分が残るとは限らず、「振幅が $0$ ではないもののうち最も高い周波数」の成分が残るということになります。

一般の $N$ 角形の場合

ここまで、イメージしやすいように $7$ 角形の例で考えてきましたが、一般の $N$ 角形でも同じ議論ができます。

つまり、 $N$ 角形の場合は周波数 $1$ ～ $⌊ \frac{N}{2} ⌋$ のサインカーブの和として座標を表す関数 $f (n)$ を構成することができ、もとの $N$ 角形の周波数 $1$ ～ $⌊ \frac{N}{2} ⌋$ のサインカーブの振幅の比を

$a_{1} : a_{2} : \dots : a_{⌊ N / 2 ⌋}$

とすると、

$t$ 回の写像の後の周波数 $1$ ～ $⌊ \frac{N}{2} ⌋$ のサインカーブの振幅の比は

$a_{1} {(\sin \frac{π}{N})}^{t} : a_{2} {(\sin \frac{2 π}{N})}^{t} : \dots : a_{⌊ N / 2 ⌋} {(\sin \frac{⌊ \frac{N}{2} ⌋ π}{N})}^{t}$

に変化します。そして、

$\sin \frac{π}{N} < \sin \frac{2 π}{N} < \dots < \sin \frac{⌊ \frac{N}{2} ⌋ π}{N}$

ですから、操作を繰り返すと「振幅が $0$ でないもののうち最も高い周波数」の成分だけが残ることが分かります。

!FORMULA[225][1119143684][0] の大小関係 $\sin$ の大小関係

また、操作を繰り返したときに「周期的に同じ形になる」ための必要十分条件は、「特定の周波数以外の振幅が $0$ であること」であることも少し考えればわかります。

位相の変化を調べる

次に、位相についても調べたいと思います。
そのために、もう一度、 $g_{k} (n)$ と $g_{s k} (n)$ の式の比較をみてみましょう。

$g_{k} (n) = \frac{1}{N} \sum_{j = 0}^{N - 1} y_{j} \cos \frac{2 k π (n - j)}{N}$

$k \neq 0$ のとき、位相を $(\frac{k π}{N} + \frac{π}{2})$ ずらしたものになっていますので、写像を $4$ 回繰り返すと位相は $(\frac{4 k π}{N} + 2 π)$ ずれて、元の正 $\frac{N}{M}$ 角形と同じ形に戻ることがわかります。

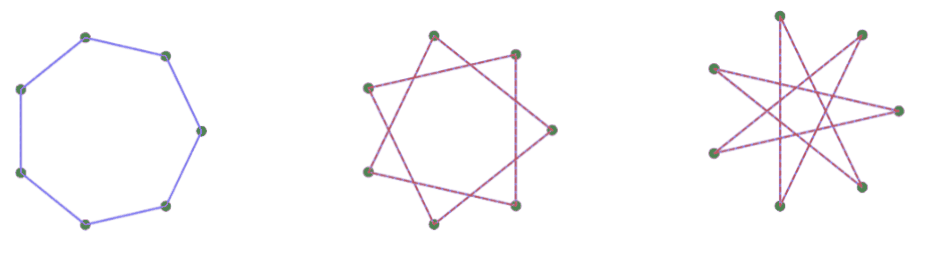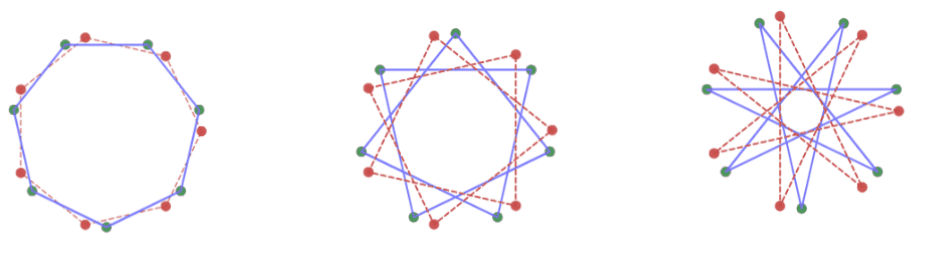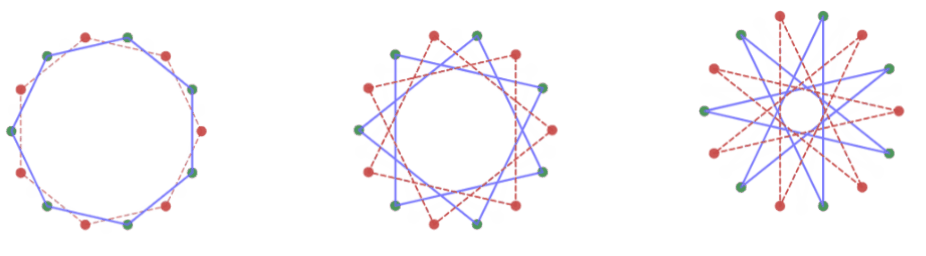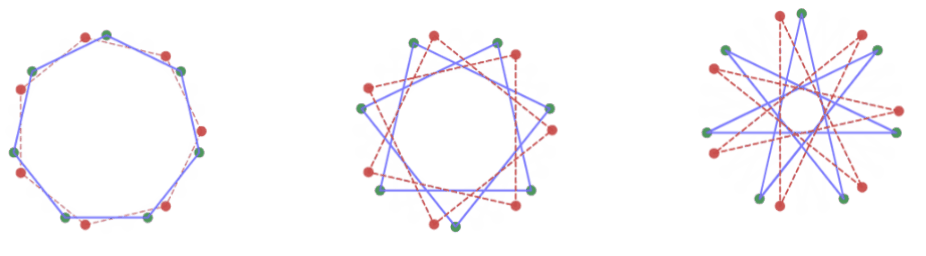位相は周期4でループする

結論

これで、先の予想はすべて離散フーリエ変換で説明できることがわかりましたね!

元の形と収束先の形についての法則

・正 $\frac{N}{M}$ 角形　→　正 $\frac{N}{M}$ 角形　(周期 $4$ でループ)

・正 $\frac{N}{M}$ 角形をアフィン変換した形　→　正 $\frac{N}{M}$ 角形をアフィン変換した形　(周期 $4$ でループ)

・どちらでもない偶数角形　→　 $2$ 点に収束

・どちらでもない奇数角形　→　最も鋭角な正 $\frac{N}{M}$ 角形をアフィン変換した形に収束

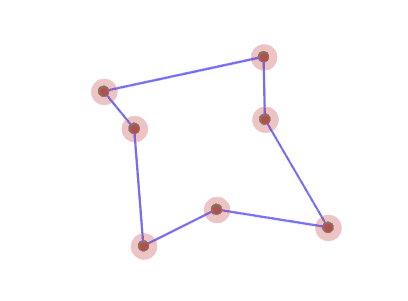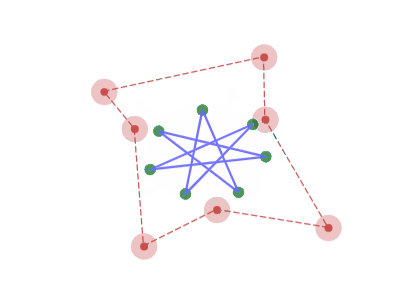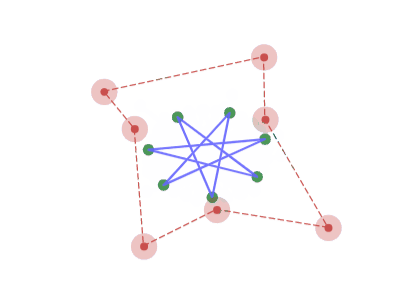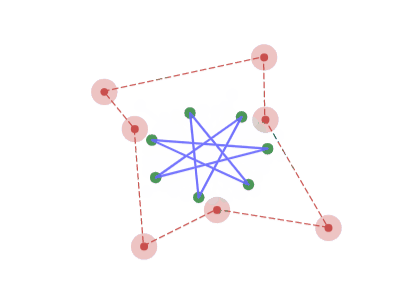周波数の高い成分が残る

もう少し詳しくまとめてみます。

$g_{k} (n) = \frac{1}{N} \sum_{j = 0}^{N - 1} y_{j} \cos \frac{2 k π (n - j)}{N}$

$N$ 角形に今回の写像を繰り返したとき、頂点の $x$ 座標又は $y$ 座標を周波数 $1$ ～ $⌊ \frac{N}{2} ⌋$ のサインカーブの成分に分解すると、周波数の低い成分の振幅は高い成分の振幅と比べて等比級数的に小さくなっていくため、最終的にもとの配置で最も周波数の高い成分のみの図形へと収束していきます。
また、収束先の図形は写像を $2$ 回繰り返すと逆向きになり、 $4$ 回繰り返すと元に戻ります。

おわりに

多角形の写像を分析するのに、離散フーリエ変換を驚くほどうまく利用することができました。
正直なところ、これほどうまくいくとは思ってもいませんでしたので、とても気持ちよかったです。

面白い問題を考えていただいた盛田みずすましさんに感謝してこの記事をささげたいと思います。

分析に使ったDesmosへのリンクを貼っておきますので、良かったら遊んでみてください。

Desmos:離散フーリエ変換 xyと頂点の置換2

また、今回の問題と類似する現象で、「任意の多角形の中点をつないで新しい多角形を作る写像を繰り返すと、楕円状の配置へ収束していく」という現象があります。

この記事の方法を応用すれば、この現象も離散フーリエ変換で説明できることがわかりますので、良かったら考えてみてくださいね。

参考文献

[1]

鏡慎吾, やる夫で学ぶディジタル信号処理, 閲覧日 2021年11月8日, http://www.ic.is.tohoku.ac.jp/~swk/lecture/yaruodsp/main.html

投稿日：2021年11月8日

この記事を高評価した人

高評価したユーザはいません

この記事に送られたバッジ

バッジはありません。

バッチを贈って投稿者を応援しよう

バッチを贈ると投稿者に現金やAmazonのギフトカードが還元されます。

投稿者

apu_yokai

488

66813

他の人のコメント

コメントはありません。

読み込み中

apu_yokai

離散フーリエ変換で多角形の写像を分析する(GIF有)

はじめに
きっかけのツイート
実際にやってみる
$3$ 角形の場合
正 $\frac{N}{M}$ 角形の場合
正 $\frac{N}{M}$ 角形をアフィン変換した形の場合
対称性のない配置の場合はどうなる?
離散フーリエ変換で周期的な数列の一般項をサインカーブの和で表現する
頂点の座標を通過する関数を構成する
サインカーブの和を構成する
検算
$g_{k} (n)$ がサインカーブを描くことを確認する
対称性を使って必要な式の数を減らす
視覚化
$N$ 角形の $y$ 座標(又は $x$ 座標)は、 $⌊ \frac{N}{2} ⌋$ 個のサインカーブの和で表すことができる
$N$ 角形の $y$ 座標(又は $x$ 座標)は、正 $\frac{N}{M}$ 角形上を移動する点の座標の和で表すこともできる
多角形の頂点の位置ベクトルを移す写像
位置ベクトルを変換したあとの周波数ごとの振幅・位相の変化を調べる
振幅の変化を調べる
一般の $N$ 角形の場合
位相の変化を調べる
結論
おわりに
参考文献

離散フーリエ変換で多角形の写像を分析する(GIF有)

はじめに

星型正多角形の表記について

きっかけのツイート

実際にやってみる

3 角形の場合

正 NM 角形の場合

正 NM 角形をアフィン変換した形の場合

位置ベクトルの差で考える

アフィン変換しても写像パターンは変わらない

対称性のない配置の場合はどうなる?

離散フーリエ変換で周期的な数列の一般項をサインカーブの和で表現する

頂点の座標を通過する関数を構成する

サインカーブの和を構成する

検算

gk(n) がサインカーブを描くことを確認する

対称性を使って必要な式の数を減らす

視覚化

N 角形の y 座標(又は x 座標)は、⌊N2⌋ 個のサインカーブの和で表すことができる

N 角形の y 座標(又は x 座標)は、正 NM 角形上を移動する点の座標の和で表すこともできる

多角形の頂点の位置ベクトルを移す写像

k=0 のとき

k≠0 のとき

位置ベクトルを変換したあとの周波数ごとの振幅・位相の変化を調べる

振幅の変化を調べる

写像を繰り返し適用したあとの収束先

例外について

一般の N 角形の場合

位相の変化を調べる

結論

おわりに

参考文献

この記事を高評価した人

この記事に送られたバッジ

投稿者

コメント

他の人のコメント

$3$ 角形の場合

正 $\frac{N}{M}$ 角形の場合

正 $\frac{N}{M}$ 角形をアフィン変換した形の場合

$g_{k} (n)$ がサインカーブを描くことを確認する

$N$ 角形の $y$ 座標(又は $x$ 座標)は、 $⌊ \frac{N}{2} ⌋$ 個のサインカーブの和で表すことができる

$N$ 角形の $y$ 座標(又は $x$ 座標)は、正 $\frac{N}{M}$ 角形上を移動する点の座標の和で表すこともできる

$k = 0$ のとき

$k \neq 0$ のとき

一般の $N$ 角形の場合