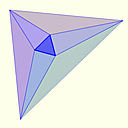
つくってあそぼ / 非デザルグ幾何
本記事は Mathlog Advent Calender 2021 の22日目として書かれています.
デザルグの定理が成立しない平面射影幾何の構成を具体的な目標としながら,平面射影幾何におけるデザルグの定理と体構造との対応を概観します.
注) ここでいう「つくってあそぼ」とは,「作ったもので遊ぼう」ではなく「作ることを遊ぼう」の意です.
デザルグの定理
まず,通常の平面幾何におけるデザルグの定理とは何かを述べます.
$2$つの三角形$ABC,A'B'C'$において,
$3$つの直線$AA',BB',CC'$が共点でありかつ
$AB$と$A'B'$,$BC$と$B'C'$,$CA$と$C'A'$のうちどの組も平行でないならば,$3$つの交点$AB\cap A'B',BC\cap B'C',CA\cap C'A'$は共線である.
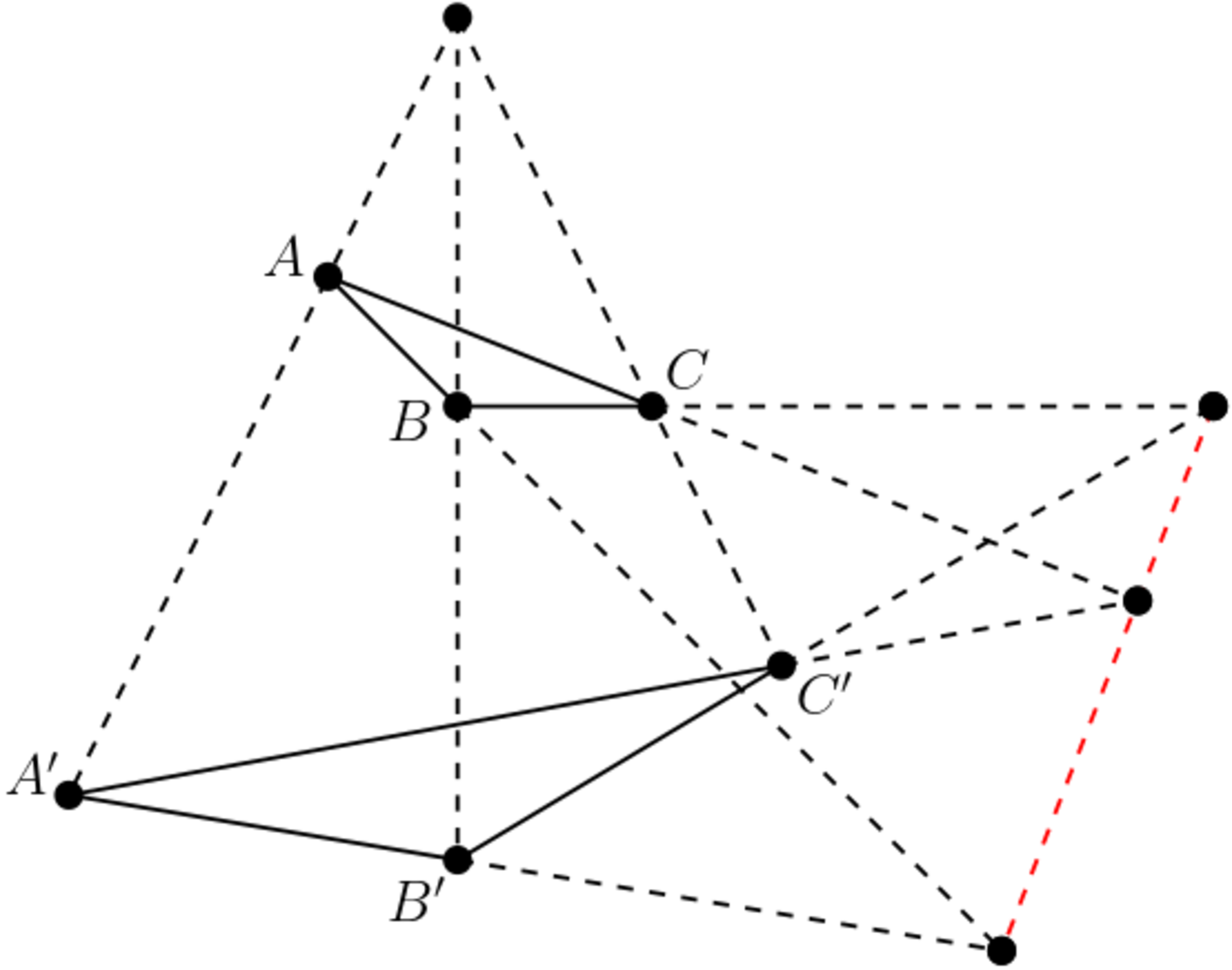
注) 一点で交わることを共点であるといい,一直線上にあることを共線であるといいます.
これはメネラウスの定理を用いて初等的に示せます.しかしながら,$AB$と$A'B'$,$BC$と$B'C'$,$CA$と$C'A'$の中で仮に平行な組があったとしても以下に述べる亜種のように"似た"主張は成り立ちますから,「どの組も平行でない」という但し書きによって場合分けが生じるのは無粋に感じられます.
$2$つの三角形$ABC,A'B'C'$において,
$3$つの直線$AA',BB',CC'$が共点でありかつ$AB$と$A'B'$が平行ならば,$2$つの交点$BC\cap B'C',CA\cap C'A'$を通る直線もそれらに平行である.

$2$つの三角形$ABC,A'B'C'$において,
$3$つの直線$AA',BB',CC'$が共点でありかつ$AB$と$A'B'$が平行かつ$BC$と$B'C'$が平行ならば,$CA$と$C'A'$も平行である.

またこのことから,デザルグの定理はユークリッド幾何に居ては窮屈な定理なのではないかとも思えます.
そこで,これらを統一的に解釈するにはどうしたらよいでしょうか.結論を言ってしまえば,次の条件($\star$)を満たすように,ユークリッド平面に新たな点を付け加えるのです.
条件($\star$) 任意の$2$直線はちょうど$1$点で交わる.
すると,ユークリッド平面上での平行線も交点をもつようになりますから,2つの亜種についても最初の書き方が意味をもつ,すなわち同様の定理だったことがわかります.さらには$AA',BB',CC'$の中に平行なものがあってもデザルグの定理の主張がそのまま適用できます.

こうして点を付け加えた結果できたものを実射影平面といいます.詳しくは次節で述べますが,デザルグの定理は射影平面での定理と見なすのが自然であるということです.
実射影平面
では条件($\star$)を満たすためにどのような点を付け加えるべきか考えましょう.
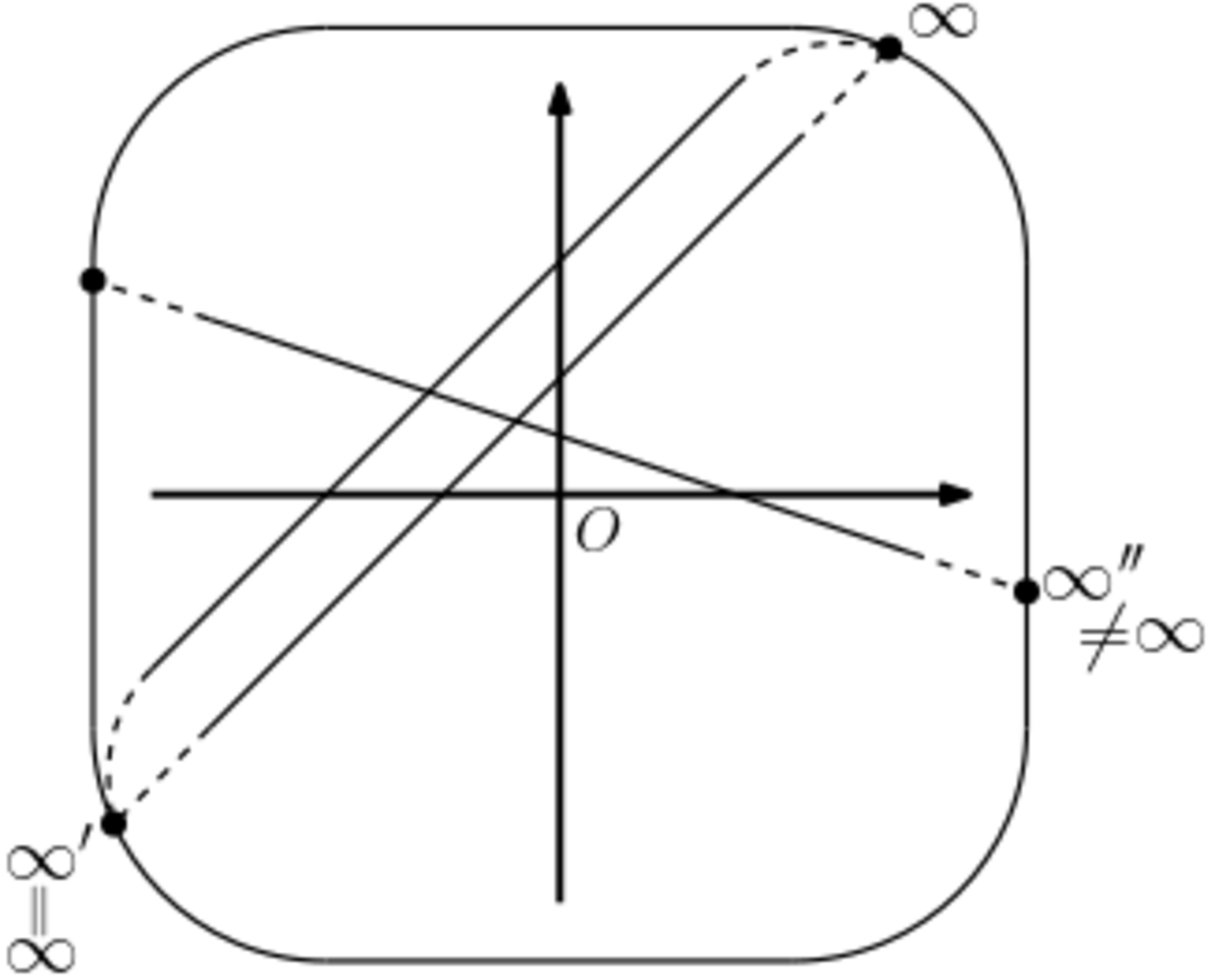
はじめに,ユークリッド幾何では交わっていなかった$2$つの平行線にちょうど$1$つの交点を設定します.無限の彼方で交わるイメージなので,この点を無限遠点といいます.このとき,実射影平面における直線はユークリッド平面における直線にそれぞれ対応する無限遠点$1$つを付け加えたものとなります.前節の通り,任意の$2$直線がちょうど$1$点で交わるようにしたいので,直線の無限の彼方は両側とも同じ無限遠点です.また,平行でない直線には違う無限遠点を割り振る必要もあります.
さらに,亜種その2を説明できるようにするため,無限遠点たちを集めてできる直線も考えます.これを無限遠直線といいます.よって実射影平面の点の集合はユークリッド平面に"ふち"として無限遠直線を足したものだということです.
ちなみに,"極限"(ここでは無限遠)を持つように補う操作を完備化といい,幅広いシーンで現れます.
図形的に考察してきましたが,代数的取り扱いがしやすい形で実射影平面を構成してみると次のようになります.
$3$つの実数からなる連比の集合
$$\lbrace [x:y:z]\ |\ xyz \neq 0\rbrace$$
を$P^2( \mathbb{R})$とかいて実射影平面という.
ただし,実射影平面の点の区別は連比の区別と一致させる.例えば
$[1:-2:3]=[-2:4:-6]\neq [-2:4:0]$
などとなる.
このような連比による点の表示を斉次座標といいます.
先ほどの説明と見比べると,ユークリッド平面上の点$(x,y)$は$[x:y:1]$に対応し,原点とそれ以外の点$(x,y)$を通る直線に付け加える無限遠点は$[x:y:0]$に対応します.したがって無限遠直線は$\lbrace [x:y:z]\ |\ xy \neq 0,\ z=0\rbrace$となります.
ところで,実射影平面は"工作"ができます.ゴロリ「ほんとかなあ」
材料は長方形と円板の形をした紙をそれぞれお手元にご用意ください.まずは長方形の紙を一回ねじってから両端を貼り合わせます.これはいわゆるメビウスの帯になっていますね.次に円板とメビウス帯のふち同士をくっつけて出来上がりです.ゴロリ「なにこれ?」
…実はクシャクシャに折れたり破れたりすることなく作ることは$3$次元ではできません.$4$次元ユークリッド空間なら可能ですのでもし行く機会があればやってみてください.以上,申し訳程度の「つくってあそぼ」要素でした.
平面射影幾何の公理
より広く,次の公理系で定められた幾何を平面射影幾何といいます.
(実射影平面が平面射影幾何をなすモデルであることは確かめてみてください.)
点の集合$\mathcal{P}$と直線の集合$\mathcal{L}$の組$(\mathcal{P},\mathcal{L})$が次を満たすとき平面射影幾何をなすという.
- 異なる$2$点を通る直線がただ一つ存在する.
- 異なる$2$つの直線は必ず交わる.
- 共線でない$3$点が存在する.
- 直線は少なくとも$3$点以上を含む.
注) 実射影平面の場合から円滑に話を展開するために"点"や"直線"と呼んでいますが,これらが実際の点や直線である必要はありません.集合の組$(\mathcal{P},\mathcal{L})$が上記の公理系を満たすならば$\mathcal{P}$の元を点,$\mathcal{L}$の元を直線と「呼ぶことにする」というのが公理に対する姿勢です.射影幾何の公理化をはじめに考えたのはドイツのウィーナー(ウィーナー過程のそれとは別人)で,ヒルベルトによって大きく華開く公理主義の出発点となりました.
これはユークリッドが原論で著した点と直線の配置に関わる平面幾何の公理系のうち平行線公準を条件($\star$)に変更したものです.点と直線のみで定まることから定規の幾何学と呼ばれることがあります.
ここで射影幾何の歴史を軽く追っておきます.射影的性質の研究は古代ギリシアのアポロニウスやエジプトのパップスによる円錐曲線論に端を発しています.ただしこのときはまだ円錐面の切断として考えられており,しばらくしてルネサンスを経たフランスのデザルグやその弟子パスカルにより射影が前面に出てきました.そのアイデアを引き継いだモンジュは平行線の交わる世界が図面上の透視図法(遠近法)で表現できることから,画法幾何学の中で射影と切断という考えを用いた射影幾何の原形を整備しました.
理論がまとめ上げられたのは19世紀のことで,その最大の功労者はモンジュの弟子であったポンスレです.彼が射影幾何の研究を集中的に進めたのはなんとナポレオンの遠征に従軍し負傷してロシアの捕虜となっていた2年間だったそうです.
話を元に戻しましょう.射影幾何の重要かつ興味深い性質としてそのポンスレの名を冠する双対原理があります.
点の集合を$\mathcal{P}$,直線の集合を$\mathcal{L}$とした組$(\mathcal{P},\mathcal{L})$が平面射影幾何の公理を満たすならば,組$(\mathcal{L},\mathcal{P})$も平面射影幾何をなす.
実射影平面における直線の集合を次のように捉えると直線と点の等価性がわかりやすくなります.
直線の集合を$\lbrace [a:b:c]\ |\ abc \neq 0\rbrace$とする.ただし,点$[x:y:z]$が直線$[a:b:c]$を通るとは
$$ax+by+cz=0$$となることとする.
よって,平面射影幾何の公理系のみから導かれる全ての定理は主張において点と直線を入れ替えても成立します.
ここからが肝ですが,以上の平面射影幾何の公理からはデザルグの定理は導けないことが知られています.すなわち,デザルグの定理が成り立たない平面射影幾何,非デザルグ幾何が存在するのです.
非デザルグ幾何の構成 / モールトン平面
非デザルグ幾何には点の集合が有限であるものなどいくつかバリエーションがありますが,ここでは実射影平面を少し"歪めて"できるモールトン平面を挙げます.
$\mathbb{R}^2$を点の集合,$(\mathbb{R}\cup \lbrace \infty \rbrace)\times \mathbb{R}$を直線の集合とする.ただし,$(a,b)\in (\mathbb{R}\cup \lbrace \infty \rbrace)\times \mathbb{R}$に対応する$\mathbb{R}^2$内の直線は以下の通りとする.
- $a=\infty$のとき
$x=b$ - $a \geq 0$のとき
$y=ax+b$ - $a \leq 0$のとき
$y= \begin{eqnarray} \left\{ \begin{array}{l} ax+b \ (x \geq 0) \\ \frac{1}{2}ax+b\ (x \leq 0) \end{array} \right. \end{eqnarray}$
実射影平面の構成と同様,これに無限遠直線を加える完備化で得られる空間をモールトン平面という.
負の傾きをもつときは$y$軸を境に屈折するような折れ線を直線と定めるわけです.点の集合は実射影平面と変わりありません.
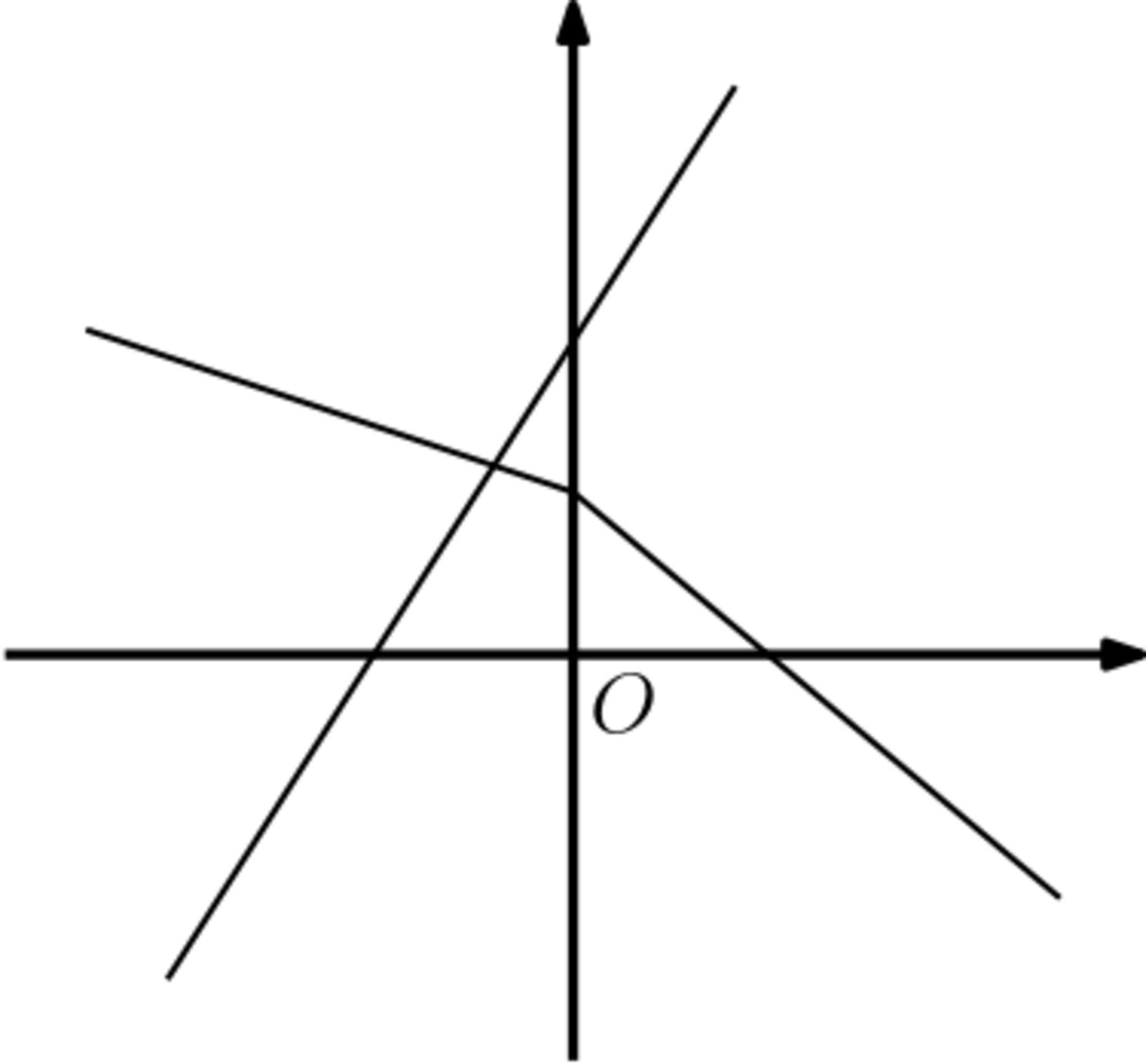
モールトン平面は平面射影幾何をなす.
証明は公理を逐一確認すれば容易にできますが,直線の集合が巧妙に作られた不思議な空間であることがわかりますね.
モールトン平面においてデザルグの定理は成立しない.
以下の状況が反例となる.$\blacksquare$

[発展]デザルグの定理と体構造
本節では体の定義は知っているものとして,もう少し踏み込んだ話をします.
平面射影幾何のうちかなり大きなクラスとして,体$K$から定まる射影平面$P^2(K)$があります.
$K^3\setminus \lbrace 0 \rbrace$上の同値関係$\sim$
$$x\sim y \ \Longleftrightarrow \ \exists k \in K \quad x=ky$$
により射影平面$P^2(K)$を
$$P^2(K)=(K^3\setminus\lbrace 0\rbrace)/\sim$$
と定義する.
これは$K$上の$1$次元線型空間全体の集合とも言えます.
実は射影平面であること,すなわちある体$K$を用いて$P^2(K)$と表されることと,デザルグの定理まで公理に含めた平面射影幾何をなすことは同値です.次の対応が知られています.
デザルグの定理を満たす平面射影幾何と体の間には$1$対$1$対応がある.
体構造との対応については,次のパップスの定理も重要です.
$3$点$A,B,C$が共線でありかつ$3$点$A',B',C'$が共線であるならば,
$3$交点$AB'\cap A'B,BC'\cap B'C,CA'\cap C'A$は共線である.

平面射影幾何がパップスの定理を満たすことと,ある可換体$K$を用いて$P^2(K)$と表されることは同値となります.よって,ある平面射影幾何がパップスの定理を満たすならばデザルグの定理を満たします.特に有限個の点からなる射影幾何においてはウェダーバーンの小定理により逆も成立します.
このようにデザルグの定理は結合性を,パップスの定理は可換性を主張するものです.幾何学と代数学の連携が実に鮮やかですね.
なお,点と直線に加えて平面も定義できる「$3$次元以上」の射影幾何ではデザルグの定理を常に満たすことが知られています.平面外の点を取れることが効いており,次元を一つあげて考える直感的な証明は面白くて有名です.冒頭のデザルグの定理の図を立体視すると,三角形$ABC,A'B'C'$をそれぞれ含む平面の交線上に各交点が並ぶ様子がわかります. メネラウスの定理再考 は大いに参考になるでしょう.デザルグの定理の双対は元の命題の逆になっていますから,双対原理により逆も自動的に成立します.この同値な条件を満たす$2$つの三角形$ABC$と$A'B'C'$は配景的であるといいます.
注) 非デザルグ幾何には八元数を介して例外型リー代数との関連もあります.
現代幾何学の根っことしての射影幾何
純粋数学を学ぶ方であれば誰しも位相空間や可微分多様体の基本的な例として必ず射影空間に触れることになるでしょう.豊富な構成方法があり,これは捉えられる側面が多種多様であることを意味しています.
例えば,原点を通る直線のモジュライ空間としての見方は強く興味を惹きます.実際,ユークリッド空間内の原点を通る直線はその方向ベクトルから実射影平面の点との対応を定められます(直線のコレクターになって実射影平面に収蔵している気分?).
また,射影幾何といえばエルランゲン・プログラムは外せません.これは1872年にクラインが23歳でエルランゲン大学の教授となったとき示した指針です.変換群の概念を通して幾何学を統一的に解釈する試みでした.
群$G$とそれが(推移的に)作用する幾何学的構造をもった集合$X$との組$(G,X)$こそが幾何であり,図形すなわち$X$の部分集合の性質で$G$による作用のもと不変な性質を調べることが幾何学の目的である.
このプログラムにおいて角度や長さを考えない射影幾何(射影空間と射影変換群の組)は始祖の位置付けとなります.すなわち,ユークリッド幾何,球面幾何,双曲幾何といった古典幾何はどれも射影幾何の制限から得られる部分幾何となります.射影幾何の最重要の不変量は複比です.
一方でリーマン幾何はエルランゲン・プログラムには組み込めませんでしたが,カルタンにより接続という概念が登場したことで不変性に着目した研究はその後も発展し続けることになるのです.また,まだ歴史の浅い位相幾何学はクラインの哲学をより色濃く反映した分野と言えるでしょう.