文献あり

サッカーリーグの勝ち点問題

2455

こんにちは！ヘカテーと申します！院生をやっていました！
今回の記事は日曜数学アドベントカレンダー 23日目の記事です！

私が大学2年生の時に取っていた哲学の授業後に、
諸君らは数学科だから是非教えて欲しい、ということでサッカーが好きな教授から出された
サッカーリーグの勝ち点問題について紹介します。
（本来であればこの問題の検算にバーンサイドの補題を使いたかった（当時使っていた）のですが直前で計算が合わなくなってしまったので消しました。泣く。）→計算が合ったので今月中には追記したい(2/9)

サッカーの風景

サッカーリーグの勝ち点問題

皆さんはサッカーのリーグ戦（総当たり戦）の評価方法をご存じでしょうか？
現在の方式では勝利へのインセンティブを高め、攻撃力の向上をねらうことを目的として勝ったときの点数により比重がかけられた評価方法になっているそうです。
そこで以下の問題です。

サッカーのリーグ戦における勝ち点は何通りあるか？

A, B, C, Dの4チームでリーグ戦をする。それぞれの試合の勝敗の結果に応じて、各チームに勝ち点という点数をつける。
サッカーにおける一試合の勝ち点は、勝ったら+3点、引き分けたら+1点、負けたら+0点である。
すべての試合が終了したとき、勝ち点の結果は何通りあるだろうか？
ただし、勝ち点の組み合わせを考える際、各チームに区別をつけないものとする。

4チームの総当たりなので計${}_4 \mathrm{C}_2=6$ 試合あり、単純な試合の結果は$3^6=729$通りあります。
このうち、各チームに区別をつけないで、勝ち点の結果だけを考えると何通りになりますかという問題です。

例えば、6試合の結果が以下の場合、

A VS B　$\rightarrow$ 引き分け
A VS C　$\rightarrow$ 引き分け
A VS D　$\rightarrow$ Aの勝ち、Dの負け
B VS C　$\rightarrow$ 引き分け
B VS D　$\rightarrow$ 引き分け
C VS D　$\rightarrow$ 引き分け

Aは1勝2分け、Bは3分け、Cは3分け、Dは1敗2分けとなる為、
それぞれの勝ち点は、Aが5点、Bが3点、Cが3点、Dが2点という結果になります。

しかしここで、
A VS D　$\rightarrow$ Dの勝ち、Aの負け　だったとしても
Aが2点、Bが3点、Cが3点、Dが5点という結果となり、
勝ち点の組み合わせとしては同じになるので、区別されません。
（1勝2分けが一人、3分けが二人、1敗2分けが一人という結果に変わりはない。）

ちなみに、これと同じ問題が2019年度慶應義塾中等部の入学試験問題算数大問7(2)に出題されています。
(全20問を40～45分で解くという状況下で、果たしてこの問題を解き切った小学生は存在するのでしょうか…)
$$ $$

この問題に対して当時の私は、まず4チームの対戦表を書いて〇☓△と結果を書き込んで数えてみて様子を…とやってみたのですが
この方法だと…
$$ $$
${\LARGE 試合の様子が全く想像出来ない！！！！}$

ことに気付きました。

どうせ数えるなら6試合の様子が一目で分かるように書きたいということで、グラフを使って視覚的に数えることにしました。

そこで、そのグラフの表し方も兼ねて、まずは小さな例として3チームの場合を見ていきます。
3チーム総当たりなので，試合数は3試合で、勝敗のパターンは$3^3=27$通りあります。

サッカーのリーグ戦における勝ち点は何通りあるか？（3チーム版）

3チームの総当たり戦における試合（勝ち点）の結果は以下の7通りである。
（一試合の勝ち点は、勝ったら+3点、引き分けたら+1点、負けたら+0点）
上から、一度も勝敗がつかなかった場合（全引き分け）、一度だけ勝敗がついた場合、2試合は勝敗がついた場合、3試合とも勝敗がついた場合に分けられている。
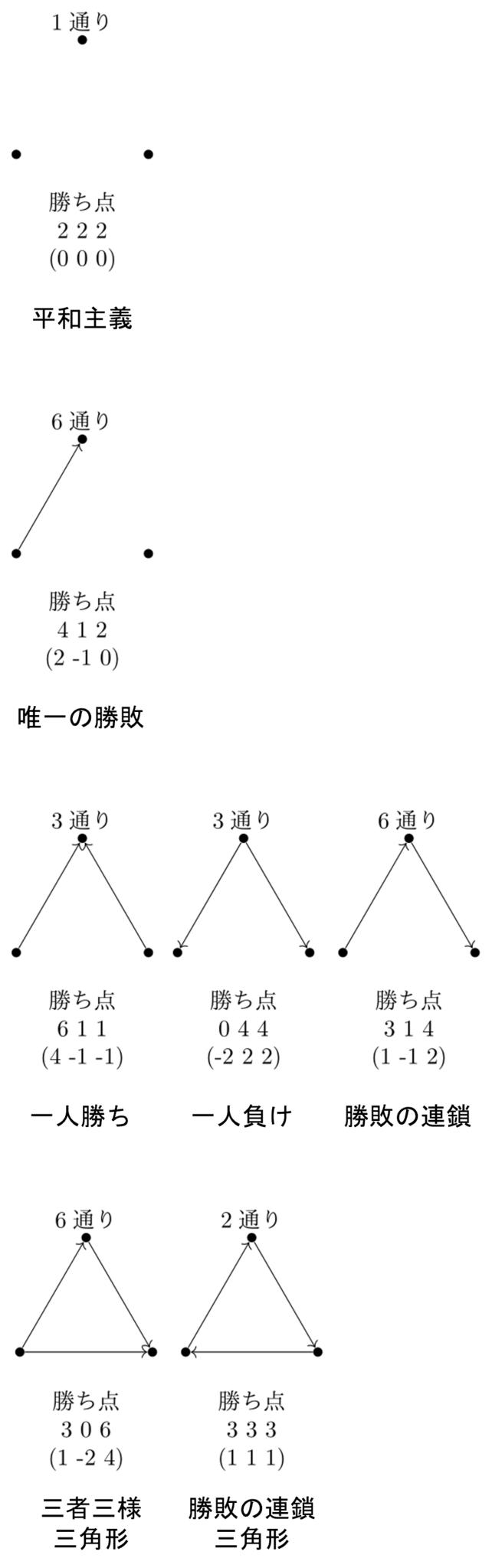勝敗がついた試合数でまとめた3チーム総当たり戦の試合結果一覧

グラフの見方

グラフは、矢印の先（終点）が勝ったチームを表し、矢印の元（始点）が負けたチームを表す。引き分けの場合は、矢印（有向辺）も無向辺も引かない。
（要するに自己ループと多重辺を許さない有向グラフ（簡単にグラフと呼ぶ）で試合の結果を表す。）
今回は左の図で3試合の総当たり戦がすべて引き分けであることを表す。（特に左の図は総試合数が0の状態ではないことに注意。）

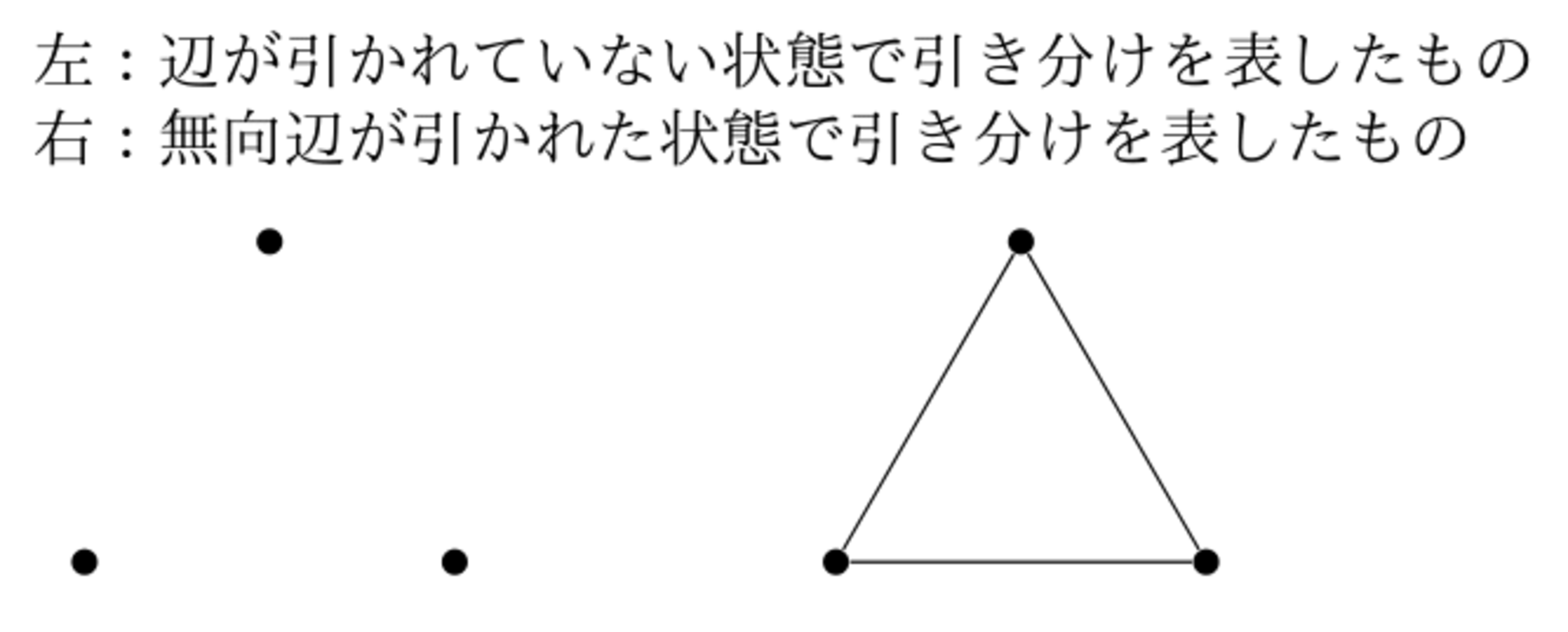引き分けの表し方に注意

グラフの上部には勝ち点が同じで、グラフ（誰が勝ち、誰が負けたか）が異なるものが何通りあるかが書いてある。
グラフの下部には3チームそれぞれの勝ち点が書かれているが、（）内には、問題の定式化の為、勝ち点を勝ったら2点、負けたら-1点、引き分けたら0点とした場合の勝ち点が書かれている。
グラフの下部には~~特に規則もなく~~個人的にグラフを命名した名前が載っている。

勝敗がついた試合数ごとの勝ち点のパターン数の合計で計7通り、各グラフ上部に書かれた、勝ち点は同じでグラフ（勝敗の付き方）が異なるものの合計で計27通りになります。

27通りあったものが勝ち点の組み合わせだけ見ると7通りになるわけですね！

当時の私は、この3チームの場合と同様に、4チームの場合もグラフを1つずつ書いていきました。

その結果がこちらです。（長いので適宜しまってあります。図が小さいかもしれない。）
グラフ下部に特徴が分かるように筆者の個人的な命名（共通する辺を持たないように一筆書きを何回したらグラフが書けるか）を載せてみました。特に数学的背景がある命名ではないですが、グラフが対になっている感（双対感）が分かる気がします。）

勝敗がついた試合数が0コ～2コの場合（計1+1+4=6通り）

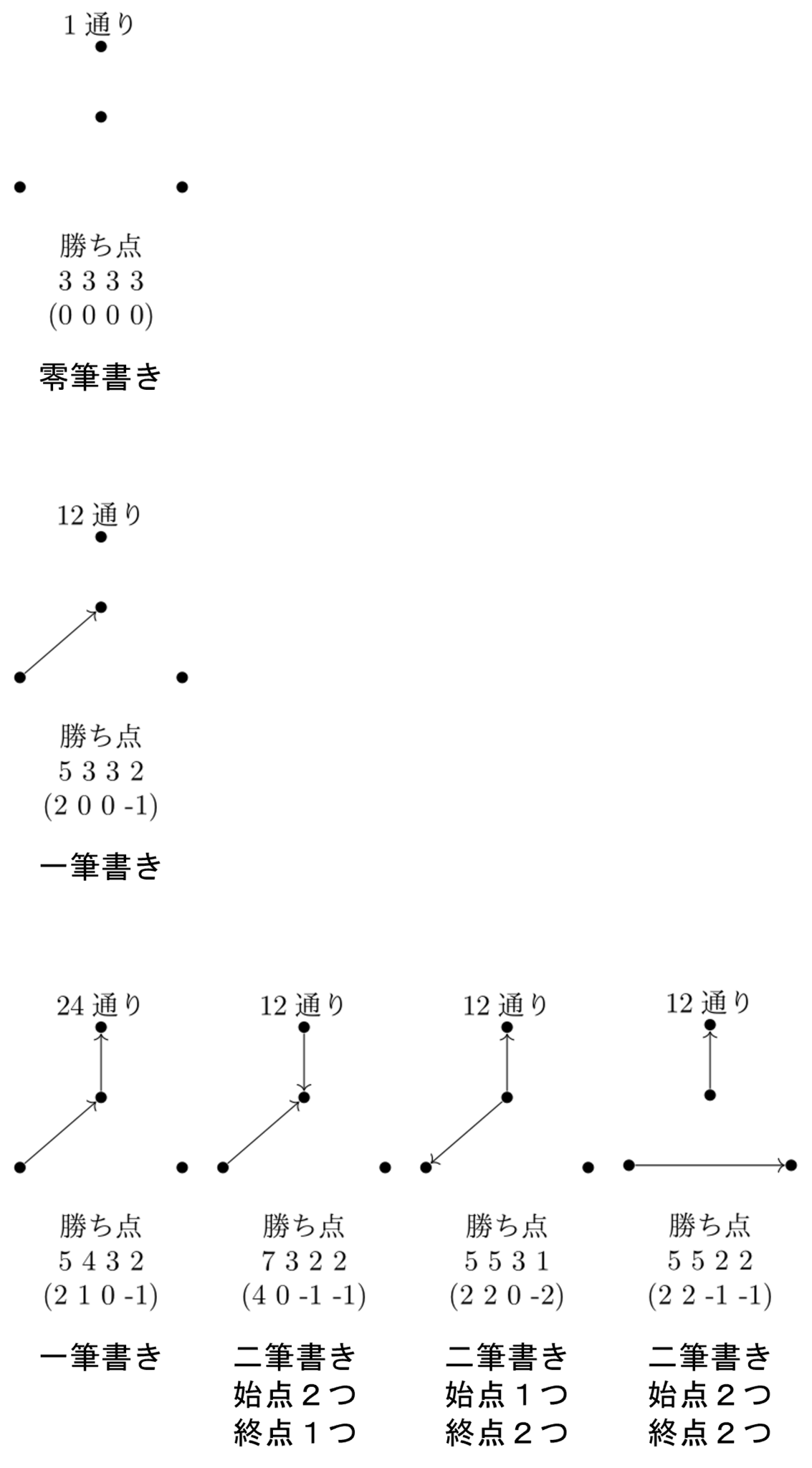勝敗がついた試合数が0コ～2コまでの試合結果

勝敗がついた試合数が3コの場合（計10通り）

勝敗がついた試合数が3コの試合結果

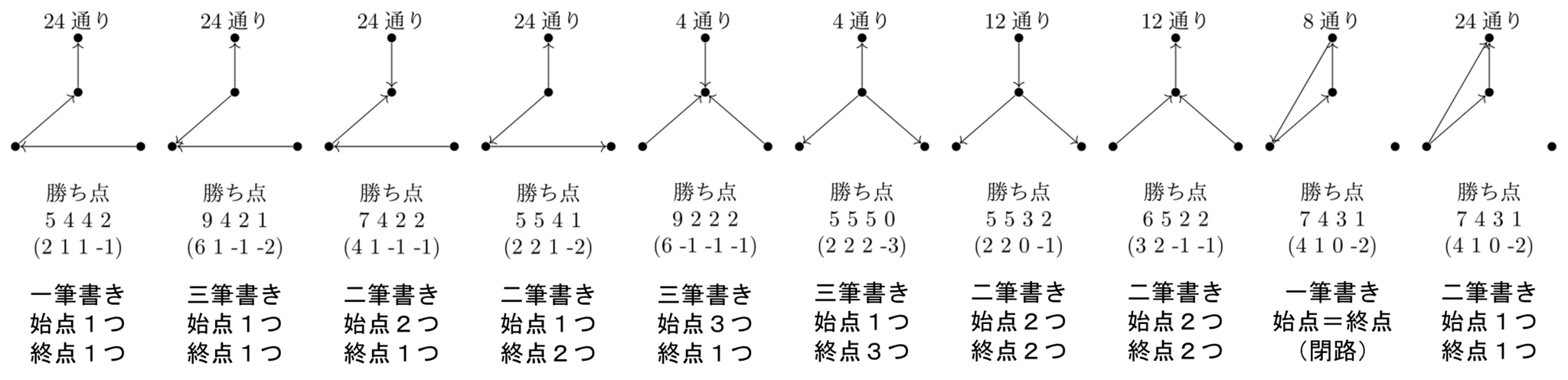
勝敗がついた試合数が4コの場合（計11通り、（グラフとしては計12通り））

勝敗がついた試合数が4コの試合結果

勝敗がついた試合数が5コの場合（計9通り、（グラフとしては計10通り））

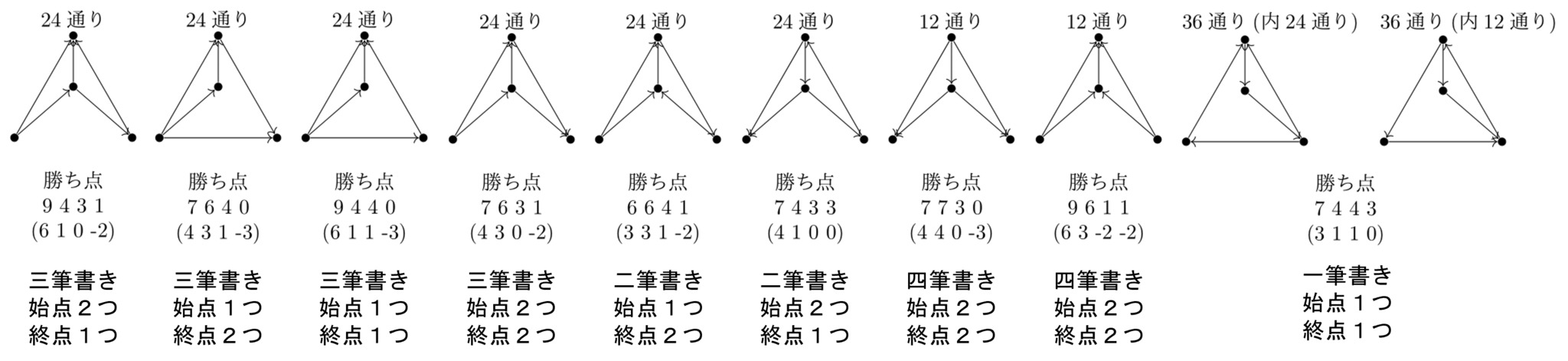勝敗がついた試合数が5コの試合結果

勝敗がついた試合数が6コの場合（計4通り）

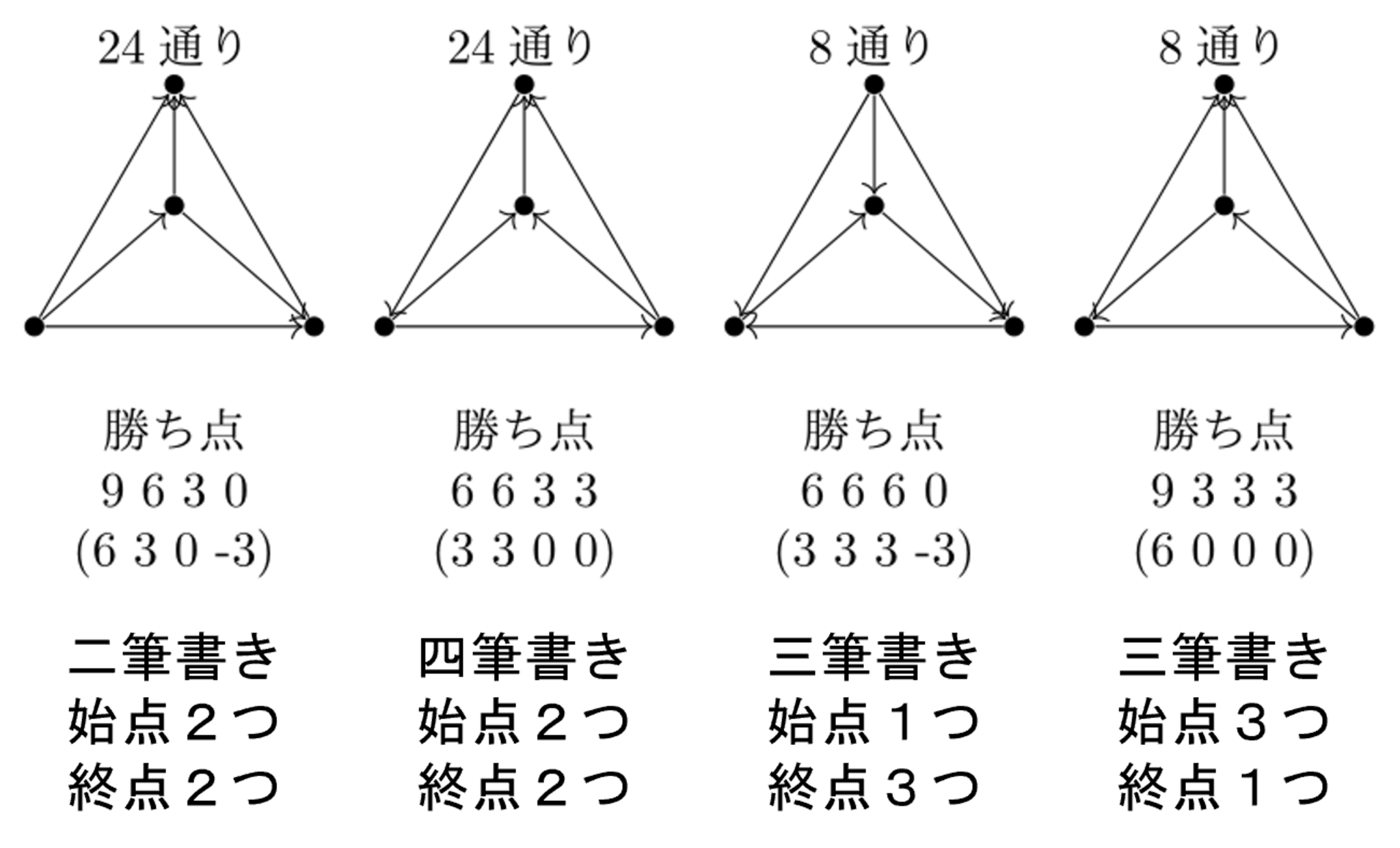勝敗がついた試合数が6コの試合結果

この結果の面白い点としては
グラフとしては合計42通りあって、勝ち点の組み合わせパターンとしては合計40通りとなることです。

つまり、勝ち点（頂点の周りの様子）の組み合わせは同じだけど、各頂点をどう入れ替えてもグラフとしてぴったり重なることは出来ないパターンが2通りあるということです。

また、一応重複して数えているもの（ダブり）を考慮するとこれで計729通りになっているのですが、
当時パソコンの力を使いこなせなかった私は、これらの計算にミスが無いか、試合結果を表すグラフにヌケやダブりが無いかとても不安になっていました。

（そこで、活躍したのが次のバーンサイドの補題でしたといって、バーンサイドの補題を使ってこのグラフの総数の42通りを計算で確かめる予定だったのですが‥‥‥計算が直前で合わず。出来次第追記します。)

しかし、今では私もコンピュータの力を借りることが出来る様になりました。
~~何故なら、競プロerの友達が出来たから。~~

以下の~~書いてもらった~~C++のコードで計算結果を確かめることが出来ます。

C++の開発環境が手元に無い方でも是非 ideone 等で動作を確認してみて下さい！

勝ち点の設定とチーム数を自由に変更した上で勝ち点のパターンの総数を出してくれるコード

          #include <set>
    #include <cmath>
    #include <vector>
    #include <algorithm>
    #include <iostream>

    using namespace std;

    int main() {

    int num_team = 4;
    int score_win = 3;
    int score_draw = 1;
    int score_lose = 0;

    set<vector<int> > points;

    long long num_match = num_team * (num_team - 1) / 2;
    vector<vector<int> > result(num_team, vector<int>(num_team));
    for (long long result_ll = 0; result_ll < pow(3, num_match); result_ll++) {
        long long result_tmp = result_ll;
        for (int i = 0; i < num_team; i++) {
            for (int j = i + 1; j < num_team; j++) {
                result[i][j] = result_tmp % 3;
                result[j][i] = 2 - (result_tmp % 3);
                result_tmp /= 3;
            }
        }
        vector<int> points_tmp(num_team);
        for (int i = 0; i < num_team; i++) {
            for (int j = 0; j < num_team; j++) {
                if (i == j) continue;
                switch (result[i][j]) {
                case 0: points_tmp[i] += score_win;  break;
                case 1: points_tmp[i] += score_draw; break;
                case 2: points_tmp[i] += score_lose; break;
                }
            }
        }
        sort(points_tmp.begin(), points_tmp.end());
        points.insert(points_tmp);
    }

    cout << points.size() << endl;
    for (set<vector<int> >::iterator itr = points.begin(); itr != points.end(); ++itr) {
        vector<int> points_tmp = *itr;
        for (int i = 0; i < num_team; i++)
            cout << points_tmp[i] << " ";
        cout << endl;
    }

    return 0;
    }

勝ち点の設定とチーム数を自由に変更した上で勝ち点のパターンの総数を出してくれるコード（4チーム勝ち3点引き分け1点負け0点の結果）

40 0 3 6 9  0 3 7 7  0 4 4 9  0 4 5 7  0 4 6 7  0 5 5 5  0 6 6 6  1 1 6 9  1 1 7 7  1 2 4 9  1 2 5 7  1 2 6 7  1 3 4 7  1 3 4 9  1 3 5 5  1 3 5 7  1 3 6 7  1 4 4 7  1 4 5 5  1 4 5 6  1 4 6 6  2 2 2 9  2 2 3 7  2 2 4 7  2 2 5 5  2 2 5 6  2 3 3 5  2 3 4 5  2 3 4 7  2 3 5 5  2 4 4 5  2 4 4 6  3 3 3 3  3 3 3 9  3 3 4 7  3 3 6 6  3 4 4 4  3 4 4 5  3 4 4 6  4 4 4 4