𝐖𝐙 𝐦𝐞𝐭𝐡𝐨𝐝 覚書

957

$𝙸 𝚗 𝚝 𝚛 𝚘 𝚍 𝚞 𝚌 𝚝 𝚒 𝚘 𝚗$
　 $A l m k v i s t$ , $B o r w e i n$ , $B r a d l e y$ , $G r a n v i l l e$ , $K o e c h e r$ , $L e s h c h i n e r$ , $R i v o a l$ といったひとたちは，ゼータ値に収束するような収束が速い級数を与えています。
例えば， $K o e c h e r^{'} s f o r m u l a$

\begin{array}{r} \sum_{n = 0}^{\infty} x^{2 n} ζ (2 n + 3) = \sum_{n = 1}^{\infty} \frac{(- 1)^{n - 1}}{n^{3} (\binom{2 n}{n})} (\frac{1}{2} + \frac{2}{1 - \frac{x^{2}}{n^{2}}}) \prod_{k = 1}^{n - 1} (1 - \frac{x^{2}}{k^{2}}) \end{array}

や， $Bailey-Borwein-Bladley f o r m u l a$

\begin{array}{r} \sum_{n = 0}^{\infty} x^{2 n} ζ (2 n + 2) = 3 \sum_{n = 1}^{\infty} \frac{1}{(\binom{2 n}{n}) (n^{2} - x^{2})} \prod_{k = 1}^{n - 1} \frac{k^{2} - 4 x^{2}}{k^{2} - x^{2}} \end{array}

というものがあります。
$K h o d a b a k h s h$ と $T a t i a n a H e s s a m i P i l e h r o o d$ は， $W Z m e t h o d$ を用いてこのような等式を証明しました。これらのゼータ値公式の $W Z m e t h o d$ による証明は，どのようにして超幾何級数と関係しているのでしょうか。またこの関連性によってどのように一般化することができるでしょうか。

$𝐓 𝐡 𝐞 𝐖 𝐙 𝐦 𝐞 𝐭 𝐡 𝐨 𝐝$

　次のような，方向性を持つ各格子辺に重みが付いた格子グラフを考えます。

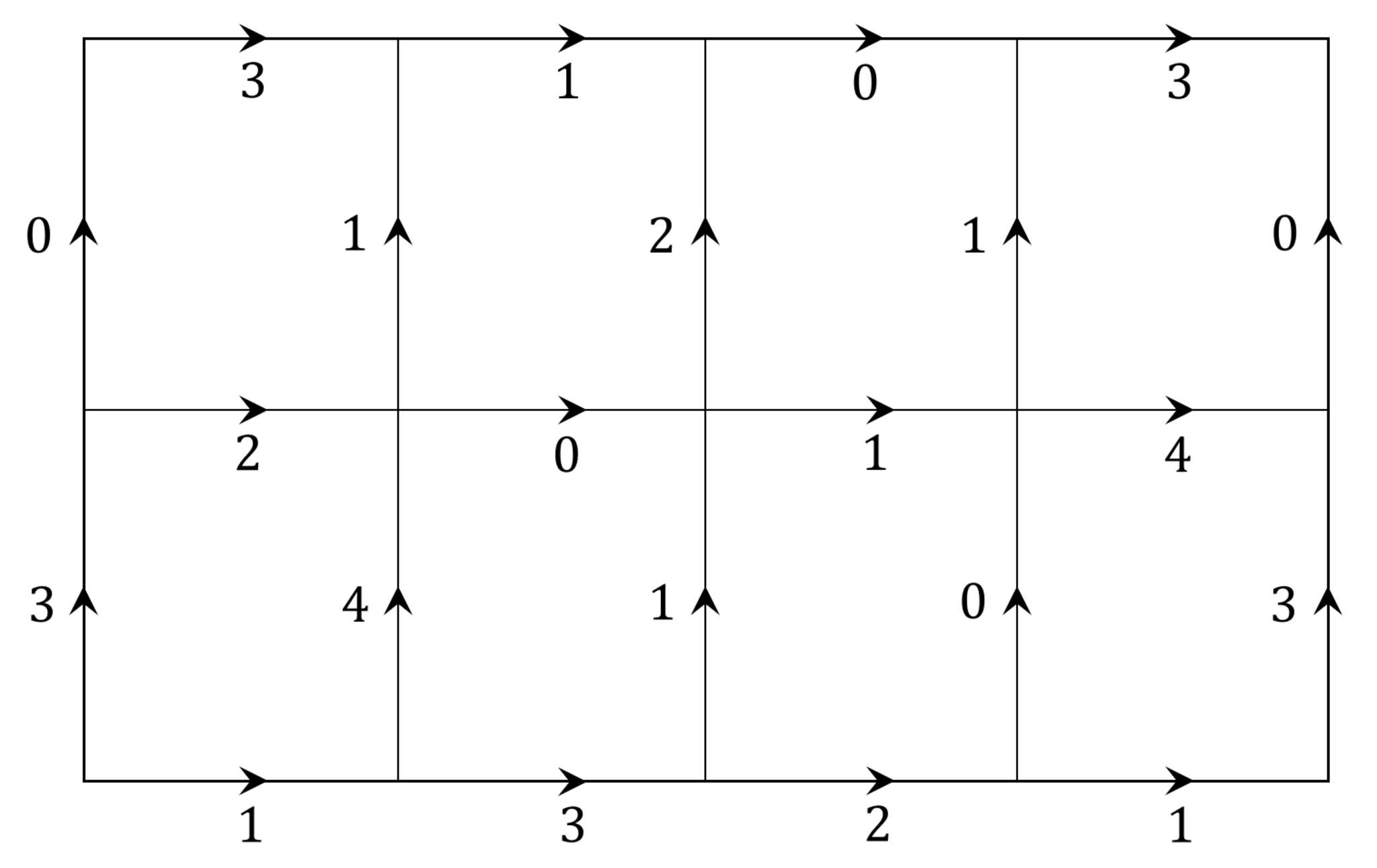
どの二点間においても経路の重みが一致するように設定します(経路不変性)。また，このような性質を持つ格子グラフを $P i G G$ と呼ぶことにします。
$P i G G$ であることを確かめるには，各格子について考えれば十分です。

隣り合わない頂点どうしを新たに結ぶことで，同じ点集合に別の格子を与えることができます。そしてその格子グラフは経路不変性を持ちます。
いま，各頂点が $Z \times Z$ 上にある $P i G G$ があるとします。また， $(i, j)$ から $(i + 1, j)$ までの重みを $F (i, j)$ ， $(i, j)$ から $(i, j + 1)$ までの重みを $G (i, j)$ とします。

経路不変性を式で表せば

\begin{array}{r} F (i, j) + G (i + 1, j) = G (i, j) + F (i, j + 1) \end{array}

となります。この等式を満たす $F, G$ の組を $WZ-pair$ と呼びます。
冒頭の疑問に対して， $F, G$ が特定の形

\begin{array}{r} \frac{Γ (a_{1} i + b_{1} j + v_{1}) \dots Γ (a_{r} i + b_{r} j + v_{r})}{Γ (c_{1} i + d_{1} j + w_{1}) \dots Γ (c_{s} i + d_{s} j + w_{s})} X^{i} Y^{j} \end{array}

を持ってくれるとうれしいです。ここで $a_{n}, b_{n}, c_{n}, d_{n}$ は整数， $v_{n}, w_{n}, X, Y$ は複素数としています。
また，この形で表すことができるということは， $\frac{F (i + 1, j)}{F (i, j)}, \frac{F (i, j + 1)}{F (i, j)}, \frac{F (i, j)}{G (i, j)}$ が有理関数になることを示しています。

この格子グラフですが，格子の頂点の座標は整数でなくても良いことに注意してください。あくまで格子辺の長さが整数であれば格子グラフが形成されるというのが本質です。

$B i n o m i a l t h e o r e m$

　 $F, G$ を次のように定義します。

\begin{aligned} F (i, j) = \frac{Γ (i + j + 2)}{Γ (i + 2) Γ (j + 1)} x^{i} (1 - x)^{j} = (\binom{i + j + 1}{j}) x^{i} (1 - x)^{j} \\ G (i, j) = - \frac{Γ (i + j + 2)}{Γ (i + 1) Γ (j + 2)} x^{i} (1 - x)^{j} = - (\binom{i + j + 1}{i}) x^{i} (1 - x)^{j} \end{aligned}

$F (i, j) + G (i + 1, j) = G (i, j) + F (i, j + 1)$ が成り立つので $(F, G)$ は $WZ-pair$ です。
次の格子を考えます。

経路 $P$ で和をとると

\begin{array}{r} \sum_{i = 0}^{m - 1} F (i, 0) + \sum_{j = 0}^{n - 1} G (m, j) = \frac{1 - x^{m}}{1 - x} - \sum_{j = 0}^{n - 1} (\binom{j + m + 1}{m}) x^{m} (1 - x)^{j} \end{array}

経路 $Q$ で和をとると

\begin{array}{r} \sum_{j = 0}^{n - 1} G (0, j) + \sum_{i = 0}^{m - 1} F (i, n) = - \frac{1 - (1 - x)^{n}}{x} + \sum_{i = 0}^{m - 1} (\binom{i + n + 1}{n}) x^{i} (1 - x)^{n} \end{array}

となります。
よって，

\begin{array}{r} \frac{1 - x^{m}}{1 - x} - \sum_{j = 0}^{n - 1} (\binom{j + m + 1}{m}) x^{m} (1 - x)^{j} = - \frac{1 - (1 - x)^{n}}{x} + \sum_{i = 0}^{m - 1} (\binom{i + n + 1}{n}) x^{i} (1 - x)^{n} \end{array}

という等式を得ます。いま， $m \to \infty$ とすれば

\begin{array}{r} \frac{1 - 0}{1 - x} - 0 = - \frac{1 - (1 - x)^{n}}{x} + \sum_{i = 0}^{\infty} (\binom{i + n + 1}{n}) x^{i} (1 - x)^{n} \end{array}

すなわち

\begin{array}{r} \sum_{i = 0}^{\infty} (\binom{i + n + 1}{n}) x^{i} (1 - x)^{n} = \frac{1}{1 - x} + \frac{1 - (1 - x)^{n}}{x} \end{array}

となります。

$S h a d o w i n g$

　前述の $WZ-pair$ を修飾するにはどうすればよいでしょうか。そこで，次の定理を用います。

$L e m m a .$
　 $(F (i, j), G (i, j))$ が $WZ-pair$ ならば， $F, G$ が収束するような任意の複素数 $α, β$ に対して $(F (i + α, j + β), G (i + α, j + β))$ は $WZ-pair$ である．

これにより，

\begin{aligned} F (i, j) = \frac{Γ (i + j + α)}{Γ (i + 1 + α) Γ (j)} x^{i} (1 - x)^{j} \\ G (i, j) = - \frac{Γ (i + j + α)}{Γ (i + α) Γ (j + 1)} x^{i} (1 - x)^{j} \end{aligned}

が $WZ-pair$ とわかります。いま， $(0, 0)$ から $(m, 0)$ までの重み

\begin{array}{r} \sum_{i = 0}^{m - 1} F (i, 0) \end{array}

を考えるとき，

\begin{array}{r} F (i, 0) = \frac{Γ (i + α)}{Γ (i + 1 + α) Γ (0)} x^{i} \end{array}

となり，分母に $Γ (0)$ が出現します。そこで， $F, G$ に周期 $1$ の

\begin{array}{r} e (j) = (- 1)^{j} Γ (j) Γ (1 - j) = \frac{π (- 1)^{j}}{\sin π j} \end{array}

を掛ければ， $(e (j) F (i, j), e (j) G (i, j))$ は $WZ-pair$ となります。これを $S h a d o w i n g$ といいます。
すなわち，

\begin{aligned} F (i, j) = \frac{Γ (i + j + α) Γ (1 - j)}{Γ (i + 1 + α)} x^{i} (x - 1)^{j} \\ G (i, j) = \frac{Γ (i + j + α) Γ (- j)}{Γ (i + α)} x^{i} (x - 1)^{j} \end{aligned}

と改めます。

$T h r e e P a t h s W a y 1$

　次の経路を考えます。

赤の経路と緑の経路の重みを足し合わせると，青の経路の重みと等しくなります。また，青経路と緑経路はそれぞれ横軸と縦軸に沿って進みます。
証明は省きますが，この経路で $n \to \infty$ とすれば，緑の重みは $0$ になります。
いま，赤経路上で $(0, 0)$ に最も近い格子点を $(p, - q)$ とし， $(k p, - k q) \to ((k + 1) p, - (k + 1) q)$ の重みを $H_{p, q} (k)$ とします。
このとき，

\begin{array}{r} \sum_{i = 0}^{\infty} F (i, 0) = \sum_{k = 0}^{\infty} H_{p, q} (k) \end{array}

であり， $H_{p, q} (k)$ は

\begin{aligned} H_{p, q} (k) & = \sum_{i = k p}^{(k + 1) p - 1} F (i, - (k + 1) q) - \sum_{j = - (k + 1) q}^{- k q - 1} G (k p, j) \\ = \sum_{i = 0}^{p - 1} F (i + k p, - (k + 1) q) - \sum_{j = 0}^{q - 1} G (k p, j - (k + 1) q) \end{aligned}

となります。 $F (i, 0) = \frac{x^{i}}{i + α}$ です。 $H_{p, q} (k)$ はどうなるでしょうか。
一般の $H_{p, q} (k)$ を求めるのは困難かもしれませんが，具体的な $p, q$ に対して計算してみます。

\begin{aligned} H_{1, 1} (k) & = \sum_{i = 0}^{0} F (i + k, - (k + 1)) - \sum_{j = 0}^{0} G (k, j - (k + 1)) \\ = F (k, - (k + 1)) - G (k, - (k + 1)) \\ = \frac{Γ (- 1 + α) Γ (k + 2)}{Γ (k + α + 1)} x^{k} (x - 1)^{- k - 1} - \frac{Γ (- 1 + α) Γ (k + 1)}{Γ (k + α)} x^{k} (x - 1)^{- k - 1} \\ = \frac{Γ (- 1 + α) k!}{Γ (k + α + 1)} x^{k} (x - 1)^{- k - 1} (k + 1 - (k + α)) \\ = - \frac{Γ (α) k!}{Γ (k + α + 1)} x^{k} (x - 1)^{- k - 1} \\ = \frac{1}{α (1 - x)} \frac{k!}{(1 + α)_{k}} {(\frac{x}{x - 1})}^{k} \end{aligned}

\begin{aligned} H_{2, 1} (k) & = \sum_{i = 0}^{1} F (i + 2 k, - (k + 1)) - \sum_{j = 0}^{0} G (2 k, j - (k + 1)) \\ = F (2 k, - (k + 1)) + F (2 k + 1, - (k + 1)) - G (2 k, - (k + 1)) \\ = \frac{Γ (k + α - 1) Γ (k + 2)}{Γ (2 k + α + 1)} x^{2 k} (x - 1)^{- k - 1} + \frac{Γ (k + α) Γ (k + 2)}{Γ (2 k + α + 2)} x^{2 k + 1} (x - 1)^{- k - 1} - \frac{Γ (k + α - 1) Γ (k + 1)}{Γ (2 k + α)} x^{2 k} (x - 1)^{- k - 1} \\ = \frac{Γ (k + α - 1) k!}{Γ (2 k + α + 2)} x^{2 k} (x - 1)^{- k - 1} ((k + 1) (2 k + α + 1) + (k + 1) (k + α - 1) x - (2 k + α) (2 k + α + 1)) \\ = \frac{Γ (k + α - 1) k!}{Γ (2 k + α + 2)} x^{2 k} (x - 1)^{- k - 1} ((k + 1 - (2 k + α)) (2 k + α + 1) + (k + 1) (k + α - 1) x) \\ = \frac{Γ (k + α - 1) k!}{Γ (2 k + α + 2)} x^{2 k} (x - 1)^{- k - 1} ((- k - α + 1) (2 k + α + 1) + (k + 1) (k + α - 1) x) \\ = - \frac{Γ (k + α) k!}{Γ (2 k + α + 2)} x^{2 k} (x - 1)^{- k - 1} ((2 k + α + 1) - (k + 1) x) \\ = \frac{1}{α (1 + α) (1 - x)} ((2 - x) k + 1 - x + α) \frac{(α)_{k} k!}{(2 + α)_{2 k}} {(\frac{x^{2}}{x - 1})}^{k} \end{aligned}

\begin{aligned} H_{1, 2} (k) & = \sum_{i = 0}^{0} F (i + k, - 2 (k + 1)) - \sum_{j = 0}^{1} G (k, j - 2 (k + 1)) \\ = F (k, - (2 k + 2)) - G (k, - (2 k + 2)) - G (k, - (2 k + 1)) \\ = \frac{Γ (- k + α - 2) Γ (2 k + 3)}{Γ (k + α + 1)} x^{k} (x - 1)^{- 2 k - 2} - \frac{Γ (- k + α - 2) Γ (2 k + 2)}{Γ (k + α)} x^{k} (x - 1)^{- 2 k - 2} - \frac{Γ (- k + α - 1) Γ (2 k + 1)}{Γ (k + α)} x^{k} (x - 1)^{- 2 k - 1} \\ = \frac{Γ (- k + α - 2) (2 k)!}{Γ (k + α + 1)} x^{k} (x - 1)^{- 2 k - 2} ((2 k + 1) (2 k + 2) - (2 k + 1) (k + α) - (- k + α - 2) (k + α) (x - 1)) \\ = \frac{Γ (- k + α - 2) (2 k)!}{Γ (k + α + 1)} x^{k} (x - 1)^{- 2 k - 2} ((2 k + 1) (k - α + 2) - (- k + α - 2) (k + α) (x - 1)) \\ = - \frac{Γ (- k + α - 1) (2 k)!}{Γ (k + α + 1)} x^{k} (x - 1)^{- 2 k - 2} (2 k + 1 + (k + α) (x - 1)) \\ = - \frac{Γ (α - 1)}{Γ (1 + α)} ((1 + x) k + 1 + α (x - 1)) \frac{(α - 1)_{- k} (2 k)!}{(1 + α)_{k}} {(\frac{x}{(1 - x)^{2}})}^{k} \frac{1}{(1 - x)^{2}} \\ = \frac{1}{α (1 - α) (1 - x)^{2}} ((1 + x) k + 1 + α (x - 1)) \frac{(2 k)!}{(1 + α)_{k} (2 - α)_{k}} {(\frac{- x}{(1 - x)^{2}})}^{k} \end{aligned}

\begin{aligned} H_{2, 2} (k) & = \sum_{i = 0}^{1} F (i + 2 k, - 2 (k + 1)) - \sum_{j = 0}^{1} G (2 k, j - 2 (k + 1)) \\ = F (2 k, - (2 k + 2)) + F (2 k + 1, - (2 k + 2)) - G (2 k, - (2 k + 2)) - G (2 k, - (2 k + 1)) \\ = \frac{Γ (α - 2) Γ (2 k + 3)}{Γ (2 k + α + 1)} x^{2 k} (x - 1)^{- 2 k - 2} + \frac{Γ (α - 1) Γ (2 k + 3)}{Γ (2 k + α + 2)} x^{2 k + 1} (x - 1)^{- 2 k - 2} - \frac{Γ (α - 2) Γ (2 k + 2)}{Γ (2 k + α)} x^{2 k} (x - 1)^{- 2 k - 2} - \frac{Γ (α - 1) Γ (2 k + 1)}{Γ (2 k + α)} x^{2 k} (x - 1)^{- 2 k - 1} \\ = \frac{Γ (α - 2) (2 k)!}{Γ (2 k + α + 2)} x^{2 k} (x - 1)^{- 2 k - 2} ((2 k + 1) (2 k + 2) (2 k + α + 1) + (α - 2) (2 k + 1) (2 k + 2) x - (2 k + 1) (2 k + α) (2 k + α + 1) - (α - 2) (2 k + α) (2 k + α + 1) (x - 1)) \\ = \frac{Γ (α - 2) (2 k)!}{Γ (2 k + α + 2)} x^{2 k} (x - 1)^{- 2 k - 2} ((2 k + 1) (2 k + α + 1) (2 - α) + (α - 2) (2 k + α) (2 k + α + 1) + (α - 2) ((2 k + 1) (2 k + 2) - (2 k + α) (2 k + α + 1)) x) \\ = \frac{Γ (α - 2) (2 k)!}{Γ (2 k + α + 2)} x^{2 k} (x - 1)^{- 2 k - 2} ((α - 2) (α - 1) (2 k + α + 1) + (α - 2) ((2 k + 1) (2 k + 2) - (2 k + α) (2 k + α + 1)) x) \\ = \frac{Γ (α - 1) (2 k)!}{Γ (2 k + α + 2)} x^{2 k} (x - 1)^{- 2 k - 2} ((α - 1) (2 k + α + 1) + (1 - α) (4 k + α + 2) x) \\ = \frac{Γ (α) (2 k)!}{Γ (2 k + α + 2)} x^{2 k} (x - 1)^{- 2 k - 2} (2 k + α + 1 - (4 k + α + 2) x) \\ = \frac{Γ (α)}{Γ (2 + α)} (2 k + α + 1 - (4 k + α + 2) x) \frac{(2 k)!}{(2 + α)_{2 k}} {(\frac{x}{x - 1})}^{2 k} \frac{1}{(1 - x)^{2}} \\ = \frac{1}{α (1 + α) (1 - x)^{2}} (2 (1 - 2 x) k + (1 - x) (2 + α) - 1) \frac{(2 k)!}{(2 + α)_{2 k}} {(\frac{x}{1 - x})}^{2 k} \end{aligned}

このようになります。まとめると

<p style=" margin: 0; padding: 0; "

\begin{aligned} \sum_{n = 0}^{\infty} \frac{x^{n}}{n + α} & = \frac{1}{α (1 - x)} \sum_{n = 0}^{\infty} \frac{n!}{(1 + α)_{n}} {(\frac{x}{x - 1})}^{n} \\ = \frac{1}{α (1 + α) (1 - x)} \sum_{n = 0}^{\infty} ((2 - x) n + 1 - x + α) \frac{(α)_{n} n!}{(2 + α)_{2 n}} {(\frac{x^{2}}{x - 1})}^{n} \\ = \frac{1}{α (1 - α) (1 - x)^{2}} \sum_{n = 0}^{\infty} ((1 + x) n + 1 + α (x - 1)) \frac{(2 n)!}{(1 + α)_{n} (2 - α)_{n}} {(\frac{- x}{(1 - x)^{2}})}^{n} \\ = \frac{1}{α (1 + α) (1 - x)^{2}} \sum_{n = 0}^{\infty} (2 (1 - 2 x) n + (1 - x) (2 + α) - 1) \frac{(2 n)!}{(2 + α)_{2 n}} {(\frac{x}{1 - x})}^{2 n} \end{aligned}

となります。
例えば２行目の式において， $α$ で微分し $x = - 1, α = 1$ を代入すると

\begin{array}{r} \sum_{n = 1}^{\infty} \frac{(- 1)^{n - 1}}{n^{2}} = \sum_{n = 1}^{\infty} \frac{(- 1)^{n - 1}}{2^{n} n (\binom{2 n}{n})} (\frac{2}{n} + 3 (H_{2 n} - H_{n})) \end{array}

という式が得られます。

$T h r e e P a t h s W a y 2$

　 $WZ-pair$

\begin{aligned} F (i, j) = \frac{H (i, j)}{i} \\ G (i, j) = - \frac{H (i, j)}{j} \\ H (i, j) = \frac{Γ (i + j)}{Γ (i) Γ (j)} z^{i} (1 - z)^{j} (0 < z < \frac{1}{2}) \end{aligned}

に対して，次の経路を考えます。

前述と同様に， $n \to \infty$ において緑の重みは $0$ に収束します。
赤の経路上で $(s, t)$ に最も近い格子点を $(s + p, t + q)$ とし， $(s + k p, t + k q) \to (s + (k + 1) p, t + (k + 1) q)$ の重みを $H_{p, q} (k)$ とします。
このとき，

\begin{array}{r} \sum_{m = 0}^{\infty} F (s + m, t) = \sum_{k = 0}^{\infty} H_{p, q} (k) \end{array}

であり， $H_{p, q} (k)$ は

\begin{aligned} H_{p, q} (k) & = \sum_{n = 0}^{p - 1} F (s + k p + n, t + k q) + \sum_{n = 0}^{q - 1} G (s + (k + 1) p, t + k q + n) \end{aligned}

となります。実際に $H_{p, q} (k) を計算すると$

\begin{aligned} H_{1, 1} (k) & = \frac{Γ (s + t - 2)}{Γ (s) Γ (t)} (A_{1, 1} + B_{1, 1} (k + 1)) \frac{(s + t - 2)_{2 k + 2}}{(s)_{k + 1} (t)_{k + 1}} z^{s + k} (1 - z)^{t + k} \\ H_{2, 1} (k) & = \frac{Γ (s + t - 2)}{Γ (s) Γ (t)} (A_{2, 1} + B_{2, 1} (k + 1) + C_{2, 1} (k + 1)^{2}) \frac{(s + t - 2)_{3 k + 2}}{(s)_{2 k + 2} (t)_{k + 1}} z^{s + 2 k} (1 - z)^{t + k} \\ H_{1, 2} (k) & = \frac{Γ (s + t - 2)}{Γ (s) Γ (t)} (A_{1, 2} + B_{1, 2} (k + 1) + C_{1, 2} (k + 1)^{2}) \frac{(s + t - 2)_{3 k + 2}}{(s)_{k + 1} (t)_{2 k + 2}} z^{s + k} (1 - z)^{t + 2 k} \end{aligned}

\begin{aligned} (\begin{array}{c} A_{1, 1} \\ B_{1, 1} \end{array}) & = (\begin{array}{c} t - 1 - (s + t - 2) z \\ 1 - 2 z \end{array}) \\ (\begin{array}{c} A_{2, 1} \\ B_{2, 1} \\ C_{2, 1} \end{array}) & = (\begin{array}{c} (s - 1) (t - 1) - (3 - s - t) (t - 1) z + (s + t - 2) (3 - s - t) z^{2} \\ s + 2 t - 3 - (6 - s - 4 t) z + 3 (5 - 2 s - 2 t) z^{2} \\ (1 + 3 z) (2 - 3 z) \end{array}) \\ (\begin{array}{c} A_{1, 2} \\ B_{1, 2} \\ C_{1, 2} \end{array}) & = (\begin{array}{c} - (t - 1) (2 - t) + (3 - s - t) (s + 2 t - 3) z - (s + t - 2) (3 - s - t) z^{2} \\ - 2 (3 - 2 t) + (24 - 8 s - 11 t) z - 3 (5 - 2 s - 2 t) z^{2} \\ (1 - 3 z) (2 - 3 z) \end{array}) \end{aligned}

となります。 $s, t$ に $1$ を足し， $F, H$ の和を $1$ からとるように調整すると

\begin{aligned} (s + t) \sum_{m = 1}^{\infty} \frac{(1 + s + t)_{n}}{(1 + s)_{n}} z^{n - 1} & = \sum_{k = 1}^{\infty} (A_{1, 1}^{'} + B_{1, 1}^{'} k) \frac{(s + t)_{2 k}}{(1 + s)_{k} (1 + t)_{k}} z^{k - 1} (1 - z)^{k - 1} \\ = \sum_{k = 1}^{\infty} (A_{2, 1}^{'} + B_{2, 1}^{'} k + C_{2, 1}^{'} k^{2}) \frac{(s + t)_{3 k - 1}}{(1 + s)_{2 k} (1 + t)_{k}} z^{2 k - 2} (1 - z)^{k - 1} \\ = \sum_{k = 1}^{\infty} (A_{1, 2}^{'} + B_{1, 2}^{'} k + C_{1, 2}^{'} k^{2}) \frac{(s + t)_{3 k - 1}}{(1 + s)_{k} (1 + t)_{2 k}} z^{k - 1} (1 - z)^{2 k - 2} \end{aligned}

\begin{aligned} (\begin{array}{c} A_{1, 1}^{'} \\ B_{1, 1}^{'} \end{array}) & = (\begin{array}{c} t - (s + t) z \\ 1 - 2 z \end{array}) \\ (\begin{array}{c} A_{2, 1}^{'} \\ B_{2, 1}^{'} \\ C_{2, 1}^{'} \end{array}) & = (\begin{array}{c} s t - t (1 - s - t) z + (s + t) (1 - s - t) z^{2} \\ s + 2 t - (1 - s - 4 t) z + 3 (1 - 2 s - 2 t) z^{2} \\ (1 + 3 z) (2 - 3 z) \end{array}) \\ (\begin{array}{c} A_{1, 2}^{'} \\ B_{1, 2}^{'} \\ C_{1, 2}^{'} \end{array}) & = (\begin{array}{c} - t (1 - t) + (1 - s - t) (s + 2 t) z - (s + t) (1 - s - t) z^{2} \\ - 2 (1 - 2 t) + (5 - 8 s - 11 t) z - 3 (1 - 2 s - 2 t) z^{2} \\ (1 - 3 z) (2 - 3 z) \end{array}) \end{aligned}

$z^{s} (1 - z)^{t}$ を除いたので， $z$ を負に拡張できます。すべての等式が成り立つにはより狭い

\begin{array}{r} - \frac{1}{3} (2 - (- 1 + \sqrt{2})^{- \frac{2}{3}} - (- 1 + \sqrt{2})^{\frac{2}{3}}) \leq z < \frac{1}{3} \end{array}

である必要があります。

$t e l e s c o p i n g s u m$

　経路不変性

\begin{array}{r} F (i, j) - F (i, j + 1) = G (i, j) - G (i + 1, j) \end{array}

において， $j$ に $j + 1, j + 2, \dots, j + m$ を代入したものを辺辺足し合わせると

\begin{array}{r} F (i, j) - F (i, j + m + 1) = \sum_{n = 0}^{m} (G (i, j + n) - G (i + 1, j + n)) \end{array}

となります。いま $F (i, \infty) = 0$ と仮定すれば

\begin{array}{r} F (i, j) = \sum_{n = 0}^{\infty} (G (i, j + n) - G (i + 1, j + n)) \end{array}

となります。
同様に， $i$ に $i + 1, i + 2, \dots, i + m$ を代入して

\begin{array}{r} \sum_{n = 0}^{m} (F (i + n, j) - F (i + n, j + 1)) = G (i, j) - G (i + m + 1, j) \end{array}

となり， $G (\infty, j) = 0$ とすれば

\begin{array}{r} \sum_{n = 0}^{\infty} (F (i + n, j) - F (i + n, j + 1)) = G (i, j) \end{array}

となります。ここからさらに $j$ に $j + 1, j + 2, \dots, j + m$ を代入して足し合わせれば

\begin{array}{r} \sum_{n = 0}^{\infty} (F (i + n, j) - F (i + n, j + m + 1)) = \sum_{n = 0}^{m} G (i, j + n) \end{array}

となり， $lim_{m \to \infty} \sum_{n = 0}^{\infty} F (i + n, j + m) = 0$ と仮定すれば

\begin{array}{r} \sum_{n = 0}^{\infty} F (i + n, j) = \sum_{n = 0}^{\infty} G (i, j + n) \end{array}

となります。

$Markov-WZ m e t h o d$

　一般に $h y p e r g e o m e t r i c t e r m$ としての $WZ-pair$ を見つけることは，私にとっては難しいものです。しかし，その $t e r m$ にパラメータの多項式を掛けたものを見つけるためのアルゴリズムがあり，それにより原理としては容易に $WZ-pair$ を見つけることができました。
　そのアルゴリズムは

１．

m, n

の関数

H (m, n)

をテキトーに決める
２．

\begin{aligned} F (m, n) & = (A_{0} (n) + m A_{1} (n) + \dots + m^{p} A_{p} (n)) H (m, n) \\ G (m, n) & = (B_{0} (n) + m B_{1} (n) + \dots + m^{q} B_{q} (n)) H (m, n) \end{aligned}

と定義する
３．

F (m, n) - F (m, n + 1) = G (m, n) - G (m + 1, n)

に代入し，

(m + 1)^{r}

の係数比較から

A_{1} (n), \dots, B_{q} (n)

を求める

です。無限級数としての等式を得たいというときは， $F (\infty, x)$ や $G (x, \infty)$ などがうまく $0$ に収束するように $H (m, n)$ を決定する必要があります。
具体例で計算してみます。
まず

\begin{array}{r} H (m, n) = {(\frac{m! n!}{(m + n)!})}^{2} \end{array}

と定義し，

\begin{aligned} F (m, n) & = A (n) H (m, n) \\ G (m, n) & = (B (n) + m C (n)) H (m, n) \end{aligned}

と定義します。
このとき

\begin{aligned} F (m, n) - F (m, n + 1) & = A (n) H (m, n) - A (n + 1) H (m, n + 1) \\ = A (n) H (m, n) - A (n + 1) \frac{(n + 1)^{2}}{(m + n + 1)^{2}} H (m, n) \\ = ((m + n + 1)^{2} A (n) - (n + 1)^{2} A (n + 1)) \frac{H (m, n)}{(m + n + 1)^{2}} \\ = (n^{2} A (n) - (n + 1)^{2} A (n + 1) + 2 (m + 1) n A (n) + (m + 1)^{2} A (n)) \frac{H (m, n)}{(m + n + 1)^{2}} \end{aligned}

また

\begin{aligned} G (m, n) - G (m + 1, n) & = (B (n) + m C (n)) H (m, n) - (B (n) + (m + 1) C (n)) H (m + 1, n) \\ = (B (n) - C (n) + (m + 1) C (n)) H (m, n) - (B (n) + (m + 1) C (n)) \frac{(m + 1)^{2}}{(m + n + 1)^{2}} H (m, n) \\ = ((m + n + 1)^{2} (B (n) - C (n) + (m + 1) C (n)) - (m + 1)^{2} (B (n) + (m + 1) C (n))) \frac{H (m, n)}{(m + n + 1)^{2}} \\ = ((n^{2} + 2 (m + 1) n + (m + 1)^{2}) (B (n) - C (n) + (m + 1) C (n)) - (m + 1)^{2} B (n) - (m + 1)^{3} C (n)) \frac{H (m, n)}{(m + n + 1)^{2}} \\ = (n^{2} (B (n) - C (n)) + (2 n (B (n) - C (n)) + n^{2} C (n)) (m + 1) + (B (n) - C (n) + 2 n C (n)) (m + 1)^{2} + (m + 1)^{3} C (n) - (m + 1)^{2} B (n) - (m + 1)^{3} C (n)) \frac{H (m, n)}{(m + n + 1)^{2}} \\ = (n^{2} B (n) - n^{2} C (n) + (2 n B (n) + (n^{2} - 2 n) C (n)) (m + 1) + (m + 1)^{2} (2 n - 1) C (n)) \frac{H (m, n)}{(m + n + 1)^{2}} \end{aligned}

となります。係数比較により

\begin{array}{r} {\begin{cases} n^{2} A (n) - (n + 1)^{2} A (n + 1) = n^{2} B (n) - n^{2} C (n) \\ 2 n A (n) = 2 n B (n) + (n^{2} - 2 n) C (n) \\ A (n) = (2 n - 1) C (n) \end{cases} \end{array}

を得ます。これを解くと

\begin{array}{r} A (n) = \frac{2 (2 n - 1)}{n^{3} (\binom{2 n}{n})} A (1), B (n) = \frac{3 n A (n)}{2 (2 n - 1)}, C (n) = \frac{A (n)}{2 n - 1} \end{array}

となります。 $A (1)$ は $F$ と $G$ の比に影響しないので適当に $1$ としてよいです。
すなわち，

\begin{aligned} F (m, n) & = \frac{2 (2 n - 1)}{n^{3} (\binom{2 n}{n})} {(\frac{m! n!}{(m + n)!})}^{2} \\ G (m, n) & = \frac{2 m + 3 n}{n^{3} (\binom{2 n}{n})} {(\frac{m! n!}{(m + n)!})}^{2} \end{aligned}

が $WZ-pair$ であることがわかりました。
実はこの方法は $Markov-WZ m e t h o d$ と呼ばれるらしいです。
この $WZ-pair$ に対して， $t e l e s c o p i n g s u m$ を考えると，

\begin{array}{r} \sum_{m = 0}^{\infty} F (m + α, β) = \sum_{n = 0}^{\infty} G (α, n + β) \end{array}

すなわち

\begin{array}{r} \sum_{m = 0}^{\infty} \frac{(1 + α)_{m}^{2}}{(1 + α + β)_{m}^{2}} = \frac{β^{4} Γ (β)}{2 (2 β - 1)} \sum_{n = 0}^{\infty} \frac{2 α + 3 β + 3 n}{(β + n)^{3}} \frac{(1 + β)_{n}^{4}}{(1 + 2 β)_{2 n} (1 + α + β)_{n}^{2}} (β > \frac{1}{2}) \end{array}

となります。 $β = 1$ の場合は

\begin{array}{r} \sum_{n = 1}^{\infty} \frac{1}{(n + α)^{2}} = \sum_{n = 1}^{\infty} \frac{3 n + 2 α}{n^{3} (\binom{2 n}{n})} \frac{n!^{2}}{(1 + α)_{n}^{2}} \end{array}

となります。
また， $t h r e e p a t h s w a y$ により

\begin{array}{r} \sum_{n = 0}^{\infty} F (n + α, β) = \sum_{n = 0}^{\infty} H_{p, q} (n) \end{array}

\begin{array}{r} H_{p, q} (n) = \sum_{j = 0}^{p - 1} F (α + p n + j, β + q n) + \sum_{k = 0}^{q - 1} G (α + p n + p, β + q n + k) \end{array}

となり，実際に $H_{1, 1} (n)$ を計算すると

\begin{array}{r} H_{1, 1} (n) = \frac{Γ^{2} (1 + α) Γ^{4} (1 + β)}{Γ (1 + 2 β) Γ^{2} (1 + α + β)} \frac{A + B n + C n^{2} + 21 n^{3}}{(β + n)^{3}} \frac{(1 + α)_{n}^{2} (1 + β)_{n}^{4}}{(1 + 2 β)_{2 n} (1 + α + β)_{2 n}^{2}} \end{array}

\begin{array}{r} (\begin{array}{c} A \\ B \\ C \end{array}) = (\begin{array}{c} 2 (2 β - 1) (1 + α + β)^{2} + (2 + 2 α + 3 β) (1 + α)^{2} \\ 8 (2 β - 1) (1 + α + β) + 4 (1 + α + β)^{2} + 2 (2 + 2 α + 3 β) (1 + α) + 5 (1 + α)^{2} \\ 8 (2 β - 1) + 16 (1 + α + β) + 10 (1 + α) + 2 + 2 α + 3 β \end{array}) \end{array}

となりました。 $H_{1, 2} (n), H_{2, 1} (n)$ 以降は計算量が多すぎて心が折れました。
$α$ と $β$ に具体的な数値を代入すると少し計算しやすくなるので， $α = 0, β = 1$ で計算してみると

\begin{aligned} H_{1, 1} (n - 1) & = \frac{21 n - 8}{n^{3} {(\binom{2 n}{n})}^{3}} \\ H_{1, 2} (n - 1) & = \frac{145 n^{2} - 104 n + 18}{2 n^{3} (2 n - 1) (\binom{2 n}{n}) {(\binom{3 n}{n})}^{2}} \\ H_{2, 1} (n - 1) & = \frac{9}{4} \frac{80 n^{3} - 105 n^{2} + 44 n - 6}{n^{2} (2 n - 1)^{3} {(\binom{3 n}{n})}^{2} (\binom{4 n - 2}{2 n - 1})} + \frac{1}{n^{2} {(\binom{3 n}{n})}^{2} (\binom{4 n}{2 n})} \\ H_{2, 2} (n - 1) & = \frac{4 (680 n^{5} - 1236 n^{4} + 846 n^{3} - 281 n^{2} + 46 n - 3)}{(2 n - 1)^{5} (4 n - 1)^{2} (\binom{4 n - 2}{2 n - 1}) {(\binom{4 n}{2 n})}^{2}} + \frac{5}{4 n^{2} {(\binom{4 n}{2 n})}^{3}} \end{aligned}

$p + q$ が大きくなるにつれて，収束が速くなります。
なんというか，コンピュータが全部計算してくれるみたいなことはできないのでしょうか。流石に手計算はキツいです。もしできたら，

\begin{array}{r} H (m, n) = {(\frac{m! n!}{(m + n)!})}^{5} \end{array}

のような場合の $WZ-pair$ がどのようなかたちになるかもわかりますが。

$p a r a m e t e r i z e d$

まず

\begin{array}{r} H (m, n) = \frac{Γ (a + m) Γ (b + m)}{Γ (c + m + n) Γ (d + m + n)} \end{array}

と定義します。さらに

\begin{aligned} F (m, n) = A (n) H (m, n) \\ G (m, n) = (B (n) + m C (n)) H (m, n) \end{aligned}

と定義します。

\begin{aligned} F (m, n) - F (m, n + 1) & = A (n) H (m, n) - A (n + 1) H (m, n + 1) \\ = A (n) H (m, n) - A (n + 1) \frac{H (m, n)}{(c + m + n) (d + m + n)} \\ = ((c + m + n) (d + m + n) A (n) - A (n + 1)) \frac{H (m, n)}{(c + m + n) (d + m + n)} \\ = (m^{2} A (n) + (c + d + 2 n) m A (n) + (c + n) (d + n) A (n) - A (n + 1)) \frac{H (m, n)}{(c + m + n) (d + m + n)} \end{aligned}

\begin{aligned} G (m, n) - G (m + 1, n) & = (B (n) + m C (n)) H (m, n) - (B (n) + (m + 1) C (n)) \frac{(a + m) (b + m) H (m, n)}{(c + m + n) (d + m + n)} \\ = ((c + m + n) (d + m + n) (B (n) + m C (n)) - (a + m) (b + m) (B (n) + (m + 1) C (n))) \frac{H (m, n)}{(c + m + n) (d + m + n)} \\ = (\begin{array}{c} ((c + n) (d + n) + (c + d + 2 n) m + m^{2}) (B (n) + m C (n)) \\ - (a b + (a + b) m + m^{2}) (B (n) + C (n) + m C (n)) \end{array}) \frac{H (m, n)}{(c + m + n) (d + m + n)} \\ = ((c + d - a - b - 1 + 2 n) m^{2} C (n) + ((c + d - a - b + 2 n) B (n) + ((c + n) (d + n) - a - b - a b)) m C (n) + ((c + n) (d + n) - a b) B (n) - a b C (n)) \frac{H (m, n)}{(c + m + n) (d + m + n)} \end{aligned}

すなわち， $(F, G)$ が $WZ-pair$ となるように

\begin{array}{r} {\begin{cases} A (n) = (c + d - a - b - 1 + 2 n) C (n) \\ (c + d + 2 n) A (n) = (c + d - a - b + 2 n) B (n) + ((c + n) (d + n) - a - b - a b) C (n) \\ (c + n) (d + n) A (n) - A (n + 1) = ((c + n) (d + n) - a b) B (n) - a b C (n) \end{cases} \end{array}

を解くと，

\begin{array}{r} {\begin{cases} A (n) = \frac{(c - a)_{n} (c - b)_{n} (d - a)_{n} (d - b)_{n}}{(c + d - a - b - 1)_{2 n}} \\ B (n) = \frac{3 n^{2} + p n + q}{(c + d - a - b - 1 + 2 n) (c + d - a - b + 2 n)} A (n) (\begin{array}{c} p = 3 c + 3 d - 2 a - 2 b - 2 \\ q = (c + d) (c + d - a - b - 1) + a + b + a b - c d \end{array}) \\ C (n) = \frac{A (n)}{c + d - a - b - 1 + 2 n} \end{cases} \end{array}

となります。
ここで

\begin{aligned} \sum_{m = 0}^{\infty} F (m + α, 1 + β) & = \sum_{m = 0}^{\infty} \frac{(c - a)_{1 + β} (c - b)_{1 + β} (d - a)_{1 + β} (d - b)_{1 + β}}{(c + d - a - b - 1)_{2 + 2 β}} \frac{Γ (a + α + m) Γ (b + α + m)}{Γ (1 + c + α + m) Γ (1 + d + α + m)} \\ = \frac{Γ (c + d - a - b - 1) Γ (c - a + 1 + β) Γ (c - b + 1 + β) Γ (d - a + 1 + β) Γ (d - b + 1 + β) Γ (a + α) Γ (b + α)}{Γ (c - a) Γ (c - b) Γ (d - a) Γ (d - b) Γ (c + d - a - b + 1 + 2 β) Γ (c + α) Γ (d + α)} \sum_{m = 1}^{\infty} \frac{1}{(m - 1 + a + α) (m - 1 + b + α)} \frac{(a + α)_{m} (b + α)_{m}}{(c + α)_{m} (d + α)_{m}} \end{aligned}

また

\begin{aligned} \sum_{n = 1}^{\infty} G (α, n + β) & = \sum_{n = 1}^{\infty} (\frac{3 (n + β)^{2} + p (n + β) + q}{(c + d - a - b - 1 + 2 β + 2 n) (c + d - a - b + 2 β + 2 n)} + \frac{α}{c + d - a - b - 1 + 2 β + 2 n}) \frac{(c - a)_{n + β} (c - b)_{n + β} (d - a)_{n + β} (d - b)_{n + β}}{(c + d - a - b - 1)_{2 n + 2 β}} \frac{Γ (a + α) Γ (b + α)}{Γ (c + α + β + n) Γ (d + α + β + n)} \\ = \frac{Γ (c - a + β) Γ (c - b + β) Γ (d - a + β) Γ (d - b + β) Γ (c + d - a - b - 1) Γ (a + α) Γ (b + α)}{Γ (c - a) Γ (c - b) Γ (d - a) Γ (d - b) Γ (c + d - a - b + 1 + 2 β) Γ (c + α + β) Γ (d + α + β)} \sum_{n = 1}^{\infty} (3 n^{2} + (2 α + 6 β + p) n + 3 β^{2} + p β + q + α (c + d - a - b + 2 β)) \frac{(c - a + β)_{n} (c - b + β)_{n} (d - a + β)_{n} (d - b + β)_{n}}{(c + d - a - b + 1 + 2 β)_{2 n} (c + α + β)_{n} (d + α + β)_{n}} \end{aligned}

となるので

\begin{aligned} \sum_{m = 1}^{\infty} \frac{1}{(m - 1 + a + α) (m - 1 + b + α)} \frac{(a + α)_{m} (b + α)_{m}}{(c + α)_{m} (d + α)_{m}} \\ = & \frac{Γ (c + α) Γ (d + α)}{Γ (c + α + β) Γ (d + α + β)} \sum_{n = 1}^{\infty} (3 n^{2} + (2 α + 6 β + p) n + 3 β^{2} + p β + q + α (c + d - a - b + 2 β)) \frac{(1 + c - a + β)_{n - 1} (1 + c - b + β)_{n - 1} (1 + d - a + β)_{n - 1} (1 + d - b + β)_{n - 1}}{(c + d - a - b + 1 + 2 β)_{2 n} (c + α + β)_{n} (d + α + β)_{n}} \end{aligned}

(p = 3 c + 3 d - 2 a - 2 b - 2, q = (c + d) (c + d - a - b - 1) + a + b + a b - c d)

　
$c = a, d = b, α = β = 0$ とすると $p = a + b - 2, q = 0$ となり

\begin{array}{r} \sum_{m = 1}^{\infty} \frac{1}{(m - 1 + a) (m - 1 + b)} = \sum_{n = 1}^{\infty} \frac{3 n + a + b - 2}{n (\binom{2 n}{n})} \frac{(1 + a - b)_{n - 1} (1 - a + b)_{n - 1}}{(a)_{n} (b)_{n}} \end{array}

$a \to 1 - a, b \to 1 - b$ とすれば

\begin{array}{r} \sum_{m = 1}^{\infty} \frac{1}{(m - a) (m - b)} = \sum_{n = 1}^{\infty} \frac{3 n - a - b}{n (\binom{2 n}{n})} \frac{(1 + a - b)_{n - 1} (1 - a + b)_{n - 1}}{(1 - a)_{n} (1 - b)_{n}} \end{array}

さらに $b = - a$ とすれば

\begin{aligned} \sum_{m = 1}^{\infty} \frac{1}{m^{2} - a^{2}} & = \sum_{n = 1}^{\infty} \frac{3}{(\binom{2 n}{n})} \frac{(1 + 2 a)_{n - 1} (1 - 2 a)_{n - 1}}{(1 + a)_{n} (1 - a)_{n}} \\ = \sum_{n = 1}^{\infty} \frac{3}{(\binom{2 n}{n}) (n^{2} - a^{2})} \prod_{k = 1}^{n - 1} \frac{k^{2} - 4 a^{2}}{k^{2} - a^{2}} \end{aligned}

これは冒頭の公式です。

$a c c e l e r a t e d s e r i e s f o r ζ (3)$

まず， $m, n \geq 0$ とします。

\begin{array}{r} H (m, n) = {(\frac{n!}{(m + n + 1)!})}^{4} \end{array}

とし，

\begin{aligned} F (m, n) = (A_{m} + n B_{m} + n^{2} C_{m} + n^{3} D_{m}) H (m, n) \\ G (m, n) = (P_{m} + (n + 1) Q_{m} + (n + 1)^{2} R_{m}) H (m, n) \end{aligned}

と定義します。

\begin{aligned} F (m, n) - F (m, n + 1) & = (A_{m} + n B_{m} + n^{2} C_{m} + n^{3} D_{m}) H (m, n) - (A_{m} + (n + 1) B_{m} + (n + 1)^{2} C_{m} + (n + 1)^{3} D_{m}) H (m, n + 1) \\ = ((m + n + 2)^{4} (A_{m} + n B_{m} + n^{2} C_{m} + n^{3} D_{m}) - (n + 1)^{4} (A_{m} + (n + 1) B_{m} + (n + 1)^{2} C_{m} + (n + 1)^{3} D_{m})) \frac{H (m, n)}{(m + n + 2)^{4}} \end{aligned}

\begin{aligned} G (m, n) - G (m + 1, n) & = (P_{m} + (n + 1) Q_{m} + (n + 1)^{2} R_{m}) H (m, n) - (P_{m + 1} + (n + 1) Q_{m + 1} + (n + 1)^{2} R_{m + 1}) H (m + 1, n) \\ = ((m + n + 2)^{4} (P_{m} + (n + 1) Q_{m} + (n + 1)^{2} R_{m}) - (P_{m + 1} + (n + 1) Q_{m + 1} + (n + 1)^{2} R_{m + 1})) \frac{H (m, n)}{(m + n + 2)^{4}} \end{aligned}

なので

\begin{aligned} (m + n + 2)^{4} (A_{m} + n B_{m} + n^{2} C_{m} + n^{3} D_{m}) - (n + 1)^{4} (A_{m} + (n + 1) B_{m} + (n + 1)^{2} C_{m} + (n + 1)^{3} D_{m}) \\ = & (m + n + 2)^{4} (P_{m} + (n + 1) Q_{m} + (n + 1)^{2} R_{m}) - (P_{m + 1} + (n + 1) Q_{m + 1} + (n + 1)^{2} R_{m + 1}) \end{aligned}

が常に成り立つように $(n + 1)^{r}$ の係数を比較すると

\begin{array}{r} {\begin{cases} [1] (4 M - 3) D = R \\ [2] (4 M - 2) C + (6 M^{2} - 12 M + 3) D = Q + 4 M R \\ [3] (4 M - 1) B + (6 M^{2} - 8 M + 1) C + (4 M^{3} - 18 M^{2} + 12 M - 1) D = P + 4 M Q + 6 M^{2} R \\ [4] 4 M A + (6 M^{2} - 4 M) B + (4 M^{3} - 12 M^{2} - 4 M) C + (M^{4} - 12 M^{3} + 18 M^{2} - 4 M) D = 4 M P + 6 M^{2} Q + 4 M^{3} R \\ [5] 6 M^{2} A + (4 M^{3} - 6 M^{2}) B + (M^{4} - 8 M^{3} + 6 M^{2}) C - (3 M^{4} - 12 M^{3} + 6 M^{2}) D = 6 M^{2} P + 4 M^{3} Q + M^{4} R - R^{'} \\ [6] 4 M^{3} A + (M^{4} - 4 M^{3}) B - (2 M^{4} - 4 M^{3}) C + (3 M^{4} - 4 M^{3}) D = 4 M^{3} P + M^{4} Q - Q^{'} \\ [7] M^{4} (A - B + C - D) = M^{4} P - P^{'} \end{cases} \end{array}

ただし，簡潔の為 $X_{m} := X, X_{m + 1} := X^{'}, M := m + 1$ としています。 $F, G$ での $n$ の次数は，変数の個数と連立する漸化式の個数が一致するように調整しています。
これらを少し丁寧に解いていきます。まず， $[1]$ と $[2]$ から $R$ を消去すると

\begin{array}{r} [2^{'}] Q = (4 M - 2) C - (10 M^{2} - 3) D \end{array}

を得ます。 $[1], [2^{'}]$ を $[3]$ に代入すると

\begin{array}{r} [3^{'}] P = (4 M - 1) B - (10 M^{2} - 1) C + (20 M^{3} - 1) D \end{array}

を得ます。 $[4]$ の両辺を $M$ で割ったものに $[1], [2^{'}], [3^{'}]$ を代入すると

\begin{array}{r} [4^{'}] 4 A = 10 M B - 20 M^{2} C + 35 M^{3} D \end{array}

を得ます。 $[1], [2^{'}], [3^{'}], [4^{'}]$ を $[5]$ に代入すると

\begin{array}{r} [5^{'}] 2 (4 M + 1) D^{'} = 10 M^{3} B - 30 M^{4} C + 63 M^{5} D \end{array}

を得ます。 $[1], [2^{'}], [3^{'}], [4^{'}]$ を $[6]$ に代入すると

\begin{array}{r} [6^{'}] 2 (4 M + 2) C^{'} - 2 (10 M^{2} + 20 M + 7) D^{'} = 10 M^{4} B - 32 M^{5} C + 70 M^{6} D \end{array}

を得ます。 $M \times [5^{'}] - [6^{'}]$ より

\begin{array}{r} [8] 2 C^{'} - 7 (M + 1) D^{'} = - \frac{M^{5}}{2 (2 M + 1)} (2 C - 7 M D) \end{array}

これと， $[2^{'}]$ より $Q_{0} = 2 C_{0} - 7 D_{0}$ となることから

\begin{array}{r} [8^{'}] 2 C - 7 M D = \frac{(- 1)^{m} m!^{6}}{(2 m + 1)!} Q_{0} \end{array}

を得ます。 $[8^{'}]$ と $[5^{'}]$ から $C$ を消去すると

\begin{array}{r} [9] B = \frac{21}{5} M^{2} D + \frac{4 M + 1}{5 M^{3}} D^{'} + \frac{3}{2} \frac{(- 1)^{m} m!^{6} M}{(2 m + 1)!} Q_{0} \end{array}

を得ます。 $[4^{'}], [8^{'}], [9]$ から $A$ を $D$ で表すと

\begin{array}{r} [10] A = \frac{7}{4} M^{3} D + \frac{4 M + 1}{2 M^{2}} D^{'} + \frac{5}{4} \frac{(- 1)^{m} m!^{6} M^{2}}{(2 m + 1)!} Q_{0} \end{array}

を得ます。これで， $A, B, C, P, Q$ を $D$ で表すことができました。
すなわち

\begin{aligned} A = \frac{7}{4} M^{3} D + \frac{4 M + 1}{2 M^{2}} D^{'} + \frac{5}{4} M^{2} V \\ B = \frac{21}{5} M^{2} D + \frac{4 M + 1}{5 M^{3}} D^{'} + \frac{3}{2} M V \\ C = \frac{7}{2} M D + \frac{1}{2} V \\ P = - \frac{1}{10} (182 M^{3} - 158 M^{2} - 35 M + 10) D + \frac{16 M^{2} - 1}{5 M^{3}} D^{'} + \frac{1}{2} (2 M - 1) (M - 1) V \\ Q = (4 M - 3) (M - 1) D + (2 M - 1) V \\ R = (4 M - 3) D \end{aligned}

となります。ただし簡潔の為 $V = \frac{(- 1)^{m} m!^{6}}{(2 m + 1)!} Q_{0}$ としています。
$D$ の初期条件をみます。上式から

\begin{aligned} D_{0} = R_{0} \\ D_{1} = \frac{1}{3} P_{0} - \frac{1}{30} D_{0} \end{aligned}

がわかります。また， $D_{0}$ と $D_{1}$ が決まれば $A$ ～ $R$ がすべて決まることがわかります。これらの $A$ ～ $R$ を $D$ で表したものを $[7]$ に代入することで三項間漸化式が現れます。この漸化式の一般項の明示式を求めるのは非常に困難であると予想します。
となれば $D$ が常に $0$ となればうれしいです。そのために $R_{0} = P_{0} = 0$ とします。また， $Q_{0} = 1$ とします。
これにより， $D$ は常に $0$ となり

\begin{aligned} A = \frac{5}{4} M^{2} V \\ B = \frac{3}{2} M V \\ C = \frac{1}{2} V \\ D = 0 \\ P = \frac{1}{2} (2 M - 1) (M - 1) V \\ Q = (2 M - 1) V \\ R = 0 \end{aligned}

となります。これらを $F, G$ に代入すると

\begin{aligned} F (m, n) = \frac{5 (m + 1)^{2} + 6 (m + 1) n + 2 n^{2}}{4} \frac{(- 1)^{m} m!^{6}}{(2 m + 1)!} {(\frac{n!}{(m + n + 1)!})}^{4} \\ G (m, n) = \frac{m + 2 n + 2}{2} \frac{(- 1)^{m} m!^{6}}{(2 m)!} {(\frac{n!}{(m + n + 1)!})}^{4} \end{aligned}

となります。ペアが求まれば，あとは代入するだけです。
すなわち

\begin{array}{r} \sum_{m = 0}^{\infty} F (m, 0) = \sum_{n = 0}^{\infty} (F (n, n) + G (n + 1, n)) \end{array}

より

\begin{array}{r} ζ (3) = \frac{1}{2} \sum_{n = 1}^{\infty} \frac{(- 1)^{n - 1} (205 n^{2} - 160 n + 32)}{n^{5} {(\binom{2 n}{n})}^{5}} \end{array}

を得ます。

投稿日：2021年12月30日

この記事を高評価した人

高評価したユーザはいません

この記事に送られたバッジ

バッジはありません。

バッチを贈って投稿者を応援しよう

バッチを贈ると投稿者に現金やAmazonのギフトカードが還元されます。

投稿者

＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿

280

17615

他の人のコメント

コメントはありません。

読み込み中

＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿

𝐖𝐙 𝐦𝐞𝐭𝐡𝐨𝐝 覚書

$𝐓 𝐡 𝐞 𝐖 𝐙 𝐦 𝐞 𝐭 𝐡 𝐨 𝐝$
$B i n o m i a l t h e o r e m$
$S h a d o w i n g$
$T h r e e P a t h s W a y 1$
$T h r e e P a t h s W a y 2$
$t e l e s c o p i n g s u m$
$Markov-WZ m e t h o d$
$p a r a m e t e r i z e d$
$a c c e l e r a t e d s e r i e s f o r ζ (3)$

𝐖𝐙 𝐦𝐞𝐭𝐡𝐨𝐝 覚書

𝐓𝐡𝐞 𝐖𝐙 𝐦𝐞𝐭𝐡𝐨𝐝

Binomial theorem

Shadowing

Three Paths Way 1

Three Paths Way 2

telescoping sum

Markov-WZ method

parameterized

accelerated series for ζ(3)

この記事を高評価した人

この記事に送られたバッジ

投稿者

コメント

他の人のコメント

$𝐓 𝐡 𝐞 𝐖 𝐙 𝐦 𝐞 𝐭 𝐡 𝐨 𝐝$

$B i n o m i a l t h e o r e m$

$S h a d o w i n g$

$T h r e e P a t h s W a y 1$

$T h r e e P a t h s W a y 2$

$t e l e s c o p i n g s u m$

$Markov-WZ m e t h o d$

$p a r a m e t e r i z e d$

$a c c e l e r a t e d s e r i e s f o r ζ (3)$